初中数学教学中数形结合的教学案例探讨

邹嫚嫚

(南京市第一中学初中部，江苏南京，210000)

数形结合可以将课本中复杂的数字及文本联系起来构建成有形体，更利于学生理解数学、思考数学.初中数学是小学数学到高中数学的一道分水岭，起到承上启下的作用.初中之后数学方面的抽象部分会越来越多，又因为有些学生还停留在小学的思维方式上，一时间无法理解初中数学的奥妙.以至于整个初中数学都处于懵懵的状态，到了高中甚至连课都听不明白.所以为了高中学数学不吃力，初中数学必须打好基础.而数形结合能够有利于让学生较为轻松地完成任务，并且以数形结合的原理为学生打下坚实的基础，锻炼学生的思维能力和逻辑能力，让学生能够更加高效地完成数学任务，促使初中数学学习质量全面提升.

1 初中数学教学存在的主要问题

1.1 缺乏思维引领

初中数学处于基础课程阶段，会在一定程度上影响到高中甚至大学的数学学习.数学不仅要让学生学会知识和运用知识，还应更深层次的锻炼思维能力.初中数学所要发展的就是想让学生在思维能力上更上一层楼，但是现阶段许多教师只注重学生是否会解题，淡化理解数学知识的本质.导致学生无法在思维上有所突破，以至于学生整体的数学水平也没有提升，这样会距离教学目标越来越远.所以教师需要有所改变不应该片面的停留在只注重学生是否解得出来上，要具有引导意识，让学生的思维能力更上一层楼.

1.2 忽略学生是否真正掌握与理解

在多年的教研活动中，教师们一直注重的就是教，让学生准确掌握知识以及正确的理解却忽略了.数学需要理解透彻才能长久地记住，但是现在学生所表现的是学进去只有短暂地记忆.应当引导学生准确的理解，且不断的回忆.而数形结合教学模式就是一直在强调学，学得透彻学得准确，可以大大地提高数学教学质量，且能够保证每位学生都能准确理解数学的知识点和解题思路等.

2 数形结合在数学教学中的重要意义

在传统的教学模式中教师一般要求学生按模板解题以至于一直无法突破，并且学生只能死板的按照传统的方法解题，导致学生认为学习是枯燥乏味的.但是数形结合的教学是要求学生懂得从不同角度解题以及按照自己的思维去解题.不断提升学生自身的思维能力，增强兴趣值，让数学更有趣.时代在发展，新事物也在随着时代的发展不断诞生.传统的解题思路终将会被淘汰，要用新型的思维去思考教学，不断提高初中数学教学质量，为了实现数学教学质量的基本目标，数形结合教学能够发挥一定的作用.

3 数形结合助解题

3.1 思想概述

一般而言，解决数学问题的方法不止一种，基本上每个题目都有多种模式，而有的模式有时不仅让学生无法理解甚至还会让学生对该题所涉及到的知识点晕头转向，让学生更加无法理解数学.而数形结合的出现是利用题目的数量关系与现实的空间模式相互转化且相互联系，让模糊不清的数式变成具象的图形，再将转换的具象图形与抽象的数式相串联，且利用题目所设定的条件，将题目转化为通俗易懂的图形，这样充分利用了学生的思维能力，使得在解题方面的能力更加绰绰有余.

(1) 以形助数:仔细观察图形的形状、大小、位置关系，充分利用线段、面积与周长等数量关系将数转化为形来求解.

(2) 以数解形:要先充分挖掘出图形中的数量关系，使用代数式求解几何问题，根据图形建立方程或函数关系是常用的方法.

3.2 例析数形结合的使用方法

例1如图1，大长方形的面积从整体看：S=m(a+b+c),同时大长方形的面积也可以从局部表示成:S=S1+S2+S3=ma+mb+mc.

于是有m(a+b+c)=ma+mb+mc.

如图2，大长方形的面积从整体可以表示成(a+b)(m+n).

图1

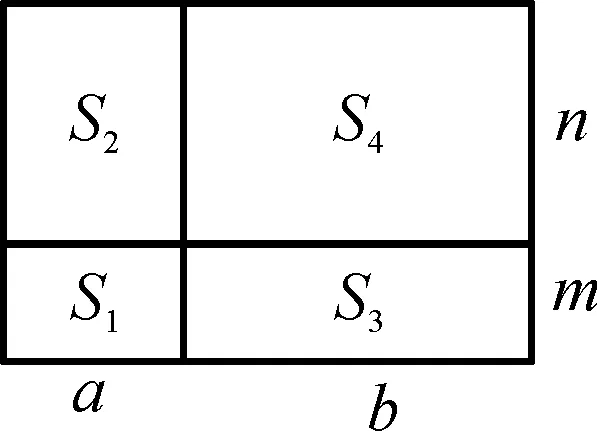
图2

同时这个大长方形的面积也可以从局部表示成S=S+S2+S3+S4=ma+mb+na+nb; 于是有(a+b) (m+n)=ma+mb+na+nb.

例2若方程lg(-x2+3x-m)=lg(3-x)在x∈(0，3)内有唯一解，求实数m的取值范围.

解：原方程变形为y=-x2+3x-m=3-x即：(x-2)2=1-m

图3

设曲线y=3(x-2)2，x∈(0，3)和直线y=1-m，图象如图3所示.由图可知：① 当1-m=0时，有唯一解，m=1；

② 当1≤1-m<4时，有唯一解，即-3

∴m=1或-3

例3已知定义在R上得函数y=f(x)对任意x都满足f(x+2)=f(x),当-1≤x<1时，f(x)=x3，g(x)=f(x)-loga(x)只有四个零点，则a的取值范围是多少?

解:根据已知条件f(x)的周期为4,先画出f(x)一个周期的图象，当-1≤x<3时，f(x-2)=(x-2)2=-f(x)，f(x)=-(x-2)2，由此画出[-1,3)的图象,此为一个周期,图象如下，g(x)=f(x)-loga|x|只有四个零点即f(x)与y=loga|x|只有四个交点，需分类讨论：

(1) 当0

(2)当a>1时，也有两个界值，如下图所示:

此时3个交点，代入(-3，1)，解得a=3，

评注数形结合题型,一定要结合图象分析,并且一些用于定位的特殊点要善于把握;另一方面,必须熟悉初等函数的所有性质及函数图象的变换.

总而言之，数形结合的教学方式值得我们深入探讨.有效地使用不仅能够有效地提高学生学习数学的兴趣和自信心，还可以提高学生学生数学的水平.