解题教学中的“图穷匕见”

缪 雨

(福建省福安市城北中学，福建福安，355000)

根据“双减”政策对于中小学提出了“减轻学生作业负担”的总体要求，中小学学校要完善作业管理办法，统筹从全学科出发，合理调控作业结构，减少作业总量.但对于中学生而言，面临着中考这一“人生分水岭”，又不得不加大加深学习的投入，大量刷题，以应对层出不穷的考题.以数学为例，每年的中考试题都在求新求变中考查学生的“思维能力”，如果学生没有进行重复大量的训练，根本无法在2个小时内完成大部分的试题，更不要说解决多达20分值的填选解答压轴题.

本文将通过“图何来，解何去”这个确定性思想让学生学会通过绘制图形的过程来寻找解题方法.这样既能巩固基础知识，又能有效地思考解决问题的方法，在减少学生作业量的基础上提高学生动手动脑的主观能动性.下面结合初一、初二、初三、中考试题中4道例题的解决方法来谈谈这方面的思考与实践.

1 经构图过程，寻解题思路

例1如图1，将一张长方形的纸片ABCD沿EF折叠，CE交AF于点G，过点G作GH∥EF，交线段BE于点H.说明GH平分∠AGE．

图1-1

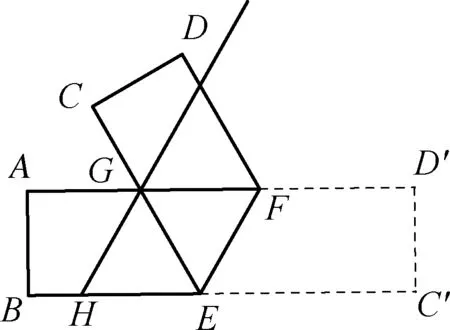
图1-2

例题分析：本题若在图1-1中解决问题，那么为了判断GH平分∠AGE而进行角的推导时会发现无法运用到题目中最重要的条件—折叠，这时只需补齐翻折前的部分，如图1-2由AD′∥BC′可得∠AGE=∠C′EG，再由EF平分∠C′EG、GH∥EF，即可说明GH平分∠AGE，问题得解.

就学生的视界与正常的思维方式，必定只着眼于图1-1中的角进行推导.因此在教学中应要求学生思考：图1-1是如何得到的，翻折前四边形CDFE的位置在哪？此时学生画出四边形C′D′FE后必能根据图形直观通过翻折的性质发现EF平分∠C′EG，进而解决问题.

根据确定性思想，当我们解决一些复杂的问题时，关键就是要寻找确定这个问题的所有条件.它们往往就是能不能顺利解决问题的突破口.这是解题、审题的一种重要思考方式及策略.也就是所谓的解题意识，只有先树立了这样的解题意识，才能谈解题能力的提升与积累.然而笔者以为只通过读题学生不容易发现决定问题的所有对应条件，而让学生通过题目重新绘制图形不但能找到这些条件，而且能察觉题中隐含的信息，让辅助线的生成变得必然且自然.

例2已知四边形ABCD形状如图2-1所示，其中∠A=60°，AB⊥BC，AD⊥CD，AB=2，CD=1，求AD、BC的长．

图2-1

图2-2

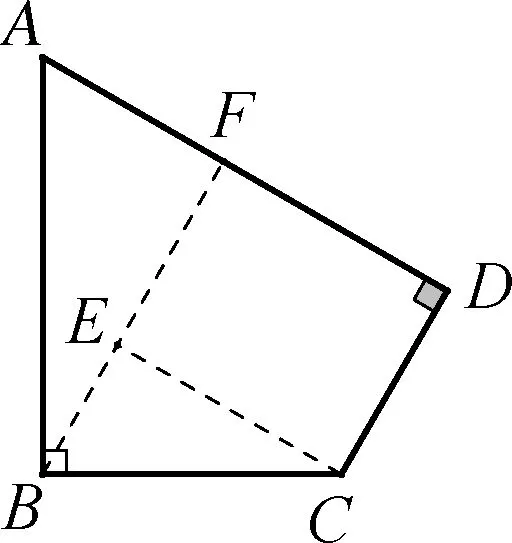
图2-3

例题分析：本题通过确定性思想可以有多种解法，例如图2-2和图2-3中构造一线三直角来确定图形点、线、角的位置可以很快解决问题.

图2-4

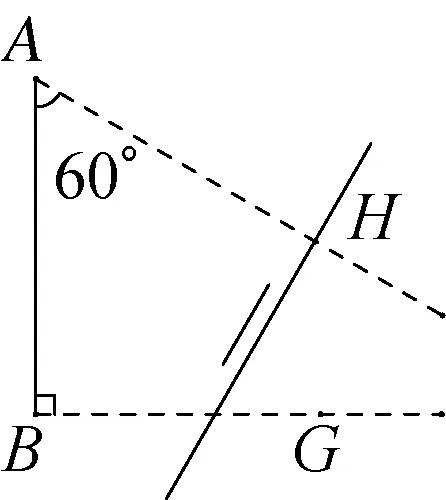
图2-5

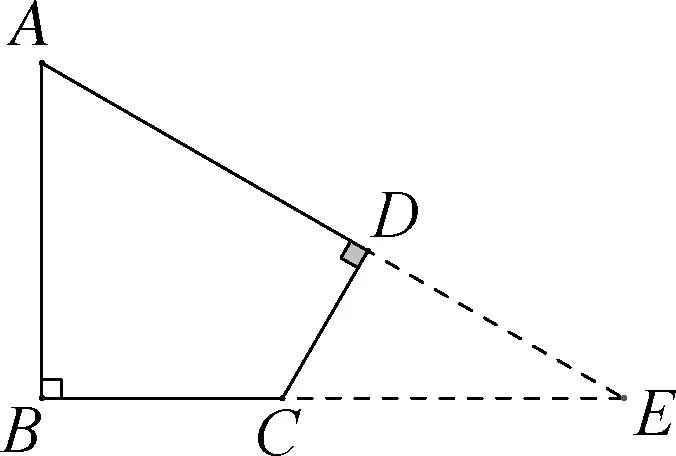
图2-6

但这些方法对学生分析条件运用模型的能力提出较高的要求.笔者认为延长AD、BC构造出Rt△ABE是最本质的解法，然而如何让学生能够想得到呢？这里只要让学生绘制出符合条件的四边形ABCD，学生必然有了构造△ABE的意识.首先由于AB的长和∠A、∠B的度数是确定的，因此能画出来的部分如图2-4所示.接下来因为CD的长度是确定的且要求CD垂直于AH，那么我们可以如图2-5所示让三角板一直角边与AH重合，让三角板沿AH方向平移，直到三角板另一直角边在射线AH、BG间的线段长度符合CD的长时停止平移，则此时CD的位置也就确定，四边形ABCD也就绘制完成.以上构图过程中不论是如图 2-4中的画射线AH、BG，还是如图2-5中的平移三角板，都让学生感受到让射线AH、BG继续延展的自然过程，到这里必然会画出如图2-6的Rt△ABE，回到了学生最熟悉解三角形部分.让学生深刻感受到一个确定的元素是如何确定下来的，就是怎么求解的思想.

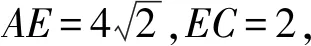
图3-1

例题分析：本题∠BAC是确定的，AE、EC的长度也是确定的，因此可以绘制如图3-2.因为点F是△ABC的外心，则DE⊥AB于点D，且D是AB中点，所以可以依次确定点D与点B的位置，进而确定AB的长度，绘制出△ABC如图3-3.点E的位置是确定的，求EF长的关键是确定点F的位置，而点F是△ABC的外心，那就必需再绘制△ABC的边AC或BC的垂直平分线，与DE的交点就是点F.因为AC的长度是确定的，所以AC的垂直平分线也是确定的，与DE的交点F也就确定了，则EF必可求.通过重新绘制本题的图形，坚定了学生解决问题的信心，更重要的是让隐藏起来的线FG必然的显现出来，使添加辅助线变的自然而然.

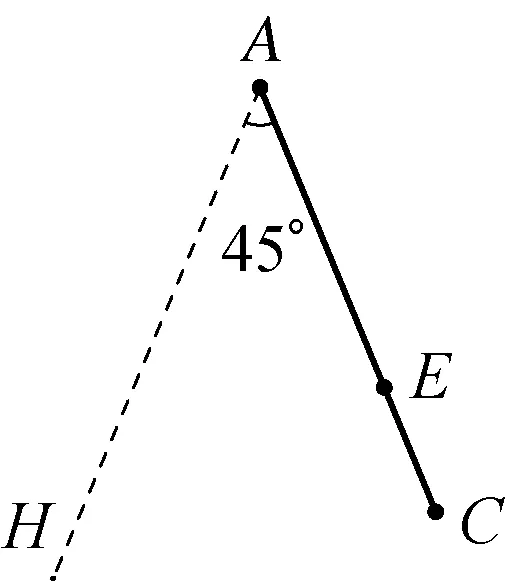
图3-2

图3-3

图3-4

在初中三年的教学中，一种好的思维方式只教学生一次是不够的，需要教师在不同的阶让学生反复经历.“反复经历、深化认识”，既是对学生不同学习阶段的客观要求，也是促进学生积累经验、提升解题能力的必经之路.

通过以上这3道例题，让学生分阶段感受当解题遇到困难时，经历回溯图形的绘制过程，分解或组合条件思考能得到什么，即分析确定的量与确定的关系，将所知与问题相结合，发现隐藏的信息，找寻解题思路.

一个问题有多种解法固然能提高思维的广度，但多个问题归于一种解法更为重要，这不仅减少学生的课业量更是有效提高学生的思维的高度，达到“解一题，会一类，通一片”.

2 多视角回溯绘图，究解题方法

一些经过大量刷题训练的学生确实“见多识广”,但是他们对概念、定理定律和公式法则这些抽象的东西没有深入琢磨和思考，造成抽象思维很难建立起来.特别的，这些学生只是机械的记忆一些解题技巧和方法，却缺失了分析、思考问题的能力.

图4-1

图4-2

图4-3

这些学生通过模仿费马点问题构造旋转或许能解决问题，但其中构造什么、怎样构造、为什么要构造不甚了了，特别是解题时必然会遗漏本题的多种结论.接下来对本题通过回溯图形的绘制过程进行定性分析

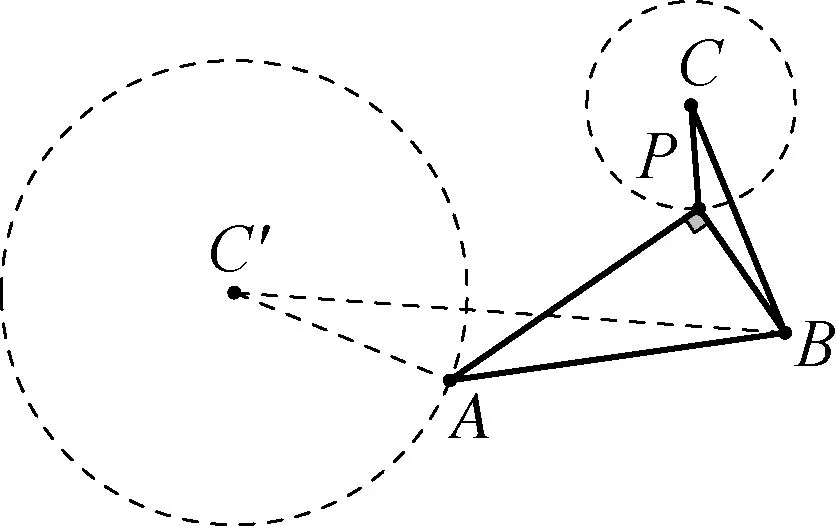
图4-4

如图4-5，绘制∠BCD=∠ABP，由 tan∠ABP=tan∠ACB=2，即点A在射线CD上.

图4-5

图4-6

综合点A即在⊙C′上又在射线CD上，可得点A为⊙C′与射线CD的交点.

由图象发现圆与射线有2个交点，说明本题满足条件的AC的长有2个.当然由于学生绘制图象不一定准确，但当出现这种情况下肯定会思考直线与圆的位置关系，察觉本题不能只按题目原图解决问题，而要思考是否有不同解.

如图4-6，当图形绘制完成之后自然形成一个常见的旋转变换的几何模型，那么连接CC′，在△ACC′中，CC′、AC′、∠ACC′都是确定的，这是由于“边边角”的条件，因此可得两个AC的值，这也与所绘制的结果相符合.

图4-7

图4-8

图4-9

3 反思“绘图解题”，锻炼深度思维

解题要“瞻前又顾后”，解题后进行反思.简单的题目就琢磨其蕴含的基本图形，难题就想解决这个问题的方法和策略.把握住思想和方法，提炼出对未来解题有指导作用的信息.

反思“回溯图形绘制进行解题”的方法，发现不但对数学题目本身及解题方法的重新认识，而且在绘制图形的过程中看到本题用到哪些知识、什么方法，这些知识与方法是如何组合在一起的，从中巩固概括出的基础知识、逻辑结构等.同时绘制图形直观展现了确定问题源的条件，支持学生平移、旋转、翻折，让图形更生动、学生的思维更深入，更恣意伸展！