定点证明,思维展开,结论推广
——一道解几题的探究
刘 云
(江苏省泰兴中学,江苏泰兴,225400)
1 问题呈现

(1) 求椭圆E的方程;
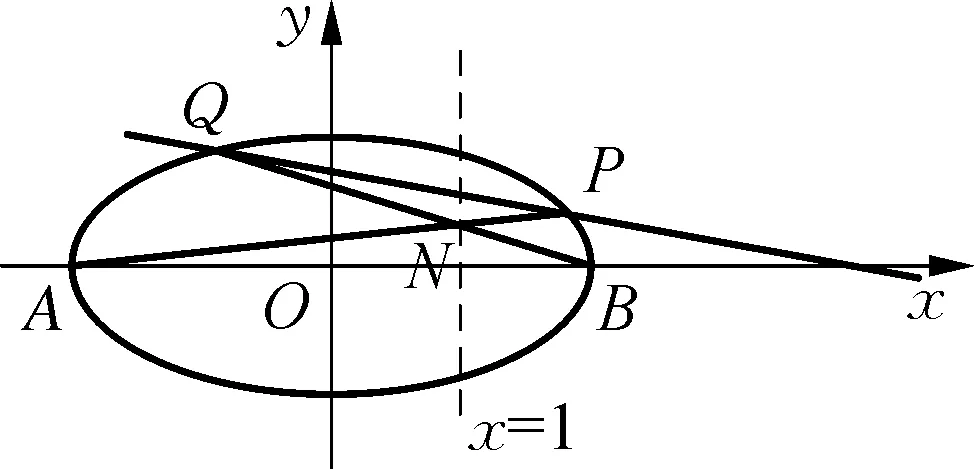
(2) 若N(s,t)是平面上的动点,从下面两个条件中选一个,证明:直线PQ经过定点.

②t=2,s∈R,直线NC,ND与椭圆E的另一交点分别为P,Q.
此题以椭圆为问题背景,第一步求解椭圆的方程,比较常规,起点比较低;第二步以结构不良试题形式来创设问题,根据两个不同方面上的动点与对应两长轴(或两短轴)的端点所对应的两条直线与椭圆的另一个交点,形成一条新直线必经过定点来创设新的题型,在考查学生分析问题、解决问题能力,以及理解能力、探究能力、创新能力与应用意识等的同时,具有很好的开放性与创新性,
2 问题破解



解后反思:根据题目条件求解圆锥曲线的方程,往往是此类问题的第一小步,难度不大.可以依据条件构建方程(组),或借助圆锥曲线的定义合理构建关系式来确定参数a,b,c的值,从而来确定圆锥曲线的方程.这是较为常规的设置,通常采用常规方法.
(2) 选择条件①:



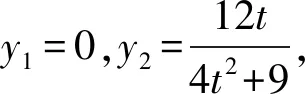

当t=0时,P(2,0),Q(-2,0),直线PQ为x轴;

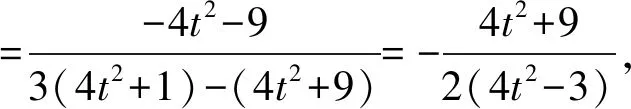

综上所述,直线PQ经过定点(4,0).
解后反思:设线法是解决圆锥曲线中的定点问题时比较常规的一种技巧方法,以直线的方程,与圆锥曲线的联立,沿着常规破解直线与圆锥曲线的位置关系问题的基本思路加以推进,实现问题的解决.设线法思路常规,目标明确,但运算量大.
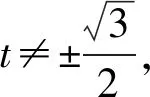
当t=0时,P(2,0),Q(-2,0),直线PQ为x轴,所以直线PQ经过的定点应在x轴上;
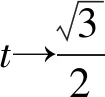
直线PQ经过的定点应是切线l与x轴的交点(4,0).
证明如下:(亦可以通过另一些特殊位置(如取t=1)分析出定点(4,0).)
由(1),不妨设A(-2,0),B(2,0),P(x1,y1),Q(x2,y2),




而动点N的横坐标x=1,所以要证原命题成立,只需证明x=1是上述方程的根,

将x1=my1+4,x2=my2+4代入,只需证明3y1(my2+2)+y2(my1+6)=0,只需证明2my1y2+3(y1+y2)=0,

综上所述,直线PQ经过定点(4,0).
解后反思:先猜后证法吻合圆锥曲线中定点问题破解的基本思维过程,利用思维过程中先确定定点,再加以科学验证的基本思路来展开,体现思路历程.先猜后证法具有推理中分析法的特性,但过程比较繁杂.
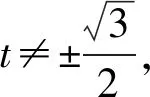
当t=0时,P(2,0),Q(-2,0),直线PQ为x轴,所以直线PQ经过的定点应在x轴上,
不妨设A(-2,0),B(2,0),设P(x1,y1),Q(x2,y2),定点M(m,0),



综上所述,直线PQ经过定点(4,0).
解后反思:共线性质法是合理利用条件中三点共线所对应的直线斜率相等来合理构建对应的关系式,综合圆锥曲线的定义、几何性质等来合理联系,从而实现问题的破解.共线性质法合理利用条件中的众多点、线之间的联系,逻辑推理性强.
而对于条件②,可以类比条件①中的解析方法,同样可以得以有效解决.下面以设线法加以展开.
选择条件②:
解:(设线法)N(s,2),s为变量,由(1),不妨设C(0,-1),D(0,1),
则直线NC的方程为3x-sy-s=0,直线ND的方程为x-sy+s=0,
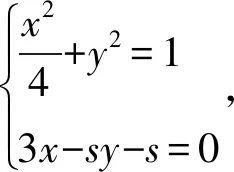
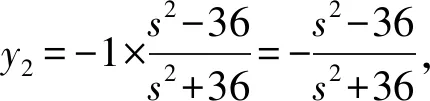
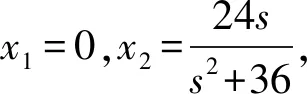

当s=0时,P(0,1),Q(0,-1),直线PQ为y轴;

考虑到椭圆的对称性,令x=0,
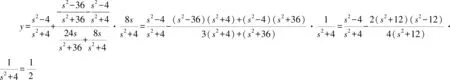

3 结论总结
根据以上具体问题与解析过程,对问题中的条件进一步加以深化、推广与拓展,可以得到更具一般性的结论.


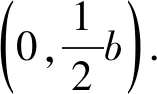
4 教学启示
涉及圆锥曲线中直线过定点问题,破解的基本思维方法有两大类:
(1) “一般推理,特殊求解”,主要是根据题设条件加以合理设参,或设点,或设线等,结合条件构建相应的关系式,进而加以推理、运算,借助消参数或参数的任意性,通过推理或运算得到相应的定点坐标,即可达到目的.
(2) “特殊探路,一般证明”,主要是根据题设条件从特殊情境、特殊位置等场合入手,确定定点坐标,再把问题进行合理转化,朝着已经确定的定点方向,有目标性地推理或运算,“特殊探路”是确定目标,“一般证明”是完备过程,在解答题中两者缺一不可,在选择题或填空题中就可不必去证明.

