GeoGebra辅助教学的可视化实践研究——以2022年的一道高考题为例

王 永，刘菲菲

(1. 安徽省肥西中学，安徽合肥，231200 2. 合肥经济学院，安徽合肥，231200)

1 问题呈现

(1) 求l的斜率；

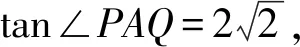
此题凸显核心素养，尤其是数学抽象和数学运算，是一道难得的经典好题.

2 问题解决

GeoGebra简称GGB，是一款功能及其强大的动态可视化数学软件，适用于多种学科.下面先用GGB来解答教学，然后对此进行验证并严格证明.

① 在指令输入框输入方程0.5x2-y2=1；

② 作直线y=1，在双曲线上取一点P，用工具直线(line)连接AP；

③ 用指令Reflect(g,f)作出对称直线交双曲线于Q，用工具直线(line)连接AQ,PQ；

④ 选中工具栏斜率(Slope)分别点击直线AP,AQ,PQ；

⑥ 拖动动点P，可以始终看到kAP+kAQ=0，kPQ=-1.

继续来解答(2)：

① 在指令输入框输入方程0.5x2-y2=1，再输入y=sqrt(2) x-2sqrt(2)+1即AP；

② 指令框输入y=-sqrt(2) x+2sqrt(2)+1即AQ，用工具直线(line)连接PQ，在代数栏可以立刻得到它的直线斜截式方程，并用工具文本(text)输入l_{PQ}：y=-x+frac{5}{3}；

图1和图2分别展示了此题两问的最终结果.

图1

图2

传统教学，老师只能画出草图示意，无法动态展示动点问题，也不能具体展示出题目蕴含更深刻的数学知识，学生难以理解想象，可视化效果弱.使用GGB动态软件，能够使抽象问题具体化，激发了学生的学习兴趣和研究热情，加深了对数学概念的理解，促进学生对现有知识的深思考，重构再加工，从而真正做到对数学知识的融会贯通.

下面对此题给出严格证明：

(1)解法1：设直线PQ的方程为y=kx+m，P(x1,y1)，Q(x2,y2)，于是

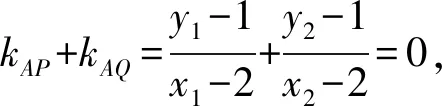
(x2-2)(y1-1)+(x1-2)(y2-1)=0⟹2kx1x2+(m-2k-1)(x1+x2)-4m+4=0，

由于直线AP,AQ的斜率必须存在，即直线l不能经过A点，所以k=-1.

解法2：可设直线AP的方程为y=kx-2k+1(k≠0)，则直线AQ的方程为y=-kx+2k+1.于是

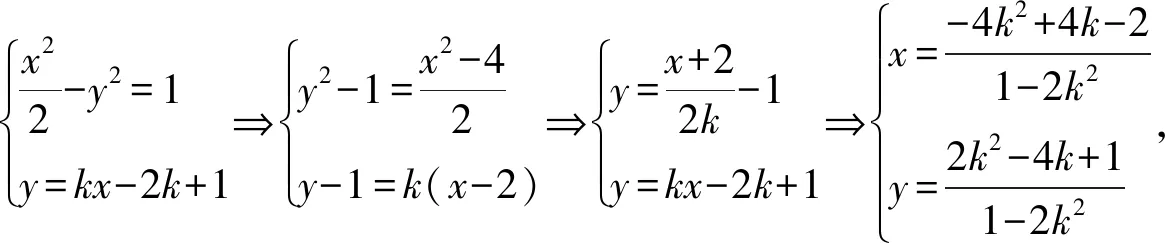
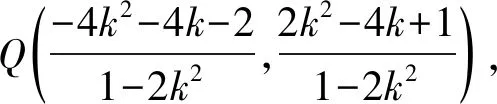
所以，直线l的斜率为-1.

此题也可以用韦达定理解出P的坐标，读者可以自行尝试，在此不再赘述.

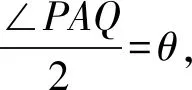
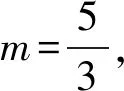
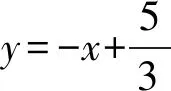
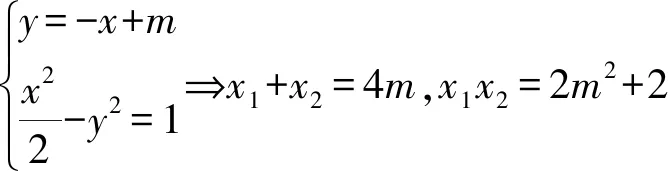
3(x1-2)(x2-2)+3(y1-1)(y2-1)=3|(x1-2)(x2-2)|，

(x1-2)(x2-2)+(y1-1)(y2-1)=-(x1-2)(x2-2)，

得m2-6m+9=-2m2+8m-6，

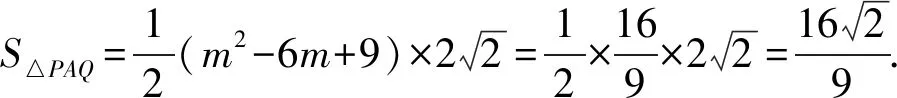
解法3：设直线AP的斜率为k(k≠0)，则直线AQ的斜率为-k，由夹角公式可得

以下同解法1或2，不再赘述.

通过GeoGebra辅助解答教学的可视化实践研究，不难发现，GGB动态课件可以把复杂抽象的数学问题可视化，形象生动，能够激发学生的好奇心和求知欲，从而潜移默化地培养了学生的核心素养；同样GGB软件亦可以让学生轻松实现对本题的推广，譬如可以让学生尝试在椭圆和抛物线中是否也有类似的结论或者其它可能的假设猜想；同时鼓励学生对此题进行简单改编，然后使用GGB进行验证，比如已知S△PAQ的面积求cos∠PAQ等等.