由三视图还原空间几何体——流水线上的“切割”技术

侯杰文，廖 洋

(四川省成都市盐道街中学，四川成都，610000)

由三视图还原空间几何体的过程中，如果把三个方位的空间想象，降低到单方向的空间想象上，可以大大降低空间想象的难度.这就好比是在流水线上对原材料进行“切割”加工，一道接着一道工序，直到产品成型.按照“由易到难，由里向外，重实避虚，三方检验”的原则，可以轻松应对所有三视图还原空间几何体问题.

1 方法展示

例1已知某几何体的三视图如下,请画出该几何体的直观图.

解析：(1) 加工过程，如下图所示

图1

图2

图3

图4

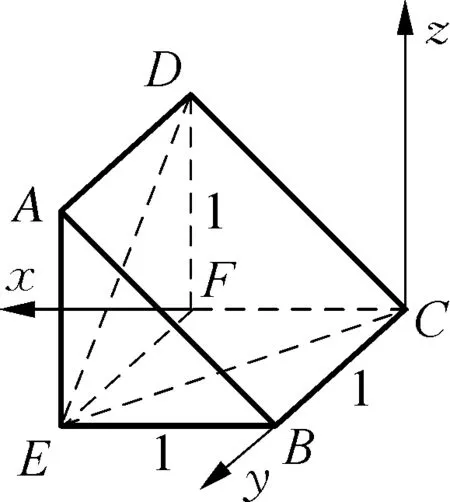
图5

图6

(2) 加工说明

① “由易到难”选原料：观察三个视图的轮廓线，不考虑视图内部的连线，选择正方体作为加工原材料，如图1；

② “由外向里”先外部切割：观察正视图，根据几何体坐标平面xoz的投影，可以做切割平面ABCD，如图2；将右上部分几何体切割掉，所剩几何体为三棱柱ABE-DCF，如图3；

③ “重实避虚”内部精细切割，观察侧视图，根据几何体在坐标平面yoz的投影，由于内部连线是实线(从左往右看是看得见的棱)，因此在几何体左侧面作出且切割线DE；观察俯视图，根据几何体在坐标平面xoy的投影，由于内部连线是虚线(看不见的棱)，因此在几何体底面作出切割线EC，即可得到切割面CDE，如图4.最后将三棱锥D-EFC切割掉，所剩几何体为四棱锥E-ABCD,如图6；

④ “三方检验”做完善：将所剩几何体做三个坐标平面的投影，满足三视图，故切割后的几何体为图6.

变式题已知某几何体的三视图如下,请画出该几何体的直观图.

解析：(1) 加工过程，如下图所示：

图7

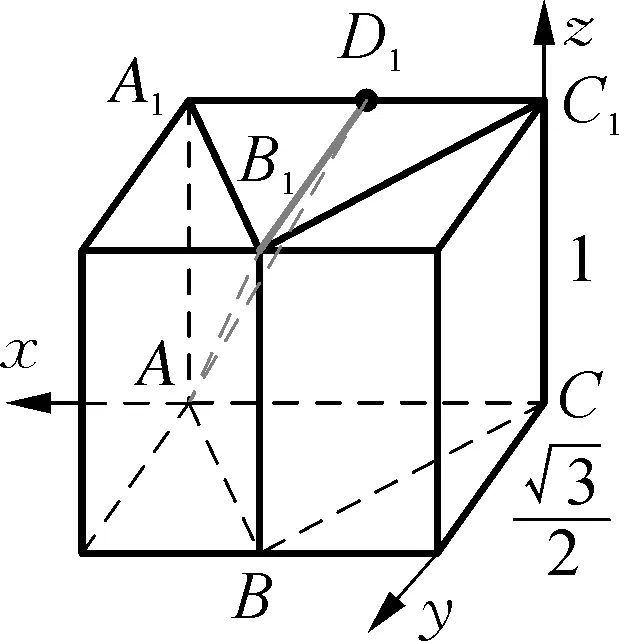
图8

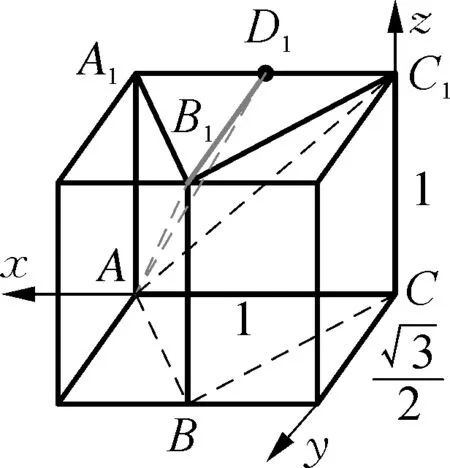
图9

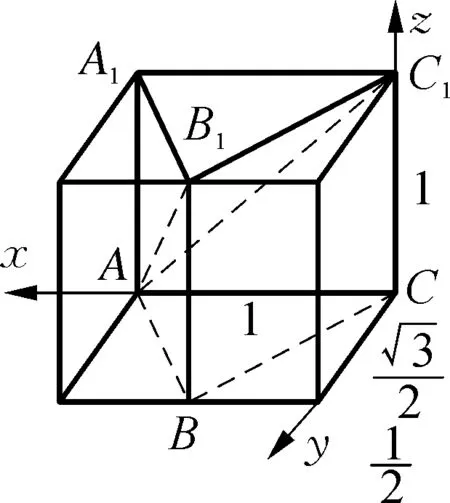
图10

(2) 加工说明

① “由易到难”选原料：观察三个视图的轮廓线，不考虑视图内部的连线，为了增强几何图形的直观，选择长方体作为加工原材料，并做第一步切割，保留几何体三棱柱ABC-A1B1C1，如图7；

② “由外向里”做第二步切割：观察正视图，外围轮廓线是直角梯形，根据几何体坐标平面xoz的投影，可以做切割平面AB1D1(如图8，D1为A1C1中点)，将右上部分三棱锥A-A1B1D1切割掉；

③ “由外向里，重实避虚”做第三步切割，观察侧视图，根据几何体在坐标平面yoz的投影，由于内部连线是实线(从左往右看是看得见的棱)，因此在几何体左侧面恰好是切割线AB1；观察正视图，根据几何体在坐标平面xoz的投影，由于内部连线既有实线也有虚线(看不见的棱)，实线的切割线恰好是BB1，作出虚线的切割线AC1，即可得到切割面AB1C1，如图9.最后将三棱锥B1-AC1D1切割掉，所剩几何体为四棱锥A-BCC1B1,如图10；

④ “三方检验”做完善：利用三视图检验四棱锥A-BCC1B1，符合题意.

例2(2022年全国甲卷第4题)如图，网格纸上绘制的是一个多面体的三视图，网格小正方形的边长为1，则该多面体的体积为( ).

解析：(1) 加工过程，如下图所示：

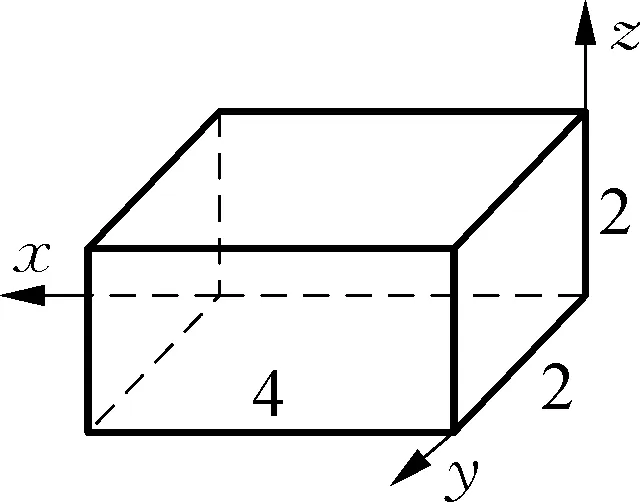
图11

图12

图13

(2) 加工说明

① “由易到难”选原料：从三个视图中首先选择加工原材料，不难发现最简单的视图是侧视图，可以发现利用长方体(长为4，宽为2，高为2)作为加工原材料比较简单.为了增强直观感，将几何体放到空间直角坐标系中，如图11；

② “由外向里”做外部切割：根据正视图在投影面xoz的投影，作出切割平面ABCD,如图12；

③ “由外向里，重实避虚”做精细切割：根据俯视图在投影面yoz的投影，经检验无需再切割，即可得到最终切割后的几何体,如图13；

④ “三方检验”做完善.

(3) 解决问题

例3(2017全国卷2理科第4题)如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为( ).

A． 90π B． 63π C． 42π D． 36π

解：(1) 加工过程

图14

图15

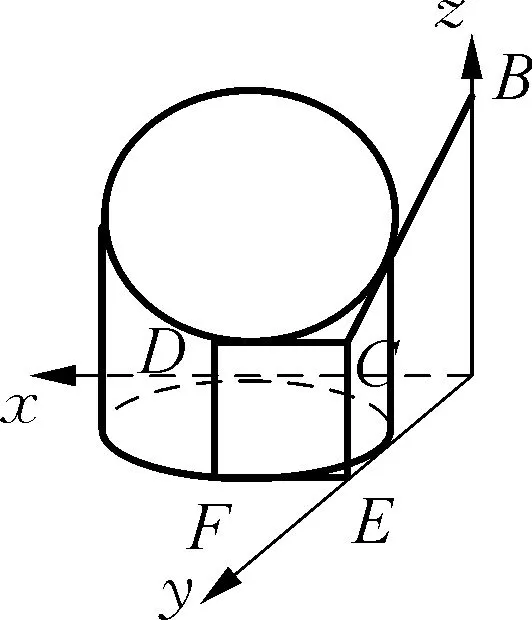
图16

(2) 加工说明

① “由易到难”选原料：从俯视图可以发现利用圆柱作为加工原材料比较简单，如图14；

② “由外向里”做外部切割：根据侧视图视图在投影面yoz平面作出切割线，然后过切割线作切割面ABCD，如图15；

③ “三方检验”做完善：根据正视图验证所作切割面ABCD是否满足题意，同时由三视图确定几何体相关线段长度，不难发现CE=DF=4,底面圆的直径为6.

(3) 解决问题

故该组合体的体积V=V1+V2=36π+27π=63π．故选B．

2 归纳总结

三视图还原空间几何体的流水线上的“切割”步骤：

(1) “由易到难”选原料：一般从简单视图入手，选择简单空间几何体作为加工原材料.如：直棱柱、正棱锥、圆锥、球等简单几何体或简单几何体的组合体；

(2) 选择加工“机床”，增强直观感：一般将空间直角坐标系，长方体、正方体作为加工“机床”；

(3) “由外向里，重实避虚”做切割：选择较简单的视图入手，首先在投影面上确定“切割线”，然后过“切割线”作出切割面；

(4) “三方检验”做完善：检查切割后的几何体是否满足三视图.

3 方法提炼

总而言之，在处理三视图还原空间几何体的问题中，首先是利用简单几何体的模型建构空间几何体，若遇到较复杂的三视图，则可以尝试利用本文中提到的流水线加工策略.

流水线上的“切割”策略本质是：将三个方位的空间想象，分步聚焦到一个方位的空间想象，将发散式思维模式转化为线性思维模式，从而聚焦了思维能量，步步为营，直到成功还原空间几何体.这种方法与策略也体现了转化与化归的数学思想，为聚焦空间想象力、培养学生直观想象的数学核心素养提供了方法与策略.