一道线段比最值问题的解法探究与变式拓展

黄 维

(江苏省宝应县城北初级中学,225800)

最值问题是中考考查的重点,也是考生的难点,并多以填空题、解答题或探究题等形式出现.本文以一道线段比最值问题为例,着力一题多解,以此来培养学生的创新能力,拓宽学生的思维路径.

一、原题呈现

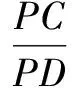
分析本题以正方形为背景,将勾股定理、相似三角形、手拉手模型融为一体,涉及的知识点多,综合性强.

二、多彩解法

解法1(旋转法)如图2,将∆DCP绕点C逆时针旋转90°得到∆BCP′,取边CP的中点E,连结BE,P′E.

由三角形法的三边关系,得

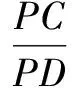
点评由三线共点且有一组线段相等想到旋转,建立手拉手模型,再固定一条边的长,通过三角形的三边关系以确定另一条边的范围,从而求得最值.

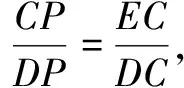
由∆DCE∽∆DPC,可知AD2=CD2=DE·DP.

∵∠ADE=∠PDA,∴∆ADE∽∆PDA,

∴∠AED=∠PAD=90°,

即点E在以AD为直径的圆上.

点评利用相似将双动边比值转化为一动边比一定边,从而转化为定点C到动点E的最小值.而动点E的运动轨迹是以AD为直径的圆,最终通过“一箭穿心”模型解决问题.

解法3(代数法)设BP=x,DC=1,则PC2=x2+1,PD=(x+1)2+1,

(t-1)x2+2tx+2t-1=0.

(*)

∵P是AB延长线上一点,∴t≠1.

点评几何问题直接求解往往比较困难,若采用代数法,有时可取得意想不到的效果.

通过多彩解法的展示,一方面可以通过不同思路的训练,复习了相关的基础知识,感受几何题的殊途同归;另一方面,上述思路方法也可应用到一般问题上.

四、变式拓展

解法1如图5,将∆BCP绕点C顺时针旋转60°得到∆ACP′,取CP的中点E,连结AE,P′E,P′P.

设CP=CP′=a，则由三角形的三边关系,得PB=P′A≤P′E+AE,且当P′,A,E三点共线时,P′A取得最大值.

由∆CDB∽∆PCB,得AB2=BC2=BD·BP.

∵∠ABD=∠PBA,∴∆ADB∽∆PAB,

∴∠ADB=∠PAB=120°,即点D在以AB为弦,所张角为120°的圆弧上.

解法3如图6,过点P作PH⊥BC交BC延长线于点H.

在实际教学中,教者要善于运用“一题多解”,培养学生的求同和求异思维.通过一题多解的训练,不仅开阔学生的视野,而且达到拓宽学生的思维广度,以及锻炼学生的发散思维的目的.