基于改进PSO算法的天线优化联合仿真技术

崔若愚，牛调明，梅中磊

(兰州大学 信息科学与工程学院，甘肃 兰州 730000)

0 引言

传统的天线设计及优化是采用计算机的微波EDA(Electronic Design Automation)仿真软件进行的，多是采用数值求解的方法精确计算和分析电磁特性[1-2]，计算量大、计算时间长，且没有一个高效率的参数优化方法，科研人员利用自己的专业知识和经验来确定等效场路模型，并通过全局优化的形式对天线进行参数更新与选择[3]。如果天线的模型过于复杂，很难用公式及理论对其尺寸和电磁特性的关系进行推导。近些年，得益于机器学习的飞速发展，不少学者逐渐将机器学习相关的最优化算法与天线优化设计相结合,形成了各有优势的参数优化方式[4]。其中，粒子群(Particle Swarm Optimization，PSO)算法[5]因为参数简单、更加符合社会行为的特性被广泛应用于求解连续优化问题中[6]。一些研究表明，在天线设计过程中，使用PSO算法优化天线，能够显著降低计算机全波仿真软件的计算次数，极大地提升天线设计的效率[7-9]。现有的天线联合仿真主要依靠Matlab工具箱与VBS脚本搭配使用，对软件的版本依赖较高，可移植性不强，底层效率不高，而Python作为一种广泛应用于工程领域的脚本语言，具有高效的底层数据结构和程序移植性。

本文主要研究了一种带修正系数的改进型的适应度值预测粒子群(Fitness Estimate Particle Swarm Optimization，FEPSO)算法，并对比了基于研究算法与基于传统PSO算法的联合仿真技术在天线优化中的运用。算法侧重于提升天线优化的效率，因此选择了一种经典的微带八木天线进行优化与验证。与基于传统PSO算法的联合仿真相比，所提算法有较大的效率提升，对其他天线中的尺寸结构优化也具有普适性与工程实践意义。例如，在对某些不规则形状的复杂天线进行设计时，由于缺少人工经验无法推导天线的尺寸参数，而且使用纯粹的软件仿真又会消耗大量的时间，此时使用FEPSO算法，只需要给出尺寸范围和算法参数设置，就可以节省科研人员的精力与时间来自动化地进行寻优。这种联合仿真并不依赖于天线的具体形状和结构，同样可以运用于分型结构天线、超表面天线及阵列天线相位控制等其他器件的设计当中。这种预测方法通过前代的粒子行为与信息对粒子的适应度值进行预测，对于其他领域中的具有昂贵的适应度值计算代价的优化问题也具有借鉴意义。

1 微带八木天线的基本理论

微带八木天线结构如图1所示。微带八木天线以微带天线为基础，介质板正面是通过微带线与馈线相连的有源振子的一臂，另一臂则反方向地印制在介质板的底面。贴片排布用八木天线的形态排列得到。此微带八木天线由激励振子、引向振子和反射振子组成。对天线性能影响较大的参数均已在图中标出，L和W分别对应介质板的长和宽,dr为激励振子的长度,d1为引向振子的长度，W1和W2为激励振子和引向振子的宽度，ɡ1为激励端到激励振子的间距，ɡ2为激励振子与引向振子的间距，ɡ3为引向振子之间的距离。

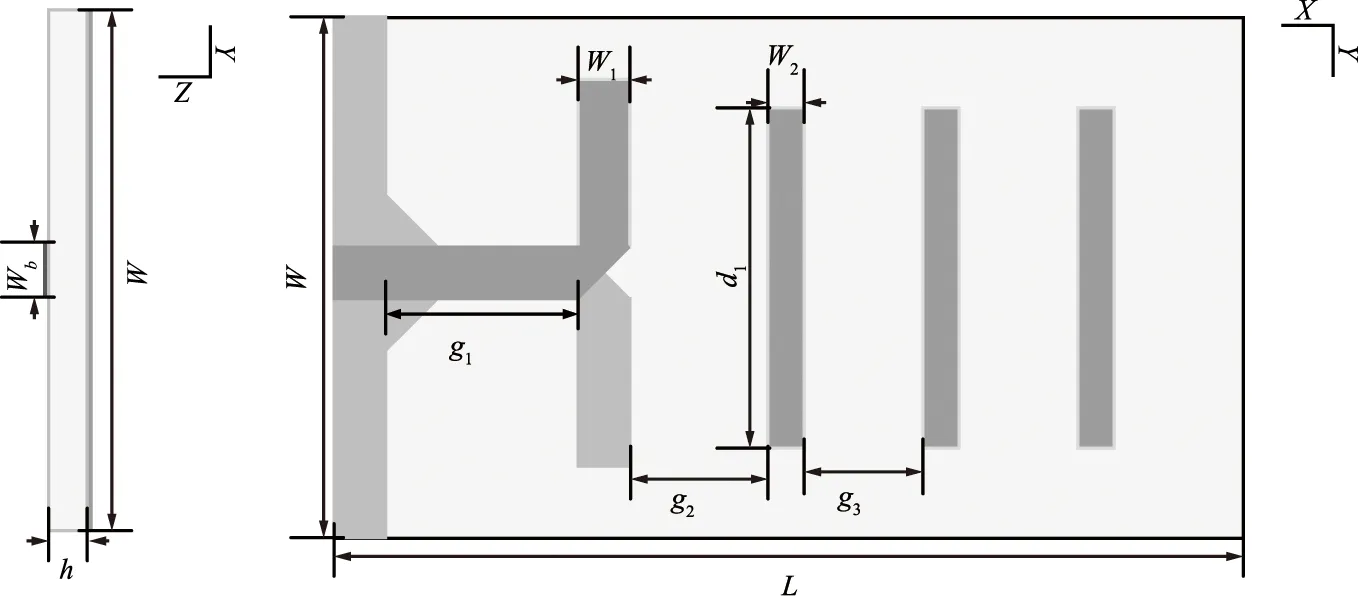
图1 微带八木天线结构Fig.1 Microstrip Yagi-antenna structure

文献[10]介绍了经典微带八木天线的经验公式并进行了天线设计，这也是常用的天线分析与综合的流程，一般步骤是：

① 根据设计要求，先确定所需天线的工作频率、形状、材料以及磁导率等具体数值；

② 通过已知天线的用途及特性，确定所设计天线的具体类型；

③ 查经验公式，通过计算得到目标天线的各项参数；

④ 利用HFSS或者CST等微波EDA软件进行仿真；

⑤ 根据仿真结果人为地进行参数微调，最终得到设计目标天线。

然而，一些经典天线的经验公式对于一些复杂拓扑形状的天线不具有指导意义。在一些对于经典天线的开槽、弯折和加寄生贴片等改进中也已经不能起到辅助设计的作用。本文介绍了一种基于PSO算法进行Python-HFSS天线联合仿真的方法，提出了一种天线综合和分析的新途径，以满足复杂拓扑结构天线的设计与分析，并在天线设计效率上有较大提高。

2 PSO算法逻辑及优化参数选择

在天线建立模型无误后，脚本录制的位置如图2所示，通过Tools→Record Script to File，选择脚本文件存储位置开始进行脚本的录制，它可以将用户点击按钮之后对于模型、参数和设置等操作记录下来。当设置参数的操作完成后，在同样位置点击Tools→Stop Script Recording，会终止录制操作，最终将生成一个py后缀的脚本文件，通过VSCode编译器运行此文件，即可在Python中自动复现刚才进行的所有操作。

图2 脚本录制的位置Fig.2 Script recording position

本文采用的是HFSS 2020(R2)版本，Python则使用VSCode为编译器的Python3.7版本。相比于Matlab，Python是一种更轻量化的脚本语言，在HFSS 16之后就已经开始支持Python脚本的录制功能，具有更为高效的底层数据结构以及工程应用场景，适用于大批量数据的分析处理[11]。PSO算法的一般公式是：

(1)

(2)

式(1)和式(2)分别称为速度更新公式和位置更新公式。式中，i为粒子的数目；d为粒子的维数；k为当前迭代次数；v，x为粒子的速度和位置；pbest为此粒子本身能得到的最优解，称之为个体极值；ɡbest为整个种群目前能找到的最优解，称为全局极值。当选择PSO算法模型的影响系数时，需要对3个变量进行设置，分别是ω，c1，c2(惯性权重与学习因子)。

选择图1给出的天线作为优化目标天线，依据文献[12]，选择的惯性权重ω为0.729 8，学习因子c1=c2=1.496 18。天线的基板采用常用的FR4材料，其介电常数为4.4。粒子x的维度数d即想要优化天线参数的个数。选择dr，ɡ1，ɡ2三个参数作为参数优化的目标，将3个参数组成的粒子作为待优化的搜索粒子，2.5 GHz处的S11参数作为优化的目标，优化逻辑为2.5 GHz处的S11参数越低，越符合最优解。式(3)给出了适应度值fitness的选择逻辑:

fitness=min(S11(fi))，i=0,1，…，NP，

(3)

式中，NP为种群规模；S11(fi)为规定频率处的S11值。

这3个参数的范围以及其他参数的值如表1所示。值得一提的是，本文的算法在初始化过程中，为了在尽可能小的PSO情况下取到具有代表性的点，采用了正交法测试 (Orthogonal Arrays Testing Strategy,OATS)作为初始化种群的优化方式[13]，这种方式相比于传统的随机均匀分布能够取得更有标志性的点，且相比于全组合的笛卡尔积能够节省粒子的数目。采用的生成正交表形式为L16(43)，即生成了16个粒子，3个参数代表了3个因素数，每个因素数的水平均为4，为了避免PSO飞出方向向边界收敛，将初始化的点有意避开了边界值。其水平划分为dr(24,28,32,36),ɡ1(12,14,16,18),ɡ2(12,14,16,18)。正交表可以通过因素数与水平数查表得到，具体生成表因篇幅有限，本文不再赘述。

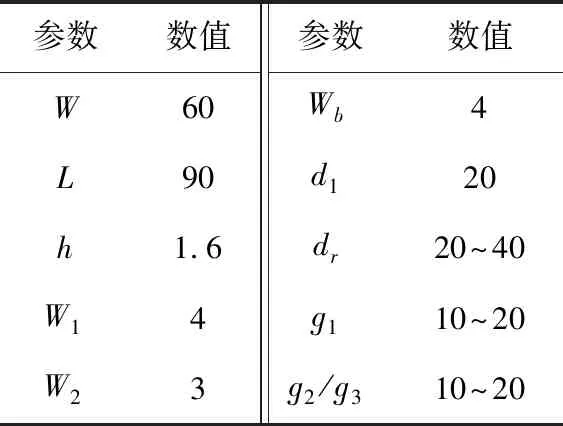
表1 微带八木天线参数Tab.1 Microstrip Yagi-antenna parameters 单位：mm

Python-HFSS联合仿真PSO算法如下所示。将在HFSS中录制的py脚本文件中的非导包部分复制到伪代码图示中的第6行，即可在Python中完成HFSS程序的调用工作。

算法:Python-HFSS联合仿真PSO算法程序内置参数设置:惯性参数ω,学习因子c1和c2;输入:种群代数G;种群规模NP;粒子维度Dim;输出:最佳适应度值fitness;取得最佳适应度值的粒子位置dr,ɡ1 和 ɡ2。1.g ← 1(initialization);2.初始化粒子位置:xki,Dim=rand()(xmax_bondary,Dim-xmin_bondary,Dim);3.初始化粒子速度:vki,Dim=rand()NP;4.while (g ≤ G)do5. fori=1 to NPdo6. f(xki,Dim) ← 代入HFSS中计算xki,Dim处的适应度值(S11参数值);7. 更新粒子i的局部最优位置pbestki,Dim;8. 更新整个种群的全局最优位置ɡbestkDim;9. fori=1 to NPdo10. 更新粒子的速度和位置;11. vk+1i,Dim=ωvki,Dim+c1rand()(pbestki,Dim-xki,Dim)+c2rand()(ɡbestkDim-xki,Dim);12. xk+1i,Dim=xki,Dim+vk+1i,Dim;13. g++;14.returnfitness,ɡbestGDim;

在联合仿真算法运行时，Python与HFSS中的计算、预测或仿真的相关进程是按顺序串行执行的，Python软件线程与HFSS软件线程交替执行，在一个软件执行时，另一个软件处于线程等待状态。由于轻量化的Python的CPU占有率比HFSS软件仿真低，联合仿真算法全时段的CPU占有率相应地也会更低，所以对计算机的配置与算力要求并不高。

3 经典PSO算法的联合仿真实现

使用16 GB内存，主频2.9 GHz,处理器为i5-9400F的主机进行联合仿真，该天线进行仿真计算的频带范围为2～3 GHz，求解步长为0.05 GHz。收敛过程的部分代数的粒子分布如图3所示，坐标轴由左至右分别代表dr，ɡ1，ɡ2的取值，可以清晰地看到粒子种群从均匀分布到逐渐收敛的优化过程。初始化种群中的粒子的分布相当均匀，相比于随机均匀分布，给粒子的搜索提供了极大的范围，经过30代的收敛后，粒子聚集在了dr=32.40 mm，ɡ1=15.71 mm，ɡ2=16.02 mm附近。经测试，此处附近各参数误差为0.5 mm的S11值均在-20 dB以下，以此参数设计的天线具有较好的鲁棒性，在一定的加工误差范围内也可以正常工作。

天线的S11参数图与增益方向图如图4所示，可以看到，在2.5 GHz处的S11参数已经达到了-43 dB左右，远超过一般天线的设计要求。得益于微带八木天线良好的方向性，其最大增益方向始终朝向引向阵子方向。天线参数设计的结果符合实际需要。

在算法效率方面，传统PSO算法下的适应度值变化趋势如图5所示。图5(a)反映了种群寻优及收敛的情况，图5(b)则能清晰地反映出粒子变化的规律，当整个种群的平均适应度值不再下降时，可以认为整个寻优过程找到了最佳区域[14]。结合适应度值的变化规律以及粒子的分布状况，算法在第5代到第10代就已经趋于收敛了，相当于只需要100次左右的仿真，就可以得到S11参数为-40 dB以下的不错结果，这是蒙特卡罗方法[15]仿真无法做到的。在算法运行时间方面，Python中整个程序的执行时间在30 s左右，HFSS仿真一次的时间约100 s，30代的仿真共需要48 030 s。

n

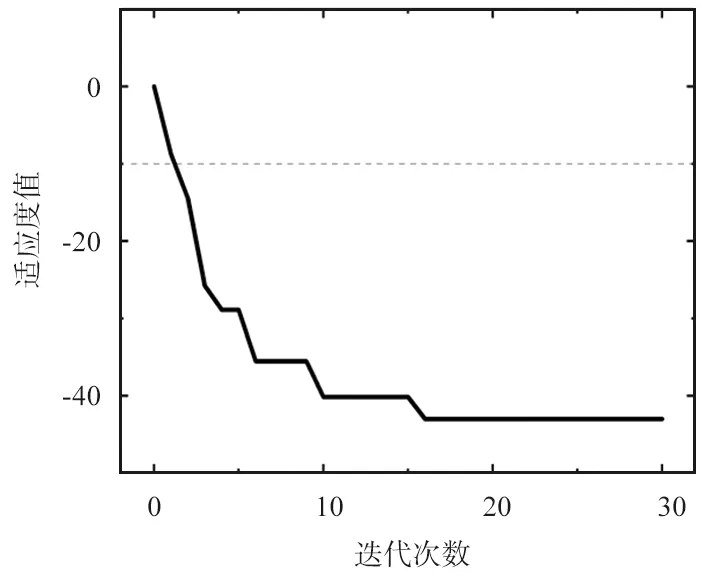
(a) 最佳适应度值变化趋势

(a) 最佳适应度值变化趋势

4 联合仿真的算法改进及实现

通过算法逻辑的构建，可以看到除了对其初始化过程进行OATS改进外，还可以对算法的各个过程根据需要进行针对性的改进，常见的改进有改进粒子的进化策略[16]、在取值边界改变触界逻辑[17]及采用小生境技术[18]等。本文引出一种改变粒子进化策略的FEPSO算法，其思想是将某些代数的适应度值预测过程由仿真变为预测，以节省仿真的时间[19]，在天线优化设计中能够节省大量的时间。下面将给出简略的公式推导过程。

首先，给出由式(1)和式(2)整理得到的新的位置更新式：

(4)

(5)

将这2个公式进一步整合，可以得到粒子xi的k+1代位置的表示:

(6)

(7)

由于不同天线目标值随参数变化产生的峰值函数各有不同，收敛速度以及寻优快慢也有所不同，式(7)中的β为特定天线下的修正系数，最佳适应度值前期变化迅速而后期趋于稳定，预测适应度值算法的修正系数随代数不断降低。c为一个与具体天线有关的常数(为了展示方便，本文取1)，由于天线参数的峰值函数略有不同，预测算法对适应度值的预测程度有整体的偏移，当其劣于计算适应度时，应当取略大于1的数，反之则小于1。于是，可以通过第k-1代与k代粒子i的适应度值推测出下一代的适应度值。使用改进FEPSO算法优化天线的一般步骤如下：

① 在HFSS中对待优化的天线进行建模。

② 确定包括基于OATS的种群位置、惯性因子、认知及社会因子等，完成PSO算法的初始化设置。

③ 将 HFSS 模型作为PSO的适应度值函数，以生成的种群初始值计算各个粒子的适应度值，依次按式(1)和式(2)更新粒子的速度和位置。

④ 使用预测适应度值的方式。在使用预测的代数，根据粒子的前代位置和适应度值等，利用式(7)预测下一代的粒子适应度值，同时通过式(6)更新粒子位置。

⑤ 使用仿真计算适应度值的方式。重复一次或多次步骤④后，再次以 HFSS 模型作为PSO的适应度函数计算每个粒子的适应度值，按式(1)和式(2)更新一次粒子的速度和位置，降低预测可能带来的错误。

⑥ 重复步骤④和步骤⑤，直到达到迭代次数上限或满足预设条件则结束算法。

在规定代数使用适应度值预测算法，可以节约在HFSS中仿真所消耗的时间，使用预测代数越多，节省的时间也越多，但相应地，连续多次的预测会使算法的精度下降。本文在第2代之后的偶数代使用预测方法来优化本文图1所示的微带八木天线参数，参数设置和种群初始化方式依然与表1相同。在进行了同样30代的仿真之后，最终得到的参数粒子收敛后聚集在dr=32.25 mm，ɡ1=15.58 mm，ɡ2=16.07 mm处，此处S11参数的最小值为-46 dB，与传统PSO算法所得到的结果相差极小，这种微小的差异是由程序的随机性导致的，程序优化的目标是一个多峰函数，且由于预测算法中欧氏距离不可以为0，所以最终收敛的点不会完全重合。

FEPSO算法的最佳适应度值变化曲线与种群平均适应度值变化曲线如图6所示。可以看出，其适应度值变化曲线与传统PSO相差不大，由于天线的修正系数β为默认值1(未修正)，预测代数的种群平均适应度值会优于真实值，收敛曲线呈现锯齿状，此时只需要将此值减少即可。而程序运行时间方面，FEPSO算法中第3代以后的偶数代计算均在Python中运行，即在30代的迭代中节约了共计14代HFSS中的仿真时间，整个程序运行用时约26 000 s，在优化结果准确度基本不变的情况下，算法效率较改进前提升了40%以上。

5 结束语

在机器学习技术迅速发展的今天，计算机辅助设计方法与各学科的交叉结合已经是大势所趋。而在天线设计愈加小型化、精细化的大趋势之下，利用传统的蒙特卡罗方法和全波仿真结合的策略所带来的计算量的要求往往是快速迭代的商业应用和微波系统所无法承受的。本文以经典微带贴片八木天线作为切入点，通过引入Python-HFSS联合仿真的技术，详细介绍了联合仿真的细节以及原理，将算法思维与天线设计相结合起来，设计了一款传统的微带八木天线。本文研究了一种能够预测适应度值的带修正系数的FEPSO算法，通过对传统PSO算法的改进，对相同天线的参数进行重新优化，以更高的优化效率得到了相似的效果，良好的优化结果表明了该算法与天线结合的高效性，对于其他复杂天线的尺寸优化同样具有一定的泛用能力。

本文提出的 FEPSO 算法预测模型依赖于种群前代的收敛情况，在前期仿真次数不够多、样本量不够大的情况下，随着代数的增多，预测精度会有一定程度的下降。在之后的工作中，拟加入预测值精度判断算法模块，在精度不足的情况下模块将调用HFSS进行仿真以保证整个算法的精度不会损失太大。