基于预编码联合压扩算法降低GFDM系统PAPR的研究

谷玉婷，刘春刚*，田欣欣，谭 畅，王 钢，杨珊珊

(1.河北师范大学中燃工学院，河北 石家庄 050024；2.哈尔滨工业大学 电子信息工程学院，黑龙江 哈尔滨 150001)

0 引言

随着第五代移动通信系统在全国范围内的普及推广[1]，广义频分复用 (Generalized Frequency Division Multiplex,GFDM)满足未来多载波调制技术的要求[2-3]，将GFDM技术应用于卫星通信系统，其具有传输干扰低、带外辐射小和频谱效率高等优点，已经得到了广泛的重视以及大量的深入研究。 但是，GFDM多载波系统为块状调制，在传输过程中某一时刻可能会出现相位一致导致峰均功率比(Peak-to-Average Power Ratio,PAPR)过高[4]。由于较高的PAPR通过功率放大器时会产生严重的信号非线性失真，GFDM系统的误码率(Bit Error Rate,BER)性能会更加恶化，PAPR过高对功率放大器的设计会有较高的限定要求；另外，采用动态范围大的功率放大器通常需要较高的成本，严重影响了系统传输性能以及日益复杂的通信需求，因此采取一系列措施降低GFDM系统的高PAPR成为重中之重。

现有的降低PAPR技术可分为信号预畸变和信号非畸变2类。信号预畸变类包括限幅法[5]、线性压扩算法[6]和非线性压扩算法[7]等；信号非畸变类包括预编码算法[8]、选择映射SLM法[9]和部分序列传输PTS法[10]等。以上算法中，预编码算法联合非线性压扩算法具有一定的优势，能够在抑制PAPR性能和系统BER之间取得折衷。

预编码类技术通过在发送端对原始数据序列进行预编码矩阵乘法变换，不需要传输额外信息，再进行GFDM调制，在接收端通过解预编码矩阵解调出数据，通过降低信号之间的非周期自相关性使得系统PAPR得到抑制，此方法不会产生严重的信号失真，具有良好的应用背景[11]。文献[12]提出利用BIDFT和DFT的预编码方案均能显著降低PAPR。文献[13]提出的利用WFRFT预编码变换降低GFDM系统的PAPR具有显著效果。

非线性压扩算法属于信号畸变的一种,其思路为通过对压扩后信号样点的幅度满足的概率密度函数(Probability Density Function，PDF)进行函数变换。文献[14]对压扩后信号的PDF采用半sin函数定义，只改变输入信号的幅度，不改变相位。文献[15]压扩后对小幅度信号PDF不做处理，对大幅度信号PDF采用三角函数定义进行压缩。文献[16]对于小幅度信号在原始PDF的基础上适当地缩放，然后将缩放后的PDF在拐点处的切线作为大幅度信号PDF的线性分布。

为了更好地抑制GFDM系统PAPR性能并对系统BER产生较小的影响，本文把预编码类技术和压扩类技术相结合，提出了一种基于DHT预编码矩阵的Cos分布非线性压扩抑制PAPR的联合方法——DHT-CosNC (Discrete Hartley Transform Precoding-Cos Nonlinear Companding)。该方法通过DHT预编码方法和Cos压扩函数实现信号非周期自相关性的调整以及信号幅度的改变以抑制其PAPR。仿真结果表明,本文算法能达到更优的PAPR抑制效果且对系统BER性能影响较小。

1 GFDM系统性能分析

1.1 GFDM系统模型

GFDM多载波系统模型如图1所示。

图1 GFDM系统模型Fig.1 GFDM system model

二进制序列b经过信道编码后，通过QPSK调制，完成相应的星座映射。由于GFDM复数据符号采用块状方式调制，将编码数据映射到包含N个元素的数据块，分解为K个子载波，每个子载波有M个子符号，即总共符号数为N=KM,得到一个由复数据符号组成的序列S=(S0,S1,…,Sk,…,SK-1)Τ，k∈[0,K-1]。上采样因子为L，sk,m表示第k个子载波m个子符号中传输的数据，则经过串并(S/P)变换后可以得到时-频二维GFDM数据矩阵S为：S=(S0,S1,…,SK-1)Τ，即：

(1)

在GFDM调制过程中，每个复数据符号sk,m在发送前都需要用各自循环脉冲成形滤波器进行时域成型滤波和频域上变频变换，被各自子载波的中心频率调制再叠加得到发送信号s[n]，添加CP，最后将数据传入信道进行发送[17]。这样,GFDM发送信号:

(2)

gk,m[n]=g[(n-mK)modN]e-j2πnk/K，

(3)

式中，gk,m[n]为原型滤波器g[n]在时频域上的移位形式，n为采样索引；modN为以N为周期的循环移位；e-j2πnk/K为在频域上的移位操作。

1.2 PAPR性能分析

一个完整的GFDM信号是M个符号上各个载波上的信号叠加在一起的信号。通常情况下，在传输过程中，多个子载波随机叠加后发送会产生较大的PAPR。GFDM是一个多载波系统，当N个子信号都以相同的相位求和时，所得到的信号的峰值最大功率是平均功率的N倍，则PAPR可以表示为：PAPR=10lgN，当N不断增加时，PAPR的值也会呈现线性增长趋势。

在GFDM系统中,信号的PAPR定义为这个数据块内信号峰值功率与数据块内所有采样点功率的平均值的比，表示为：

(4)

式中，Ppeak为GFDM信号峰值最大功率；Paverage为GFDM信号平均功率。

分析GFDM基带输出信号的归一化瞬时功率，由式(2)可得：

p[n]=s[n]s*[n]=

n=0,1,…,N-1,m=0,1,…，M-1，

(5)

(6)

式中，qm(k1,k2)为同一时隙不同载波间符号的非周期自相关函数。将式(6)代入式(5)得到：

(7)

从式(7)可以得出，GFDM信号瞬时归一化功率与滤波器的归一化功率和同一时隙不同载波间符号的自相关性密切相关。本文从降低不同载波间符号的自相关性入手来降低系统的瞬时功率，输入信号的非周期自相关函数的值相加之和越小，输出信号的功率最大值也就越小。因此，本文采用预编码矩阵的正交性来降低符号间非周期自相关函数，从而降低GFDM信号的瞬时功率，使系统的PAPR得到一定程度上的抑制。

通常，采用互补累积分布函数(CCDF)来衡量降低PAPR方法的有效性，CCDF定义为PAPR超过一个给定的阈值ξ0的概率，即：

CCDFxn(ξ0)=Pr(PAPRxn>ξ0)=

1-(1-e-ξ0)N。

(8)

因此，通过预编码器Hm降低符号间的自相关性，从而降低子载波相位一致的概率，就可以达到降低PAPR的效果。

2 DHT预编码技术降低PAPR原理及算法

在基于预编码矩阵的GFDM系统中，经过验证，离散哈特利变换预编码矩阵(DHT-Precoding)是目前一种较好的正交预编码矩阵，其对各时隙传输的复数据序列进行预编码处理，降低各符号之间的周期自相关性，能够有效地降低GFDM信号的瞬时功率，从而抑制系统的PAPR性能。在接收端，可以通过预编码矩阵的逆运算重建初始数据，并且不会对系统的BER性能造成影响。其变换是一种基于实数域的可逆的线性映射，H:X(n)→Y(n)，X(n)为DHT预编码变换前的实数数据，Y(n)为DHT预编码变换后的实数数据。

X(n)的离散哈特利变换可以表示为：

(9)

式中，n=0,1,…,N-1；casθ=cosθ+sinθ。

DHT的可逆矩阵表示为：

(10)

离散哈特利变换矩阵H={hm,n}M×M中的元素为：

(11)

式中，hm,n为DHT矩阵中的第m行第n列元素。

为保证DHT预编码后信号平均功率不变，DHT预编码矩阵是归一化矩阵，表示为：

(12)

经过预编码器对复数据符号进行预编码处理得到新的符号数据，表示为：

(13)

通过DHT预编码变换后的信号经过GFDM调制得到的时域信号表达式为：

(14)

最后，接收端通过预编码的逆矩阵对其进行解码即可还原原始的数据块数据：

(15)

3 提出的2种降低PAPR原理及算法

3.1 Cos分布非线性压扩算法

为了更好地抑制GFDM系统的PAPR性能，且不产生较大的信号失真，在原有压扩算法的基础上提出了一种Cos分布非线性压扩函数。此方法通过定义压扩后新的信号幅度分布特定的概率分布，反向推导出相应压扩函数的形式。为了降低复杂度和方便反向推导压扩函数，定义PDF为连续可导函数。在计算压扩函数时只关注压扩后信号的分布特性，并且压扩后GFDM信号采样点的幅度满足的PDF有较低的PAPR。Cos函数作为压扩后信号概率密度分布函数的方法，只对信号的幅度进行变换，保持其相位不变。本文通过对压扩后信号的PDF进行横纵坐标尺度的缩放和平移,表示为：

(16)

式中，xc[n]为压扩信号；N,k,w为函数变量。

需要满足的条件为：

根据PDF的性质：

随着系统子载波K的不断增加，根据中心极限定理和高斯分布的性质，可得压扩前|x[n]|幅值的PDF为：

(17)

F|xc[n]|(x)=Pr(|xc[n]|≤x)=

(18)

为了保证压扩前后GFDM发射信号在每个GFDM信号块上的平均功率保持不变，表示为：

E(|xc[n]|2)=E(|x[n]|2)=

(19)

即：

(20)

经过多次计算得到：

(21)

假设压扩函数是递增函数：

F|x[n]|(x)=Pr{|x[n]|≤x}=

Pr{|xc[n]|≤c(x)}=F|xc[n]|(c(x))，

(22)

经过计算求解，则压扩函数为：

(23)

由式(23)得到压扩函数的计算式为：

(24)

压扩变换后GFDM系统传输信号可以表示为：

(25)

在接收端，通过计算可以求得反压扩函数，通过反压扩函数对复数据进行解压扩，其反压扩函数为：

(26)

根据式(21)可知，k参数可由w计算得到。因此，通过适当调整参数w，可以更好地降低大幅值信号出现的概率，实现不同程度的PAPR降低和误码率性能之间的有效折衷。

3.2 DHT预编码联合Cos分布非线性压扩算法

为了达到更优的PAPR抑制效果且不增加系统实现的复杂度，图2给出了基于DHT预编码技术和Cos分布非线性压扩联合算法的系统模型，并作为混合技术应用于GFDM系统来降低PAPR。在GFDM发射机的频域采用DHT预编码算法，利用矩阵正交性破坏载波间的自相关性，抑制效果相对差一些，但是几乎不影响系统的误码率；在时域采用Cos函数压扩的算法，使得PAPR抑制效果更明显。采用频域DHT预编码和时域Cos压扩联合算法，抑制效果会更加明显，且对系统误码率影响不大，实现了二者的折衷效果。

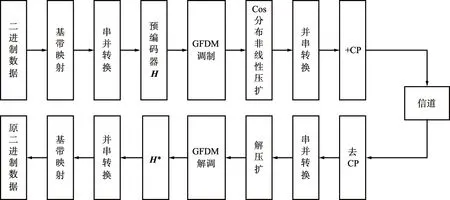
图2 降低系统PAPR流程Fig.2 Flowchart of reducing system PAPR

实现步骤为：

① 首先通过输入的二进制数据流经过 QPSK 星座映射和串并转换后，通过预编码器在数据发送端对数据预编码处理，破坏数据间的自相关性，最后进入GFDM调制。

② 对GFDM调制出的数据进行并串转换，通过Cos函数非线性压扩算法对数据进行压扩，对压扩后的数据加上CP传入信道发送数据。

③ 对接收的数据去CP，利用推导出的Cos非线性反压扩函数解出数据，对数据进行串并变换后进行GFDM解调。

④ 在已知预编码矩阵时不需要传输额外信息，将GFDM解调出的数据送入解预编码器，通过计算预编码的逆矩阵解调数据，进行并串变换,QPSK星座解调，最后解调出二进制数据。

从理论上分析，本方法基于预编码变换联合Cos非线性压扩算法能够达到更优的PAPR抑制效果。

4 仿真实验结果与分析

通过Matlab仿真对本文所提出的基于DHT预编码矩阵的Cos分布非线性压扩技术抑制PAPR的方法理论进行仿真验证。仿真参数设置如表1所示。

表1 GFDM系统仿真参数Tab.1 GFDM system simulation parameters

可以通过调整本方案中的PAPR来获得期望的PAPR降抑制水平。DHT-Cos联合算法和其他算法的PAPR性能比较如图3所示。

图3 DHT-Cos联合算法和其他算法的PAPR性能比较Fig.3 PAPR performance comparison between DHT-Cos joint algorithm and other algorithms

由图3可以看出，当w不断增大时，本文提出的方法将获得更显著的PAPR抑制效果。因为w的增加会使参数N增加而w/k减少，所以大幅度信号出现的概率会降低。当CCDF=10-3时，本文提出的DHT预编码矩阵的Cos分布非线性压扩技术(w=4)提供了最显著的PAPR抑制效果，比其他方法性能更优。

在4PSK下GFDM信号与采用DHT-Cos压扩后信号的PAPR的比较如图4所示，取50个符号。由图4可以看出，GFDM信号的PAPR数值较大，且数值变化较明显，经过 DHT-Cos联合算法后，PAPR比原始GFDM信号的数值降低了7.43 dB左右，且在趋于一定的数值内变化。本文提出的联合算法在降低PAPR方面效果是显著的。

图4 GFDM信号与采用 DHT-Cos联合算法后信号的PAPR值的比较Fig.4 Comparison of PAPR value between GFDM signal and signal using DHT-Cos joint algorithm

在提高PAPR性能的同时也要兼顾系统BER性能， DHT-Cos联合算法和其他算法在AWGN信道上的误码率性能的比较如图5所示。

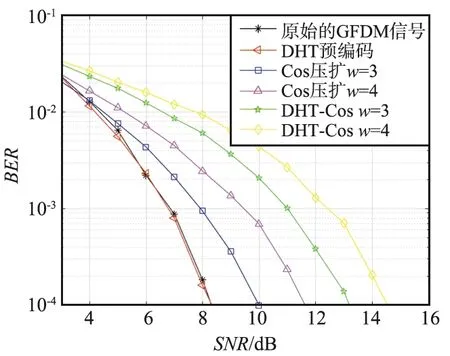
图5 DHT-Cos联合算法和其他算法在AWGN信道上BER性能比较Fig.5 Comparison of BER performance between DHT-Cos joint algorithm and other algorithms in AWGN channel

由图5可以看出，当SNR较小时,Cos分布非线性压扩(w为3,4)和DHT-Cos联合算法(w为3,4)比DHT预编码略差些，因为DHT预编码矩阵是正交矩阵，在AWGN下的BER性能和原始GFDM信号大致相同。在BER=10-4时，DHT-Cos联合算法的SNR在13～15 dB，由于该算法属于非线性过程，会降低大幅值信号出现的概率，因而会牺牲少量的BER性能，但其PAPR抑制程度是几种方法中最为显著的。

5 结束语

本文主要针对GFDM多载波系统的PAPR性能进行了优化。为了显著地提高GFDM系统的PAPR抑制效果，提出了基于DHT预编码矩阵的Cos分布非线性压扩联合算法抑制PAPR。结合抑制PAPR效果和BER性能仿真结果分析，本文算法具有一定的优势特性，可以在此基础上继续研究，使系统BER达到更优的效果。