“双减”背景下初中数学分层作业设计的实践与思考——以“2.4 线段、角的轴对称性(1)”为例

袁 秀

(江苏省南京市文枢初级中学,210006)

一、分层作业设计背景

2021年教育部发布了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》(下文简称“双减”),其中鼓励布置分层作业、弹性和个性化作业.

笔者在教学时也发现,由于学生的认知水平、思维特点以及身心发展不同,传统的“一刀切”布置作业已经不能适应不同层次学生的需求,不利于培养学生学习数学的兴趣及发展学生的个性.

这就要求我们积极探索分层作业和个性化作业的设计.

二、分层作业设计思路

以苏科版八上“2.4线段、角的轴对称性(1)”为例，笔者编制了分层作业:A类题6题,B类题6题,C类题1题,个性化作业1题.A类题与B类题考查知识点一一对应,但A类最简单,B类难度中等,C类题是中考改编题或综合提高题,难度最大,个性化作业相对开放一些,具有趣味性、探索性、开放性.

1.知识点的设计一以贯之,夯实基础,关注基本概念的理解

(A类)1.线段是______图形；______是它的对称轴.

2.线段的垂直平分线上的点到______的距离相等.

(B类)1.如图1,利用网格在图中画线段AB的垂直平分线.

2.如图2,在∆ABC中,已知DE垂直平分AB.若∆ACD的周长是10 cm,AC=4 cm,则BC=______cm.

设计说明对于新授课知识点的考查,A类题利用填空题让学生直接写出知识点,复习本节课知识要点;B类题则考查学生在复杂背景下对概念的理解与应用,对学生掌握知识点的要求相对A类题要高一些.

2.A类解答题给予思路提示,弱有所写,关注后进生的发展

(A类)4.如图3,在∆ABC中,E是BC的垂直平分线l上的一点,若AE=3 cm,EC=6 cm,求AB的长.(提示:由条件DE是BC的垂直平分线可以得到哪两条线段相等?)

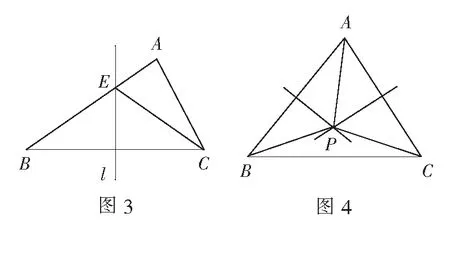
(A类)5.如图4,在∆ABC中,AB,AC的垂直平分线相交于点P.求证PB=PC.(提示:由点P在AB的垂直平分线上可以得到哪两条线段相等?点P在AC的垂直平分线上可以得到哪两条线段相等?)

设计说明A类题的每一道解答题都给予学生必要的思路点拨,让几何学习能力弱的学生在写解答题的过程中有所方向.

3.A类与B类题一一呼应,层次分明,体现几何推理的难易

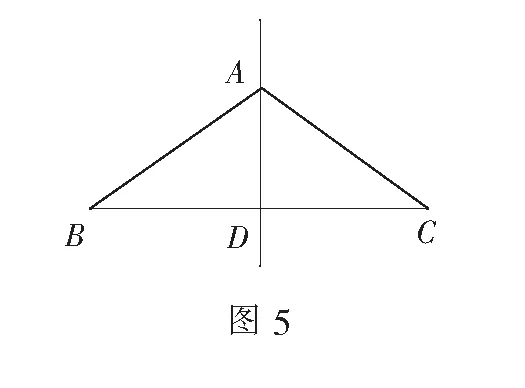
(A类)3.如图5,AD⊥BC,BD=CD,AB=3 cm,则AC=______cm.

(B类)3.已知A,D两点在线段BC的垂直平分线上,且点A,D到BC的距离分别为3,4,则AD的长度是______.

设计说明A类题一步推理,直接运用当天所学知识点,B类题需要自己画图,关注分类,层次分明.

(A类)5.如图6,在∆ABC中,AB,AC的垂直平分线相交于点P.求证PB=PC.

(B类)5.如图7,在ABC中,AB,AC的垂直平分线相交于点P,过点P作PM⊥BC,垂足为M.求证:M为BC的中点.

设计说明A类题与B类题属于同一背景,A类题所有线给齐,不需要学生添加辅助线,B类题需要根据题意添加辅助线,适应不同层次学生的需求.

(A类)6.如图8,在∆ABC中,AB,AC的垂直平分线分别交BC于D,E(点E在线段DC上).(1)若BC=12,求∆ADE的周长;(2)若∠BAC=110°,则∠DAE的度数为______°.(提示:由点D在AB的垂直平分线上、点E在AC的垂直平分线上可以得到哪两对线段相等?由∠BAC=110°可以得到∠B+∠C=70°,还可以得到哪两个角的和是70°?)

(B类)6.如图9,在∆ABC中,AB,AC的垂直平分线分别交BC于D,E(点E在线段BD上).

(1)若BC=12,DE=4,求∆ADE的周长;

(2)若∠BAC=70°,则∠DAE的度数为______°;

(3)若BC=a,DE=b,则∆ADE的周长为______;若∠BAC=α°,则∠DAE的度数为______°.

设计说明A类题图形相对简单,B类题中两条垂直平分线相交,图形复杂,学生需要分离出基本图形,再解决问题,还渗透了从特殊到一般的数学思想,对数学能力强的孩子也是一种锻炼及提高.

4.C类题综合提升,贴近中考,紧跟中考命题方向

在∆ABC中,AB,BC的垂直平分线l1,l2相交于点O.

(1)如图10,若∠1=α°,则∠B=______°,∠AOC=______°;

(2)如图11,若∠1=90°,则∠B=______°,∠AOC=______;

(3)如图12,若∠1=α°,则∠B=______°,∠AOC=______°.

设计说明本题根据2020年南京市中考卷第15题进行改编,将原题中的“∠1=39°”一般化为α°,并探究在锐角三角形、直角三角形、钝角三角形中∠B与∠1,∠AOC与∠1的关系,也为初三学习圆心角与圆周角的关系作铺垫.

5.个性化作业足够开放,激发思维,提高数学思维能力

操作探究如图13,某奶茶店有一块锐角三角形的墙面需要涂油漆,现要在墙面上留一块区域作心愿墙,要使这个区域内的所有点P满足PC≤PA≤PB,请在图中用阴影表示出所有点P组成的区域.

如果墙面为直角三角形呢?钝角三角形呢?

设计说明首先是画出锐角三角形内满足PC≤PA≤PB的所有点P,总结出PC≤PA是AC垂直平分线偏点C的所有区域,PA≤PB是AB垂直平分线偏点A的所有区域,最终满足条件的所有点P组成的区域是以上两个区域与三角形的公共部分.如果墙面为直角三角形、钝角三角形,则需要分别对∠A,∠B,∠C是直角、钝角分三类进行画图.

三、 分层作业设计反思

1.钻研教材,分层设计作业

教师在设计分层作业前,要认真钻研教材,深刻理解本节课的知识点,制定分层目标,设置分层作业.对于数学学习能力弱的学生设置A类题,低起点,以基础题为主,解答题设置为一步推理、两步推理,拆分小题,补台阶,并给予必要的思路提示,让这部分学生也能体会到完成数学作业的快乐;对于数学能力中等的学生设置B类题,起点高一些,以中档题为主,涉及分类思想、逆向思维,指向学生的最近发展区,激发学习学习数学的兴趣;对于数学能力强的学生设置C类题及个性化作业,高起点,高要求,以综合题和中考改编题为主,鼓励学生一题多解,提高学生数学思维能力.

2.了解学生,分层布置作业

教师在布置作业前应深入了解学生学习数学的能力情况,数学学习能力弱的学生选择A类题,数学能力中等的学生选择B类题,数学能力强的学生选择C类题及个性化作业.学生选题的标准可以根据学生的变化情况进行及时调整,比如选择A类题的学生连续几天作业质量都很高,就可以改选做B类题,以此类推.

3.树立信心,分层评价作业

成功的评价是激励学生学习的有力手段,以不同的标准进行分层评价,更加激励学生学习数学的兴趣.对于数学学习能力弱的学生,做对A类题就给满分,并及时寻找孩子的闪光点、肯定他们的进步;对于数学能力中等的学生做对B类题才给满分,并及时指出需要改进的地方、肯定他们的努力;对于数学能力强的学生需要做对C类题及个性化作业,且能迅速答完及一题多解才给满分,并及时引导学生总结解题方法、肯定他们的数学思维.不同层次的学生给予不同的评价,及时帮助学生树立学学习数学的信心.

4.因材施教,分层评讲作业

课堂上评讲作业时进行有选择性的评讲,对学生出错率比较高及共性的错误教师要给出及时的纠错教学措施.对于数学学习弱的学生,重在夯实基础,教师带领订正.对于数学中等及能力强的学生,重在培养思维及方法总结,教师指导学习.这样才能使不同层次的学生在评讲课堂都获得进步.

总之,分层作业设计、布置、评价、评讲,需要教师花更多的时间去探究.分层作业确实有利于各层次学生的充分发展,有利于学生的数学知识在分层作业中灵活运用,有利于学生的数学能力在分层作业中逐渐提升,有利于学生的数学思维在分层作业中快速拓展,有利于“双减”政策的有效落实.