对半角模型两个重要结论的深入探究——以2019年广州中考第16题为例

刘玉清

(广东省广州市二中苏元实验学校，510530)

一、试题呈现

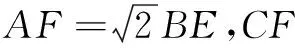
① ∠ECF=45°;

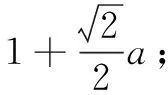
③BE2+DG2=EG2;

其中正确的结论是______.(填写所有正确结论的序号)

二、试题分析

由题目条件,在这两个三角形中,很容易看到以下三个条件，HF=BE,∠FHE=∠B=90°,AE+EB=AE+AH,即HE=AB=BC,所以∆HFE≌∆BCE,所以 ① ∠ECF=45°是正确的.

三、模型提炼

半角模型:如图2(1),在正方形ABCD中,已知E,F分别是边BC,CD上的点,且满足∠EAF=45°,AE,AF分别与对角线BD交于点M,N.

(1)求证:BE+DF=EF;

(2)如图2(2),连结BD,交AE于点M,交AF于点N,求证:BM2+DN2=MN2.

分析证明线段和的常用办法是截长补短构造全等,而本题中若想用过点A作EF垂线的方法来截长,并不能证得全等,所以改用补短法,如图3，延长EB至点F′,使得BF′=DF,连结AF′(也可以将∆ADF绕点A顺时针旋转90°得到∆ABF′,再证明B,E,F′三点共线),可得∆ADF≌∆ABF′(SAS),由两个三角形全等得出其对应边相等(AF′=AF′),对应角相等(∠DAF=∠BAF′);由∠FAE=45°得出∠BAF′+∠BAE=∠DAF+∠BAE=45°,于是∆AEF≌∆AEF′(SAS),得到EF=BE+BF′=BE+DF,由上可知,两次三角形全等可以证得这个线段和的结论.

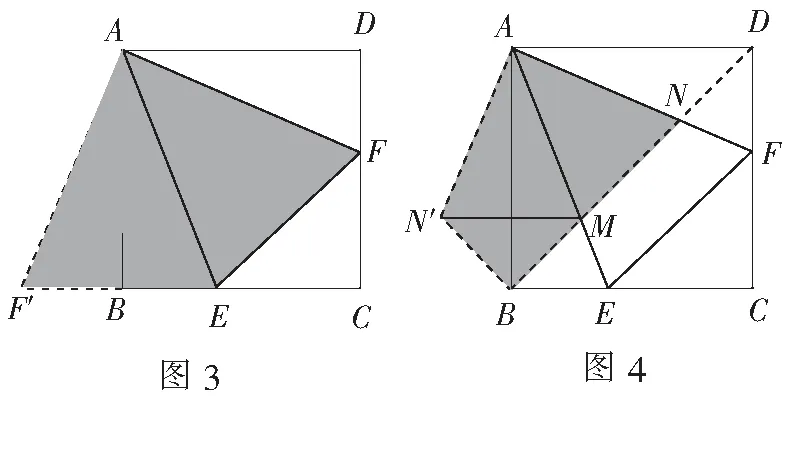
对于第 ② 个结论,我们首先需要将∆ADN绕点A顺时针旋转90°到∆ABN′,从而∆ADN≌∆ABN′,对应线段有DN=BN′,AN=AN′,对应角有∠DAN=∠BAN′,∠ADN=∠ABN′=45°,如图4，从而得到∠BAE+∠BAN′=∠BAE+∠DAN=45°,所以∠EAN′=∠EAN,于是得到第二组全等∆AMN≌∆AMN′,得到对应线段MN=MN′,此时三条线段BM,MN,ND都已集中到一个三角形中,易证∠DBN=∠ABN′+∠ABD=90°,根据勾股定理就可以得出结论了.

四、模型应用

看似简单的两个结论,学生在题目的华丽包装下,总有雾里看花的感觉,有时难以回归到问题的本质,所以解决起来思路并不是很顺畅．我们一起来探讨一下下面的几个典型例题.

分析∠GOD=45°这个条件如何用?45°很特殊,但是直线的位置不特殊,所以角度不好用,那么我们会思考:怎么将45°转移到一个特殊位置呢?

将直线GH平移到特殊的位置,如图6,或者将DE平移到特殊的位置,因为点D为正方形的顶点,所以将直线GH平移到经过点D时半角模型就出现了,这是本题的难点,接下来的解答就已经顺理成章了.

然后,设AE=x,BE=4-x,在Rt∆EBM中,斜边EM如何用未知数表示?根据半角模型结论 ①,可以得出EM=2+x,从而在Rt∆BEN中由勾股定理列出方程，解出未知数,求得结果.

从本题的解答来看,如何在条件的转化过程中发现和构造出半角模型很关键,最明显的特征是直角顶点中处有45°的夹角.

经典题2如图7,正方形ABCD中,点E是AC上一点,点F是EC的中点,EP⊥AB于点P.

(1)连结DF,探究DF与PF的大小关系与位置关系;

(2)连结DP交AC于Q,求证:FQ2=AQ2+CF2.

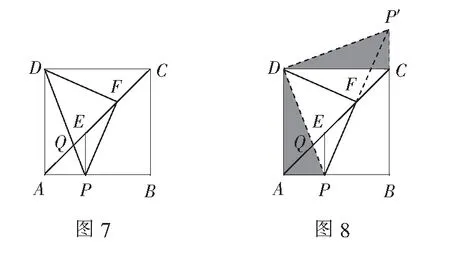
分析第(1)问观察图形中DF与PF的特点,一般我们会得出的结论DF=PF,DF⊥PF,但是如何证明猜想呢?我们不妨想象,如果结论成立,连结DP,∆DFP应该是等腰直角三角形,F是EC的中点、PE⊥AP这两个条件怎么用?由中点条件,我们常用方法是倍长中线PF至FP′,如图8,由倍长中线作出辅助线得到∆EPF≌∆CP′F(SAS),证得P′在BC延长线上,以及F为PP′中点,再由PE⊥AP得到∆APE为等腰直角三角形,所以AP=PE=P′C,从而证得∆DAP≌∆DCP′(SAS),再证得∆P′DP为等腰直角三角形,根据等腰三角形的三线合一,得出结论.

第(1)问提供半角模型所需要的∠FDP=45°,下面证法完全等同于半角模型结论 ② 的证明,也可以先由第(2)问的结论,联想到半角模型,从而得出第(1)问要证明∆DFP是等腰直角三角形.

经典题3如图9，已知在正方形ABCD中,AB=6,P为边CD上一点,过点P作PE⊥BD于点E,连结BP，O为BP的中点,连结CO并延长交BD于点F.

(1)连结OE,求证:OE⊥OC;

四、解题探究

从以上题目中,我们总结出以下三点:

①明确半角模型的条件;

②熟练掌握半角模型的结论(还有很多结论,本文限于篇幅,只研究了这两个结论);

③能够对题目条件进行恰当的转化,从而发现半角模型.

熟练掌握初中平面几何中的一些重要模型,比如“一线三等角”模型(在这组模型中,考查最多的是其中的三垂直模型,射影定理模型,这是相似模型中应用最广泛的模型之一),以及最近几年中考的热点问题“定弦定角问题”、“路径旋缩问题”等等．这些模型对几何题的分析与解答很有帮助,但是知识的迁移能力需要一定的知识储备和经验积累．