2022年北京卷20题第(3)问的多解探究与推广
李锦旭
(北京市育英学校)
题目 (2022年北京卷20)已知函数

(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)设g(x)=f′(x),讨论函数g(x)在[0,+∞)上的单调性;
(3)证明:对任意的s,t∈(0,+∞),有
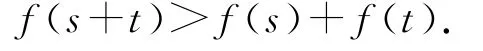
2022年,北京使用新教材的第一届学生参加高考,命题体现了诸多与以往不同的新变化,本题第(3)小题新颖有趣,是这种新变化的典型,这里尝试给出几种解答并予以推广.
思路1 着眼于多变量,采用将双变量分主次的策略.

由于此不等式涉及双变量(s,t),选择其中一个为主变量(另一个为参变量)构造辅助函数如下.

方法2 (抽象函数分析法)将s视为主变量,t为参变量,则可构造关于s为自变量的抽象函数,即
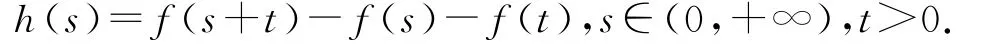
按复合函数求导法则,有
h′(s)=f′(s+t)-f′(s)=g(s+t)-g(t),
再利用第(2)问的结论:g(x)在[0,+∞)上单调递增可得h′(s)>0,故f(s+t)-f(s)-f(t)>0,即对任意的s,t∈(0,+∞),有f(s+t)>f(s)+f(t).
思路2 先放缩后构造辅助函数.
方法3 方法1中的式①看上去较为复杂,那么能否通过化简、放缩等手段优化解题过程呢? 我们知道ex>1+x(x>0)(证明过程略),于是要证明式①,只需要先证明加强不等式

所以r(s)在(0,+∞)上单调递增,有

即es+tln(1+s+t)>esln(1+s)+etln(1+t),即

其实,我们还可以用如下放缩的结论迅速得到

思路3 着眼于研究函数特征,从几何意义视角寻求突破.
方法4 (拉格朗日中值定理)由(2)知g(x)=f′(x),g(x)在[0,+∞)上单调递增,可知函数f(x)=exln(1+x)的图像是向下凸的,基本形状如图1所示.
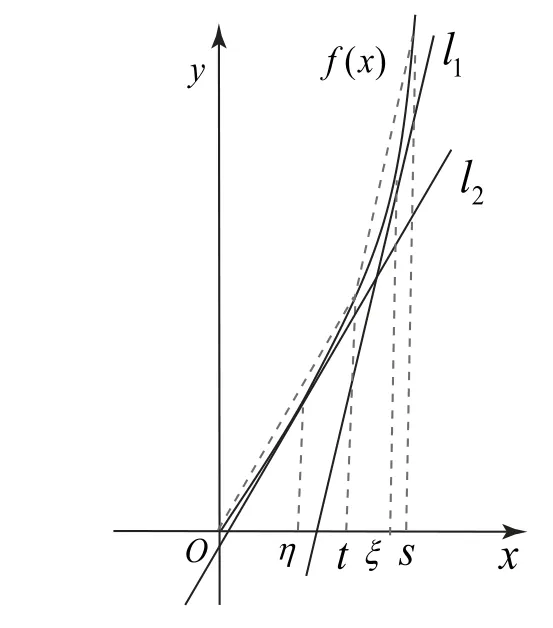
图1
不妨设s≥t>0,则函数f(x)在[0,+∞)上的任意闭区间上连续,相应开区间内可导且端点值不相等,即满足拉格朗日中值定理的条件,故由拉格朗日中值定理可得


故F(x)在(0,+∞)上单调递增.


