偏最小二乘回归模型在EEG特征选择的应用
刘彦俊,王 力
广州大学 电子与通信工程学院,广州 510006
脑机接口(brain computer interface,BCI)是一种将人类大脑和外部设备之间建立通信和控制通路的技术。BCI 系统能够把人的肢体信息和生理信息转换为能够驱动外界器械设备的命令。脑电信号(Electroencephalogram,EEG)具有低成本、高时间分辨率的特点,广泛应用于脑电接口中,其中运动想象能自发产生一种可识别的脑电图信号,不需要外界刺激,特别适合患者的康复训练和运动控制,因此可以帮助如脑卒中偏瘫等有运动障碍的患者得到更加高质量的康复训练[1],并已成功应用于神经生物学、心理学等领域。
到目前为止,已经提出了很多方法来提高识别性能,虽然在这一领域已经取得了很多成果,但大多数算法只能通过进行离线评估,而不能在线评估,是因为在脑机接口领域实验不能让被试长时间地每次执行相同的诱发运动来记录大脑信号,所能得到的训练样本数量非常有限。深度学习模型由于缺乏足够的数据来学习更多可能的特征,使分类器更加健壮和可靠,导致有限的训练数据集无法充分发挥深度学习模型在BCI 领域的潜力。因此,本文提出了一种自动生成更多人工脑信号数据的新方法来克服这一数据不足的问题。
脑电信号作为广泛应用在脑机接口模型中的信号,但是信号弱、低信噪比和空间模糊等特点使得难以提取稳定和具有区分性的特征。因此,特征提取在基于运动想象的脑机接口方向一直是研究热点。此外,特征选择可以降低特征维数和噪声干扰,所选特征更稳定、更具识别力,因此对特征选择的研究也非常重要。目前常用的特征提取方法有:自回归模型(autoregressive,AR)[2],共空间模式(common spatial pattern,CSP)[3]、小波特征[4]等。基于共空间模式的方法在1991 年首先被Koles[5]提出可以使用该方法提取脑电信号中包含的特殊成分。紧接着,Müller-Gerking 等人[6]在1999 年首次提出将这一方法应用到运动想象EEG 信号的分类中,它能有效地提取出运动想象信号中事件相关同步和事件相关去同步的特征,使得两类信号的方差值差异最大化,从而得到具有较高区分度的特征向量,因此在运动想象特征提取中得到了广泛的应用。但因为该提取特征方法对冗余信息敏感度高和泛化能力低等缺陷导致影响后续分类正确率,因此提出一种有效的特征选择方法是提升分类器模型精度的关键。近年来常用的降维方法有主要成分分析(principal components analysis,PCA)[7]、独立成分分析(independent component correlation,ICA)和线性判别方法等。PCA 是用将高维特征映射到低维特征的这部分特征来表示原始数据以此来进行降维,是一种无监督学习,虽然提取的数据在维度上减少了,去除了特征属性间的冗余信息,但是提取的主要成分中没有包含任何类别的信息,可能把有区分度的特征当作冗余信息删除。
因此,提出利用偏最小二乘法回归(partial least squares regression,PLS)对经过共空间模式的数据进行特征选择,解决了PCA 方法中因没有考虑主成分对输出变量的解释能力,方差很小但对输出变量有很强解释能力的主成分将会被忽略掉的缺点。
众所周知,支持向量(support vector machine,SVM)是常应用在两类信号进行分类的分类器。核函数及其参数选择和误差惩罚因子的调整可以影响其分类性能,因此采用粒子群优化(particle swarm optimization,PSO)对SVM的参数选择,采用分类性能最好的参数作为最佳参数。
本文提出了一种CSP-PLS特征提取与降维算法,将利用数据增强方法对数据进行扩充,CSP算法进行特征提取,PLS作为数据降维,最后利用PSO-SVM作为分类器。将经过数据增强的脑电信号利用CSP-PLS 算法应用到2005 年BCI 竞赛集IIIa 中检验算法有效性和可行性,分类正确率结果显示CSP-PLS算法能有效提升脑电信号分类正确率。
1 基于CSP-PLS特征降维算法
1.1 共空间模式(CSP)
CSP 能有效地提取出运动想象信号中事件相关同步和事件相关去同步的特征,使得两类信号的方差值差异最大化,原理介绍如下:
假设Xh∈RN×T表示经过预处理过后的一次运动想象(h∈{L,R},L和R分别代表想象左手运动和想象右手运动)的数据,N代表通道数,T代表样本采样点数。计算每一类的运动想象数据的平均空间协方差矩阵表示如下:

1.2 数据增强
数据增强是通过对训练数据进行变换,生成新样本的过程,目的是提高分类器的准确性和鲁棒性[8]。本文提出利用图像处理中常用的数据增强方法来增加脑电信号的样本数量:在原始训练数据的每个特征样本中加入高斯噪声,以获得新的训练样本,定义一个高斯随机变量z的概率密度函数P:

其中μ代表的是数学期望,决定着概率密度函数P的位置,σ代表的是标准差。由于脑电信号是时域包含大量特征信息,因此在数据增强时,通常选择μ=0 的高斯白噪声。将已经预处理后的脑电数据Xh∈RN×T,h∈{L,R}与概率密度函数P相加得到数据增强数据Xnoise:

Cnoise表示的是μ=0 的高斯白噪声。
1.3 偏最小二乘法回归
PLS是一种多元数据分析方法,通过最小化误差的平方和找到一组数据的最佳函数匹配。建模过程中集成了主成分分析、典型相关分析和线性回归分析方法的特点,因此在分析结果中,除了可以提供一个更为合理的回归模型外,还可以同时完成一些类似于主成分分析和典型相关分析的研究内容,实现数据降维和回归建模。偏最小二乘算法主要分为两种:第一种是多因变量,第二种是单因变量,因为该论文讨论是分类问题,即是单因变量问题,对于目标矩阵Y可以精简利用y向量代替。具体原理如下:
将原始数据进行zscore数据标准化,即XZ=(Xmean(X))/std(X),mean函数是求X矩阵的均值,std函数是求原始数据矩阵的标准差,最终得到标准化矩阵XZ。设有p个自变量X={x1,x2,…,xp}和一个因变量y向量。故自变量组成的数据矩阵X是n×p格式,n为样本点数,因变量组成数据矩阵y为n×1 格式。在X和y中提取出一组潜在成分t1,t1=w1x1+w2x2+…wpxp=wTX,它可以尽可能多的代表自变量数据矩阵X,t1与目标变量y的协方差尽可能最大化。w是代表所对应的投影方向。
计算潜在成分和因变量之间协方差最大化的极值问题。通过下述公式:

t1尽可能代表矩阵Xfeature包含的信息且t1与因变量y相关程度达到最大。得到t1后可以进行对因变量y的回归方程构建得到:
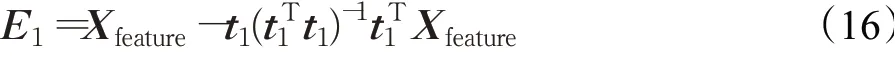
将E1作为新的Xfeature,抽取下一个潜在成分t2,直到残差中包含很少的信息。这一过程循环操作分别提出自变量组与因变量组的成分,在该论文的标准是当前k个成分解释因变量的比率达到接近峰值时且后续增长很少,取前k个潜在成分。
将X中变量的线性组合的PLS 因子,即预测变量得分矩阵作为降维后的特征矩阵。解决了PCA方法没有考虑主成分对因变量的解释能力,方差贡献小但是对因变量具有强解释能力的主成分给忽略掉的问题,它逐层分解因变量矩阵和自变量矩阵,且结合提取的主成分达到对预期精度后停止提取。
1.4 基于粒子群优化的支持向量机
支持向量机是一种属于监督学习算法的机器学习方法,其主要思想将非线性的输入向量映射到一个高维特征空间中,再通过建立一个最优决策超平面,使得该平面两侧距离该平面最近的两类样本之间的距离最大化,从而实现对线性可分样本的最优分类[9]。
SVM通过对核函数及其参数选择和误差惩罚因子的调整可以影响其分类性能,非线性的脑电信号的分类效果与其密切相关,因此选取核函数和误差惩罚因子对分类效果十分重要。该论文采用粒子群优化对SVM的参数选择进行调整和优化并利用交叉检验方式对其选择参数的算法的泛化能力进行衡量,选择分类性能最好的参数作为最佳参数。
PSO 来 源 于1995 年 由Eberhart 博 士 和Kennedy 博士对群鸟觅食过程的行为研究[10],它的基本核心是通过群体中的个体之间的信息共享从而使这个群体的由无序运动转换为有序运动,直到寻找到最优解。在这使用启发式算法PSO进行参数寻优,用网格划分来寻找最佳的参数惩罚因子c和核函数g。对于SVM 参数优化,可以当成对参数(c,g)的最优参数寻找。算法步骤可分为以下步骤:
(1)将随机各自生成初始粒子种群Pm和速度Vm,得到一组初始位置。
(2)将当前的(c,g)作为SVM的参数训练模型,得到一个识别正确率作为适应值,并与设置的适应值阈值进行比较,若没有达到满足则进行位置的更新。
(3)重复步骤(2)直到找到超过适应值阈值的参数或者是达到最大迭代次数为止。
介绍完PSO-SVM 算法后,提出了CSP-PLS 算法,它能解决PCA算法降维仅考虑主成分对自变量的解释程度,缺少对因变量的解释程度的缺点。CSP-PLS算法描述如下:
(1)利用数据增强方法生成人工脑电信号,扩充总脑电信号数量并依次进行后续步骤,得到人工脑电信号的特征矩阵组,将其与原始数据处理后得到的特征矩阵组进行合并。
(2)经过预处理后的脑电数据通过公共空间模式算法滤波,得到能使得两类运动想象信号的方差值差异最大化的特征向量。
(3)利用PLS 对经过(2)处理的特征向量从特征集合中提取几组最具有统计意义的潜在成分向量组,达到降维效果。
(4)利用经过粒子群优化对惩戒参数c和核函数中的gamma函数参数进行优化,得到最优参数作为支持向量机参数对特征向量组进行分类。
详细流程图如图1所示。
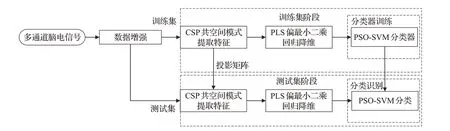
图1 脑电信号算法流程图Fig.1 Flow chart of EEG signal algorithm
2 数据集描述
实验数据是来自BCI Competition III data set IIIa,记录着坐在有扶手的舒适座椅上的被试者四类运动想象任务,包括:左手、右手、脚和舌头。如图2所示,该实验一共包括四个阶段,在t=2 s前,被试一直静坐在座椅上盯着空白屏幕。在t=2 s时刻,电脑将会发出提醒警示,并在屏幕上显示一个持续1 s 的十字符号图像。当t=3~7 s期间,将会出现一个运行想象任务类别的标志符,被试将在这段时间开始执行该类别运动想象任务。
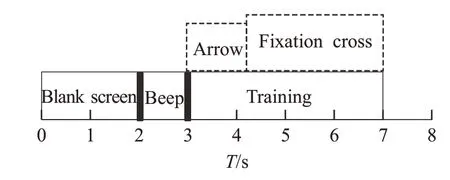
图2 实验时序图Fig.2 Experimental sequence diagram
该数据集是由60 个电极采集的信号,信号的采样频率为250 Hz,将左乳突作为参考电极,右乳突作为地极。其中K3b 被试选择左手和右手运动想象各45 次,K6b和l1b被试选择左手和右手运动想象各30次作为其数据集。
将数据集采用K-fold交叉检验计算分类准确率,即将所有数据分成10 等份,训练集有9 份,测试集有1份。依次将每份都做一次测试集,其余剩下部分作为训练集,重复进行10次,取其平均值作为最终分类正确率。
3 结果
3.1 预处理
该论文将采用三名健康的被试K3b、K6b、l1b 的数据进行分析。大脑在进行运动想象任务时,产生的脑电信号在30 Hz 以下,且表征运动想象一般出现在μ和β节律,对应的频段分别是7~13 Hz 和13~30 Hz,因此将数据先进行8~30 Hz 的带通滤波预处理。滤波可以将多种噪声如:工频干扰,肌电信号等较为常见的噪声去掉,尽可能的得到信噪比更高的脑电信号。期间时间,共1 000 个采样点,有60 个电极,一次想象范式的数据格式为60×1 000。
3.2 脑电信号数据增强与CSP滤波
以下实验均以K3b 数据进行说明。将经过预处理后的K3b 被试的脑电数据进行以不同想象类别进行分段处理,提取4 s运行想象一个类携带45个带标签的范式,则两类运动想象的总体数据为90×60×1 000。
接着进行数据增强步骤,使用的是一个均值为0,方差为4的高斯白噪声信号以相加的方式进行数据增强,具体的公式如式(11)所示。构成一个数据格式为90×60×1 000 的新数据集,使得总体数据扩大了一倍,总体数据变为为180×60×1 000,数据集得到了扩充。
将得到扩充的数据集经过1.1节所描述的公共空间模式特征提取算法进行计算,得到由所有特征向量矩阵所组成的空间滤波器,即是投影矩阵W,取W的前3列和后3 列组成最终的最优空间滤波器,将180 次实验数据经过空间滤波后再进行1.1 节的公式(9)的特征向量归一化得到各自的一维特征向量,总特征矩阵的格式为180×6,记为Xfeature。
3.3 PLS降维
将3.2节经过CSP特征提取后的总特征矩阵Xfeature进行单因变量偏最小二乘算法建模。Xfeature是180×6维格式,即代表有180 次实验,每个实验的提取的特征向量由6 个特征值组成。本文将采用PLS 算法后得到的主成分对Xfeature和目标变量y的累计贡献率作为综合的参考标准,以确定最终选择潜在成分的个数。如图3和图4分别表示自变量提取成分贡献率和因变量提取成分贡献率。
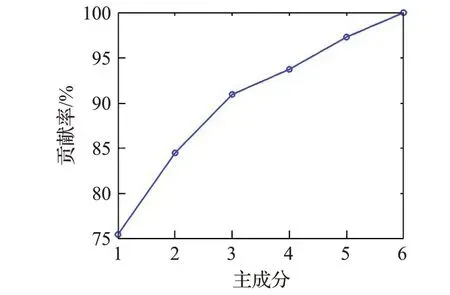
图3 主成分对自变量贡献率Fig.3 Contribution rate of principal component to independent variable
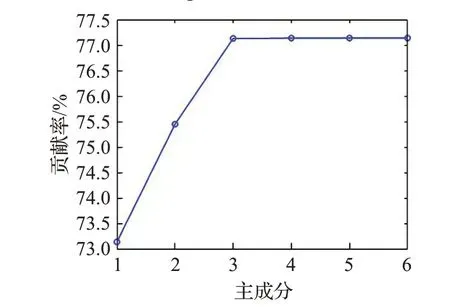
图4主成分对因变量贡献率Fig.4 Contributions of principal components to dependent variables
可见当潜在成分个数为3,已经接近达到累计贡献因变量解释程度的峰值,故选择潜在成分为3。
则用t1、t2和t3这3 个潜在成分作为原始数据Xfeature的低维表示,得到降维后格式为180×3特征矩阵。
3.4 数据增强前后比较
将经过数据增强和PLS降维的特征矩阵进行K-fold交叉检验,经过数据增强后的数据共有180 组实验,均分为10等份,其中9份作为训练集,1份作为测试集,以此进行计算分类正确率。将每1份都作为1次测试集得到10次分类正确率后取其平均值作为最终正确率。
BCI IIIa 数据集的CSP+PLS+PSO-SVM 方法经过数据增强前后的仿真实验结果如图5所示。图5比较数据增强前后3 名被试的平均分类正确率结果,其中K6b被试的数据分类正确率有较大的提升,为4.89 个百分点,其他两位被试K3b和l1b也有相应的提高,分别提高了1.73个百分点和3.05个百分点。3位被试提升的平均分类正确率为3.22个百分点,可见数据增强方法扩充了原始数据集且有效的提升分类正确率。
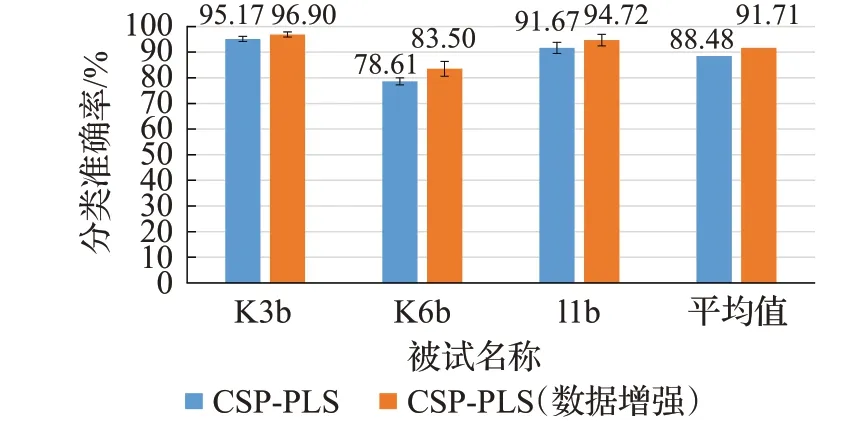
图5 数据增强前后各被试对比Fig.5 Comparison of subjects before and after data augmentation
3.5 PLS算法与PCA算法比较
与PCA 不同,PLS 充分利用了类别向量y的信息。PCA中,最开始对于自变量X,为了找到能最好地概括原数据信息的综合变量,提取了第1 成分F1,使得F1中含有的原数据变异信息可达到最大。而在PLS 分析过程中,先分别在X和y中提取出成分t1和u1,使得这两个成分尽可能多地携带X和y的信息,并且两者的相关程度能够达到最大。在脑电信号分类过程中,因变量个数只有一个,属于PLS 应用过程中单因变量问题。由此构成了自变量X={x1,x2,…,x p}n×p和因变量y={y1}n×1。其中,n为样本的数目,p是特征的数目。根据CSP 算法进行特征提取信号,使用PLS 与PCA 两种特征降维方法得出的特征向量,采用PSO-SVM 分类器进行分类。得到图6的3位被试的分类结果。由图可见,3位被试想象运动的所有试验平均分类正确率经过PLS 算法特征选择后准确率均有提升,其中,被试K6b达到最高的16.01个百分点,3位被试所有试验平均分类正确率为88.48%。可见PLS 方法有效地提取到区分度显著的特征向量,引入了主成分对因变量的解释能力的方法,解决了PCA方法中因为自变量的方差贡献小,但是对因变量具有强解释能力的主成分给忽略掉的问题。
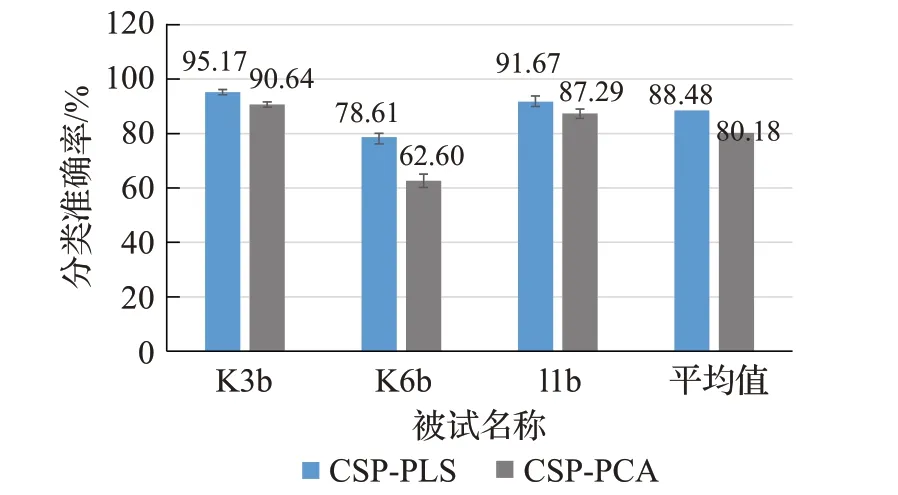
图6 两种特征选择方法分类正确率比较Fig.6 Comparison of classification accuracy between two feature selection methods
3.6 数据增强与PLS算法共同作用

从图7可以看出,分别经过数据增强与PLS算法的3 位被试的分类准确率都有不同程度的提高,K6b 被试分类准确率提高最大,分别提高了14.99 个百分点和13.68个百分点。在数据增强和PLS组合算法作用下的3名被试结果均达到最高分类准确率,其平均分类准确率达到91.71%,比单独进行数据增强和PLS 算法的分类准确率都有相应的提高,这证明了数据增强与PLS结合算法共同作用的有效性。
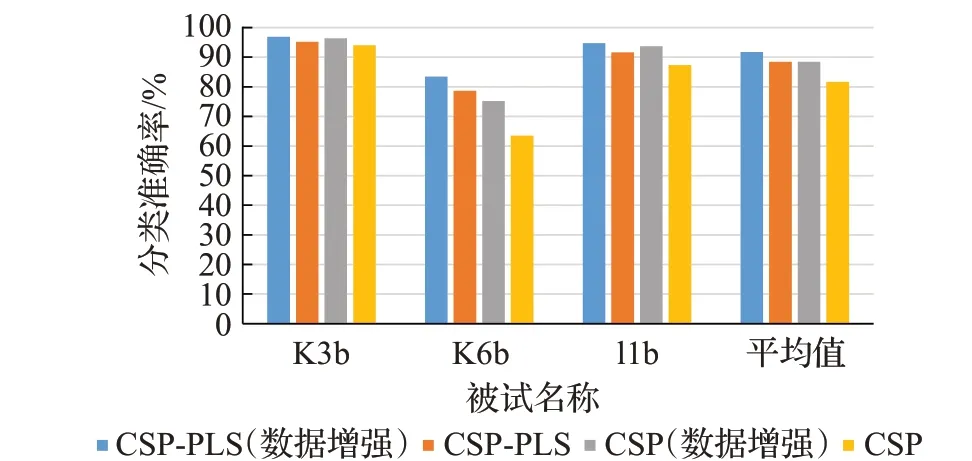
图7 数据增强与PLS结合算法分类准确率Fig.7 Classification accuracy of algorithm combining data enhancement and PLS
3.7 4种特征提取算法比较
如图8比较了4种特征提取方法结合各自的分类器模型得出的分类率,分别是CSP-LDS、CSP、WL-CSP 和提出的CSP-PLS 算法。各种算法的分类性能的统计如图8 所示。从结果显示出,本文提出的算法与Wu 等人[11]提出的基于LDS 变换的CSP 的脑电信号特征提取算法、CSP算法[12]和Wang等人[13]提出WL-CSP算法的分类准确率相比,均高于3组,其中K3b被试的平均分类正确率为96.90%,l1b 被试的平均分类正确率为94.72%,K6b 被试的平均分类正确率为83.50%。可见采用相同的BCI IIIa 数据集的情况下,使用数据增强后的数据集利用CSP 特征提取后再采用PLS 作为特征选择算法相比未使用的其他算法是有明显提高的,本文提出的方法为运动想象信号分类技术准确率提升提供了新的思路。
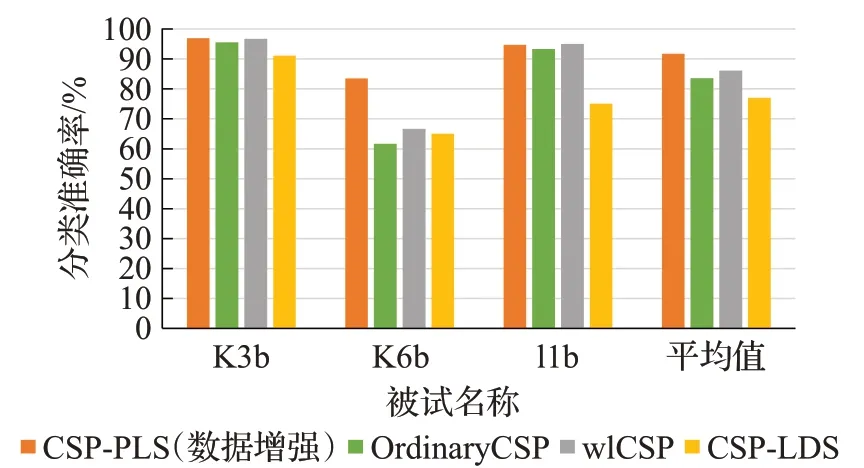
图8 4种算法分类正确率比较Fig.8 Comparison of classification accuracy of four algorithms
4 讨论与总结
针对信号经过共空间模式的数据进行特征选择,本文提出的PLS方法解决了PCA方法中因没有考虑主成分对输出变量的解释能力、部分主成分的方差很小但其对输出变量有很强表征能力也会被剔除的缺点。将数据增强后得到扩充的数据集经过共空间模式滤波提取特征,得到一组特征向量集,再采用偏最小二乘算法进行降维,进一步提取能代表输入数据的主成分,在保证分类正确率的基础上减少了后续分类的时间,使整体的算法时常得到简化,为脑机接口在线分析提供了可行的方法。

