融合拟单层覆盖粗集的集值数据平衡方法研究

吴正江，杨 天，郑爱玲，梅秋雨，张亚宁

河南理工大学 计算机科学与技术学院，河南 焦作 454003

不平衡数据是指数据集内部类别分布不平衡的数据，通常产生于网络安全、异常流量检测、生物信息中的异常基因片段和信用卡支付等领域。在实际生活中，少数类的价值往往要高于多数类。因此，如何有效地提升不平衡数据的分类效果已经引起了广泛学者的关注。现阶段，对于不平衡数据的处理主要分数据层面与算法层面两个方面。对于数据层面来说，通过欠采样、过采样与混合采样的方式，使得数据达到相对平衡。Chen等[1]提出的RSMOTE 模型引入相对密度来测量每个少数样本的局部密度，通过在边界样本和安全样本周围分别进行数据生成来提升边界的可区分性，从而改进分类效果。Li 等[2]提出的SMOTE-NaN-DE 模型基于噪声检测的方法来改进SMOTE 过采样后生成的数据。Ramentol 等[3]提出的SMOTE-RSB 模型通过将SMOTE平衡化后的数据用粗糙集下近似处理，从而提高数据质量。对于算法层面来讲，通过代价敏感学习、集成学习和单类学习等方法改善已有的算法。张壮等[4]提出的Takagi-Sugeno-Kang 模型通过集成学习改进分类能力，徐剑等[5]结合代价敏感学习构建不均衡数据分类器，陆妙芳等[6]通过基于密度和径向基函数来提升过采样能力。在文献[7-9]中，均是通过不同方式改进过采样数据质量来提升不平衡数据的分类效果，在文献[10-11]中，通过不同的机器学习方法来解决不平衡数据分类问题。总的来说，改进数据质量是提升不平衡数据分类能力的重点，其中，如何合理地降低噪声数据的影响也是研究中的热点问题。由于粗糙集下近似具有较高的数据质量，因此作为降低噪声数据的处理手段是可行且合理的。

在一个信息系统中，如果其中包含集值，就称之为集值信息系统[12]。在集值信息系统中，如果只是简单地将集值记录删除，可能会放大该记录带来的影响，尤其是该记录存在于少数类中。因此，将适用于集值信息系统的拟单层覆盖粗集模型与过采样或是欠采样方法结合是一种合理的方案。

容差关系粗糙集与拟单层覆盖粗集是集值信息系统中的两种主要粗糙集模型。Guan 等[13]提出了从集值信息系统中获取决策规则的最大相容类模型。在文献[14-15]中，基于容差关系从不完备信息系统中获取高质量的近似集和决策规则。Stefanowski 等[16]基于非对称相似关系从不完备信息系统中获取近似集和决策规则。Wang[17]处理基于限制性容差关系的不完备信息系统，是粗糙集的进一步扩展。Wu 等[18]在覆盖近似空间的基础上提出了拟单层覆盖近似空间的概念，并提出了近似集集合形式表示的原型。在文献[19]中，讨论了求解集值信息系统中拟单层近似集的问题。与其他基于容差关系的粗糙集模型相比，拟单层覆盖粗集不仅具有更高的近似质量，且因其等价类表示的优点所以具有更快的计算速度。因此，选用拟单层覆盖粗集作为样本区域划分的工具，在集值信息系统中将所属不同区域的样本根据不同的采样策略进行处理，能够有效提高不平衡数据的分类效果。

基于BorderlineSMOTE[20]的分区域处理与SMOTETomek[21]欠采样与过采样混合处理的思想。针对集值信息系统中的不平衡数据，本文提出了SMCRS-BS-CL模型。在SMCRS-BS-CL模型中，首先使用拟单层覆盖粗集（semi-monolayer covering rough set，SMCRS）下近似进行区域划分，将属于下近似的元素划分为可靠的元素，将这一部分可靠的元素使用BorderlineSMOTE模型进行过采样；将不属于下近似的元素划分为边界元素，将这一部分边界元素用ClusterCentroids[22]进行欠采样。模型建立的思想是，对于下近似部分，数据相对来说是质量高数据，因此用过采样方法进行过采，能够极大程度提高分类质量。对于边界元素部分，由于数据相对来说质量较低，因此对其进行欠采样，极大程度保留数据信息。通过利用分治的策略对不同区域的不平衡数据进行处理，能够极大地提升不平衡数据的分类效果。

1 相关工作

1.1 拟单层覆盖粗集

集值信息系统（SVIS）由（U,A,V,f）组成，U为论域，A是属性的非空有限集合，(U,A∪{d},V,f)是集值信息决策系统（SVDIS），d代表了决策属性，A代表了条件属性，A∩{d}=∅，VA是条件属性的取值，Vd是决策属性的取值，V=VA∪Vd，f是V关于U×(A∪{d})上的函数。集值信息系统中的函数满足f:U×A→2VA，单值系统中函数满足f:U×{d}→Vd。

接下来，以2位审稿人审稿结果为例进行模型的阐释，数据如表1所示。

表1 中，G 代表了good，P 代表了poor，Ac 代表了accept，Re 代表了reject，{G,P}则代表了两位审稿人意见不一致，也就是集值信息。C={K1,K2,K3,K4}是U={1,2,3,4,5,6,7,8,9,10,11}的拟单层覆盖。其中K1={1,2,3,4,5,11}，K2={4,5,6,7,8}，K3={9,10,11}，K4={9}K10={1,2,3}，K20={6,7,8}，K30={10}，具体信息如图1所示。

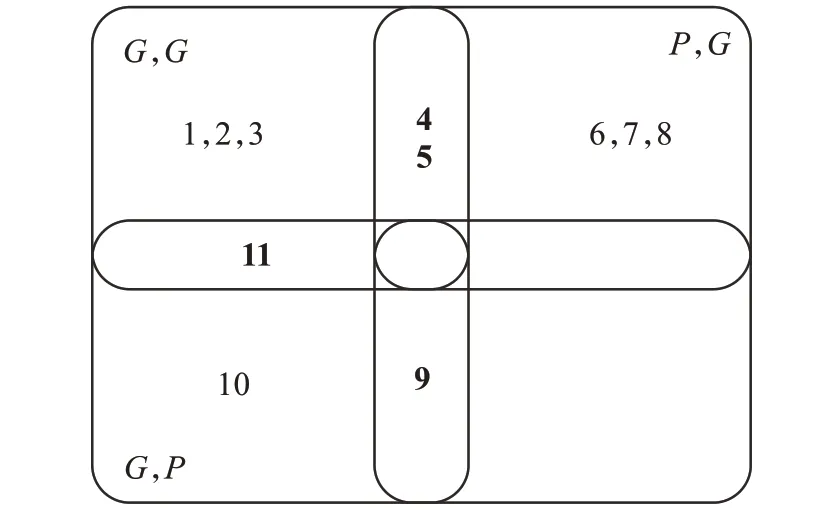
图1 拟单层覆盖Fig.1 Semi-monolayer covering

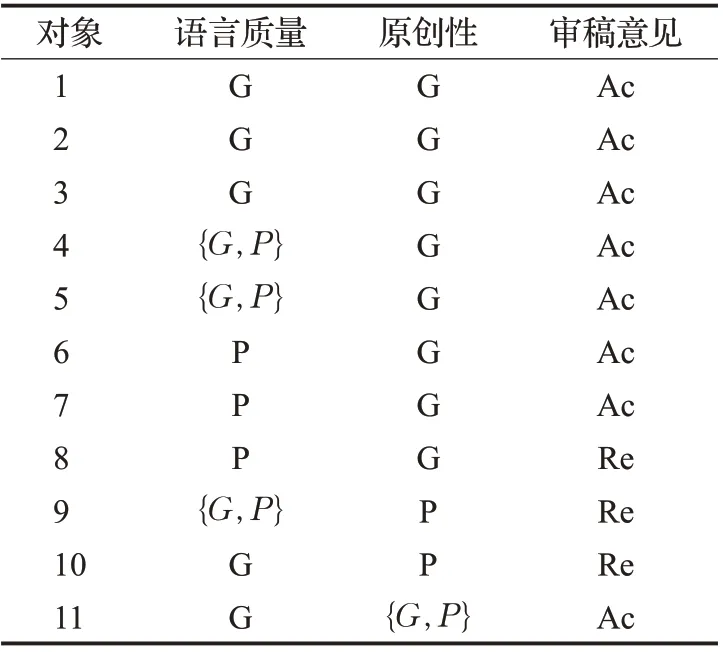
表1 集值信息系统Table 1 Set-valued information system

根据定义2，可以计算出不同决策集合的上下近似集合，如下所示：

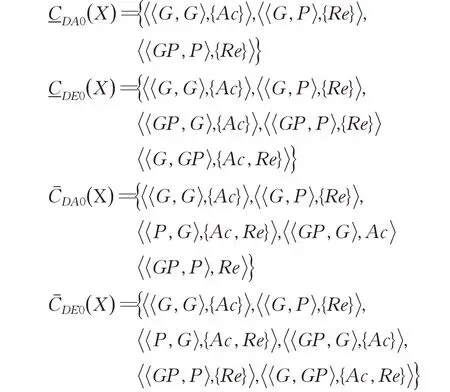
由于以上近似集求出的是决策规则，因此还需要通过决策规则来过滤数据，过滤出的数据如图2所示。

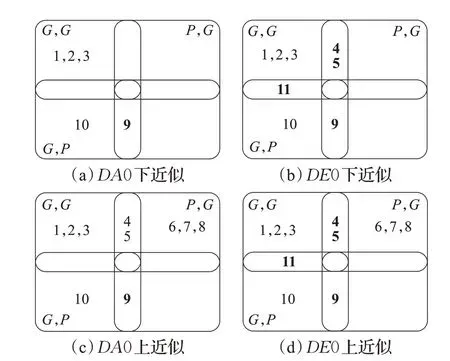
图2 近似集Fig.2 Approximation set

根据容差关系、非对称相似关系、限制性容差关系、最大相容类粗糙集相关定义，计算出其在表1中所对应的下近似集合为空，近似质量相对于拟单层覆盖粗集较低，在文献[19]中通过较为详细的实验证明了拟单层覆盖粗集相对于其他容差关系粗糙集近似质量高，因此选用拟单层覆盖粗集模型作为划分工具相对于其他容差关系粗糙集模型是有效且合理的，并在本文实验部分也给予了验证。

1.2 BorderlineSMOTE

BorderlineSMOTE[20]是一种基于SMOTE 的过采样改进算法。与SMOTE 不同，该算法只是用边界上的少数类来进行样本的人工合成。主要思想是将数据集中的少数类样本根据KNN原理划分为三类，分别是Safe、Danger、Noise。本文采用的方法是BorderlineSMOTE-1，仅在Danger类样本的k个近邻中，随机选取少数类样本进行人工生成数据，以增强Danger类数据的鲁棒性，算法步骤如下：

步骤1 根据不平衡率，计算出需要人工生成样本的数量S。

步骤2 对于少数类M中的每一个样本mi(i=1,2,…,n)计算其k个最近邻，记k个最近邻中多数类个数为k′( 0＜k′＜k)。

步骤3 对k′数量进行判断，如果k′=k，则该样本属于Noise 类样本，不做任何操作。如果k/2＞k′，则该样本属于Safe类样本，不做任何操作。如果k/2＜k′，则该样本属于Danger类样本，也就是边界上的样本，对其采取以下操作。

步骤4 计算Danger类中每个mi距M中其他少数类样本的n个最近邻。从n个最近邻中随机选取s个最近邻按照公式：

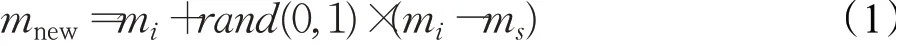
进行样本生成，mnew为新生成的样本，ms为随机选中的近邻样本。

重复步骤4，直至生成满足平衡率的S个样本。

1.3 ClusterCentroids

ClusterCentroids 最早由Singh 等[22]提出，是一种基于原型生成方式的高效欠采样方法，基于原始数据集Doriginal生成一个子集D′，D′的生成方式是基于k-Means算法求出Doriginal的簇心进行替换原始数据，而不是从Doriginal中进行选取，通过这种下采样方式能够很好地保证源数据的信息质量与信息载量，算法步骤如下：

步骤1 计算不平衡率，根据不平衡率计算需要聚类的个数k。

步骤2 在样本集Doriginal中随机选取k个多数类样本作为初始的簇中心。

步骤3 根据公式计算每个多数类样本与簇中心的距离，将距离近的多数类样本归为一类，形成新的簇。

步骤4 计算每个簇中对应坐标向量的平均值，从而求出新的簇心向量。

步骤5 重复步骤3 与步骤4，直至簇中心向量未更新。

步骤6 将生成的簇中心向量代替原有的多数类样本，加入到数据集中。

至此，通过簇心代替原有的多数类向量，对不平衡数据完成欠采样。

2 SMCRS-BS-CL

本章将对SMCRS-BS-CL算法原理进行介绍，并将该模型核心代码部分进行阐述。

2.1 SMCRS-BS-CL算法思想

由粗糙集的定义可知，粗糙集中下近似集中的元素是可靠且数据质量较高的，因此，选取下近似集中的决策规则作为知识提取是合理的。

从1.1 节中理论与结果可以看出，拟单层覆盖粗集相对于传统的覆盖粗糙集来说，对于每一个块都有一个全局且独特的标签，并且能将可靠元与争议元通过单值与集值建立一一对应的关系。除此之外，将所有的可靠元加入运算，并通过可靠元所对应的决策来对争议元的决策进行赋值，能够大大提升数据的数据质量。此外，拟单层覆盖粗集相较于其他容差关系粗糙集有较高的近似质量，在文献[19]中已经经过证实，较高的近似质量能够保证在对数据进行规则提取的同时极大程度地保留数据的完整性，以保证模型的泛化能力。

对于BorderlineSMOTE-1（BS）来说，为了提升分类算法能力，仅对边界域元素进行过采样，以提升整体分类精度。然而，原始数据集有可能会存在大量的噪声数据，用BS直接处理可能会降低分类效果。以1.1节中的例子来说，对象6、7、8 虽然且同为可靠元素，但其对应的决策并不相同，因此在进行下近似求解时，由于它的知识模糊表达性质并不会将其考虑进去，这样就能够降低因数据模糊而造成的影响。此外，对于集值数据，只有确定能与可靠元素建立规则的才予以保留，这样做，可以极大程度地确定信息表达的正确性。BS生成数据模拟如图3 所示，通过拟单层覆盖粗集下近似处理，能够提供给BS 更可靠的信息，降低信息表达不确定以及噪声数据对BS 的影响，并通过BS 生成更为可靠的数据，也就是图3中的黑色实心五角星的数据。

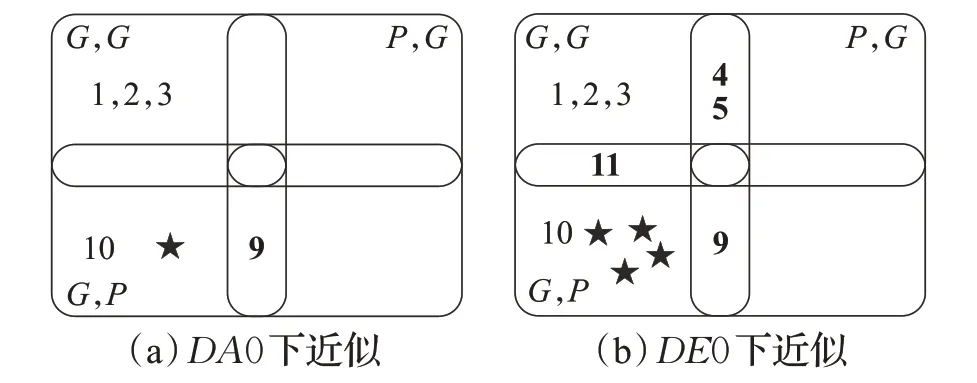
图3 BS生成数据模拟Fig.3 BS generates data simulation

对于ClusterCentroids（CL）来说，基于原型生成式的欠采样方法在一定程度上会将原有高质量数据抹去，降低分类精度。考虑到在不平衡数据中，少数类数据尤其珍贵，而下近似由于追求较好的数据质量可能会造成少数类数据被过滤掉，因此使用CL 算法对不满足下近似的数据质量较低的数据进行欠采样，如图4所示。通过CL 模型将多数类聚合，这样做首先避免了高质量数据在欠采样过程中被抹掉，其次还能保留少数类数据，并且对数据质量较低的多数类数据进行原型生成，降低噪声对整体数据分类能力的影响。

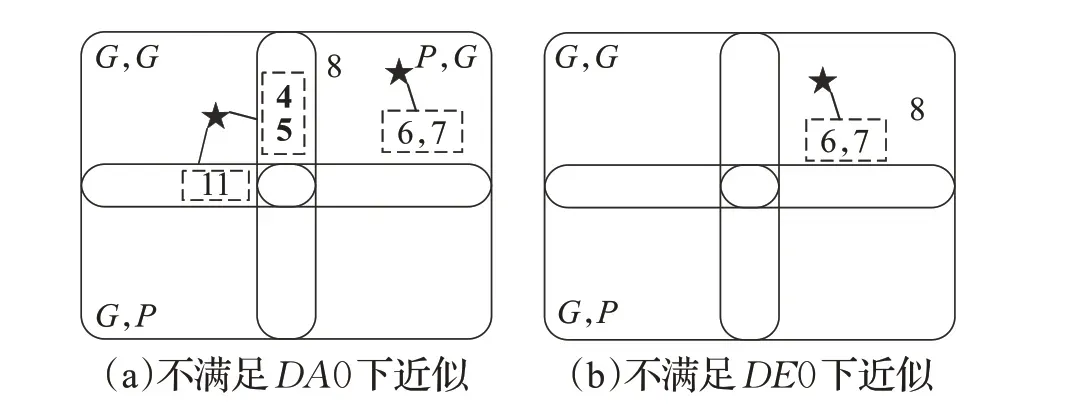
图4 CL欠采样数据模拟Fig.4 CL under-sampled data simulation

SMCRS-BS-CL模型是基于拟单层覆盖粗集的分治法预处理模型，它首先使用拟单层覆盖粗集就DA0 下近似与DE0下近似将不平衡数据分别划分为4个部分，分别为满足DA0下近似与不满足DA0下近似的数据，满足DE0下近似与不满足DE0下近似的数据。将满足下近似的数据用BS 进行过采样处理，增强边界域区分性的同时极大程度降低噪声数据对BS的影响。

此外，为了充分提取数据的知识表达信息，将不属于下近似的数据用CL 进行欠采样处理，目的也是降低噪声数据对整体数据集的影响。最后，将相对应处理好的数据集进行合并，具体流程如图5 所示。根据图5 思想，结合其他不平衡数据处理算法替代了BS与CL进行了对比实验，验证了SMCRS-BS-CL 的有效性，具体数据在实验部分展示。

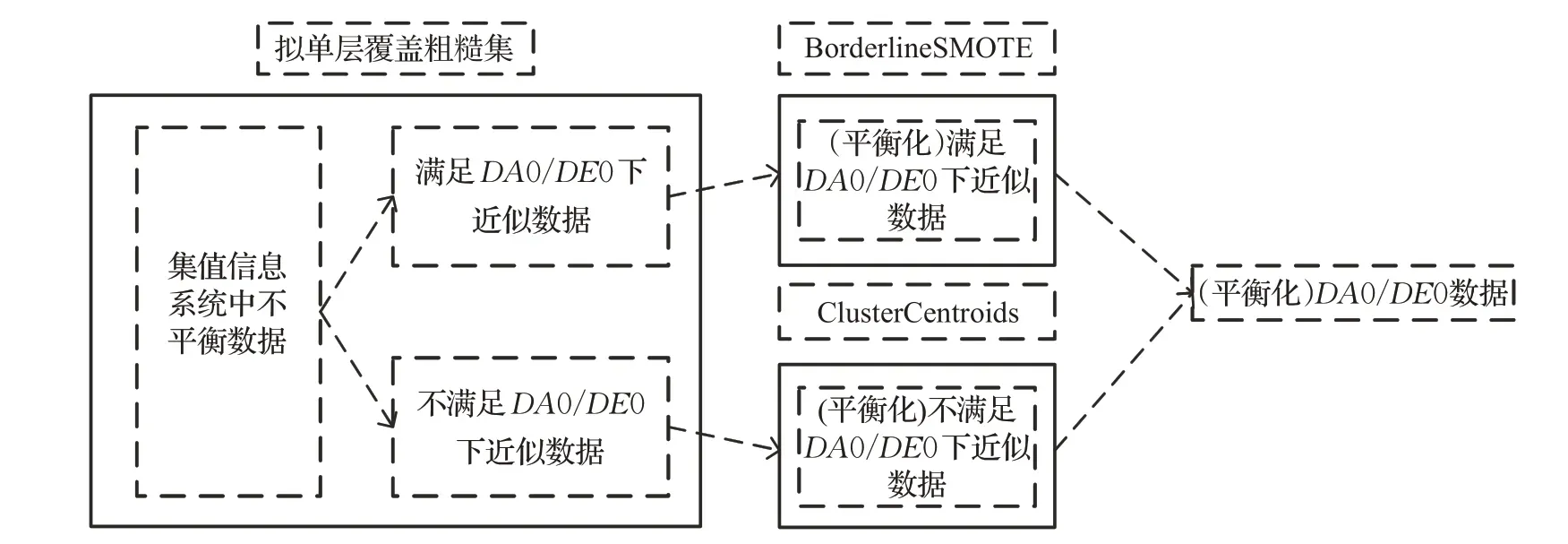
图5 SMCRS-BS-CL算法流程图Fig.5 Flow chart of SMCRS-BS-CL algorithm

2.2 SMCRS-BS-CL算法核心步骤

SMCRS-BS-CL模型的算法核心即拟单层覆盖粗集的实现过程，具体可分为如下步骤：

步骤1 输入数据，构建集值信息决策系统ISVDS=(U,A∪{d},V,f)。

步骤2 根据定义1计算覆盖块K以及相对应的K0。

步骤3 根据步骤2 中计算出的K、K0，求出不同决策集对应的决策规则（定义2），并将求出的结果取并集，得到不同近似集的整体决策规则。

步骤4 根据步骤3计算出的决策规则，对原始数据进行决策过滤，选取数据质量较高的数据。

步骤5 调用BS算法，根据步骤4中计算出的DA0、DE0 下近似进行过采样。

步骤6 调用CL 算法，根据步骤4 中计算出的不满足DA0、DE0下近似的样本进行欠采样。

步骤7 合并步骤5 与步骤6 中的数据，完成集值数据的数据处理。通过以上步骤，完成SMCRS-BS-CL算法的整个过程。

SMCRS-BS-CL算法对拟单层覆盖粗集进行了下一步的研究，由近似质量转为了决策规则的提取，通过计算出决策规则，结合数据进行性数据清洗，筛选出符合决策规则的高质量数据。其次，结合BS 与CL 算法，通过分治法提升数据质量与降低数据损耗来提升不平衡数据的分类能力。

3 实验

实验中的数据集来自Kaggle中的不平衡数据集，选取了Abalone、Bank、Waktu、Magic、Wdbc、White_wine和House_vote共7个不同数据集，并将数据集划分为训练集与测试集，比例为8∶2。其中前6个数据集是完备的，在进行拟单层覆盖粗集算法时首先构建集值信息系统，转变为集值数据，实现方式由3.1 节给出。House_vote数据集是不完备的，直接根据映射关系将缺失值映射为集值进行处理，此外，为了加大数据的不平衡性，对House_vote数据集少数类进行随机抽取处理，使其平衡率为3∶1，具体信息如表2所示。

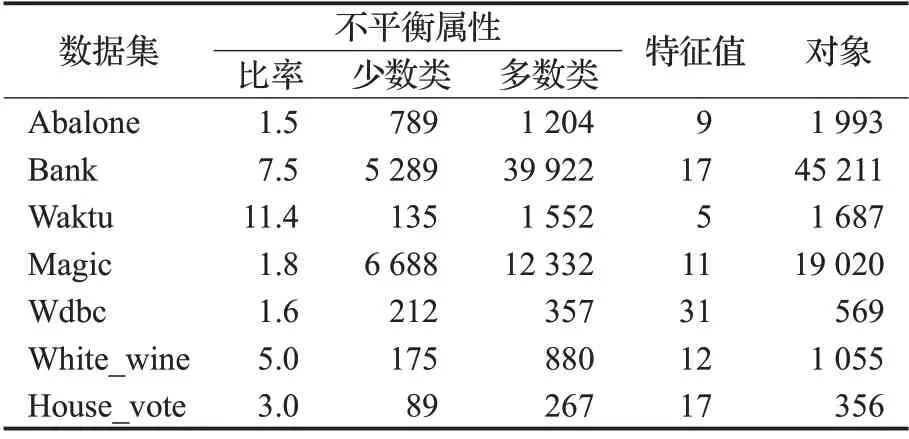
表2 数据集Table 2 Datasets

本次实验采用Python 3.6进行实验设计，实验过程中，SMOTE[23]、BorderlineSMOTE-1、BorderlineSMOTE-2[20]过采样方法的过采样率为100%，即平衡少数类样本与多数类样本的个数，近邻个数设置为5，ClusterCentroids、TomekLinks[24]欠采样率均为100%，即平衡少数类样本与多数类样本的个数。其中ClusterCentroids 聚类的簇数由不平衡率进行确定，各个分类算法与不平衡数据处理方法的随机种子设置为42，指标评测值是进行10次实验计算平均值得出的结果。

3.1 集值信息系统构造

集值信息系统覆盖规则的构建就是计算出每列属性的最小值、最大值、均值、中位数。判断每个对象属性值所属的区间位置，如果位于最小值与min{均值，中位数}之间或是位于max{均值，中位数}与最大值之间，则该属性值被认为是单值；若属性值位于中位数与均值之间，则该属性值被认为是集值。

3.2 分类能力评价指标

由于不平衡数据本身的独特性质，仅用单一指标去评价不平衡数据并不能有效地展示其分类性能。因此，选取F-score、AUC、Accuracy 作为不平衡数据的分类效果评价指标。

基于表3，可以算出F-score（公式（3））、AUC（公式（4））、Accuracy（公式（5））计算过程中的指标。

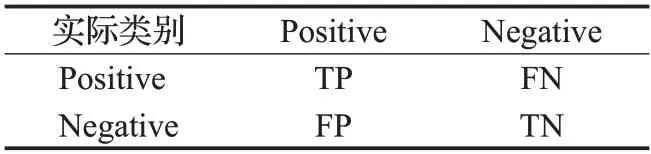
表3 混淆矩阵Table 3 Confusion matrix

其中，FPR、TPR分别代表了假阳性率与真阳性率，二者与坐标轴围成的面积即为AUC值。

3.3 对比实验

为了检测SMCRS-BS-CL 算法对不平衡数据分类性能的提升，选取了SMOTE、BorderlineSMOTE-1、BorderlineSMOTE-2、ClusterCentroids、TomekLinks、SMOTETomek分别对数据集进行处理，设计了如下对比实验方案，在实验数据表中，加粗的数据为最优值，加下划线的数据为次优值。SMCRS-BS-CC-DE0与SMCRSBS-CC-DA0分别代表了经过DE0近似集与DA0近似集按照本文模型处理后的结果。

3.3.1 F-score

为了验证SMCRS-BS-CL 模型相较于其他不平衡数据处理模型的组合效果，结合图中思想，将BS（BS-CL）模型更换为SMOTE（SMOTE-CL）、BorderlineSMOTE-2（BS-2-CL），将CL 模型更换为Tomek（BS-Tomek）。此外，为了验证CL 模型的重要性，单独将BS 模型处理后的数据用于验证，分类器采用Extra-Tree[25]，评价指标选取F-score，具体数值如表4所示。以模型整体效果为标准，SMCRS-BS-CL 模型在5 个数据集合上都有较好的效果，验证了该模型的有效性。

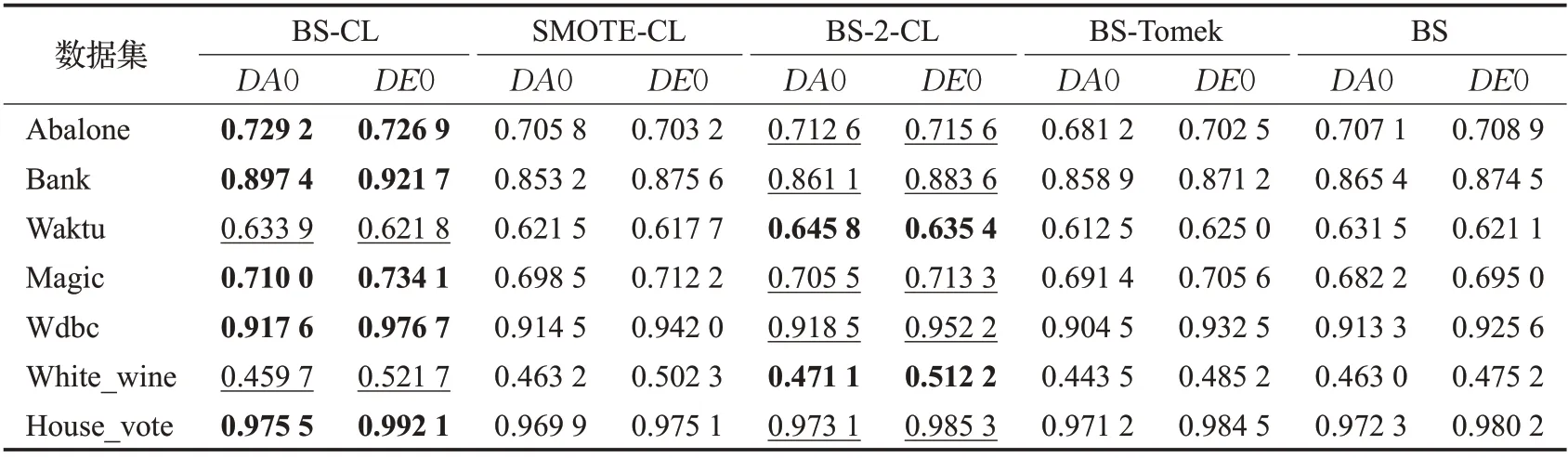
表4 不同组合模型F-score对比Table 4 Comparison of F-scores for different combination models

将SMCRS-BS-CL 与其他不平衡数据处理方法处理后的数据经过Extratree分类器训练后的F-score值如表5 所示。从表5 中可以看出，SMCRS-BS-CC-DE0 较原始数据集F-score 平均提升4.30 个百分点，SMCRSBS-CC-DA0平均提升了1.85个百分点。SMCRS-BS-CL相对其他方法表现较好。

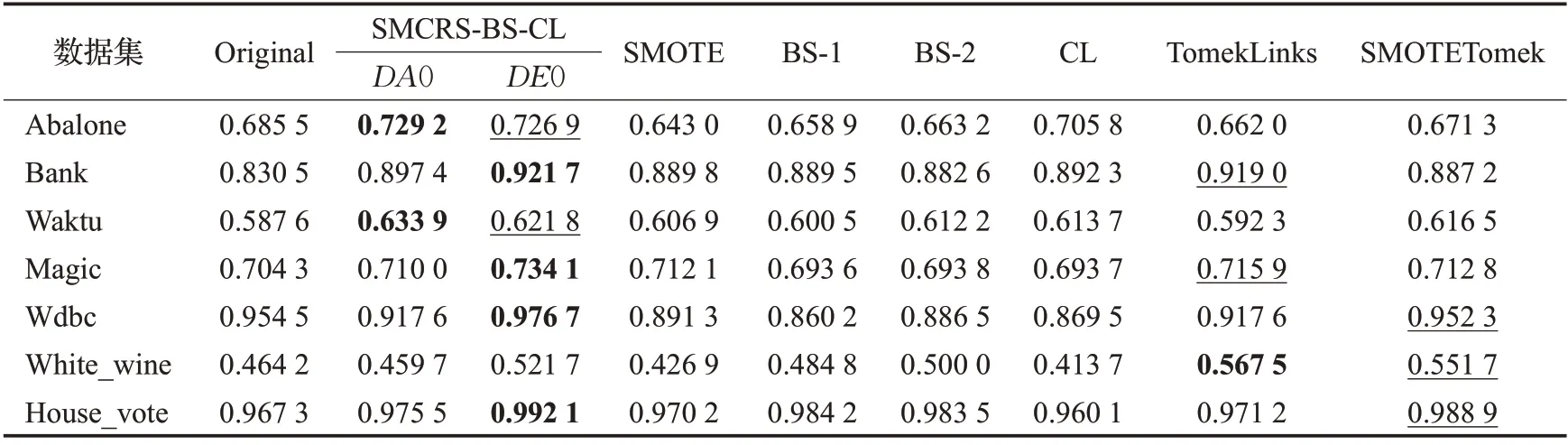
表5 不同模型F-score值Table 5 F-scores for different combination models

3.3.2 AUC

首先，通过ExtraTree 与DecisionTree[26]作为分类器（随机种子设置为42，其余参数均是默认值，下同），训练经过SMCRS-BS-CL 以及上述不平衡数据算法处理过的数据，得到每个处理方式处理后的所对应的AUC值。

ExtraTree分类器对应的AUC值如图6所示。

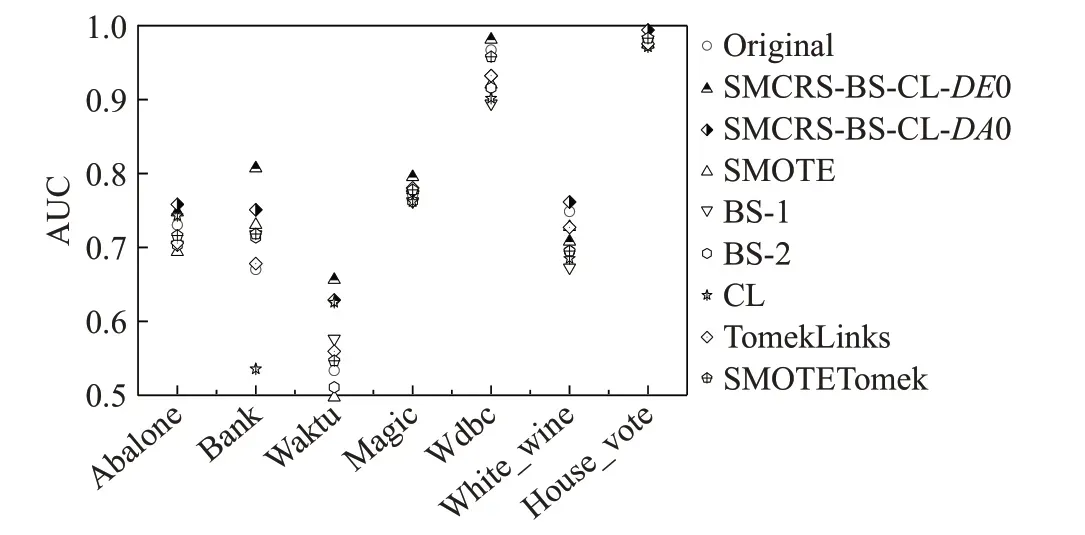
图6 ExtraTree下AUC值比较Fig.6 Comparison of AUC values under ExtraTree

从图6中可以看出，SMCRS-BS-CL整体较其他方法表现好。具体数值如表6，根据表6 可以看出SMCRSBS-CL-DE0 在5 个数据集上达到了最优值，AUC 值平均提升了4.22 个百分点。SMCRS-BS-CL-DA0 在两个数据集上达到了最大值，较原始数据集平均提升了2.71个百分点。但SMCRS-BS-CL-DE0 在White_wine 数据集表现一般，原因是由于构建集值信息系统过程中，争议元较多，使用DA0近似集对数据集进行决策过滤能够更好清除噪声数据从而达到更好的效果。整体来说，SMCRS-BS-CL-DE0表现较SMCRS-BS-CL-DA0优异。

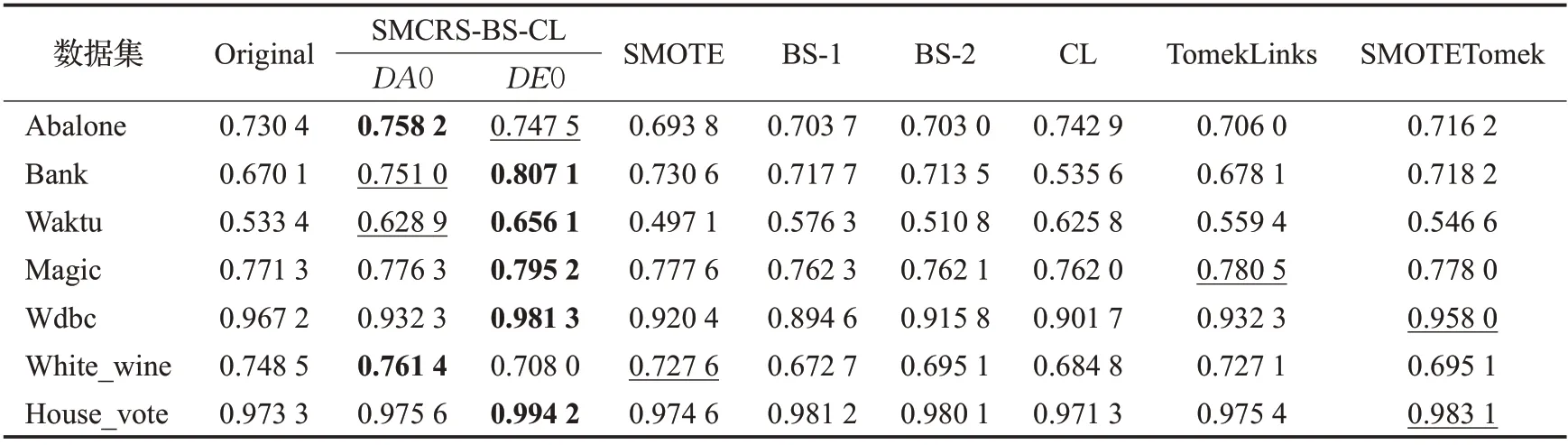
表6 ExtraTree下AUC值Table 6 AUC values under ExtraTree

DecisionTree分类器对应的AUC值如表7所示。根据表7中数据可以得到SMCRS-BS-CL-DE0在3个数据集上达到了最优，两个数据集达到了次优，AUC值平均提升了3.10 个百分点。SMCRS-BS-CL-DA0 在两个数据集上达到了最优，一个数据集达到了次优，原始数据集合平均提升了3.35 个百分点。整体来说，SMCRSBS-CL算法相对于其他算法表现优异。

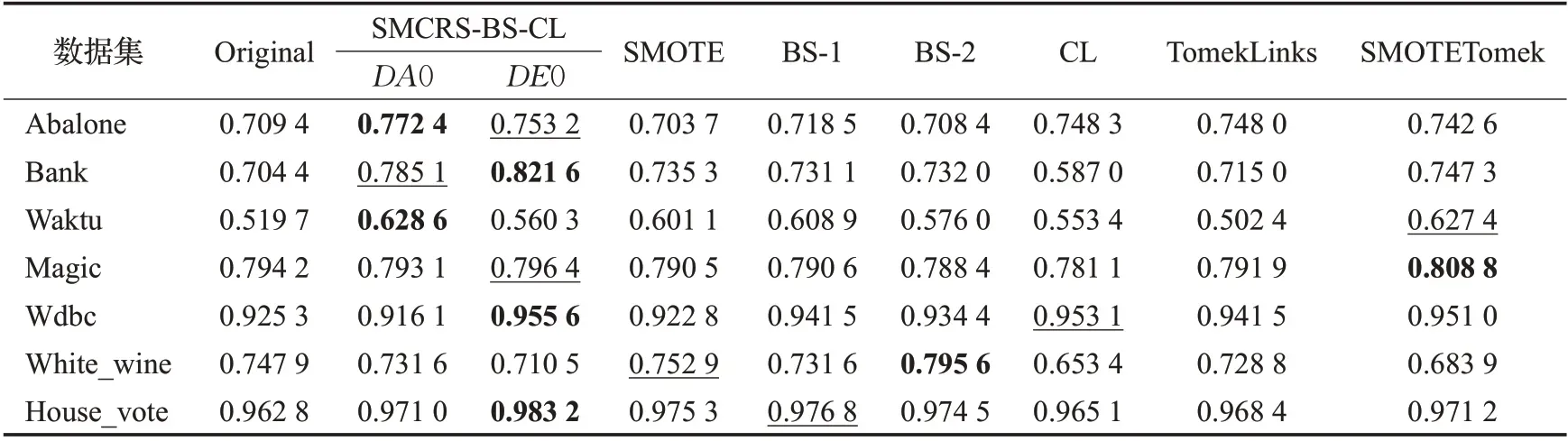
表7 DecisionTree下AUC值Table 7 AUC values under DecisionTree

3.3.3 Accuracy

为了验证拟单层覆盖粗集模型相对于其他容差关系模型的在集值信息系统中的优越性，本文采用容差关系粗糙集（TR）、限制性容差关系粗糙集（LTR）、非对称限制关系粗糙集（NTR）、最大相容类粗糙集（MTR）进行对比，对不平衡数据处理方式均是将属于下近似的数据进行过采样，不属于下近似的欠采样，最后将二者合并为一个数据集。训练器采用feature generation by convolutional neural network（FGCNN）[27]，该训练器是一种利用卷积神经网络进行自动特征提取的深度学习模型，模型中epochs设置为50。经过FGCNN训练后的Accuracy如图7所示，从图7中明显看出SMCRS-BS-CL相对于其他容差关系粗糙集模型，在大多数数据集上表现出了较好的结果。

4 结束语

针对集值信息系统中的不平衡数据问题，本文提出了一种基于拟单层覆盖粗集与BorderlineSMOTE、ClusterCentroids 的混合采样方法。该方法首先通过拟单层覆盖粗集分别用DE0 与DA0 下近似进行数据划分，将属于下近似的数据用BorderlineSMOTE进行过采样，将不属于下近似的数据用ClusterCentroids进行欠采样，最后分别将属于DE0 与DA0 的过采样数据与欠采样数据合并，达到对不平衡数据的预处理。这种处理方式能够极大程度地增强边界数据可区分性，并且能够降低少数类数据的信息损耗。最后，基于Kaggle上的公开数据集进行实验验证，证明了算法的有效性。但是该算法仍有需要改进的地方，由于结合了多种算法，模型处理上稍微复杂，仍需要进一步深入优化。