三支面向属性概念格的规则提取

贺晓丽，柳战英，钱 婷

1.西安石油大学 理学院，西安 710065

2.西北大学 概念认知与智能研究中心，西安 710127

3.西安石油大学 计算机学院，西安 710065

形式概念分析是德国数学家Wille[1]于1982 年提出的一种数据分析理论，其中形式概念与概念格是形式概念分析的基础。作为数据分析和知识处理的一种有效工具，形式概念分析在数据挖掘、机器学习和信息检索等领域有着广泛的应用。

形式概念分析与其他理论相结合，产生了一系列概念格的模型。Duntsch和Gediga[2]把粗糙集中的上、下近似引入到形式概念分析之中，提出了面向属性的形式概念。类似地，Yao[3]给出了面向对象概念的定义并研究了它的一些性质。针对部分对象属性值缺失这一现象，Burmeister等[4]进一步提出了不完备形式背景，并研究了基于不完备信息的概念分析及知识获取。Li等[5]在不完备形式背景中定义了近似概念并研究了近似概念格的构造、规则提取与属性约简。Belohlavek[6]定义了一对模糊伽罗瓦连接并研究了相应的性质，进而给出模糊概念的刻画。与三支决策思想相结合，祁建军等提出了三支概念格，进一步研究对象（属性）诱导的三支概念格与经典概念格之间的联系[7-8]。Qian等[9]通过将原背景与其补背景并置（叠置）给出三支概念格的构造。刘琳等[10-11]给出了属性（对象）导出三支概念格的规则提取的方法，并研究了所获的规则与经典形式背景下规则的内在联系。Wei等[12]利用置信度探讨了属性导出三支概念格的规则提取方法和非冗余规则的性质。王一宾等[13]通过合并对象导出三支概念格和属性导出三支概念格，给出相应的规则提取算法。Ren等[14]探讨了三支概念格的四种约简理论。Li 等[15]基于不完备形式背景研究了三支近似概念的约简理论。而三支概念刻画了对象和属性之间的“共同具有”和“共同不具有”关系，为了刻画对象和属性之间的“局部完全共有”和“局部完全不共有”的关系，Wei和Qian[16-17]提出了三支面向属性（对象）概念，并给出了三支面向属性（对象）概念格的构造方法。

规则提取是形式概念分析的主要目的之一，也是该领域的重要研究课题。近年来，已有一系列相关研究成果。例如，张文修等[18]将决策规则的概念引入到形式概念分析之中。为了提升决策规则对于决策分析的有效性，Li 等[19-20]提出了一种从形式背景之中获取所有非冗余决策规则的方法和知识约简理论。Qu等[21]首次引入了决策形式背景中的决策蕴涵。Wu等[22]细致研究了形式背景中的粒规则。Ren等[23]通过使用面向属性和面向对象的概念格，提出了两种不同的决策规则。然而，基于基于由面向属性概念和面向对象概念所导出决策规则的属性约简还没有得到深入研究，Qin 等[24]在此方面做了较为深入的研究，得到了诸多有趣的结论。已有这些研究对基于三支面向属性概念格的决策规则未有涉及，而三支面向属性概念刻画了对象和属性之间的“局部完全共有”和“局部不完全共有”关系，相应的决策规则语义更为丰富，表达更为精细。本文正是鉴于此考虑，在文献[16-17]基础上，首先给出决策形式背景的两种协调性的定义（P-协调和AEP-协调），进一步探讨了两种协调性之间的联系；其次，研究了三支面向属性概念格的规则提取方法和非冗余规则的刻画，并给出获取三支面向属性概念非冗余规则的算法；最后，从原背景和补背景两种角度，讨论了三支面向属性规则与面向属性规则之间的内在联系。

1 基础知识

定义1[2-3]设(U,A,I)为一形式背景，且2U与2A之间的一对算子定义如下：对于任意的X⊆U,B⊆A：

称LP(U,A,I)为(U,A,I)的面向属性概念格。

例1 表1是一个形式背景(U,A,I)，对象集U={1,2,3,4,5}，条件属性集A={a,b,c,d,e}，该背景的面向属性概念格LP(U,A,I)如图1所示。

图1 面向属性概念格LP(U,A,I)Fig.1 Property oriented concept lattice LP(U,A,I)

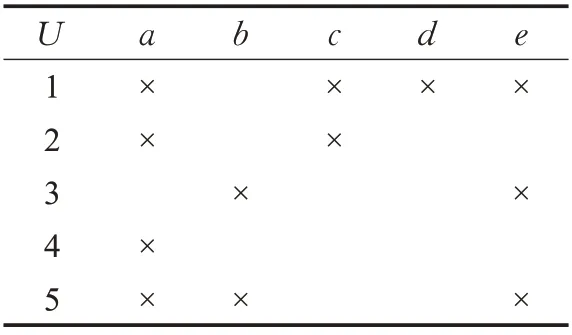
表1 形式背景(U,A,I)Table 1 Formal context(U,A,I)

可以将上述定义的算子推广为一对负算子。

定义2 设(U,A,I)为一形式背景，且2U与2A之间的一对负算子定义如下：

对于任意的X⊆U,B⊆A：

定义4[16]设(U,A,I)为一形式背景，∀X,Y⊆U且B⊆A，由属性诱导的三支面向属性算子分别定义如下：⊳:2A→2U×2U，⊲:2U×2U→2A，其中B⊳=(B□,B-□)且(X,Y)⊲=X⋄∪Y⋄。

若B⊳=(X,Y),(X,Y)⊲=B，则称((X,Y),B)为由属性诱导的三支面向属性概念。(U,A,I)上所有的三支面向属性概念构成之集为LAEP(U,A,I)。在LAEP(U,A,I)上定义二元关系“≤”如下：对于任意的((X,Y),B),((Z,W),C)∈LAEP(U,A,I),((X,Y),B)≤((Z,W),C)⇔X⊆Z且Y⊆W⇔B⊆C，不难验证≤为偏序关系且(LAEP(U,A,I),≤)构成一个完备格，称LAEP(U,A,I)为三支面向属性概念格。

任意两个三支面向属性概念((X,Y),B)，((Z,W),C)的上确界和下确界为：

((X,Y),B)∨((Z,W),C)=(((X,Y)∪(Z,W))⊲⊳,B∪C)

((X,Y),B)∧((Z,W),C)=((X,Y)∩(Z,W),(B∩C)⊳⊲)

将三支决策思想与面向属性概念结合可以得到三支面向属性概念，三支面向属性概念可以精确的刻画局部完全共有与局部完全不共有的含义。

引理1[17]设(U,A,I)为一形式背景，(U,A,Ic)为其补背景，其中Ic=(U×A)I，若(X,B)∈LP(U,A,I)及(Y,C)∈LP(U,A,Ic)，则((X,B-□),B)∈LAEP(U,A,I)且((C□,Y),C)∈LAEP(U,A,I)。

引理2[17]设(U,A,I)为一形式背景，(U,A,Ic)为其补背景，其中xIc=(U×A)×I，若((X,Y),B)∈LAEP(U,A,I)，则(X,X⋄)∈LP(U,A,I)且(Y,Y⋄)∈LP(U,A,Ic)。

引理3[17]设(U,A,I)为一形式背景，(U,A,Ic)为其补背景，其中Ic=(U×A)I，则：

（1）存在LP(U,A,I)到LAEP(U,A,I)的保并序嵌入；（2）存在LP(U,A,Ic)到LAEP(U,A,I)的保并序嵌入。

2 三支面向属性概念格的规则提取

下面给出三支面向属性概念的AEP-协调性、AEP-规则和相应的非冗余规则的定义。

定义5 设(U,A,I,D,J) 是一个决策形式背景，LAEP(U,A,I)和LAEP(U,D,J)分别为由条件属性和决策属性导出的三支面向属性概念格，若对于任意的((Z,W),C)∈LAEP(U,D,J)，存在((X,Y),B)∈LAEP(U,A,I)，使得(X,Y)=(Z,W)（即，X=Z,Y=W），则称LAEP(U,A,I)细于LAEP(U,D,J)，记为：

LAEP(U,A,I)≤LAEP(U,D,J)

相应地，称形式背景(U,A,I,D,J)是三支面向属性协调的，简称AEP-协调的。

例2 表2 是一决策形式背景(U,A,I,D,J)，对象集U={1,2,3,4}，条件属性集A={a,b,c,d,e,f}，决策属性集D={g,h,k}，该背景的三支面向属性概念格LAEP(U,A,I)和LAEP(U,D,J)分别如图2和图3所示，显然LAEP(U,A,I)≤LAEP(U,D,J)。

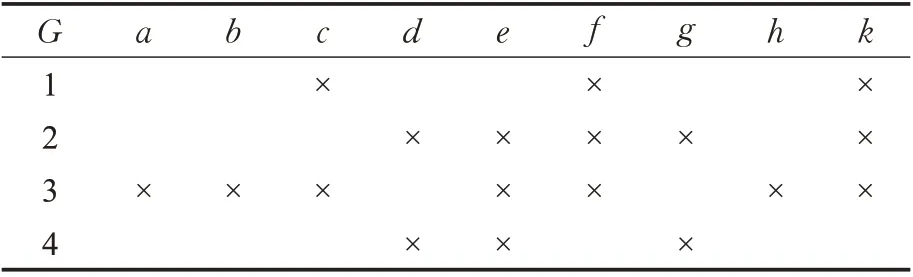
表2 决策形式背景(U,A,I,D,J)Table 2 Decision formal context(U,A,I,D,J)

图2 三支面向属性概念格LAEP(U,A,I)Fig.2 Three-way property oriented concept lattice LAEP(U,A,I)

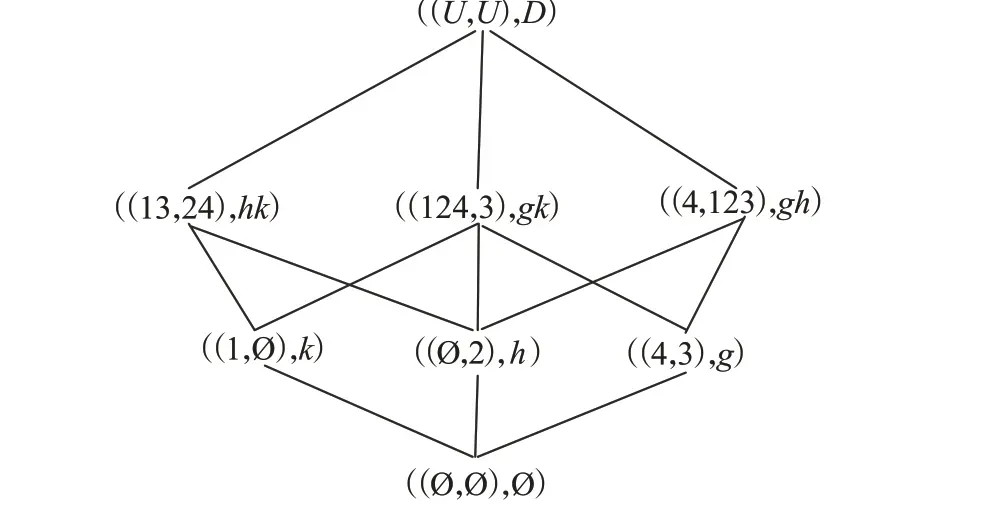
图3 三支面向属性概念格LAEP(U,D,J)Fig.3 Three-way property oriented concept lattice LAEP(U,D,J)

定义6 设(U,A,I,D,J)是AEP-协调的决策形式背景，若对于(X,Y),(Z,W)≠(∅,∅),(U,U)，((X,Y),B)∈LAEP(U,A,I)，((Z,W),C)∈LAEP(U,D,J)，满足(X,Y)⊆(Z,W)（即，X⊆Z,Y⊆W），则称B→C是一个三支面向属性决策规则，简称为AEP-规则，记为IfB，thenC。以下用ℜAEP表示决策形式背景(U,A,I,D,J)上所有的AEP-规则的集合。

由B⊳=(X,Y)⊆(Z,W)=C⊳知，对于任意的(x,y)∈(X,Y)，如果x局部完全共有属性集B，则x局部完全共有属性集C；且y局部不完全共有属性集B，则y局部不完全共有属性集C。三支面向属性概念格比面向概念格蕴含的信息多，不仅反映了对象局部完全共有的属性，而且也能反映对象局部不完全共有的属性，因此，所定义的三支面向属性决策规则不仅给出规则的正信息，而且给出了规则的负信息，使得所获取的规则语义更加丰富。

定义7 设决策形式背景(U,A,I,D,J)是AEP-协调的，对于任意两个三支面向属性决策规则B→C和B′→C′，若其满足条件B⊇B′,C′⊇C，则称规则B→C蕴含规则B′→C′，记B→C⇒B′→C′，并称规则B′→C′是冗余的。

定理1 设(U,A,I,D,J)为一决策形式背景，((X,Y),B)∈LAEP(U,A,I) ，((Z,W),C)∈LAEP(U,D,J) ，B→C∈ℜAEP，则B→C是冗余的当且仅当αP((X,Y),(Z,W))=0或βP((X,Y),(Z,W))=0；则B→C是非冗余的当且仅当αP((X,Y),(Z,W))=1 且βP((X,Y),(Z,W))=1。

例3（续例2）决策形式背景(U,A,I,D,J)的三支面向属性规则之集ℜAEP和相应的非冗余规则之集ℜ*AEP如表3所示。

表3 三支面向属性规则之集ℜAEP 和非冗余规则之集ℜ*AEPTable 3 Three-way property rules ℜAEP and non-redundant three-way rules ℜ*AEP

下面研究三支面向属性概念格与面向属性概念格的规则之间的内在联系。

定义8 设(U,A,I,D,J)是一个决策形式背景，∀(Y,C)∈LP(U,D,J)，∃(X,B)∈LP(U,A,I)，使得X⊆Y，则称LP(U,A,I)细于LP(U,D,J)，记作LP(U,A,I)≤LP(U,D,J)，简称决策形式背景(U,A,I,D,J)是P-协调的。

定义9 设(U,A,I,D,J)是一个决策形式背景，且满足LP(U,A,I)≤LP(U,D,J)，如果对于(X,B)∈LP(U,A,I)，存在(Y,C)∈LP(U,D,J)，满足X⊆Y（其中，X≠∅且Y≠U），则称B→C为一面向属性规则，所有面向属性规则之集记为ℜP。

这个定理说明在面向属性概念规则中，可以找到更少的规则。

例4 表2的面向属性概念格LP(U,A,I)和LP(U,D,J)分别如图4和5所示，显然LP(U,A,I)≤LP(U,D,J)，表4给出了形式背景(U,A,I,D,J)的面向属性规则，容易验证ℜP⊆ℜAEP。

图4 面向属性概念格LP(U,A,I)Fig.4 Property oriented concept lattice LP(U,A,I)

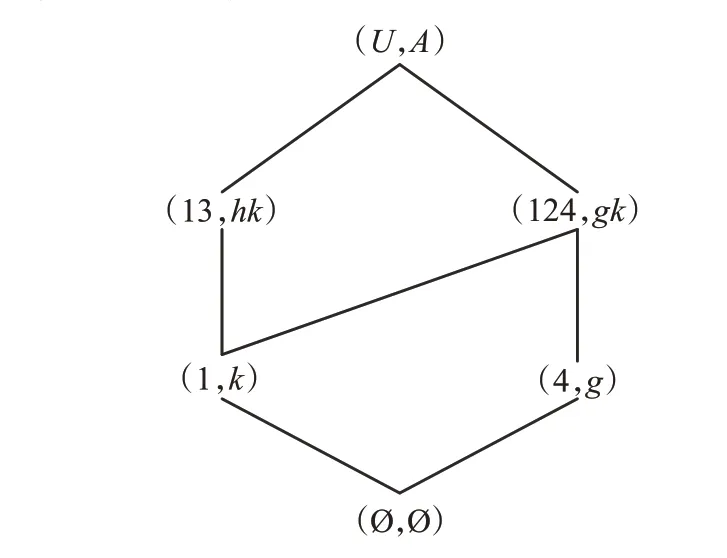
图5 面向属性概念格LP(U,D,J)Fig.5 Property oriented conceptlattice LP(U,D,J)

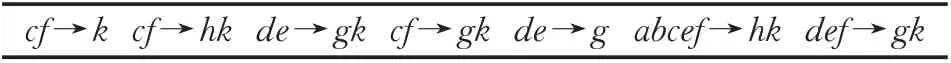
表4 形式背景(U,A,I,D,J)的面向属性规则集ℜPTable 4 Property oriented rules ℜP of formal context (U,A,I,D,J)

3 基于决策形式背景的补背景的两种属性规则的比较

在本章中，基于决策形式背景的补背景，进一步研究了面向属性规则和三支面向属性规则之间的区别与联系，探讨了规则提取与背景协调性之间的内在联系。

所以，LP(U,A,Ic)≤LP(U,D,Jc)。

定理7 设(U,A,I,D,J) 是一个决策形式背景，且LAEP(U,A,I)≤LAEP(U,D,J)，对于任意的B1→C∈ℜcP，总存在B2→C∈ℜAEP满足B1⊆B2。

4 总结与展望

将三支决策思想引入到面向属性概念格中，得到三支面向属性概念格，在细于关系下定义了三支面向属性的规则和相应的冗余规则并给出非冗余规则的刻画和算法；其次，研究面向属性规则与三支面向属性规则之间的内在联系及协调性之间的关系，最后，在决策形式背景的补背景中，得到相应的三支面向属性概念规则，可以丰富三支面向属性概念规则的获取理论。本文只考虑协调性下的三支面向属性规则提取，还可以进一步考虑非协调下的三支面向属性规则获取的方法及三支面向对象规则获取的方法和联系。