多策略黑猩猩优化算法研究及其工程应用

黄 倩，刘 升，李萌萌，郭雨鑫

上海工程技术大学 管理学院，上海 201620

黑猩猩优化算法（chimp optimization algorithm，COA）是由Khishe和Mosavi[1]于2020年提出的一种启发式优化算法。作为一种新型的进化算法，相比于其他群智能算法，COA 除了参数少、易于理解之外，还拥有最重要的两大特点：一是将种群划分成独立个体，模拟其狩猎时的分工行为，而个体的多样性可以使算法更加彻底的搜索空间以提高算法的勘探能力；二是引入混沌因子来代表黑猩猩在围猎过程中受到群体激励而带来的个体混乱捕猎行为，从而提高了算法在开发阶段的收敛速度。

在研究中发现，黑猩猩优化算法（COA）与鲸鱼优化算法（WOA）、灰狼优化算法（GWO）的运行原理有一定相通性，但其在收敛精度和收敛速度上又明显优于两个算法，因而对黑猩猩优化算法的改进具有很高的研究价值。基本的启发式优化算法普遍具有易陷入局部最优和收敛精度不高的问题，对此，众多学者在此类算法的改进策略研究对黑猩猩优化算法在寻优精度和收敛速度上的提升有一定借鉴意义。肖子雅等[2]提出一种基于精英反向学习策略和黄金正弦算法的改进WOA 算法（EGolden-SWOA），在寻优精度上提高了原始算法的性能，但收敛速度上仍有进步的空间。顾清华等[3]提出了一种基于遗传算法的改进GWO 算法，在提高全局收敛性和收敛精度上取得极大成果。Mohammad等[4]提出了一种基于维度学习的狩猎搜索策略的改进GWO 算法（IGWO），在增强种群多样性和平衡算法局部和全局搜索上基础上增强算法的开发能力，但在收敛过程中仍容易陷入局部最优。徐辰华等[5]提出一种将混沌理论与灰狼优化算法结合的Cat 混沌与高斯变异的改进灰狼优化算法，证明了混沌理论在提高算法收敛速度上突出表现。

尽管上述学者在算法的改进中取得了一定成果，但在如何平衡收敛精度和收敛速度上仍有一定不足，因此本文提出一种多策略黑猩猩优化算法（EOSMICOA）。运用无限折叠迭代混沌映射改进精英反向学习策略初始化种群，增加种群的多样性；利用单纯形法提高算法在局部搜索时跳出局部最小值的寻优能力；引入群个体记忆机制提高算法的寻优速度和精确度。通过20个测试函数实验对比，结果表明，无论在低维和高维实验，EOSMICOA 在全局寻优的精度以及收敛速度上都表现优秀。最后，通过将EOSMICOA、EGolden-SWOA 与CPSOGSA[6]改进算法应用于焊接梁的复杂工程优化问题上，结果证明EOSMICOA 能更有效地应用于工程实际问题中。

1 黑猩猩优化算法

在黑猩猩群落中，根据个体在狩猎过程中所显现出的智力和能力的多样化，对黑猩猩群分类为：驱赶者（Driver）、阻拦者（Barrier）、追捕者（Chaser）和攻击者（Attacker）。每一类黑猩猩都有自己的独立思考能力，并用自己的搜索策略探索和预测猎物的位置，他们拥有各自任务的同时，还会由于受到获得性行为和好处的社会激励使他们在狩猎的最后阶段会出现混乱个体捕猎行为。

黑猩猩优化算法的基本过程如下：假设有N只黑猩猩，第i只黑猩猩的位置为Xi，群体最优解为XAttacker，次优解为XBarrier，第三最优解为XChaser，第四最优解为XDriver。

首先描述黑猩猩接近并包围猎物的行为，其位置更新公式如下：

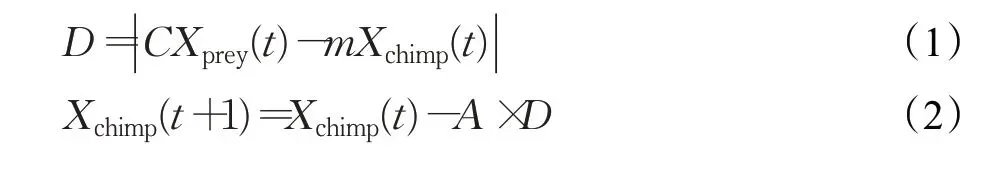
2 多策略黑猩猩优化算法

2.1 混沌反向学习策略初始化种群

由于启发式优化算法多存在过度依赖种群初始位置的问题，而以随机方式初始种群会使其分布不均匀，影响算法的求解精度。为此，本文提出一种基于无限折叠迭代混沌映射（Iteration映射）和精英反向学习混合的混沌反向学习策略来对种群初始化，以增加种群的多样性和质量。混沌运动具有遍历性和不重复性等特点，所以大多被学者用来生成种群的初始位置，而文献[7-10]中大多使用的是Logistic映射和Tent映射。通过图1的4个混沌映射对比，可以发现在1 000次迭代下，Logistic映射生成的混沌变量具有一定的双峰分布特征，在混沌吸引域的中间分布较为均匀，而两端分布较为稠密；Tent 映射在0～0.2 的取值范围内存在小周期现象、容易陷入不动点的问题；Sine映射和Logistic映射类似，在接近0 的底端也存在着分布相对稠密的问题；而相比之下，Iteration映射在0～1的分布最为均匀。为此，本文采用Iteration混沌映射。

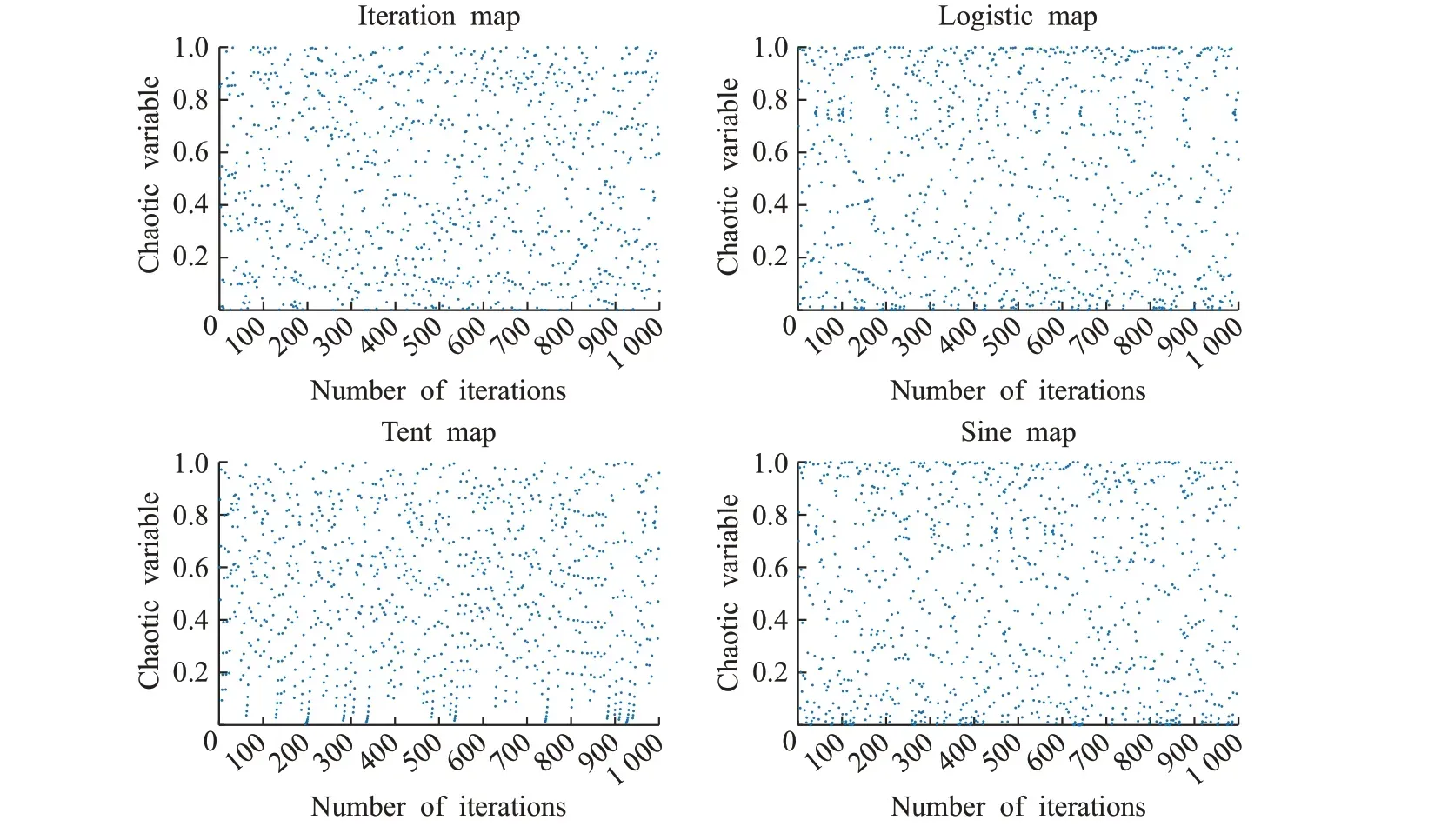
图1 混沌映射Fig.1 Chaotic map

Iteration映射数学表达式如下：

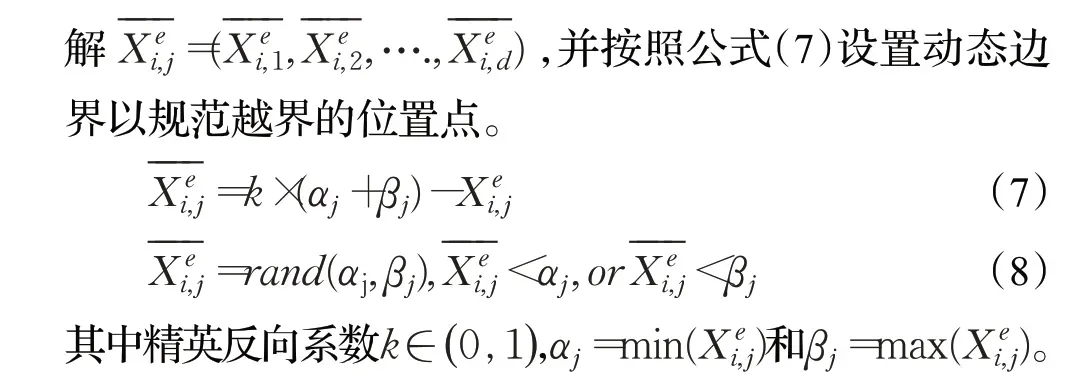
最后，将混沌生成的所有初始解和混沌精英反向解合并进行排序，选取前N个较优的解作为初始种群。

2.2 单纯形法

单纯形法是一种不受目标函数连续性和可导性影响的直接搜索算法，其主要通过迭代判断最差顶点Xs向优运动的方向向量g是否正确，并通过对最差顶点进行反射、扩张、外收缩和内收缩操作来控制其运动。单纯形法步骤如图2所示。

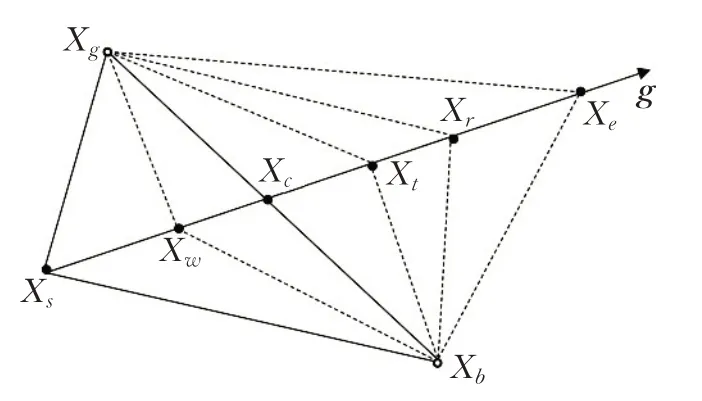
图2 单纯形法示意图Fig.2 Diagram of simplex method

具体流程如下：

（1）计算种群的适应度值，并将最优的4 个位置分别记为XAttacker、XBarrier、XChaser和XDriver，对应的适应度值为f(XAttacker)、f(XBarrier)、f(XChaser)和f(XDriver)，设中心位置为Xc=(XAttacker+XBarrier)/2。

（2）将剩下黑猩猩个体的适应度值进行排序，选择适应度值最差的个体作为较差点Xs。

通过运用单纯形法的4种操作，可以让最差点在反射操作下搜索到所有可行的解，内外收缩操作可以使最差点摆脱当前位置，而在扩张操作下可以让最优解跳出局部最小值，向距离最差点更远的反方向继续搜索，从而提高了算法整体的局部开发能力和寻优能力。由于单纯形法针对的是种群中最差的个体，对于种群中其他个体仍然执行黑猩猩原始算法中的随机搜索，故而在提高算法的局部搜索能力的同时，不会降低种群的多样性。

2.3 群个体记忆机制

在原始COA算法中，通过对群体历史前4个最优位置的加权记忆，实现了黑猩猩种群间信息交流，最终促使个体在搜索空间快速移动寻优，但这一做法并未考虑到每个黑猩猩个体自身的搜索经验，因而，在结合COA算法群体信息交流表达式（5）的基础上，引入粒子群算法的个体记忆策略，具体表达式变为：

其中，b1和b2是[0，1]间的常数，分别表示群体交流和个体经验记忆的系数；rand表示[0，1]间的随机变量；Xbest表示第i只黑猩猩所经历过的最佳位置，Xj,Xi,(j≠i)是记忆过程中记下的随机个体位置。通过对b1和b2的调节来平衡群体交流和个体记忆对位置更新的影响。

对比原始位置更新方程式（5），式（9）增加了两个部分：第一个是引入的个体自身记忆信息，进一步提高了算法在局部的开发能力和收敛速度；第二个是随机记忆的个体位置，从而起到增强算法种群多样性和全局勘探的能力。

2.4 算法步骤

综上所述，本文提出EOSMICOA 算法的运算步骤如下：

步骤1 设置相关参数，种群规模N、最大迭代次数tmax、收敛因子f、影响系数A、C、混沌因子m等。

步骤2 利用Iteration 混沌映射和精英反向学习生成初始种群Xi,i=1,2,…,N。

步骤3 计算个体的适应度值，并确定历史前4个最优解XAttacker、XBarrier、XChaser和XDriver。

步骤4 利用单纯形法改变较差个体Xs的位置。

步骤5 更新A、C，按照公式（5）计算其他黑猩猩的位置。

步骤6 通过粒子群算法改进的群个体记忆机制，按照公式（9）进一步更新黑猩猩位置。

步骤7 判断算法是否达到最大迭代次数，若达到，则算法结束，输出最优位置XAttacker；否则，执行步骤3。

3 实验仿真与结果分析

3.1 实验参数设置

本文选取了COA、WOA、EOSMICOA 和当前最新改进算法EGolden-SWOA、IGWO，在20 个测试函数上进行实验对比。

以上算法统一参数设置如下：种群规模N为30，最大迭代次数tmax为500，运行次数为30，低维实验维数为30，高维实验维数为1 000。

3.2 测试函数

为检验EOSMICOA 的优化性能，选取表1 的20 个基准测试函数进行仿真实验分析，并给出表达式、搜索范围和最优值，其中f1～f7为7个连续单模态测试函数，用来测试算法的寻优精度，f8～f13为6个连续多模态测试函数，f14～f20为7个固定多模态测试函数，用来测试算法的全局搜索能力和收敛速度。

表1 基准测试函数Table 1 Benchmark functions

3.3 多种启发式算法比较

3.3.1 算法实验结果对比

表2、3和表4列出COA、WOA、EOSMICOA、EGolden-SWOA、IGWO 在d=30 和d=1 000 的低维、高维状态下的7 个单模态和6 个多模态测试函数，以及在7 个固定模态测试函数上分别独立运行30 次实验后，得出的最优值、平均值和标准差。其中每个测试函数的最优结果均加粗处理，最优值可以显示出算法的寻优能力，平均值可以用来反映算法总体所能达到的收敛精度，标准差则反映出算法的鲁棒性和稳定性。

从表2的低维单模态测试函数的比较结果可知，总体看，无论是在低维30维还是高维1 000维上EOSMICOA在f1～f7这7 个测试函数上均显现出最好的寻优能力。对于f1、f3，EOSMICOA的寻优性能最好，甚至可以直接寻到最优值0，在f2、f4上，EOSMICOA 的平均寻优精度均在10-200以上，且EOSMICOA在这4个函数上的标准差均为0，说明EOSMICOA 不论高维还是低维，算法的稳定性和鲁棒性都同样良好；其次，是改进算法EGolden-SWOA的寻优能力，在f1～f7函数上也表现出优良的寻优效果，甚至在低维情况下的f1和f3，可以直接收敛到最优值，在低维的f4、f5、f7的平均寻优精度仅次于EOSMICOA，甚至在低维的f5、f7上可以达到几个算法最高的精度，但标准差却高于EOSMICOA，但是，在高维实验中的表现依然劣于EOSMICOA；其次表现较好的是标准COA 算法，其寻优效果和算法的稳定性在f1～f7函数上均比改进算法IGWO 要好，可见标准COA 算法在算法的设计上具有一定优越性，而对COA的改进研究也更具有重大意义。最后表现较好的是IGWO，除了低维的f1、f2实验上的寻优精度比不过WOA，但在高维实验中，IGWO 的表现比较稳定，在剩下的f3、f4、f5、f6、f7中的高、低维实验中均比WOA的寻优效果理想，而WOA的表现相对较差。

表2 单模态测试函数实验结果Table 2 Experimental results of single mode test functions

从表3的多模态测试函数的实验结果比较可知，在f8～f13函数的高维和低维实验中上，EOSMICOA 依然表现出不同寻常的寻优能力。尤其是在f9～f11函数上，EOSMICOA 的寻优精度极佳，可以直接寻到最优值0，在f10、f12、f13的高、低维实验上，EOSMICOA最优值、平均值和标准差均是4个算法最小的，说明EOSMICOA在多模态测试函数高、低维实验上上仍然具有相对最优良的寻优能力和算法稳定性；其次，表现优良的是改进算法EGolden-SWOA，在f8上的最优值是几个算法中的最优结果，但其标准差也最大，在f9、f10、f11这3个函数上可以和EOSMICOA 一样达到最优结果；接着，表现最好的是IGWO，在f9、f10、f11函数上，IGWO 在高维实验的寻优能力和稳定性甚至比在低维实验上的要好，可以从中发现IGWO 比起低维函数，更适合用于高维函数问题，在剩下的4个函数中的寻优表现均要胜于标准的COA和WOA算法；最后，WOA在f8～f13的低维和高维实验中，寻优精度和稳定性均比COA要好，甚至在f9、f11两个函数的高、低维实验上的最优值均可以和EOSMICOA 一样直接收敛到0，而相对其他几个算法在多模态测试函数上实验结果而言，COA 的表现最差。

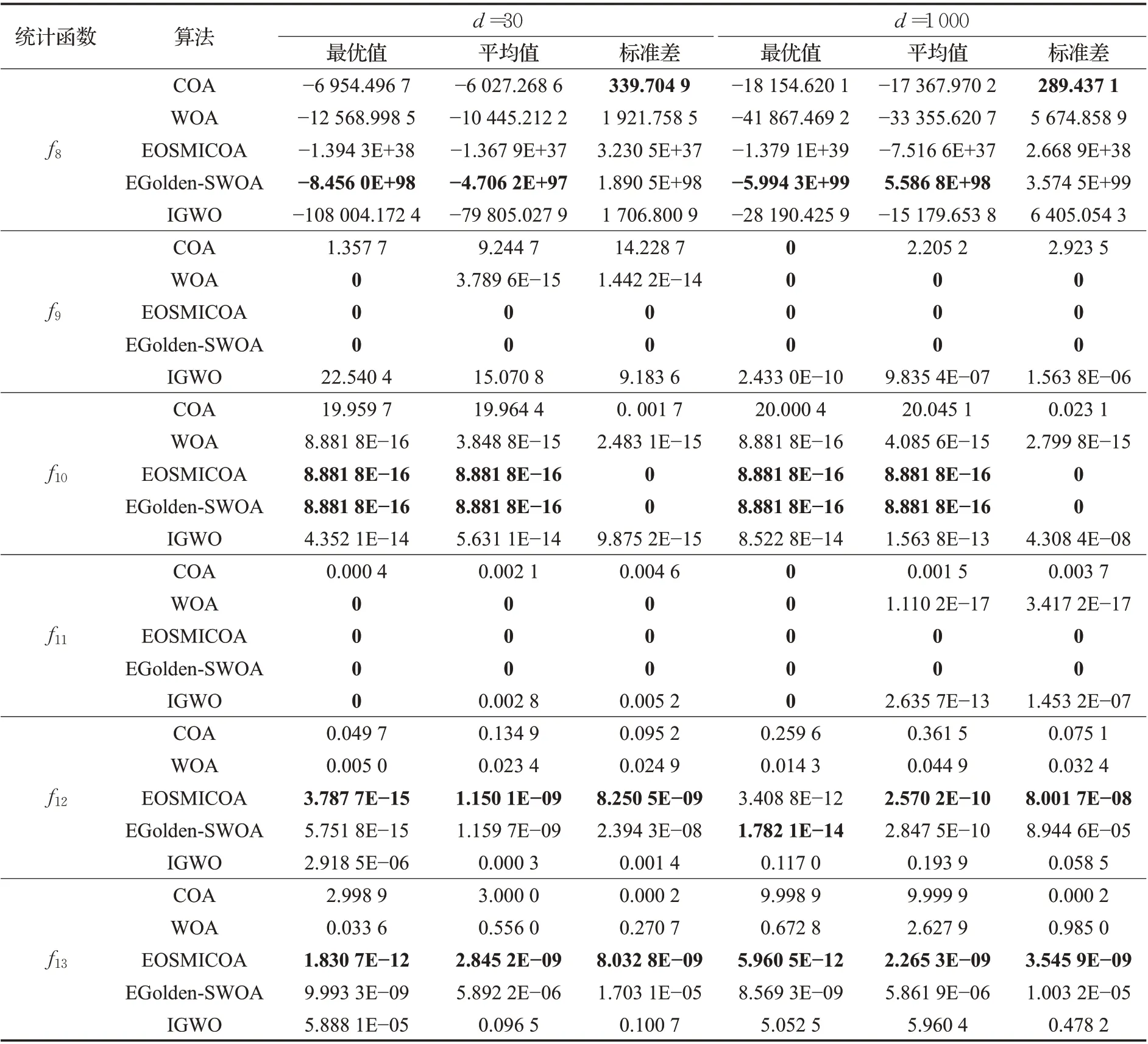
表3 多模态测试函数实验结果Table 3 Experimental results of multimodal test functions

在表4固定多模态测试函数的实验结果对比中，可以发现EOSMICOA在7个固定模态的测试函数上的寻优精度都达到了最高，在前面13 个复杂函数的高维实验中表现不好的IGWO 在这7 个固定模态的测试函数上的表现也发生变化，拥有较高的算法稳定性，而EGolden-SWOA的表现则位列第三。

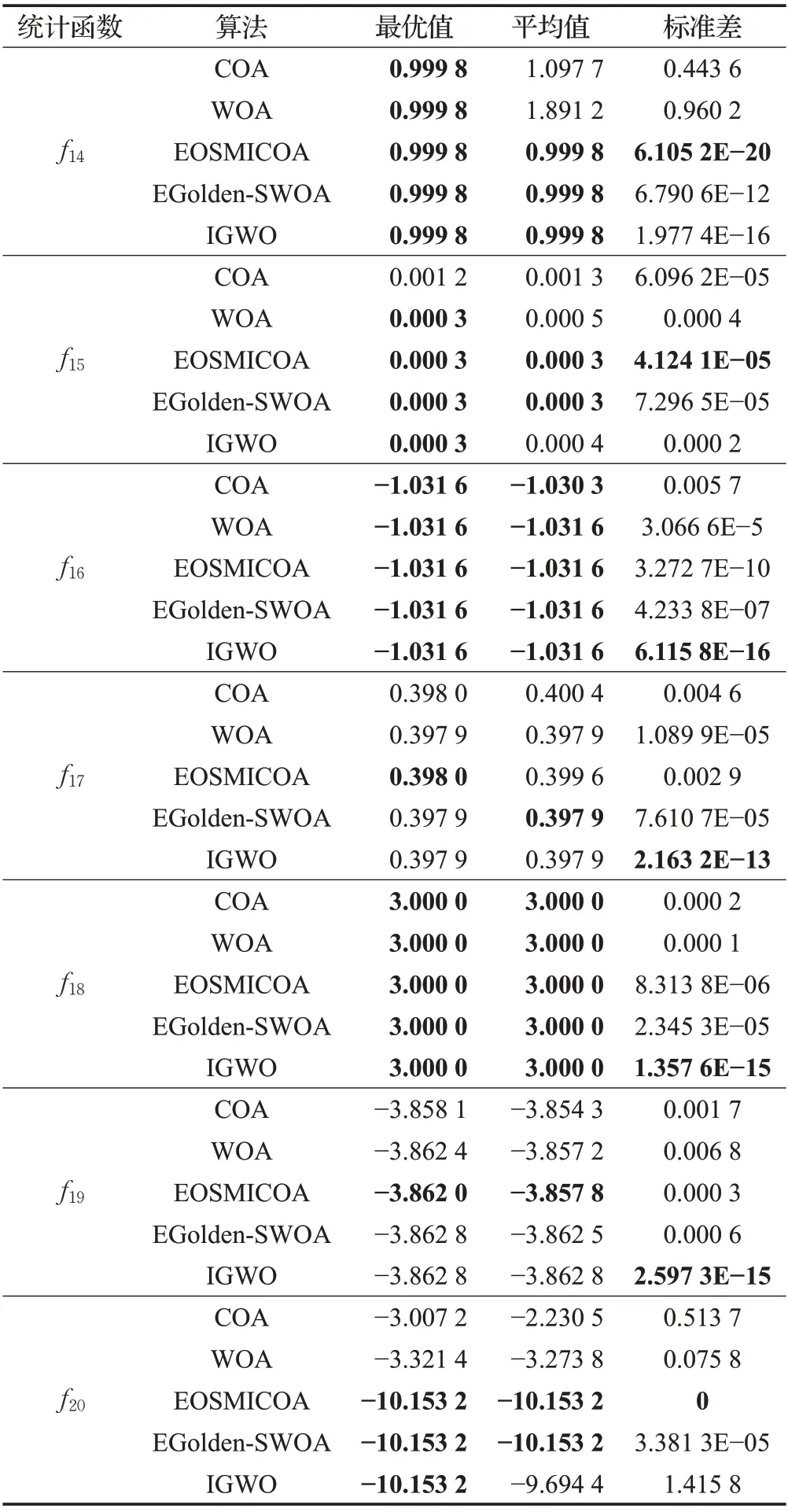
表4 固定多模态测试函数实验结果Table 4 Experimental results of fixed multimode test functions

EOSMICOA、EGolden-SWOA、IGWO 这3 个算法在f15、f16、f18和f20中都直接收敛到最优值0.000 3、-1.031 6、3.000 0和-10.153 2，但相比之下IGWOA的标准差在f16、f18上最小，而EOSMICOA在f15、f20的标准差最小，说明IGWO 和EOSMICOA 的稳定性和鲁棒性都较好；在f14、f17、f19中，EOSMICOA 均获得了几个函数中的最佳精确度，在f14上的标准差也最小；显然，表现较好的IGWO和EGolden-SWOA在算法的稳定性和寻优能力上各有千秋，IGWO拥有较高的算法稳定性，而EGolden-SWOA的收敛精度要高于IGWO；最后，标准COA 和WOA 在固定模态测试函数的实验中表现最弱。

通过EOSMICOA、EGolden-SWOA和IGWO这3个改进算法在13 个单模态、多模态复杂函数的高维实验和7个固定模态函数的实验对比中，可以发现EOSMICOA的寻优精度最佳，且迭代和运行过程中表现出优秀的稳定性和鲁棒性。尽管在部分函数上，EGolden-SWOA和IGWO 也可以收敛到函数最优值，但根据图3 的5个函数收敛图可以发现，EOSMICOA 寻到最优值所需要的迭代次数均小于EGolden-SWOA，在f1和f3上，EOSMICOA 寻优需要迭代的次数甚至比EGolden-SWOA少100次，比IGWO则少300次；在f9、f10、f11上，EOSMICOA寻优需要迭代的次数比EGolden-SWOA 少至少50次，比IGWO则少200次。

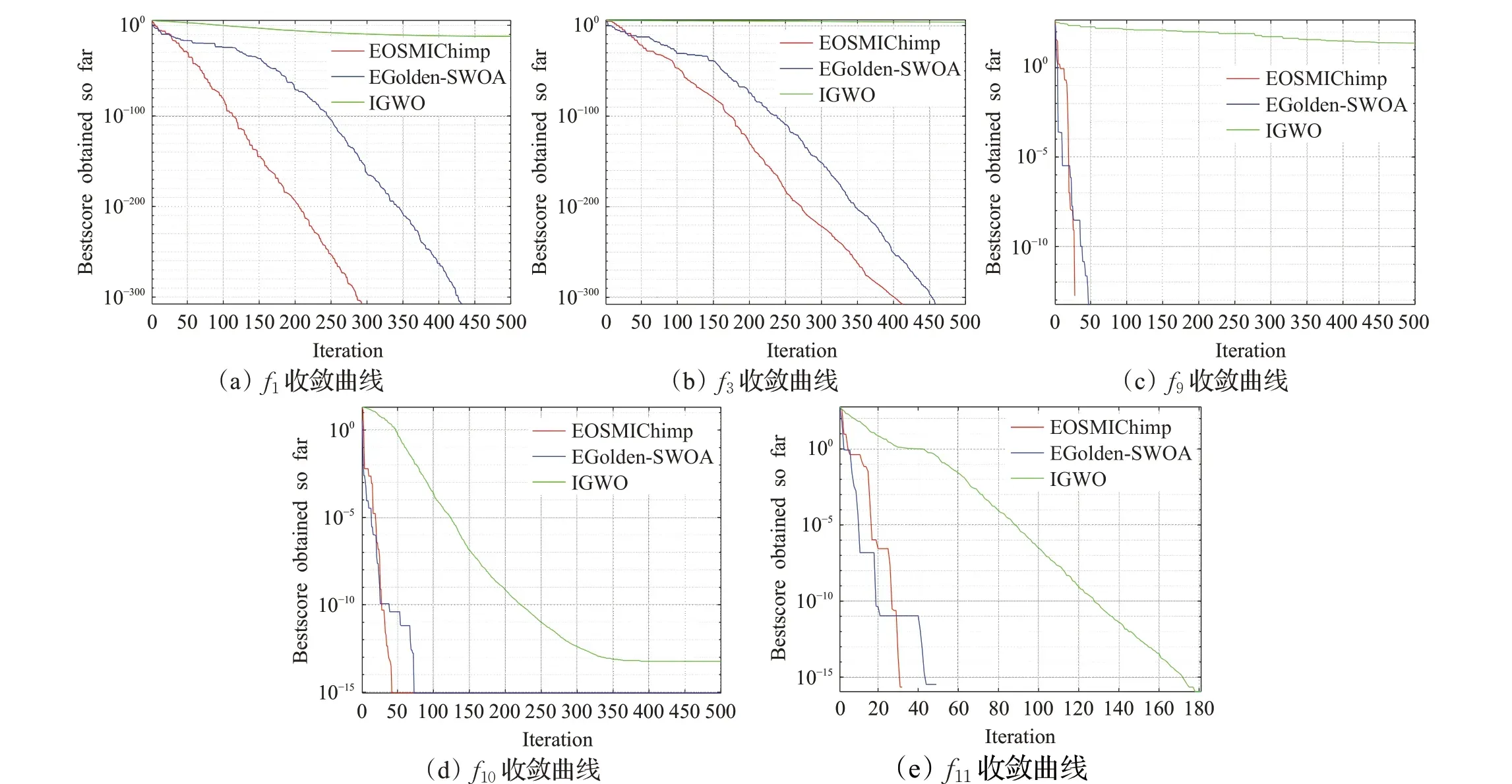
图3 函数收敛图Fig.3 Function convergence diagram

综上表明，EOSMICOA 除了取得较高的收敛精度以外，更在收敛速度上有较大的提高，这归功于改进策略中的单纯形法和群个体记忆机制。单纯形法通过运用4 种操作改变最差个体的位置并不断更新最差个体的方法来提高算法跳出局部最优解的能力，但并不能大幅提高算法整体的收敛速度，由此，加入的群个体记忆机制可以将最优位置信息成功地传递给下一代个体并记录下来，从而减少搜寻较差解的时间，大大加快了算法的寻优速度，同时记忆过程中记下的随机个体位置也可以使算法在后期保持良好的种群多样性，起到了平衡算法在局部开发和全局勘探能力的重要作用。

3.3.2 时间复杂度分析

EOSMICOA 主要由Iteration 映射和精英反向学习结合的混沌反向学习策略初始化种群、单纯形法和群个体记忆机制等操作组成。当算法的种群规模维N，问题维度维d，最大迭代次数为tmax，每个操作的时间复杂度如下：混沌反向学习策略初始化种群的复杂度为O( (N+N×d)×tmax)，单纯形法的复杂度为O(N×tmax)，而群个体记忆机制的复杂度为O(N×d×d×tmax)，EOSMICOA 整体复杂度为O(tmax×N×d×d)，而COA和WOA 的复杂度为O(tmax×N×d)，EGolden-SWOA的复杂度为O(tmax×N×d×d)，IGWO 的复杂度同样为O(tmax×N×d)。因此相比几个算法，EOSMICOA和EGolden-SWOA 的时间复杂度相同，而比标准COA、WOA和IGWO高，但也在可以接受的范围内。

4 EOSMICOA算法的焊接梁设计应用研究

为验证EOSMICOA 在解决实际问题中的有效性，将其应用于机械设计中的复杂优化问题，即焊接梁最小费用问题，其设计原理示意图如图4所示。

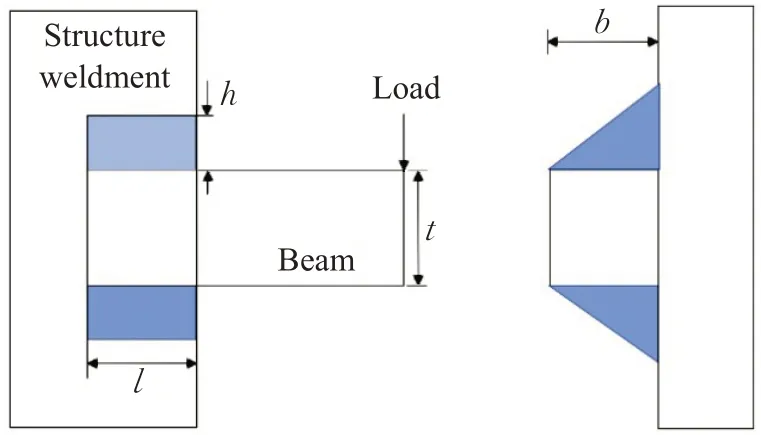
图4 焊接梁设计原理Fig.4 Design principle of welded beam

焊接梁设计问题的目标是使其制作成本最小，图4为焊接梁设计图，其约束变量为剪切应力τ，梁弯曲应力σ，杆曲载荷Pc和梁端挠度δ，此设计问题所需要优化的变量为焊缝厚度h、夹条长度l、梁长t和梁宽b，这4个优化变量的目标函数和约束条件如下：

分别利用EOSMICOA 算法、EGolden-SWOA 算法和CPSOGSA算法进行求解，参数设置相同，3种算法分别运行30次求解结果的最优值、平均值和标准差如表5所示，图5 为3 种改进算法求解焊接梁设计问题的收敛曲线。

从表5 的对比结果，可以清楚地发现，在求解焊接梁工程设计这一复杂优化问题时，EOSMICOA 的表现最佳，其设计出的焊接梁成本最优情况下可以达到1.695 6，远低于EGolden-SWOA 和CPSOGSA 的最优值，且总体平均也要优于其他两个改进算法；虽然从求解结果的稳定性来看，EOSMICOA 的标准差要高于EGolden-SWOA，但相差并不太大，且仍然比CPSOGSA的标准差要低。从图5的3种算法的求解结果收敛曲线也可以发现，EOSMICOA的收敛速度是3种改进算法中最快的，在200次迭代后就基本寻到最优值，而EGolden-SWOA和CPSOGSA在500次的迭代内无法收敛到比较好的结果。

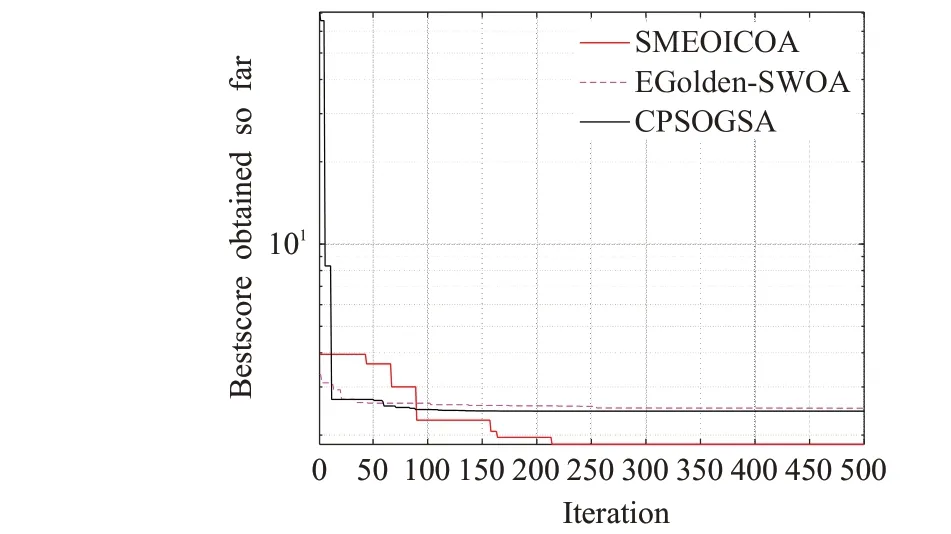
图5 焊接梁设计问题求解结果收敛曲线Fig.5 Convergence curve of solution result of welding beam design problem

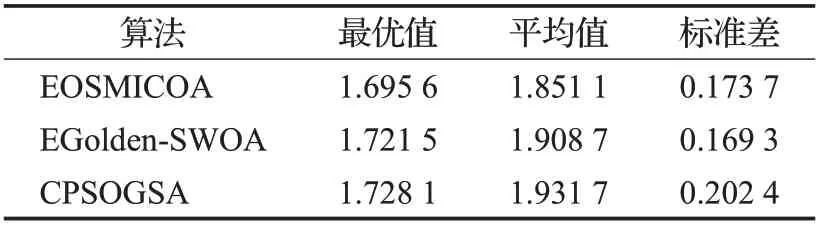
表5 焊接梁设计问题3种算法求解结果对比Table 5 Comparison of three algorithms for welding beam design

5 结束语

本文针对原始黑猩猩优化算法存在的依赖初始种群、收敛精度不高、容易陷入局部最优等问题，提出来一种多策略黑猩猩优化算法：EOSMICOA。利用无限折叠迭代混沌映射（Iteration映射）和精英反向学习策略的结合初始化种群，并应用单纯形法和群个体记忆机制改进个体的位置，使得原始算法在提高寻优精度的同时大大提高收敛速度，也为进一步改进启发式优化算法提供新的改进优化策略方案。EOSMICOA这一改进策略的效果，通过在13 个复杂测试函数的低维和高维实验以及7 个固定多模态复杂函数上与多种算法的比较中得以展现，但EOSMICOA在面对函数f5～f7、f12时，仍有进一步提升收敛精度的空间。同时，将EOSMICOA 应用于焊接梁设计这一复杂工程优化问题中也得到比较好的结果，说明改进的EOSMICOA 在实际工程问题中也具有良好的适用性。下一步的研究内容将考虑继续提升EOSMICOA 算法在全局寻优的能力，并将其与深度学习结合起来应用于现实问题中。