假定旋转坐标系下的永磁同步电机无位置传感器算法研究

储剑波， 陶楷文， 朱叶

(1.南京航空航天大学 自动化学院， 江苏 南京 211106； 2.航空工业金城南京机电液压工程研究中心，江苏 南京 211106)

0 引 言

在多电飞机电动环境控制系统中，高速永磁同步电机(high speed permanent magnet synchronous motor,HSPMSM)是驱动压气机进行环控的核心部件[1]，出于可靠性考虑，控制系统往往会配备一套无位置传感器算法以应对位置传感器故障情况。由于电动环控HSPMSM系统具有宽调速范围、重载、大惯量特点，因此无位置传感器算法参数的调节十分关键，不理想的参数极易导致系统发生振荡,无位置传感器算法的参数设计研究至关重要。

高速无传感器算法一般通过计算永磁同步电机中含有位置信息的磁通或反电势电气量间接实现角度与转速观测，常用的观测器包括扩展卡尔曼滤波法[2]、滑模观测器[3-4]、模型参考自适应观测器等。具有参数自适应的扩展卡尔曼滤波法近年来被广泛研究[5-6]，在迭代运算中计算测量值与预测值波动情况，实时修正误差协方差矩阵。该类算法复杂度高，且参数初值设置仍然具有难度，难以在高控制频率，大功率工况下应用。滑模观测器法具备参数整定方案基础，高频开关函数设计简单、容易实现。然而，高速工况下滑模观测器的抖振现象使得系统控制稳定性变差，一般需要在观测器中加入滤波器去除噪声，减少抖振。文献[7]将Sigmoid函数引进滑模观测器来抑制抖振，省去了滤波环节和相位补偿环节，与传统滑模观测器相比抖振有所减少，但是牺牲了算法的滑动特性。此外，近年来还有学者提出超扭滑模算法[8-9]，高频开关变量保证了观测所得扩展反电势(extended back EMF,EEMF)能够收敛至实际EEMF，且新的积分部分降低了抖振现象，该类算法主要缺点在于待设计参数多，系统建模困难，复杂度较高，且带有滤波特性的开关函数会导致观测信号相位延迟，造成位置信息观测误差。

文献[10]提出了一种假定旋转坐标系下的无位置传感器算法，并在额定功率与转速分别为75 kW、27 000 r/min的高速永磁同步电机上进行了实验验证。该方法通过构造假定旋转坐标系，建立与实际d-q轴电压方程关系获取角度误差量，再通过锁相环进行位置信息重构，提取角度与转速信息。该方法结构简单，位置信息误差量直接输入至锁相环，无需进行任何滤波处理，不会带来抖振与观测量相移问题。针对该方法，本文提出一种基于观测器传递函数分析与基于系统小信号模型的稳定性分析[11]相结合的参数设计方案，并利用模糊控制器对算法进行改进，得到具有参数自适应功能的假定坐标系下的无传感器控制方法。所提改进方法复杂度低，整定方案简单，且动稳态性能得到提升。在实际电动环控用HSPMSM系统中得到了验证。

1 基于假定坐标的控制方法

d-q轴旋转坐标系中永磁同步电机(permanent magnet synchronous motor, PMSM)的电压方程为

(1)

式中：vd、vq分别为d、q轴电压；id、iq分别为d、q轴电流；Ld、Lq分别为d、q轴电感；Rs为定子电阻；ψf为永磁体磁链；ωe为转子电角速度。

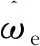
图1 永磁同步电机模型

将式(1)[12]重写为

(2)

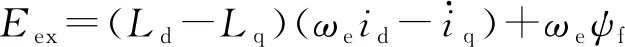
经过上述数学处理后，将电压方程变换到γ-δ估计旋转轴坐标系下，得到

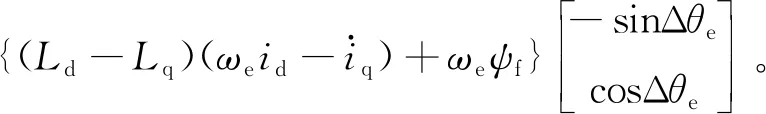
(3)

(4)

(5)

位置观测器正常运行过程中，Δθe项为无穷小量，因此式(4)存在以下近似关系：

(6)

并且忽略反电势中的微分项，γ轴反电势可以进而表示为

eγ=vγ-Rsiγ+ωeLiδ。

(7)

γ轴反电势含有角度误差信息，利用角度误差通过锁相环进行位置信息重构。最终位置观测器方案框图如图2所示。

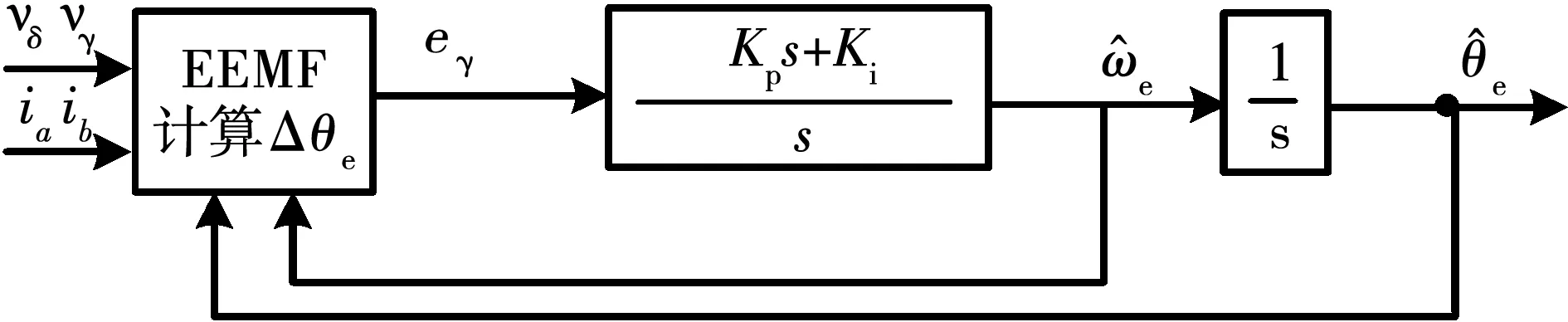
图2 假定坐标下的位置观测器

2 位置观测器参数整定

2.1 传递函数参数分析

由图2可得，位置观测器的开环传递函数为

(8)

由开环传递函数可知位置观测器为典型的Ⅱ型系统[13]。将传递函数写为关于阻尼比ξ与自然频率ωn参数的关系式，替代PI环参数，写出闭环传递函数为

(9)

式中阻尼比与自然频率和位置观测器比例积分参数存在以下关系：

(10)

确定阻尼比ξ：在位置观测过程中，更希望观测稳定，不产生超调与振荡且允许存在一定角度滞后，根据极点分布特性可知，选取临界阻尼或过阻尼状态时，系统时间响应无振荡，单调上升，此时阻尼比选取ξ=1或ξ>1。

给定输入为单位斜坡，自然频率ωn为1 rad/s，由图3(a)可得，选取0<ξ<1时，系统内存在振荡情况，收敛较慢。ξ=1时，系统无振荡，单调上升且收敛快速，对比选取ξ=1更为合适。由图3(b)可得，当ξ>1时，调节时间更快且同样无振荡，而相比于ξ=1收敛较慢，综合考虑针对位置观测器阻尼比ξ选取为1时更优。

图3 不同阻尼时的斜坡响应

确定自然频率ωn：针对不同转速运行状态，由式(10)闭环传递函数，可得该二阶系统斜坡与加速度时间响应函数。在ξ=1下单位斜坡响应时间函数与单位加速度响应时间函数分别如式(11)与式(12)所示。

单位斜坡响应为

R(t)=-t·(e-ωn·t-1)。

(11)

单位加速度响应为

(12)

给定斜坡与加速度时间响应函数衰减项都与自然频率正相关，自然频率ωn越大，衰减越快，则观测器响应越快。此外，当系统输入为加速度函数时，系统存在直流偏置，且该直流偏置的大小与自然频率直接相关。同时，对于Ⅱ型系统，加速度响应存在稳态误差，当输入加速度函数C(t)=R·t2时，稳态误差为

(13)

综上可得，自然频率ωn越大，观测器响应越快，且稳态误差越小，针对该观测器而言，在确定的阻尼比ξ=1下，选取更大的ωn系统性能更优。然而观测器局部结论并不完全适用于系统，ωn的增大会对系统造成负面影响，下文对基于该算法的HSPMSM系统进行小信号模型稳定性分析。

2.2 位置观测器下系统稳定性分析

在位置观测器局部分析基础上，进一步确定参数范围。电机系统为非线性系统，稳定性分析需将非线性系统进行局部线性化。通过选取稳态工作点，施加小扰动信号，建立用于稳定性分析的线性模型。

2.2.1 非线性模型

PMSM模型状态方程为：

(14)

式中：p为微分算子；J为转动惯量；P为电机极对数；TL为负载转矩。

转速环PI控制器状态方程：

(15)

式中Kps，Kis分别为转速环比例与积分系数。

d轴电流环PI控制器的状态方程：

(16)

式中Kpd、Kid分别为为转速环比例与积分系数。

q轴电流环PI控制器的状态方程：

(17)

式中Kpq、Kiq分别为转速环比例与积分系数。

位置观测器中转速估算状态方程：

(18)

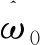
引入一阶低通滤波器减少估算转速高频噪声。速度估算经过低通滤波器输出，为

(19)

估计角度的误差表达式为

(20)

电机运行在稳态时，各个变量微分值为0，于是可以求解各参数稳态值。

2.2.2 线性模型

通过在稳态情况下对系统施加小扰动，系统中的各变量将在稳态值附近产生一定的增量，将状态方程中的状态量都表示为线性增量，即可得到用于小信号分析的线性模型。将式(14)进行小信号模型处理，其表达形式为：

(21)

式中As和Bs以及BT如下，其中：

as1=

在小扰动信号下，角度估测误差被认为是无穷小量，于是两坐标轴电压电流关系为

(22)

将式(22)代入式(15)～式(20)，整理成矩阵形式，得到状态变量方程为：

(23)

式中Aw和Ax以及Br如下：

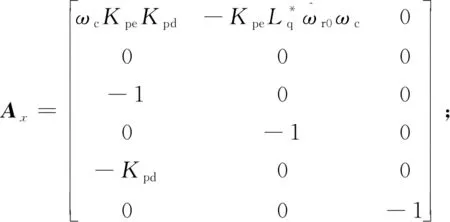
同时将PMSM中的输入量Δus也表示为状态变量形式：

Δus=FwΔw+FxΔxs+FrΔr。

(24)

其中：

整合式(21)、式(23)、式(24)可得系统线性状态方程为

(25)

2.2.3 稳定性分析

以位置观测器自然频率参数作为变量，绘制其特征根轨迹，分析系统性能。选取阻尼比ξ=1，此时位置观测器PI参数为：

(26)

采用id=0的矢量控制方法，电流环闭环带宽设置为1 000 Hz，转速环闭环带宽设置为10 Hz，转速环滤波设置为300 Hz。选取稳态工作点，当电机运行在旋转角速度为45 000 r/min，负载转矩为6 N·m的情况下，根据电机方程，计算出各理论值。认为在稳定工作时，d-q轴电流与估计旋转轴γ-δ轴电流一致，估算角度误差Δθe作为无穷小量。将位置观测器中的自然频率ωn从0 rad/s逐渐增大至455 rad/s，绘制HSPMSM系统的特征根轨迹图。

由式(25)可知，对于每个给定自然频率ωn有8个特征根解，其中6个均为负实数根，只有1对共轭特征根。再结合所绘制的特征根轨迹图，4个负实数根不随自然频率变化而变化，另外2个负实数特征根随自然频率增大远离虚轴，不影响系统稳定性。只有唯一一对共轭特征根影响整个系统稳定性，图4绘制了共轭特征根轨迹中的其中一条，作为主导特征值进行分析。由主导特征值变化趋势可知，系统输出转速响应随着自然频率ωn的上升，先是远离虚轴，随后出现拐点开始靠近虚轴，拐点即为图4中标记的ωn=115 rad/s处。继续升高自然频率ωn，系统特征根向虚轴逼近得越来越快，当ωn>450 rad/s时特征根移动至右半平面。

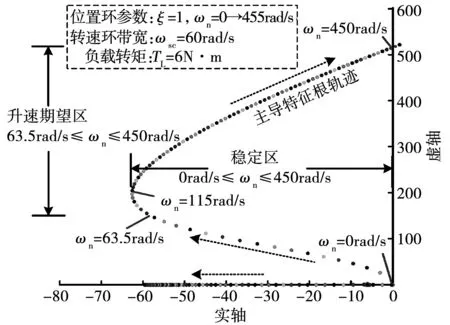
图4 基于变自然频率参数的特征根轨迹图

综上可得，当0≤ωn≤450 rad/s时系统极点分布均在左半平面，根据李雅普诺夫稳定性判据可知系统稳定。

2.3 参数稳定范围确定

通过观测器局部分析，在斜坡转速给定的情况下，存在角度固定误差，且该稳态误差与转速给定斜率R及自然频率ωn相关。转速上升斜率由工程需求所决定，通过设定最大角度误差eexp，确定自然频率范围，为

(27)

系统输入给定转速上升斜率为10 000(r/min)/s，要求角度误差范围控制在电角度15°以内，由式(27)求得自然频率带宽范围ωn≥63.55 rad/s，再由系统根轨迹图可知，稳态状况下自然频率最大为450 rad/s系统能够保持稳定，为保证动态角度误差在期望值以内且系统稳定要保证63.55≤ωn≤450 rad/s，该范围即为位置观测器参数最终选取范围。

3 基于模糊PI的锁相环设计

确定参数选取范围后，最优参数难以选取。局部传函分析可知，升速过程存在稳态角度误差，而大功率下系统角度误差导致功角减小，电流升高，效率下降明显，针对动态升速更希望取较大自然频率保证观测精度。系统稳定性分析可知，自然频率进一步升高向虚轴靠近，李雅普诺夫第二定理可知系统高频噪声增加，导致稳定性变差。基于分析所得参数特性与选取范围，利用模糊PI控制器替代锁相环中传统PI控制器，针对系统不同运行状况调节位置观测器自然频率，达到算法参数自适应目的。应用于无位置传感器中的模糊PI控制器如图5所示。

图5 模糊PI控制器框图

1)输入输出量选取。

位置观测器中的模糊PI控制器采取的是双输入单输出结构，原理更为简单。其输入为角度误差的与角度误差的导数，输出为位置观测器的自然频率ωn。角度误差Δθe的物理论域为[-π/24，π/24]，角度误差变化率等效为转速误差波形，认为在电机运行过程中位置观测器估计转速能够稳定跟踪实际转速，则该输入量物理论域就是观测器高频噪声带来的，设置为[-3 000，3 000]。输出物理论域选取为特征根轨迹升速期望点至稳定范围上限值即[63,450]。

2)量化因子与比例因子的确定。

模糊论域的选取决定了量化因子与比例因子。模糊论域的选取直接决定了控制器设计的复杂程度，更大范围的模糊论域意味着更高的控制精度，相应也带来了较大的设计难度，反之小范围模糊论域设计则会使得控制器精度变差与系统响应速度增快。考虑到HSPMSM系统高频特性，在保证一定的控制精度情况下，算法越精简越有利于减小控制系统执行压力，因此尽可能降低模糊控制器的复杂度是设计目标之一，因此，权衡快速性与精度考虑，选取模糊论域为[-3,3]。则量化因子分别为72/π和1/500，比例因子为387/6。

3)隶属函数的选取与控制规则设计。

隶属函数常用的有高斯型、三角形、梯形三种，其中三角隶属函数曲线坡度最陡，具有更高的分辨率，控制灵敏度也更好，适用于既要保证快速性又要尽量减小算法复杂度的HSPMSM系统，因此选用三角函数作为控制器隶属函数。图6给出了典型的不同自然频率下位置观测器角度误差波形图，依据此图设计模糊规则。

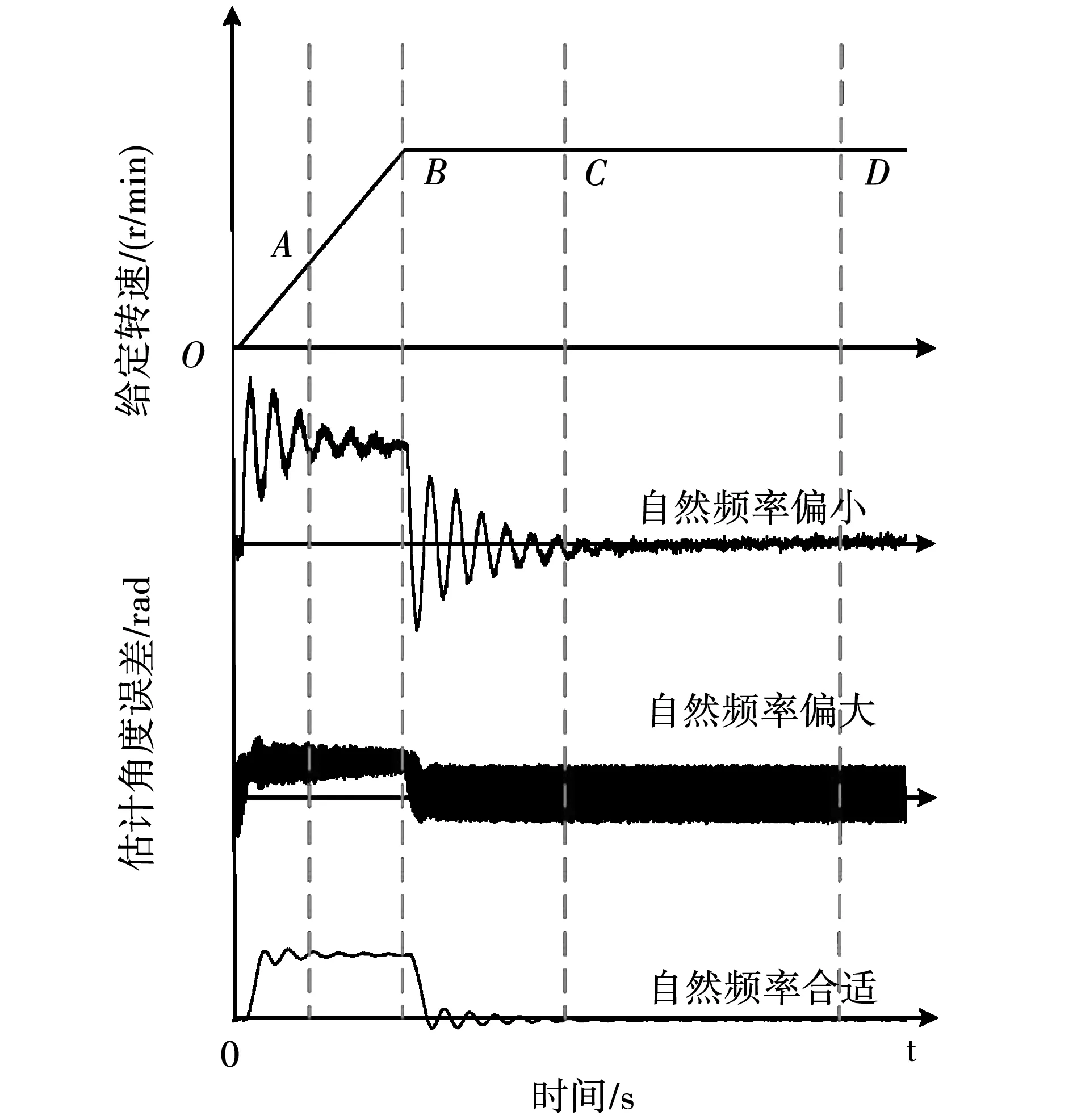
图6 典型不同自然频率下角度误差响应

OA段：电机升速，角度估计误差迅速增大，与此同时角度估计误差导数也达到最大，此时若自然频率偏小，角度误差响应出现较大波动，且收敛缓慢，需要快速增大自然频率ωn提高响应速度降低角度误差。

AB段：升速过程中已经达到稳定跟踪，角度误差不再波动，此时适当减小自然频率的增长。

BC段：系统达到给定转速，位置观测器再次处于振荡状态，在经历OA段自然频率的调整过后，若振荡依旧偏大则继续扩大自然频率值该阶段结束，即系统收敛。若OA段自然频率被调节至偏大状态，系统会迅速收敛至给定转速，且此时角度误差高频振荡，导致转速波动加剧，也就是角度误差导数变大，此时应该缓慢减小自然频率，保证转速收敛的情况下稳态性能自适应至最优。

CD段：转速已达到给定转速且振荡结束，此时角度误差接近为零，若自然频率偏大则角度误差导数偏大，须进一步降低自然频率，当模糊控制器输入均控制在零附近时不再调节观测器参数。

模糊规则表如表1所示，图7为模糊规则对应可视图。

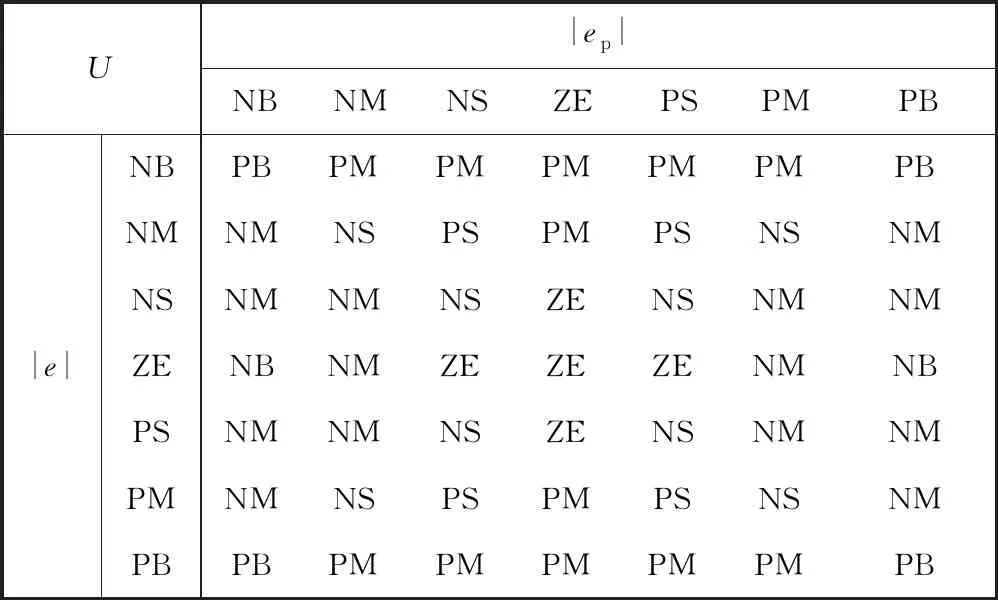
表1 ωn的模糊控制规则表

图7 模糊规则可视图

4 仿真验证

在MATLAB/Simulink中对该方法进行了模型搭建和仿真研究，仿真中的电机参数和各调节器参数与稳定性分析中的各参数一致。

转速上升斜率为10 000 (r/min)/s，目标转速45 000 r/min，给定不同自然频率ωn观测角度误差波形，如图8所示。

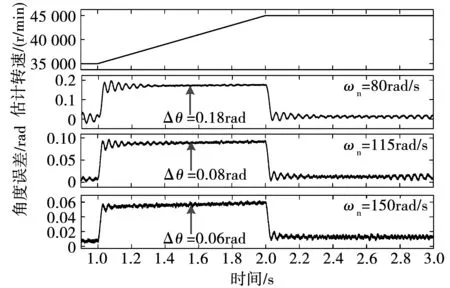
图8 角度误差与自然频率关系图

图8中分别选取了三个不同的自然频率值ωn=80、ωn=115，ωn=150 rad/s，利用式(13)计算得出理论稳态角度误差值分别为0.164、0.08、0.06 rad，仿真结果与理论对应。

给定ωn=450 rad/s，仿真情况如图9所示。转速能够收敛至给定值，然而转速误差与角度误差出现高频振动，稳定性差。当选ωn=480 rad/s时，系统出现发散情况。此外，选取自然频率450 rad/s应用于实际系统中时，系统由于高频振动直接出现了发散情况，该参数仅能用在仿真中且此时转速波动较大。

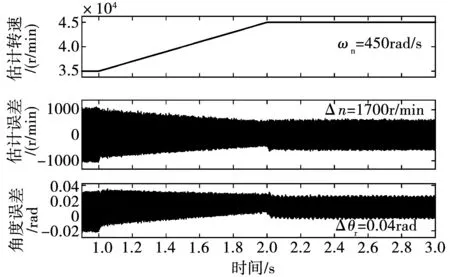
图9 临界稳定ωn=450 rad/s下输出波形图

选取ωn=80、115、215、315 rad/s，转速给定45 000 r/min时，不同自然频率对转速波动情况与角度波动情况的影响。由图10和图11可知，自然频率的升高，转速波动加剧，角度都在0 rad上下波动观测结果准确。自然频率选为315 rad/s时，转速波动达到了160 r/min，继续增高自然频率转速波动更为剧烈。

图10 自然频率与转速误差关系图

图11 自然频率与角度误差关系图

将模糊PI应用于无位置传感器算法观测器，与传统PI进行仿真对比研究。由图12(a)可知，传统PI下，ωn=115 rad/s时稳态时转速波动在20 r/min内，升速过程中波速误差在200 r/min左右，输出转速动稳态运行性能良好。而ωn=450 rad/s时稳态转速波动达到1 800 r/min，波动剧烈，动态升速误差也达到了800 r/min，全速段运行效果差。基于模糊PI的无传感器算法在升速过程中转速波动在200 r/min以内，稳态运行过程中转速波动仅有20 r/min，无论在动态升速还是稳态运行过程中都有良好的运行效果。

由图12(b)可得，选取ωn=450 rad/s时动态升速与稳态运行过程中角度误差都在0.01 rad以内，角度观测准确，然而高频噪声剧烈。ωn=115 rad/s时，动态升过程中角度误差较大，达到0.1 rad(5.7°)，稳态运行时角度观测准确。基于模糊PI的无传感器算法在动态升速过程中角度误差约为0.02 rad，同时稳态运行时位置观测准确。由此可得，改进算法能够兼顾动态与稳态下的位置估算精度并且几乎不存在高频噪声。

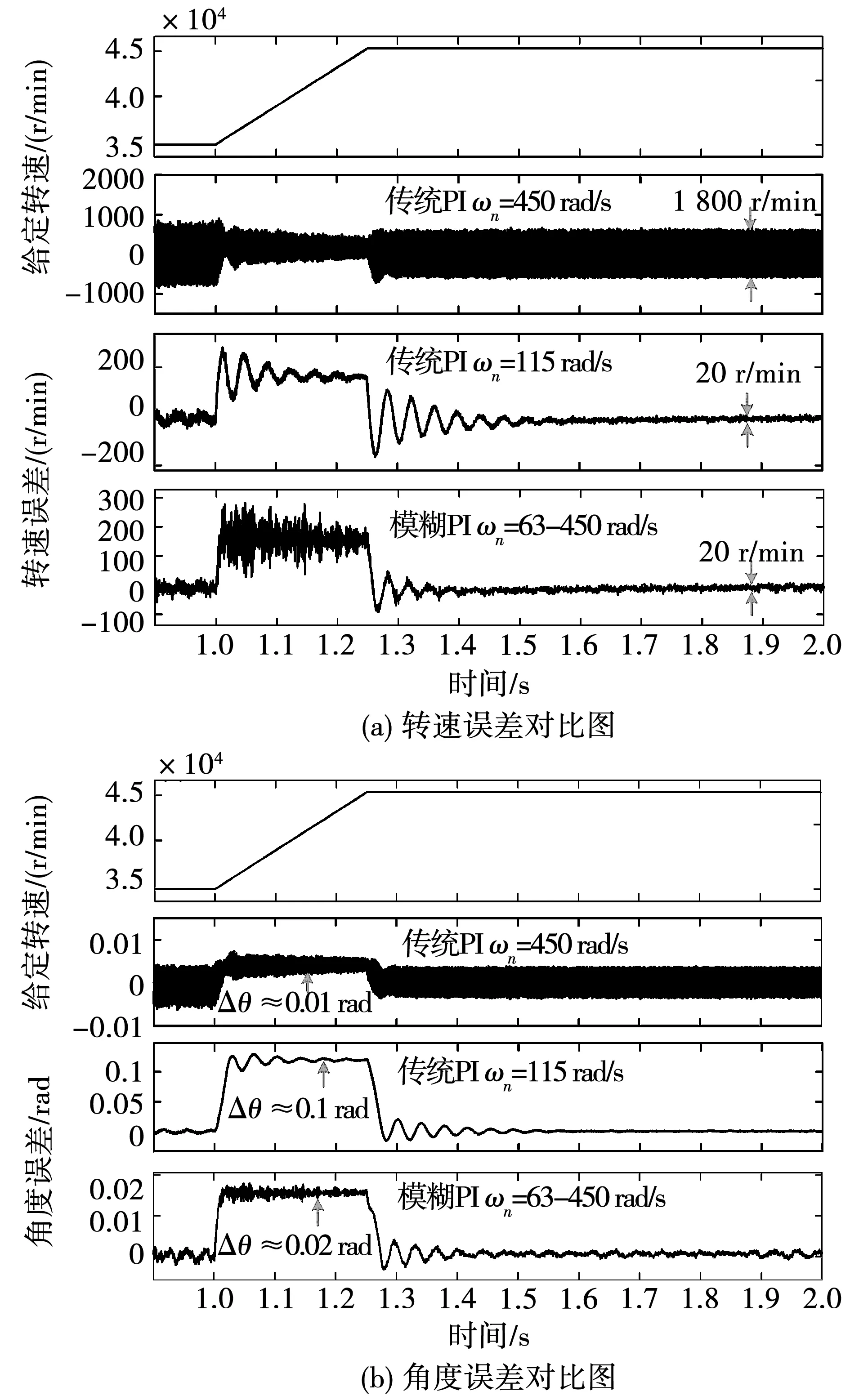
图12 传统PI与模糊PI对比图

5 实验结果

5.1 实验平台

在额定功率、转速分别为60 kW、45 000 r/min的电动环控用离心压气机上进行了验证实验。离心压气机电机如图13所示，最终的加载试验平台如图14所示。

图13 电动环控用高速永磁电机

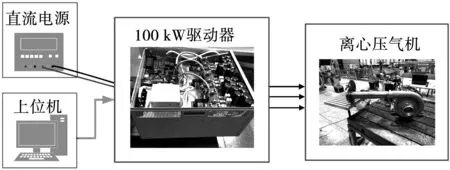
图14 加载试验平台

5.2 参数设计及算法验证

实验参数的选取基于理论推导，阻尼比ξ=1，自然频率变化范围在63≤ωn≤450 rad/s。空载状态下，给定速度从1 000 r/min升至20 000 r/min，上升斜率为10 000(r/min)/s，给定自然频率分别为ωn=115、215、315 rad/s，由图15可知在给定转速上升斜率不变的情况下，自然频率平方与动态升速时角度估计误差成正比关系。

当自然频率选为ωn=115 rad/s时，升速时角度误差约为0.12 rad(即8°)，转速稳定后波动控制在100 r/min。自然频率选为ωn=215 rad/s时，动态角度误差0.08 rad(即4.6°)，稳态转速波动也能够控制在100 r/min内，与理论相对应。随着自然频率的变大，当自然频率选为ωn=315 rad/s时，由图15(c)可知角度误差几乎为0，然而转速波动增大明显，高频噪声剧烈。进一步提高自然频率ωn至430 rad/s，系统出现了发散情况，与参数设计分析所得边界值有所差异，其原因在于仿真建模不够准确，未考虑实际存在的非线性因素。

图15 不同自然频率下转速与角度误差波形图

利用模糊PI代替位置观测器算法中的传统PI，实际转速与角度误差波形图如图16所示。图17为40 000 r/min下实际角度与估计角度对比图。最终能够保证在动态升速时角度误差控制在0.5°以内，并且稳态转速波动控制在±0.02%。

图16 模糊PI转速与角度误差波形图

5.3 带载实验

对该方法进行带风机类负载实验。电机额定转速为45 000 r/min，由于负载偏大，最终电机稳定运行在40 000 r/min，功率达到55 kW。图17为30 000、40 000 r/min下的估算角度波形、AB线电压波形、A相电流波形。

图17 实际角度与估计角度波形

图18 高速带载实验

6 结 论

针对基于假定坐标系的无位置传感器算法的参数设计方案进行了研究。提出了位置观测器传递函数与基于系统小信号模型的稳定性分析相结合的参数选取方案。利用分析所得参数特性制定模糊规则，提出具有参数自适应功能的假定坐标系下无位置传感器算法。所提改进控制策略有效降低了位置观测器参数调节难度，提高了系统动稳态性能。在高速大功率HSPMSM系统中进行了实验验证，证明了所提策略有效性。