基于改进漏磁能量系数法的分裂变压器穿越阻抗计算与分析
井永腾, 张永超, 孙荣锴, 曹靖琳, 李岩
(沈阳工业大学 国家稀土永磁电机工程技术研究中心,辽宁 沈阳 110870)
0 引 言
新能源工程正在全世界范围内建设和发展,而分裂变压器一机多能、安全环保、有效限制短路电流等优点,使其在光伏发电、海上风电和电力机车等新能源领域成为重要的变电设备[1]。分裂变压器短路阻抗的分布影响着变压器的抗短路能力、平衡性、效率、短路电流等。分裂变压器绕组为多端口电气网络,在轴向和幅向上,绕组结构不平衡、不对称,这导致了漏磁场的分布不规律。因此,采用现有的解析方法,很难对其短路阻抗进行计算[2]。
目前,短路阻抗的求解方法主要有漏磁链法,场-路耦合的有限元法,解析法及实验法等。漏磁链法方面,文献[3]由磁势平衡方程和相对磁势计算出等值漏磁面积,代入公式计算出阻抗电压。有限元法方面,文献[4-6]利用有限元软件,对变压器三维仿真分析,通过实验对比,得到了较为准确的数值。解析法方面,文献[7]推导了曲折接法的能量法公式,经计算具有相当的精度。最后,由于漏磁链法与解析法[8-10]计算短路阻抗误差较大,不适用于分裂变压器的计算。文献[11-17]用有限元法得到的仿真结果较为准确,但计算周期长,计算精度对人员水平要求较高,不利于新产品多方案进行对比。实验法由于产品成本较高,且不易发现机理性问题,一般不会采用。
因此,本文提出一种基于漏磁能量系数的方法,推导出分裂变压器的短路阻抗解析公式。该方法创新性的引入修正系数,填补当前分裂变压器短路阻抗解析计算的空白。同时,其精度满足工程要求且计算速度较有限元分析快,在满足工程设计要求的基础上,大大缩短变压器设计周期。采用该方法对一台十分裂干式变压器样机短路阻抗进行计算。同时,将计算结果与有限元仿真以及实验结果三者对比,对本文提出方法进行分析与修正,确立漏磁能量系数。最后,用一台型号为SFSZ9-40000 kVA /110 kV变压器验证该方法的可行性。
1 数字模型
本文采用漏磁能量系数法和基于有限元的漏磁能量法计算分裂变压器的短路阻抗。分裂变压器的线圈结构十分复杂,其绕制形式,排布方式和接线方式直接影响漏磁场及磁密幅值的大小,近而影响短路阻抗的平衡性。
以SGB10-800 kVA/6 kV十分裂变压器为例进行建模和仿真计算。模型如图1所示,根据电磁特性和结构对称性,对模型进行简化如下:
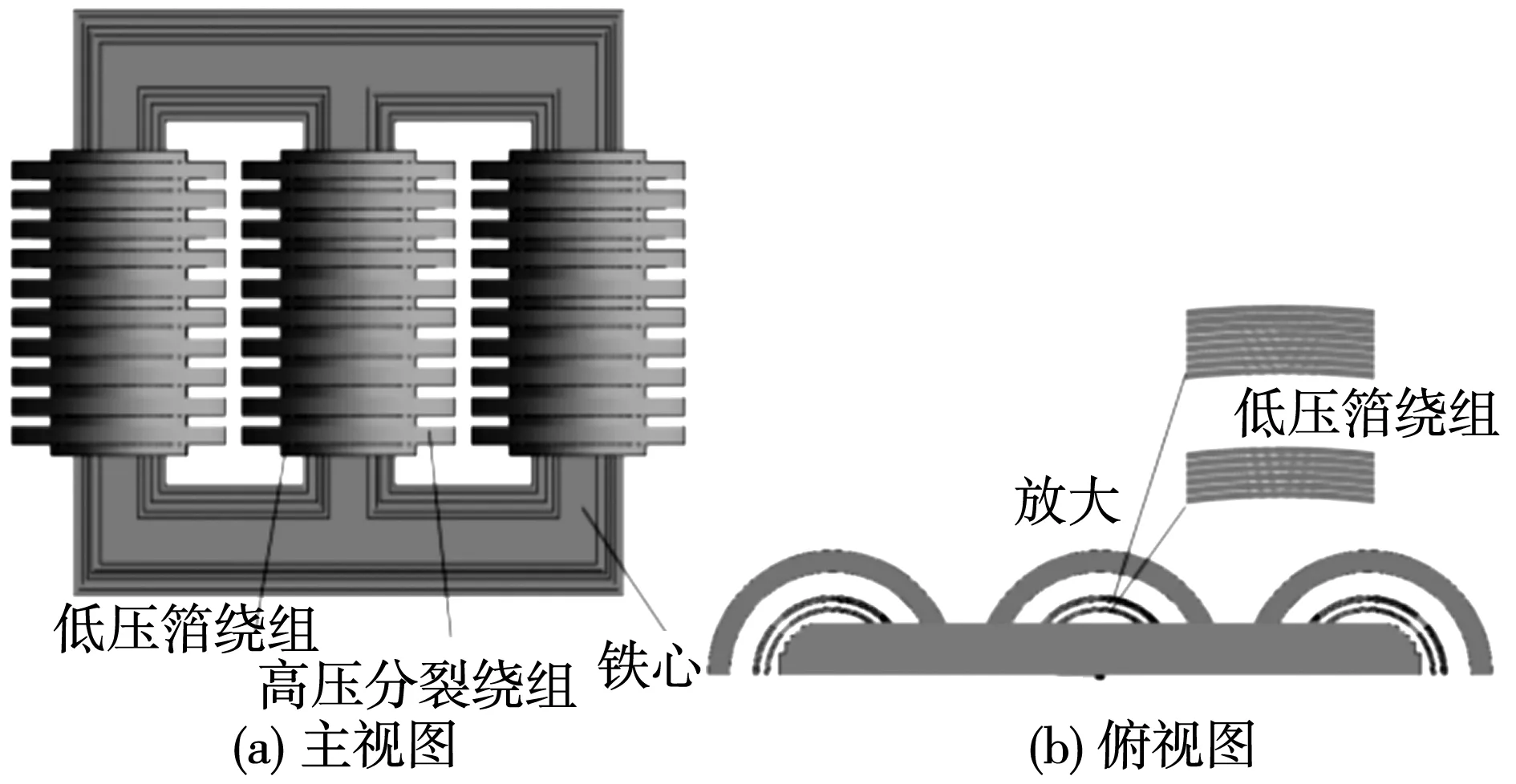
图1 变压器仿真计算模型
1)忽略涡流、环流和磁滞特性对磁场的影响;
2)所有场量正弦变化,忽略高次谐波的影响;
3)忽略引线和开关对磁场的影响。
变压器基本参数如表1所示。

表1 变压器基本参数
该台变压器铁心为三相三柱式结构,低压绕组采用的是箔式绕组方式,内层层数为6,外层层数为8,高压为饼式绕组,每饼线圈匝数为46。绕组结构为:铁心-低压绕组-高压10分裂绕组,绕组连接图如图2所示。

图2 绕组形式
1.1 漏磁能量系数法
正常绕组与轴向分裂式绕组均属于同心式绕组,其漏抗计算图如图3所示,由于磁阻是常量,漏磁通密度B呈阶梯形分布。

图3 同心式绕组示意图
同心式双绕组变压器磁动势方程为
I1N1+I2N2=I0N1。
(1)
式中:I1、I2为变压器一次、二次相电流;N1、N2为变压器一次、二次绕组的匝数;I1N1、I2N2为变压器一次二次绕组的磁动势;I0N1为励磁磁动势,建立主磁通Φ0,并与一次、二次绕组交链。
将式(1)数学变换,得到:
(2)
I1LN1+I2N2=0。
(3)
式中I1L为一次电流负载分量。
以上变换的意义是将变压器磁场分为主磁场与漏磁场,简化磁场计算。和为0的磁动势可产生漏磁场,变压器负载运行时,一、二次绕组磁动势平衡,即满足式(3)。
对于磁动势均匀分布的同心式双绕组变压器,内外层绕组之间的漏磁主空道上磁力线平行于心柱轴线,只在端部发生弯曲。由于励磁电流占一次电流比例很小,可近似忽略。因此一次、二次侧绕组磁动势可看作大小相等、方向相反[18]。
对于内层绕组,距离其内侧x处的磁密可以表示为
(4)
磁场能量可以表示为
(5)
对于内层绕组幅向所占空间单元体积为
(6)
式中h为变压器等高式绕组的高度。
内层绕组的磁场能量表示为
(7)
对于主空道,其磁通密度最大且均匀分布,主空道幅向占空间单元体积V=2πr12a12h,所以主空道的磁场能量表示为
(8)
由于外层绕组分裂,外线圈高度改正为hx,此时的主空道磁场能量改正为
(9)
对于外层分裂绕组所占空间,修改外层绕组高度为hx后,由式(9)同理可得,外层分裂绕组的磁场能量为
(10)
当分裂变压器内外绕组高度不相等时,考虑高度差引起绕组漏磁能量不平衡的影响,需引入一个不平衡率ρ作为系数,以保证内外绕组的高度近似相同。以等效漏磁场来代替实际漏磁场的情况,不平衡率的计算公式为
(11)
式中:n为变压器实际参与运行的分裂线圈个数;h1,…,hn为分裂绕组的物理高度;h1-2,h2-3…为分裂绕组间轴向距离;hx为参与运行的分裂绕组轴向漏磁高度。
各分裂绕组单独工作时,内外绕组高度相同但位置发生变化,各工况磁密大小分布不均匀,提出漏磁能量系数K来修正磁场能量,使其符合各个线圈单独工况下的磁密强度。由于内层绕组漏磁能量远小于主空道和外层绕组漏磁能量,可以直接用漏磁能量系数K修正最大漏磁能量Ww,进而简化计算。
K的解析式为
(12)
式中:hx1为内层绕组上端部到上铁轭的距离;hx2为外层分裂绕组上端部到上铁轭的距离;λ为分裂绕组半穿越时各工况下的穿越系数。其取值是通过对多个短路阻抗计算结果进行加权处理,得到的计算结果精确度大大提高,并通过实验验证来修正穿越系数。
考虑不平衡率和漏磁能量系数后,磁场能量相加,得
Wm=(Wn+Wk+Ww)ρK=
(13)
全穿越时,认为内外层绕组近似等高,由高度差产生的误差利用不平衡率ρ修正。半穿越时,参数代入式(13)中得到最大漏磁能量Wm,再代入漏磁能量法短路阻抗计算公式[18]中,计算整理后得到两种工况下短路阻抗。
全穿越工况时:
(14)
半穿越工况时:
(15)
1.2 漏磁能量有限元法
当运用基于T-Ω位组的漏磁能量有限元法对分裂变压器的短路阻抗求解时[19],变压器中储存的漏磁能量是在磁场建立过程中由外源做功转换而来的,因而计算出磁场的分布就可求出漏磁能量,近而可求得短路阻抗。当绕组中通有电流IN时,变压器磁场能量为
(16)
式中:L为变压器绕组电感;IN为变压器绕组相电流。
漏电抗为
(17)
式中ω为电源角频率。
短路阻抗为
(18)
式中:Uk为变压器短路阻抗百分数;ZN为变压器的额定阻抗;f为频率;U为额定电压;I为额定电流;SN为变压器额定运行情况下的容量。
2 计算结果分析
为验证公式的有效性,本文以变压器型号为SGB10-800 kVA/6 kV为例,通过提出的漏磁系数法和漏磁能量法对变压器分别建立十分裂、五分裂和二分裂模型。将模型参数代入公式计算出变压器全穿越时短路阻抗和变压器十分裂、五分裂、二分裂时,各个半穿越工况下的短路阻抗。
2.1 漏磁系数的选择
穿越系数λ为计算不同工况下的系数值,为简化计算,取平均值得到,如表2所示。不同工况下的穿越系数λ实际值对比如图4所示。
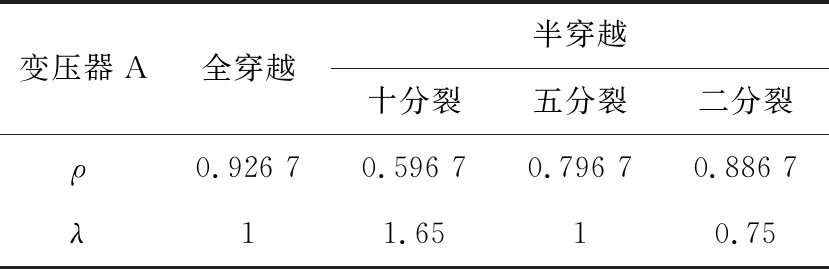
表2 变压器漏磁能量系数取值
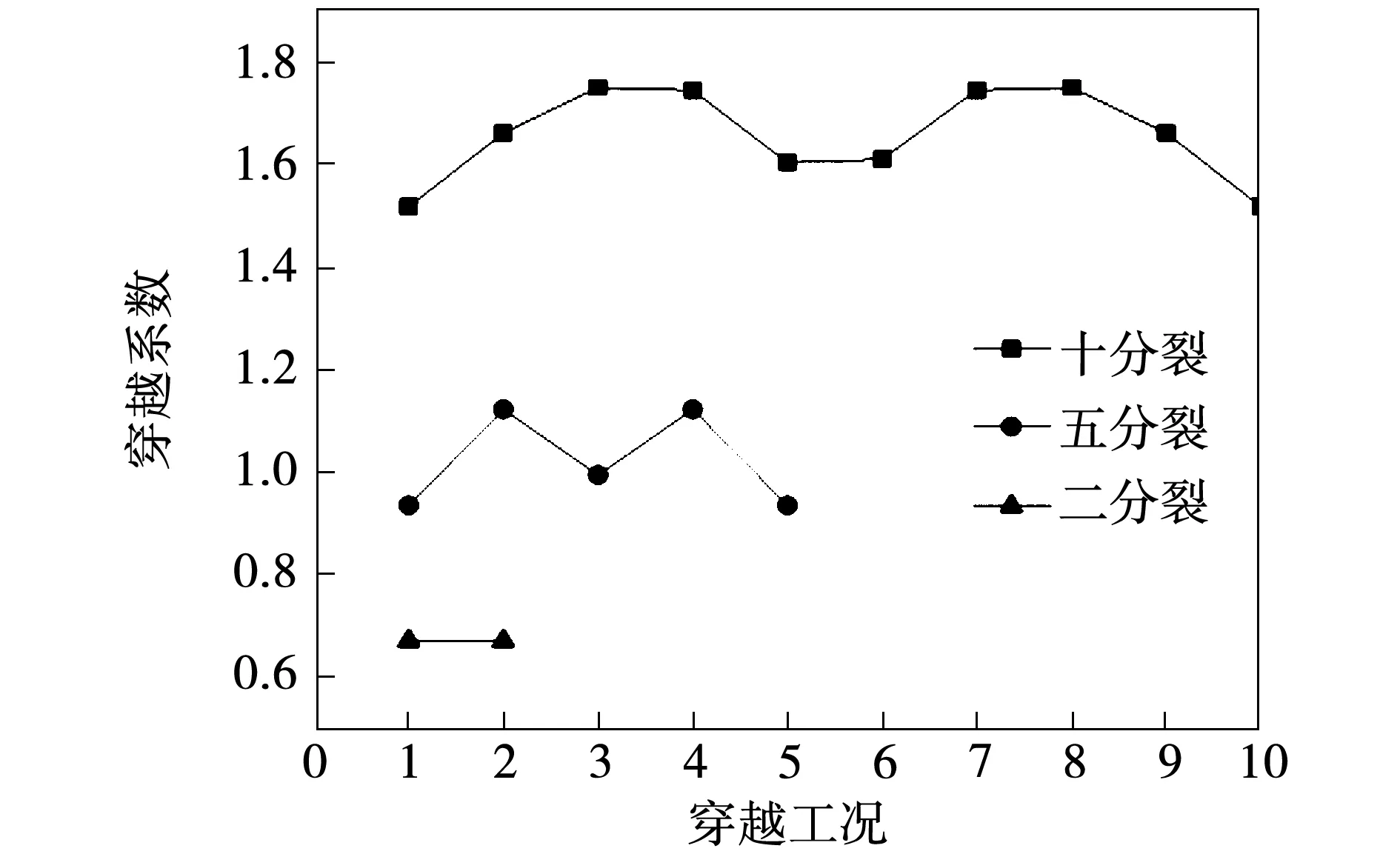
图4 不同工况下穿越系数对比
由图4可知,对穿越系数分析可知,分裂数越多,穿越系数的波动越大,变压器短路阻抗的变化越不稳定,为简化计算并提高短路阻抗计算结果的稳定性,对同一分裂但不同工况下的穿越系数取平均值进行计算。
2.2 漏磁能量系数法计算结果
基于本方法计算得到的能量值以及短路阻抗解析值如表3所示。由表可知,本文提出的计算方法误差在±5%以内,优于传统的解析法,满足工程需要的同时,计算速度快、精确度高。不论产品容量和电压等级为多少,只要结构相同,就可以用此方法进行计算。

表3 漏磁能量系数法结果对比
2.3 漏磁能量有限元法计算结果
基于漏磁能量有限元法仿真得到的能量值以及短路阻抗值如表4所示。有限元法计算漏磁能量时,越复杂的模型,需要剖分网格越精细,所需变压器设计时间更长。适合作为变压器精细计算及优化分析。

表4 漏磁能量有限元法结果对比
铁心是变压器磁路的重要组成部分,当相角为60°时,变压器不同工况下的铁心磁通密度分布如图5所示。可以看出各工况下铁心磁通密度的最大值都出现在铁心柱与铁心上下轭接缝处,十分裂全穿越时主磁通密度幅值在0.077 T左右,十分裂LV-HV1工况时主磁通密度幅值在0.211 T左右,五分裂LV-HV1工况时主磁通密度幅值在0.334 T左右,二分裂LV-HV1工况时主磁通密度幅值在0.487 T 左右,说明半穿越工况时绕组端部漏磁比较大。

图5 不同工况下铁心磁密
漏磁能量主要分布在内层绕组、主空道和外层绕组中。其中,内层绕组和外层绕组的漏磁能量最小,主空道漏磁能量最大。对变压器短路阻抗的影响也最多。十分裂全穿越和LV-HV1工况下的主空道的磁密曲线如图6、图7所示。
由图6可知,由于分裂绕组间存在间隙,导致漏磁场在间隙处和绕组空道处磁密强度呈波峰波谷状,磁场分布不均匀,存在锯齿状波动。由图7可知,线圈1单独工作时,磁力线闭合距离远,磁密强度在线圈空道处的分布呈峰值状态,磁密强度波峰位置对应线圈1的位置。

图6 十分裂全穿越工况下主空道磁密曲线

图7 十分裂LV-HV1主空道磁密曲线
3 实例计算与分析
本文对一台十分裂变压器进行了全穿越和半穿越短路阻抗实验,十分裂变压器样机如图8所示。测试方法主要通过SYBS-2310变压器综合实验平台输入变压器基本参数,对输入激励大小进行控制,对其稳态下的额定电流,电压以及阻抗值进行实时记录和监测。通过更改外电路接线对各个运行工况下进行实验,得到准确的短路阻抗值。

图8 实验样机
3.1 试验研究
综合实验平台如图9所示,接线方法为对低压侧箔式绕组a、b和c三项用铜排短接,全穿越工况时,10个线圈全部接入电路中,施加额定电流的幅值。半穿越工况时,通过改变接线柱上的连接分别将每个线圈接入电路中,施加额定电流的幅值。

图9 综合实验平台
图10为实验现场图,监测高压侧电流达到额定值一段时间后,短路阻抗几乎不发生变化,开始记录数据。并重复操作,改变接入电路的分裂绕组数,记录数据。
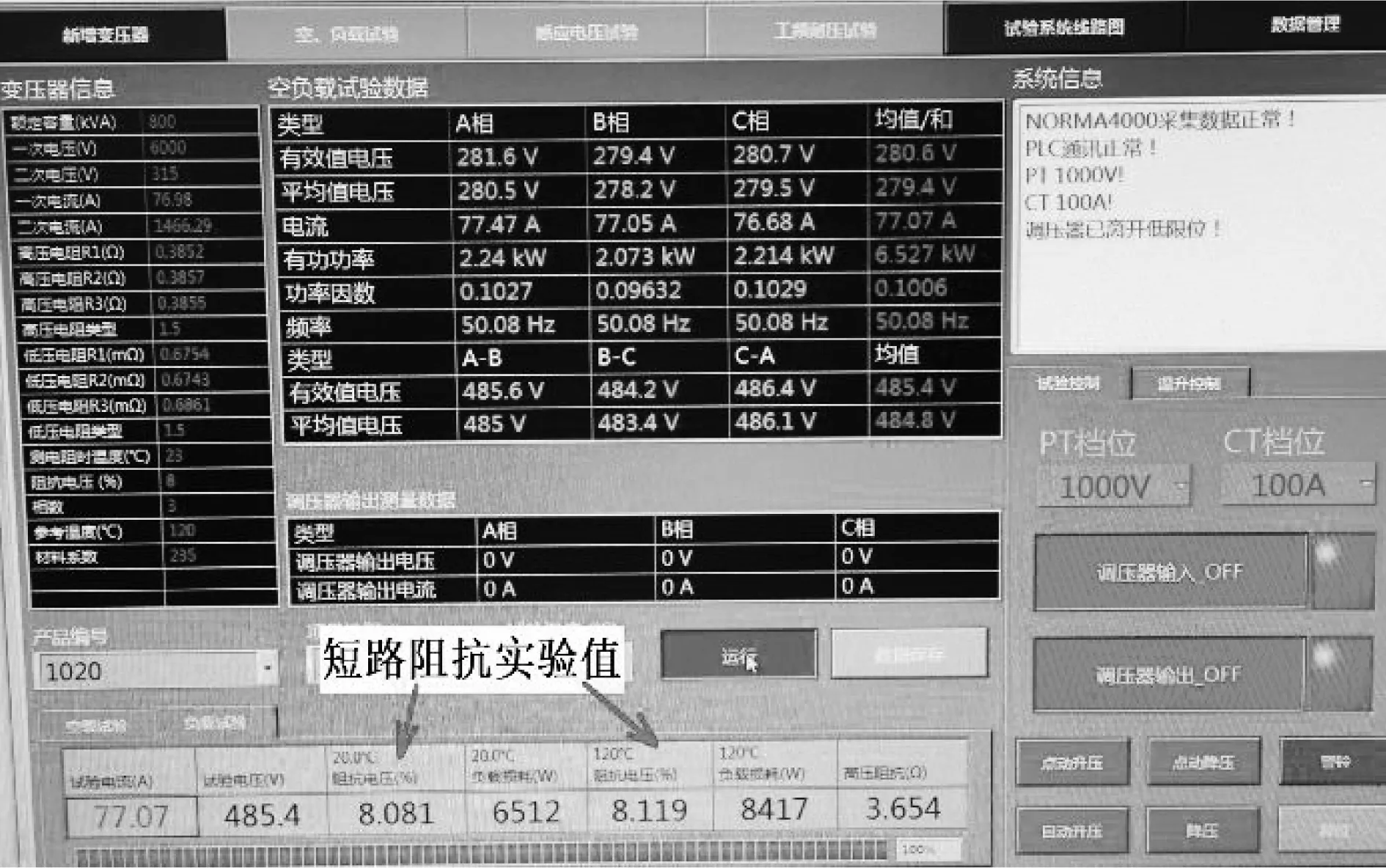
图10 实验现场图
3.2 曲线对比
利用小波包对数字孪生变压器推演的大量数据样本号进行3层分解,其分解结构的能量分布(%)如图11所示。
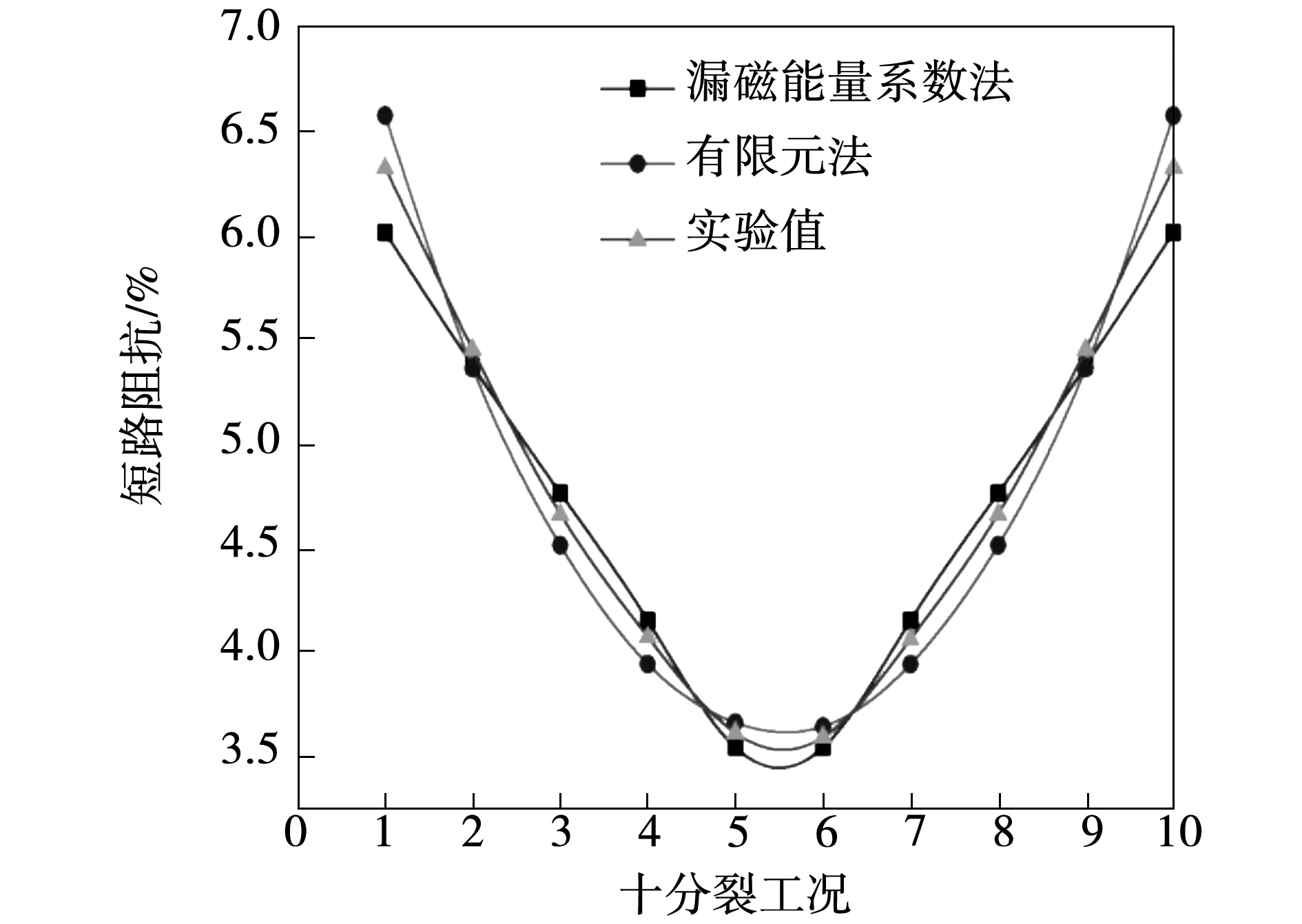
图11 十分裂各工况下阻抗值对比图
由图可知,由于分裂线圈的周围磁场分布不均匀且轴向存在对称性,线圈1~10分别单独工作时,漏磁系数法及有限元法计算出能量值呈先减小后增大的趋势。处于端部的线圈磁力线易发散,漏磁大;处于中间部分的线圈磁力线更容易闭合,漏磁小。近而短路阻抗计算值呈近似U形,上半部分与下半部分对称。
漏磁系数法在各工况下计算的阻抗值曲线趋势较陡,计算精度在各工况也并不相同;漏磁系数法与有限元法计算结果的最大误差均出现在端部,漏磁系数法最大误差4.94%,有限元最大误差3.64%,最大误差均小于5%,满足工程需求。
3.3 漏磁能量系数验证
为论述详实,选用另一台型号为SFSZ9-40000 kVA/110 kV电力变压器进行了仿真验证,变压器具体参数如表5所示。

表5 变压器基本参数
通过实验对比可知,采用本文选取的穿越系数,短路阻抗的解析计算结果与实验结果较为吻合,因此,本文所例举的穿越系数选取方法是正确有效的。

表6 变压器漏磁能量系数取值
4 结 论
本文提出了漏磁能量系数方法解决了当前方法对分裂变压器短路阻抗计算不准确、计算周期长的问题。为后续计算方法的优化提供思路。得到结论如下:
1)推导漏磁能量系数法公式,并由实验确定漏磁能量系数,采用本文方法对分裂变压器短路阻抗进行计算,全穿越短路阻抗值为8.48%,误差值小于5%,经另一台二分裂变压器验证,误差值为1.15%,满足工程设计需要。
2)采用有限元法计算短路阻抗,全穿越时短路阻抗为8.15%,误差为0.87%;半穿越时,LV-HV1阻抗最大为6.57%,LV-HV6阻抗最小为3.64%,工况1~工况5阻抗值逐渐减小,且与工况6~工况10阻抗值基本对称;有限元法最大误差为4.71%。
3)通过变压器全穿越与半穿越短路阻抗实验,全穿越实验值为8.081%,半穿越实验值分布情况与仿真值和本文所提解析法计算值基本符合。
经多台产品实验验证,本文提出方法合理有效。本文提出的方法克服了传统解析方法计算不准确的问题,在满足工程设计要求的基础上,大大缩短了变压器设计周期。

