一种单级无桥Sepic_LLC变换器及其滑模控制
徐玉珍, 万陆峰, 金涛, 萧展涛
(1.福州大学 电气工程与自动化学院,福建 福州 350108;2.福建省新能源发电与电能变换重点实验室,福建 福州 350108)
0 引 言
为减少电网污染,电力电子驱动电源多包括功率因数校正(power factor correction,PFC)级和功率变换级[1-3]。两级式AC-DC变换器虽然在提高功率因数和降低总谐波因数方面取得良好的效果,但在中小功率应用场合,存在体积大、效率低、控制复杂等问题。而单级AC-DC谐振变换器,由于只需一套控制电路,在系统可靠性、电能转换次数、变换器效率有较大的提升,尤其适合于中小功率应用场合[4-8]。
单级LED驱动电源前级通常选用Boost、Buck-Boost 等变换器,而后级选用Buck、Flyback、LLC等变换器进行集成。其中后级电路若采用LLC谐振变换器进行集成时,不仅能获得较低的THD(total harmonic distortion)和较高的PF(power factor)值,而且能保留LLC谐振变换器软开关特性,从而提高单级AC-DC变换器的整体效率。
传统单级Boost-LLC谐振变换器由于一直工作于升压模式,易导致母线电压过高,开关器件电压应力过大等问题,通常应用于低压输入场合,应用范围较小。而当前级采用Buck-Boost电路时,虽然能够扩宽输入电压的应用范围,但输入电流存在死区,对THD、PF值等输入特性有不利的影响。相比于其他变换器,Sepic变换器能够工作于升降压模式,因此单级Sepic_LLC变换器母线电压较低,一般仅大于输入电压峰值,更适合工作在宽范围输入电压场合。当Sepic变换器工作于不连续导通(discontinuous conduction mode,DCM)模式时,变换器还具有优化输入电流谐波和通过单电压环实现PFC等优点[6]。
LLC变换器传统控制方法为脉冲频率调制(pulse frequency modulation,PFM)控制,开关管占空比为固定值(0.5)。PFM控制虽然简单,但应用于单级AC-DC谐振变换器中,由于变换器PFC部分始终工作于升压模式,无法对直流母线电压变化范围进行控制。尤其在高压输入下时,会给变换器中开关器件和母线电容带来较大的应力。因此,较为合适的方法是对母线电压进行控制[9-10]。宽范围输入时,现有混合控制策略在稳定母线电压时,往往难以兼顾输入特性,同时基于母线电压输入前馈的混合控制策略存在带宽受限、参数设计难等问题。
文中研究一种单级无桥Sepic_LLC谐振变换器。前级采用可用于输入电压高场合具有升降压功能的Sepic变换器实现功率因数校正;后级采用LLC谐振变换器,以实现软开关特性,提高系统效率。针对该变换器,文中研究一种滑模变占空比控制策略。通过详细分析工作于DCM模式时无桥Sepic输入输出特性,基于比例切换滑模控制原理,选择合适的滑模面变量建立控制函数,使母线电压稳定在一定范围的同时保持良好的输入特性。文中对单级无桥Sepic_LLC谐振变换器及滑模变占空比控制策略的工作原理进行详细理论分析,并通过仿真和实验研究进行验证。
1 单级无桥Sepic变换器工作原理
本文提出的单级无桥Sepic变换器如图1所示。其中无桥Sepic-PFC部分由交流输入电源vin,电感L1、L2,二极管D1~D3,电容C1和母线电容Cbus以及开关管S1、S2构成;LLC电路由二极管D4、D5,开关管S1~S3,谐振电容Cr,谐振电感Lr,高频变压器T、二极管Do1、Do2和输出电容Co构成。通过开关管S1、S2的复用,无桥Sepic-PFC单元与LLC单元构成单级AC-DC谐振变换器。
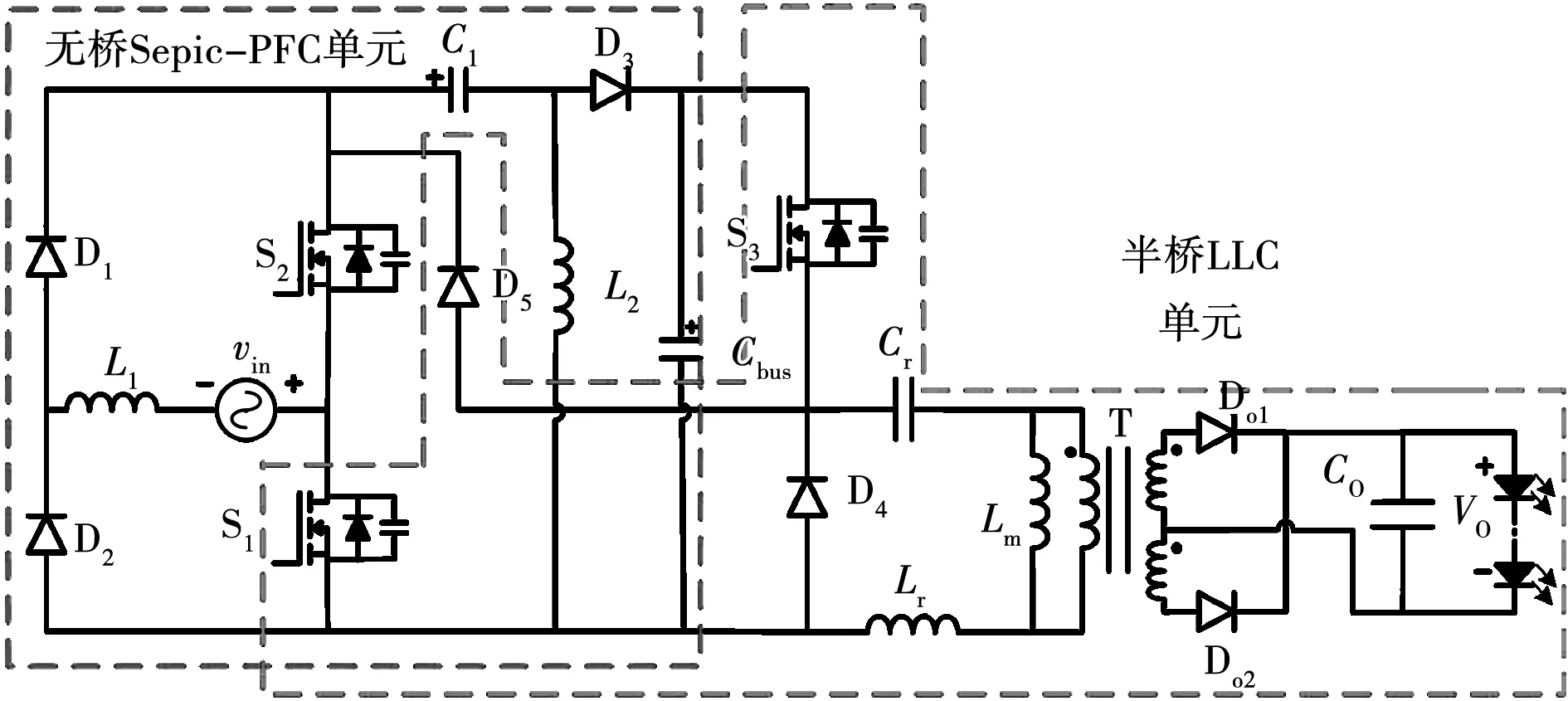
图1 单级无桥Sepic谐振变换器
为简化电路分析,现作如下说明:
1)开关频率远大于交流输入频率,在每个开关周期Ts内交流输入电压、输入电流为一定值;
2)C1的电压在每个Ts内跟随交流输入电压;
3)Cbus和Co足够大,每个Ts内电容电压恒定;
4)无桥Sepic-PFC工作于DCM模式,以D3电流持续过零作为判断标准。
基于交流输入电源正负半周工作原理相同,此处仅以正半周为例进行说明。根据LLC变换器工作特性,存在两个谐振频率fr1、fr,其表达式为:
(1)
LLC变换器的工作频率fs处于3种变化区间
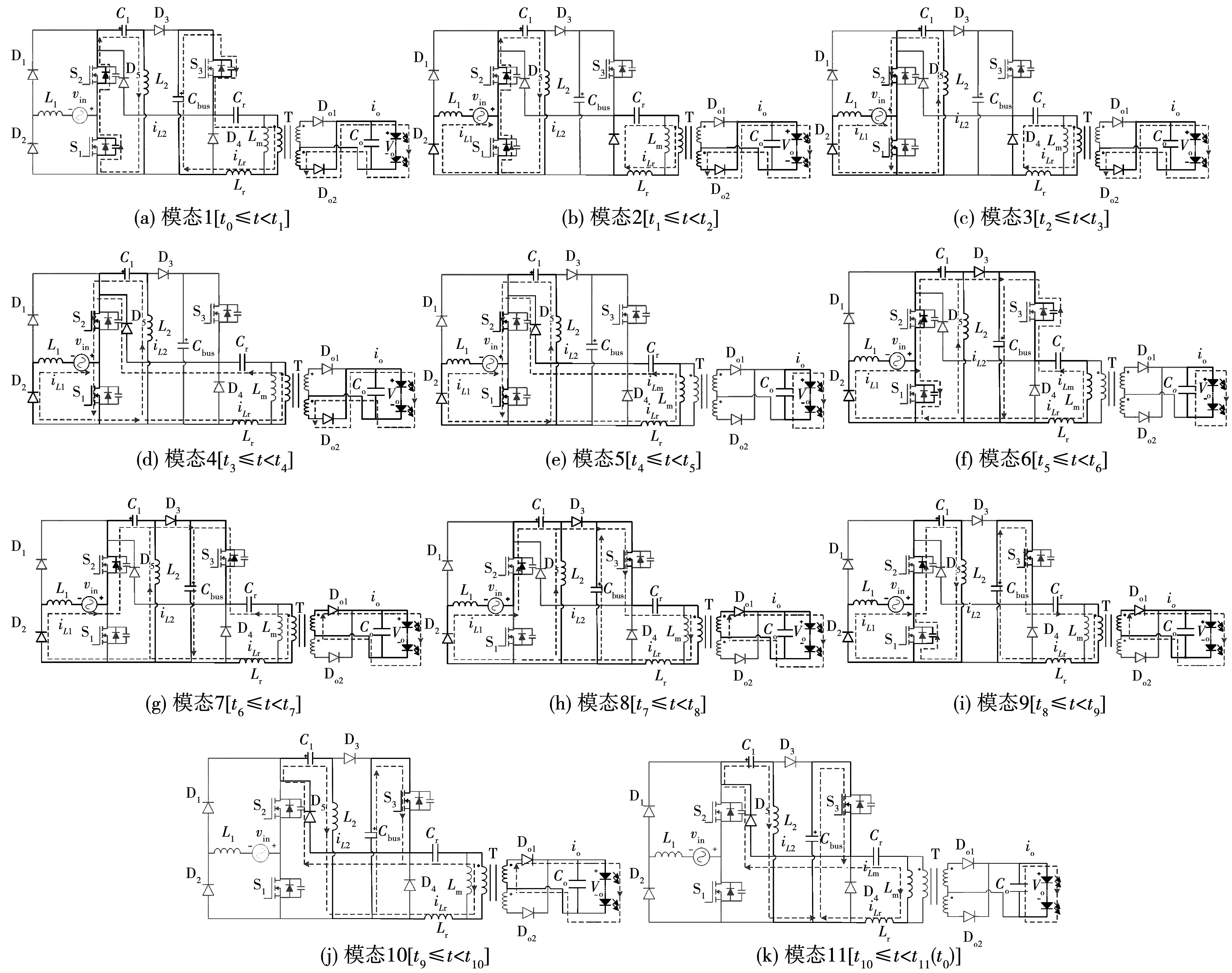
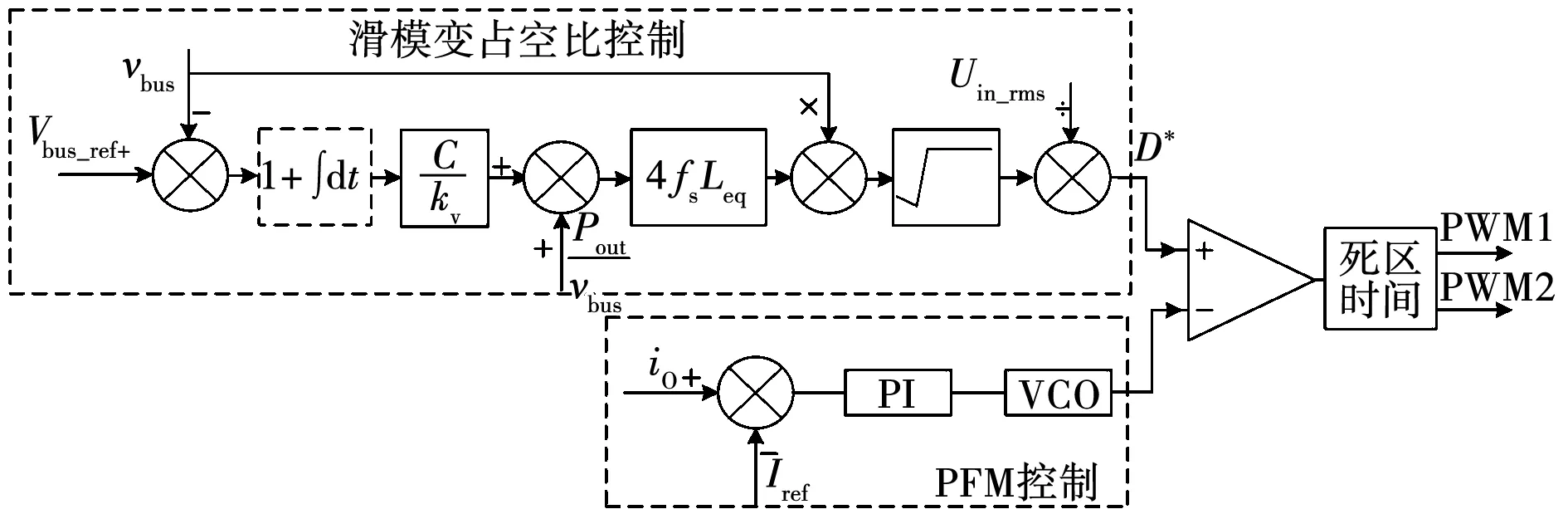
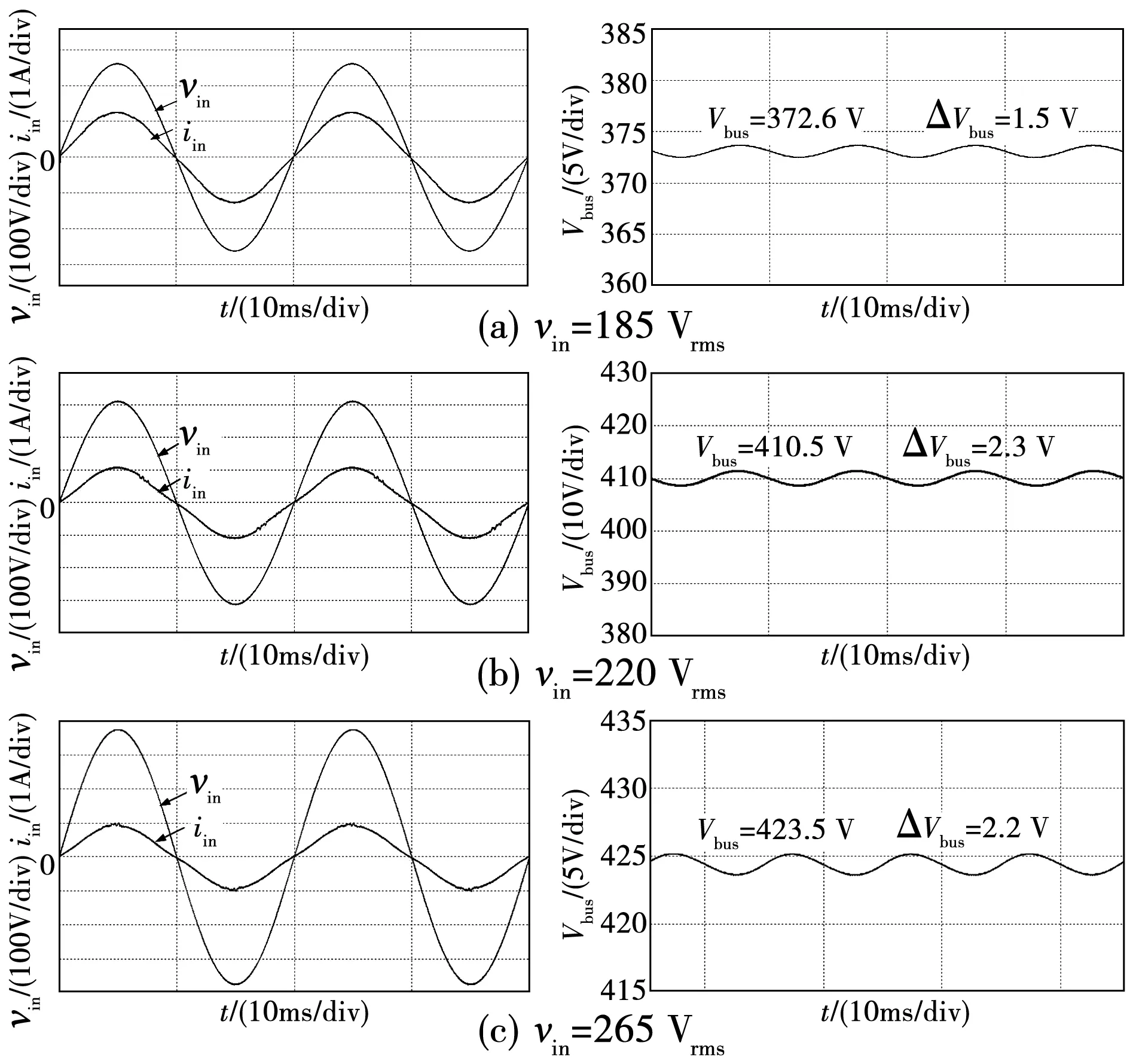
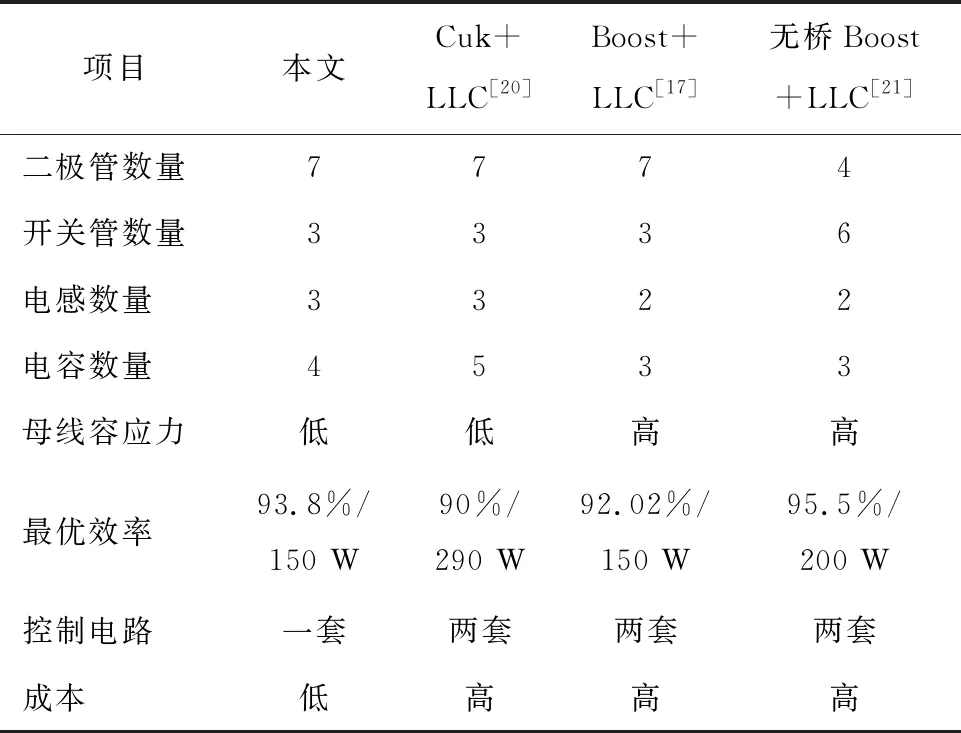
内,分别是fr1 图2 关键工作波形 模态1[t0≤t LLC变换器中,S3的结电容由谐振电流ir进行充电,Do2导通,由于Lm两端的电压被输出电压Vo所箝位,没有参与谐振,励磁电流iLm线性下降,表达式为 (2) 式中:n为变压器原副边匝比;Vo为输出电压。 ir(t)表达式为 ir(t)=Ir_pksin[ωr(t-t0)+θ]。 (3) 式中:Ir_pk为谐振电流峰值;ωr=2πfr;θ为谐振电流相角,定义[11]为: (4) 模态2[t1≤t (5) LLC电路中,ir方向不变,S3结电容充电至母线电压,二极管D4、Do2导通,谐振腔工作状态同模态1相同。此阶段中ir不经过各开关管。 模态3[t2≤t 模态4[t3≤t (6) 模态5[t4≤t (7) 流经S1、S2的各电流关系仍与模态4中相同。 模态6[t5≤t 图3 所提变换器工作模态 (8) D3中流过的电流为 iD3=iL1+iL2。 (9) ir对S3的结电容放电,为其实现ZVS做准备。此时谐振腔中电流的流向和副边电流流向均与模态5相同,iLm表达式也和模态5中一致。 模态7[t6≤t (10) 谐振电流表达式为 ir(t)=Ir_pksin[ωr(t-t6)+θ]。 (11) 模态8[t7≤t 模态9[t8≤t 模态10[t9≤t (12) LLC电路中,谐振腔的工作状态均和模态9相同,该阶段持续至ir和iLm相等,Do1实现ZCS。 模态11[t10≤t (13) t11时刻,此时相当于t0时刻,S3关断,稳态时以上各模态工作过程不断重复。 综上所述,当fs工作于fr1 根据上述电路模态分析,由于变换器在交流输入正负半周时对称工作,而S1、S2分别在关断时,正负半周内承担续流二极管的作用,所以在交流输入正半轴内,S2在关断时其体二极管一直作为续流二极管工作,因此其上电压为0,综合以上电路模态分析,变换器中开关器件的电压应力如下: 1)开关管S1、S2、S3的最大电压应力为: (14) 2)二极管D1~ D5、Do1、Do2最大反向电压应力为: (15) 式中Vm_max为交流输入电压最大值。 本文提出的单级无桥Sepic谐振变换器的无桥Sepic-PFC电路部分如图4所示。 图4 无桥Sepic-PFC变换器 在开关周期内,以工频周期内正半周为例,该电路处于DCM模式时,变换器有3种工作模态,关键参数波形如图5所示,等效电路如图6所示。 图5 DCM模式无桥Sepic-PFC变换器关键波形 图6 无桥Sepic-PFC变换器工作模态 由Sepic变换器的工作特性可知,C1在开关周期内的电压值近似等于输入电压值,当电感L1=L2时,两者电感上升和下降速率相同。 为了进一步分析变换器的工作特性,图5给出了DCM中L1、L2电流和二极管D3电流的理想波形。D3的电流峰值iD3_pk为: (16) 式中:vin为交流输入电压;ifw为D3电流断续时流过L1与L2电流的大小;α1为S1(S2)导通占空比;Leq为无桥Sepic-PFC等效电感。 根据电感伏秒平衡特性,可将占空比描述为: (17) (18) 式中:α2为D3导通占空比;Vo为输出电压。 根据图5所示D3电流波形,结合式(17)和式(18)可以推出D3在一个开关周期内的平均电流表示为 (19) 式中Vm为交流输入的峰值电压。 理想情况下,在一个开关周期内储能元件不耗能,根据功率平衡,可得输入电流为 (20) 将式(19)代入式(20)中可得出 (21) 由式(21)可知,当α1固定时,工作于DCM的无桥Sepic-PFC中的输入电流iin为正弦波,与vin的频率和相位一致。这使得控制系统可以在输入侧自动实现PFC功能,而不需要输出随输入电压而变化的占空比,在两个电感的联合调节下具有良好的谐波性能。此时,控制系统的任务是输出一个理论上恒定的占空比,以保持输出电压跟随参考值。因此,可以通过使用单个电压回路来实现控制目标。 传统PI电压环控制器,是利用输出电压的误差来调节占空比,直至达到稳态。基于PI控制器的单电压环虽然实现简单,但在PFC电路中使用的带宽有限,动态响应速度慢。另外,当没有电流环控制时,单电压闭环控制系统受外界干扰和系统参数的影响很大。同时,PI控制器的参数设计仍然比较复杂。 相比于PI控制,滑模控制首先对变换器数学模型的强非线性具有良好的适应性,即在一定程度上降低了对数学模型本身的要求[12-14];其次,滑模控制变量具有对外部干扰和系统参数变化不敏感的优点,这更有利于提高变换器的直流输出电压的稳定性、DCM模式下的响应速度和抗干扰能力;最后,滑模控制策略的实现条件比较简单,在仿真中易于构建和调试,在硬件中也易于实现。 滑模控制的基本设计对象包括滑模面变量、滑模函数和控制律。在传统的设计方法中,经常选择跟踪物理量x1和跟踪速度x2作为状态变量,将这两个变量与实际参考值的误差值作为滑动面变量,即 (22) 滑动模态函数可定义为 (23) 式中c为滑动模态函数中状态变量的跟踪物理量系数。 当s=0即到达相应的滑动面。可以看出在滑动面两侧滑动时,误差的平均值及其跟踪速度应为0。这表明系统已经达到稳态,处于动态平衡的过程中。 对于非线性系统(如开关电源),由于高频开关工作状态,开关的动作可以作为等效控制实现系统的运动状态两边的滑动面,这本质上是一种间接滑模控制[13-14]。为方便对所提出变换器进行控制,并使LLC谐振腔工作在相对稳定的状态,需要对母线电压进行控制,即在Sepic_LLC变换器中被跟踪的状态变量是母线电容输出电压。因此,母线电容输出电压的跟踪误差和跟踪速度(即误差变化率),这些都为滑动面变量,所以系统变量和相应的滑模函数被定义为: (24) s=e1+kve2=(Vbus_ref-vbus)+ (25) 式中kv为滑模函数中状态变量的跟踪速度系数。 上式中PFC输出电压参考值的变化率可视为0。因此,可以对PFC输出电压变化率进行分析,利用母线输出电容及其电流关系式可以得出PFC输出电压变化率的表达式,根据前述理论分析可知,输出电容电流为D3在开关周期Ts下的电流平均值与输出电流的差值,即 (26) 将式(19)、式(26)代入式(25)中可得到滑模面函数为 (27) 当滑模面到达时,滑模函数s=0,即可以得到α1关系为 (28) 对于Sepic_LLC变占空比控母线电压,其等效滑模控制可以设为 (29) 式中:D*为变换器滑模控制等效占空比;kv作为滑模函数中状态变量的跟踪速度系数,对滑模控制系统的效果有一定的影响。它也是Sepic_LLC滑模控制策略中唯一需要设计的参数。一般来说,在合理范围内,kv值越小,跟踪速度越快,跟踪精度越好。而在稳定状态下,由滑动运动引起的抖振会更加严重。为了抑制固有抖振,可以选择较大的kv值,但代价是降低响应速度。对于无积分滑模控制,常存在稳态误差,即输出电压不能准确跟踪给定值。为了减小稳态误差,引入了误差信号的积分作为其中的状态变量[15-16]。带积分的改进滑模面函数为 (30) 积分滑模控制消除稳态误差的效果与PI控制器相似。而PI控制器中积分部分和比例部分的参数相互影响,调节系统的开环频率特性。积分滑模控制中的积分元件对其他控制部分影响不大,只是为了消除稳态误差。通过以上分析,最终得到的Sepic_LLC滑模控制结构图如图7所示,滑模变占空比控制中虚线部分包含引入的直流输出电压误差积分状态变量。 图7 Sepic_LLC滑模控制结构图 由图7可知,将采样输出电流io和参考值Iref进行比较,电流误差经过PI补偿环节后送入压控振荡器输出得到PFM信号。滑模变占空比控制只需采集母线电压vbus和输出功率Pout,其逻辑运算框图如图7所示。占空比数值与通过PFM控制得到的信号进行比较后添加固定的死区时间最终得到PWM1、PWM2的控制信号。 为了保证母线电压大小适中,同时避免滑模动作过于频繁而导致颤抖,当母线电压达到目标范围时(设定为370~430 V),固定占空比,LLC工作状态为传统的PFM控制;当母线电压在设定电压范围以外时,为了稳定母线电压,滑模变占空比动作,变换器工作状态为混合控制(APWM-PFM)。 为了验证理论分析,利用PSIM仿真软件对所提出变换器和控制策路进行仿真研究,变换器主要参数如表1所示。 表1 变换器主要参数 在满载条件下,图8为不同交流输入时,经滤波后的输入电流iin、输入电压vin波形和母线电容上电压Vbus的波形。 图8 不同交流输入电压时,vin、iin以及Vbus的仿真波形 由图8可知,iin能够良好地跟随vin,且iin的正弦度较高,即在宽范围交流电压输入条件下,变换器仍具有良好的输入特性,无桥Sepic-PFC较好的实现了PFC功能。同时,Vbus始终稳定在370~430 V之间,即滑模变占空比控制能有效地对Vbus进行控制,且没有对电路的输入特性造成不良影响。 在额定输出功率下,图9为不同交流输入185~265 V时,变换器的软开关特性波形和谐振电流波形。由图9可知,各开关管均实现了ZVS,副边二极管也工作在ZCS状态下。 图9 不同交流输入电压时,变换器的软开关特性波形 基于DSPF28335数字控制平台,搭建一台实验样机,其性能指标如下:vin有效值为185~265 V;满载输出功率为150 W;实验样机主要参数如表1所示;实验样机如图10所示。 图10 实验样机 在宽范围交流输入电压的条件下,变换器经滤波后的输入特性和母线电容上电压的波形如图11所示。 图11 不同交流输入电压时,变换器的输入特性和母线电压的波形 图12为实验样机与传统两级式变换器[17]和单级Boost-LLC交直流变换器[18]、低母线电压单级LLC变换器[19]的实测功率因数(PF)、总效率随vin变化的对比曲线。由图可知,样机的PF值、效率整体上都高于文献[17-19],这表明本文所提单级无桥Sepic_LLC谐振变换器及滑模变占空比控制策略具有更好的性能。 图12 PF、效率η随vin变化的对比曲线 由图12和图13可知,在满载情况下,在vin为185 Vrms时,Vbus为375.8 V,此时变换器PF值为0.998,THD为4.8%;在vin为220 Vrms,Vbus为402.6 V,此时PF值为0.997,THD为5.7%;在vin为265 Vrms时,Vbus为416.5 V,此时PF值为0.997,THD为7.2%。由图11中可知,经滤波后iin能够良好地跟随vin,且iin的正弦度较高,电路具备良好的输入特性,无桥Sepic-PFC单元较好地实现了PFC功能,且从母线电容电压波形可知,滑模变占空比控制策略有效地控制了母线电压,Vbus总体变化范围在60 V以内,使谐振腔工作在一个较好的输入电压范围。 图13 THD随vin变化的曲线 在额定输出功率下,当变换器工作处于稳态时,在整个vin范围内,样机PF值均高于0.995,THD均低于8%。同时,在vin有效值分别为185、220和265 Vrms时,对iin做傅里叶分解,其各次谐波含量如图14所示,由图可知,iin的分解后的各次谐波含量均低于标准IEC61000-3-2 Class C标准值。 图14 不同交流输入电压下,iin各次谐波含量与标准比对 如表2所示,本文提出的单级式变换器相比传统两级式变换器只需要一套控制电路,控制复杂度和成本更低;相比传统两级式有整流桥变换器,效率更高;相比两级式无桥Boost_LLC变换器,所需开关管更少,母线电容电压应力更低。 表2 本文变换器与传统两级式变换器对比 满载情况下、不同vin时,谐振电流ir波形如图15所示。由图可知,对于LLC变换器来说,随着vin的增加,为了减小直流母线电压变化范围,开关管占空比不对称加大,即ir不对称越明显。 图15 不同交流输入电压时,ir波形 在额定输出功率下,图16为不同vin下,开关管S1、S2、S3的漏源极电压vds、驱动vgs及漏源极电流ids波形。从实验结果可以看出,在不同vin下,滑模APWM-PFM混合数字式控制策略没有破坏开关管的软开关特性,开关管均实现了ZVS。图17为变换器在Po=120 W条件下,不同vin下各开关管的vgs、vds及ids波形,从图中可以看出各开关管也都实现了ZVS。 图16 满载、不同交流输入电压下,vds、vgs、ids实验波形 图17 Po=120 W时、不同vin下,vds、vgs、ids实验波形 由图18可知,在满载情况下,不同vin有效值时,次级整流二极管iDo、电压vDo波形。在vin为185~265 Vrms时,电路开关管频率都工作在fr1 图18 不同交流输入电压时,副边二极管电流、电压波形 文中研究了一种单级无桥Sepic-LLC变换器和一种滑模变占空比控制策略,通过理论分析、仿真和实验研究得到如下结论: 1)文中提出了一种单级无桥Sepic_LLC变换器。理论分析、仿真和实验结果均表明:通过无桥电路结构减少了导通损耗。在器件数目、控制复杂度、成本等方面优于传统两级式变换器。 2)文中设计了一种滑模变占空比控制策略。理论分析、仿真和实验结果均表明:该控制策略有效解决了传统PFM控制策略所带来的的母线电压过高和变化范围大等问题,并保留了变换器的软开关特性。 3)仿真和实验表明变换器功率因数均在0.99以上,THD均在8%以下,母线电压降低且电压纹波减小,避免了高压输入下的器件损坏,降低了所需母线电容的电压等级和容量。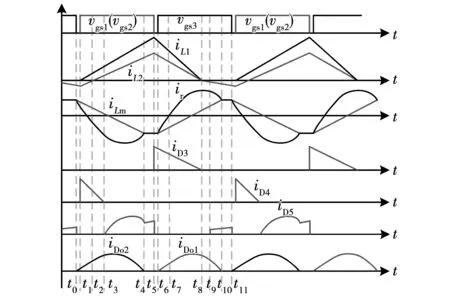
2 无桥Sepic电路PFC原理



3 无桥Sepic_LLC滑模变占空比控制律设计
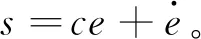

4 仿真结果与分析
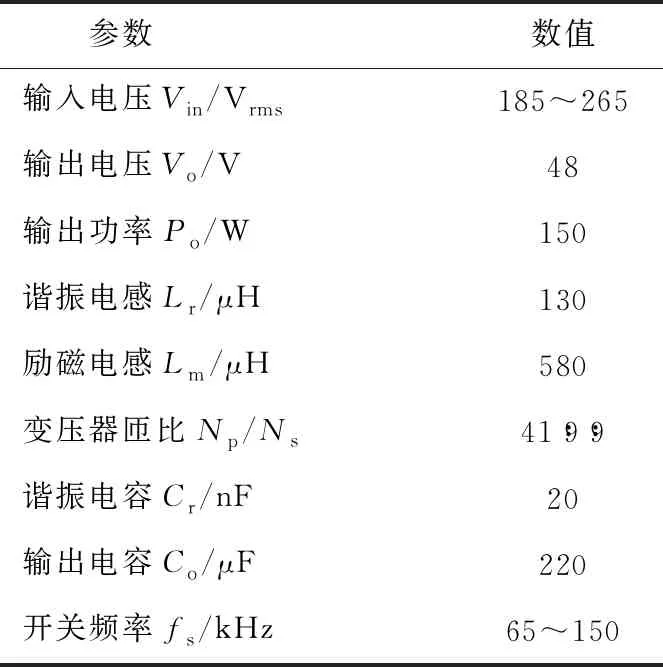
4.1 输入特性与母线电压
4.2 开关管软开关特性

5 实验结果与分析

5.1 输入特性和母线电压




5.2 谐振电流波形

5.3 开关管软开关特性


5.4 副边整流二极管电压、电流波形

6 结 论

