一种抑制开关磁阻电机转矩脉动的电流控制方法

孟繁贵， 张文鹏， 刘爱民， 王宇琛， 张红奎,3

(1.沈阳工业大学 电气工程学院，辽宁 沈阳 110870； 2.沈阳工业大学 机械工程学院，辽宁 沈阳 110870；3.中煤科工集团沈阳研究院有限公司，辽宁 沈阳 110066)

0 引 言

开关磁阻电机(switched reluctance motor,SRM)具有简单的转子结构、较大的启动转矩、优越的调速性能以及低廉的制作成本等优点，在电动汽车行业拥有广阔的应用前景。但它的双凸极结构、强非线性和步进式旋转导致其转矩脉动很大，阻碍其在汽车工业的发展[1-3]。因此研究SRM转矩脉动的抑制方法具有重要的科研意义和经济价值。

常用的抑制SRM转矩脉动的控制方法主要有直接转矩控制[4-6]、直接瞬时转矩控制[7-9]、转矩分配函数控制[10-12]和谐波注入法[13-14]。直接转矩控制和直接瞬时转矩控制需要实时反馈输出转矩，增加了系统的复杂性，影响系统的控制精确度。转矩分配函数控制方法根据转子位置与开通、关断角的关系，按照制定的转矩分配函数分解参考转矩或参考电流，该方法不仅需要选取恰当的分配函数，而且开通、关断角的选定也会影响SRM的转矩控制效果。谐波注入法通过向参考电流中额外注入多次谐波分量以补偿或抵消输出转矩，损失了部分系统效率。通过对以上方法进行分析，发现常用的SRM转矩脉动抑制控制方法离不开转矩反馈、转矩分配函数的制定以及开通、关断角的调节模块，或是对系统效率有所影响。

本文提出的电流控制方法参考转矩脉动较小的同步电机控制。同步电机的转矩是由两个正弦分布、转速和方向一致的旋转磁场相互作用产生。本文借鉴同步电机的dq轴控制思想，将转速控制器输出值经坐标变换得到三相参考电流函数。由于SRM的电流始终为正且电感关于转子位置的函数为扭曲的正弦信号，两者与同步电机的正弦信号有较大差异，因此三相参考电流函数还需经过非负处理和修正后，才可转化成最终的三相参考电流用于电流滞环控制。此外加入电流前移模块，采用模糊算法调整移动角，避免转速较高时关断相续流对系统效率的影响。提出的电流控制方法免去了常规转矩脉动抑制方法中的转矩反馈以及转矩分配函数、开通和关断角的选定环节，降低控制系统复杂性的同时保证了转矩的平稳和系统效率。本文在三相9/6极SRM平台进行传统电流控制和提出的电流控制方法的仿真和实验测试，结果证明提出的电流控制方法可有效降低SRM转矩脉动且具有较高可行性。

1 电流控制方法

本文提出的电流控制系统如图1所示，在传统电流控制基础上加入电流前移、坐标变换、非负处理和电流修正四个模块。整个控制系统没有转矩、磁链实时反馈模块，无需设置开通、关断角，与SRM转矩控制系统相比操作简单，易于实现。

图1 提出的电流控制系统示意图

1.1 坐标变换

根据交流电机的坐标变换原理[15]，在保证功率守恒的情况下，三相9/6极SRM的参考电流函数表示为

(1)

式中：fix(x=a,b,c,d,q)为与转子位置相关的电流函数；θe为SRM的电角度。图2是fiq=1.225且fid=0时坐标变换后的参考电流函数曲线。

图2 坐标变换后的参考电流函数曲线

1.2 非负处理

参考同步电机的转矩公式，SRM的转矩公式可以表示为

T=fiafθa+fibfθb+ficfθc。

(2)

式中fθx(x=a,b,c)为与转子位置相关的函数。理想情况下，如果fθx为标准的正弦函数，fix是与fθx同相位的正弦函数，那么SRM将输出恒定的转矩T。

理想的fix和fθx应表示为：

(3)

(4)

与同步电机不同的是SRM的电流始终为正，因此，在保证转矩守恒前提下SRM的一相或两相负电流所承担的转矩需要分配给其他相电流。当a相电流为正，b相和c相电流为负时，a相关于b相和c相负电流应增加的电流函数分别表示为：

(5)

(6)

在此情况下非负处理后三相参考电流表示为

(7)

当a相电流为负，b相和c相电流为正时，b相和c相需分担的转矩分别为：

(8)

(9)

根据式(8)、式(9)和式(2)～式(4)可得

(10)

(11)

此时非负处理后三相参考电流为

(12)

若仅有b相或c相电流为正或为负时，电流的非负处理方法与a相电流的处理方法相同，在此不做赘述。因此在保证转矩恒定的情况下，非负处理后的SRM参考电流函数曲线如图3所示。

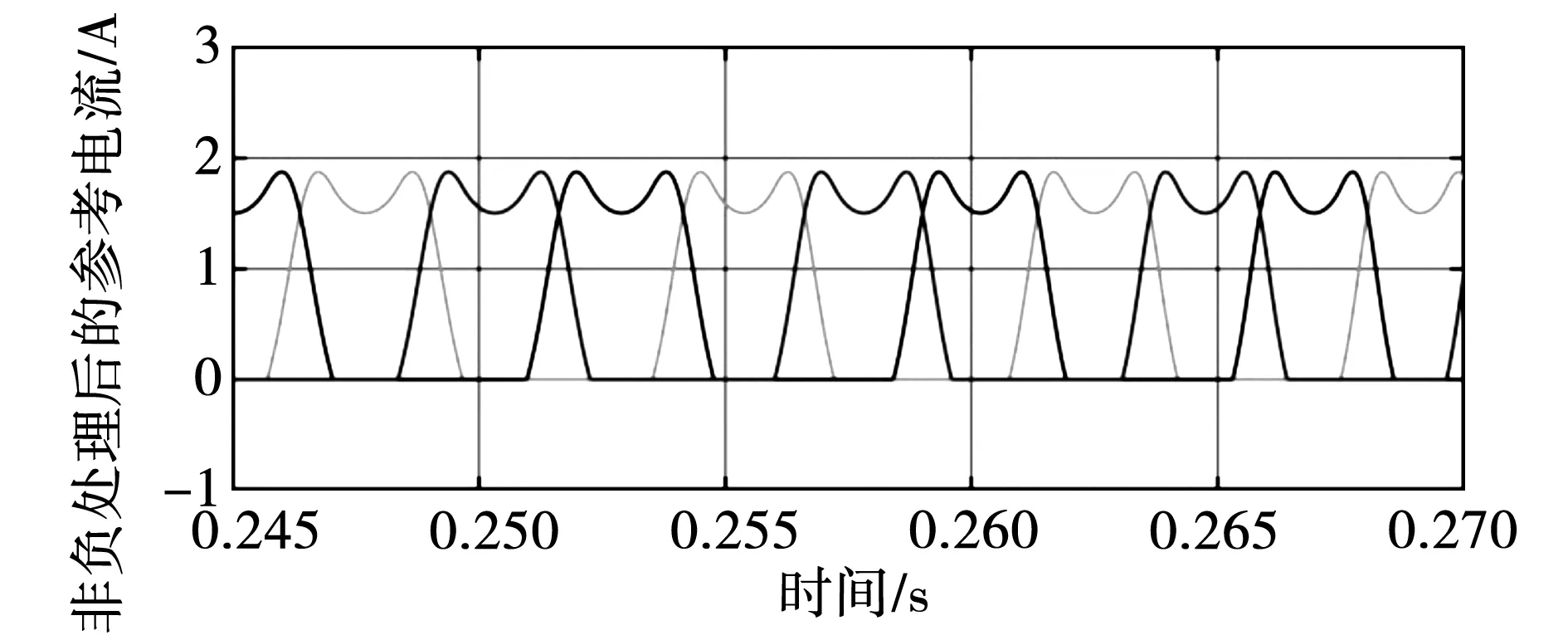
图3 非负处理后的参考电流函数曲线

1.3 电流修正

通过非负处理后，在保证输出转矩不变的前提下，SRM的参考电流函数fix满足与fθx同相位且为正弦函数的要求。若要输出恒定的转矩，还需保证与转子位置相关的函数fθx为标准的正弦信号。而SRM的fθx函数曲线与图4(a)所示的SRM静态转矩特性曲线变化趋势一致，是“扭曲”的正弦函数，因此需要对特定电流的T-i-θ曲线归一化处理后与sinθe相除，得到补偿系数H(θ)。图4(b)为补偿系数倒数的曲线，从图中可以看出，SRM转子位置角度在0°～8°时，1/H(θ)随着电流变化显著。转子位置角度在8°～20°时，1/H(θ)几乎不变。当角度处于20°～30°区间时，1/H(θ)的值介于0°～1之间，受电流影响较小。30°～60°的1/H(θ)与0°～30°的1/H(θ)对称分布，因此，1/H(θ)仅在0°～8°和52°～60°受电流影响较大。

图4 相关函数曲线

本文的SRM定、转子极弧分别为21°和22°，图5为转子位置角度示意图。8.5°时定、转子齿部刚刚接触，在此之前电感变化率几乎为零，因此在0°～8°和52°～60°期间参考电流的变化对输出转矩的影响很小。在不影响转矩控制效果的前提下，为了降低控制系统的复杂性，补偿系数可以看作仅与转子位置相关。将非负处理后的参考电流与1/H(θ)相乘后，得到修正后的参考相电流，即Ia_ref、Ib_ref和Ic_ref。

图5 转子位置角度示意图

1.4 电流前移

低速状态下，转速PI调节器的输出值在经过坐标变换、非负处理和电流修正后得到三相参考电流Ia_ref、Ib_ref和Ic_ref，实际电流若能实时跟踪参考电流，输出转矩将保持恒定。事实上由于本文SRM的功率变换器采用不对称半桥电路，各相绕组在换相结束时伴有续流现象，SRM的电流跟踪效果并不理想。根据SRM的电动势平衡方程式

(13)

式中，uk，ik，Rk和Lk分别为SRM第k相的端电压、电流、电阻和电感。经变换

(14)

式中Ω为SRM的角速度。由式(14)可知，随着角速度的增加，绕组的电流变化率会下降，换相时关断相的续流时间会延长，未及时关断的电流会在电感下降区产生负转矩，损失部分系统效率。

为了避免由转速升高导致的系统效率的损失，在不影响转矩脉动抑制效果的前提下，本文通过调节fid将参考电流的关断提前，以减少负转矩的产生。电流前移的原理示意图如图6所示，在保证转速控制器输出总量不变的前提下，dq轴的控制信号可表示为

图6 电流前移的原理示意图

(15)

式中θdq为移动角。图7为SRM工作状态不变时不同θdq对应的参考电流曲线。

图7 不同θdq对应的参考电流曲线

如图7所示，当fid为正时，随着θdq的增加，参考电流的峰值逐渐变小，电流曲线整体发生后移，关断相电流在电感下降区产生负转矩的几率变大。fid为负时，参考电流的变化趋势与fid为正时完全相反，降低了负转矩产生的可能性，满足电流前移的要求。因此修改后的dq轴控制信号为

(16)

从图7(b)中观察到，θdq的增大对参考电流曲线前移的影响逐渐变小，而过度的电流前移会导致绕组在电感变化率很小时导通，消耗的电流几乎不产生转矩。因此根据SRM的转速，恰当地选择移动角对保证系统效率和转矩平稳尤为重要。

移动角和电机转速两者间没有明确的函数关系，因此本文采用模糊算法调节移动角。随着转速的增加，SRM关断相电流的续流效应越发明显。表1为不同转速下SRM的相电流关断角，此处相电流关断角为关断相电流下降为零时转子的机械角度。如表1所示，转速大于500 r/min时，SRM的续流效应即可产生负转矩，因此在转速高于500 r/min后，提出的电流控制系统加入电流前移模块。

表1 不同转速下SRM的相电流关断角

本文采用二维模糊调节器，输入变量为实际转速与500 r/min的差值e和差值的变化率ec，输出变量为移动角u。将输入变量模糊化：

(17)

式中k为比例因子，选取合适的比例因子可将模糊后的变量恰好落到模糊论域中。根据变量的实际情况将E和u的模糊论域及模糊语言变量定为[0,6]和正小(PS)、正中(PM)、正大(PB)，EC的模糊论域及模糊语言变量定义为[-6,6]和负大(NB)、负中(NM)、负小(NS)、正小(PS)、正中(PM)、正大(PB)。移动角的调节应遵循以下规律：

1)当实际转速小于500 r/min时，移动角为零。

2)当实际转速大于500 r/min时，应当增加移动角。当实际转速过高时，移动角应大幅度增加。

根据移动角的调节规律，输入、输出变化量的隶属度函数和模糊规则如图8和表2所示。模糊控制器的输出变量u采用加权平均法解模糊，如式(18)所示，即可得到电流前移模块的移动角。

图8 输入、输出变化量的隶属度函数

表2 模糊规则

(18)

式中：vi为论域元素,即隶属度函数的横坐标值；μu为隶属度函数。

2 仿真结果及分析

本文在7.5 kW SRM的控制系统上进行传统的电流控制和提出的电流控制仿真，电机运行速度分别为500、1 000 r/min，负载为10 N·m。SRM的电流和转矩仿真结果如图9和图10所示，图11为两个转速和电流控制方法下的SRM转矩脉动。

如图所示，SRM在传统电流控制时，三相电流较平稳，而输出转矩在电机换相期间的脉动很大，这是因为传统电流控制仅起到电流斩波的效果，控制时并未考虑转矩的稳定。而提出的电流控制方法是以转矩守恒为前提，对三相电流进行闭环控制，因此该方法下的输出转矩在单相绕组通电或换相时都能基本保持稳定，如图9(b)和图10(b)所示。

图9 500 r/min时SRM的电流和转矩仿真曲线

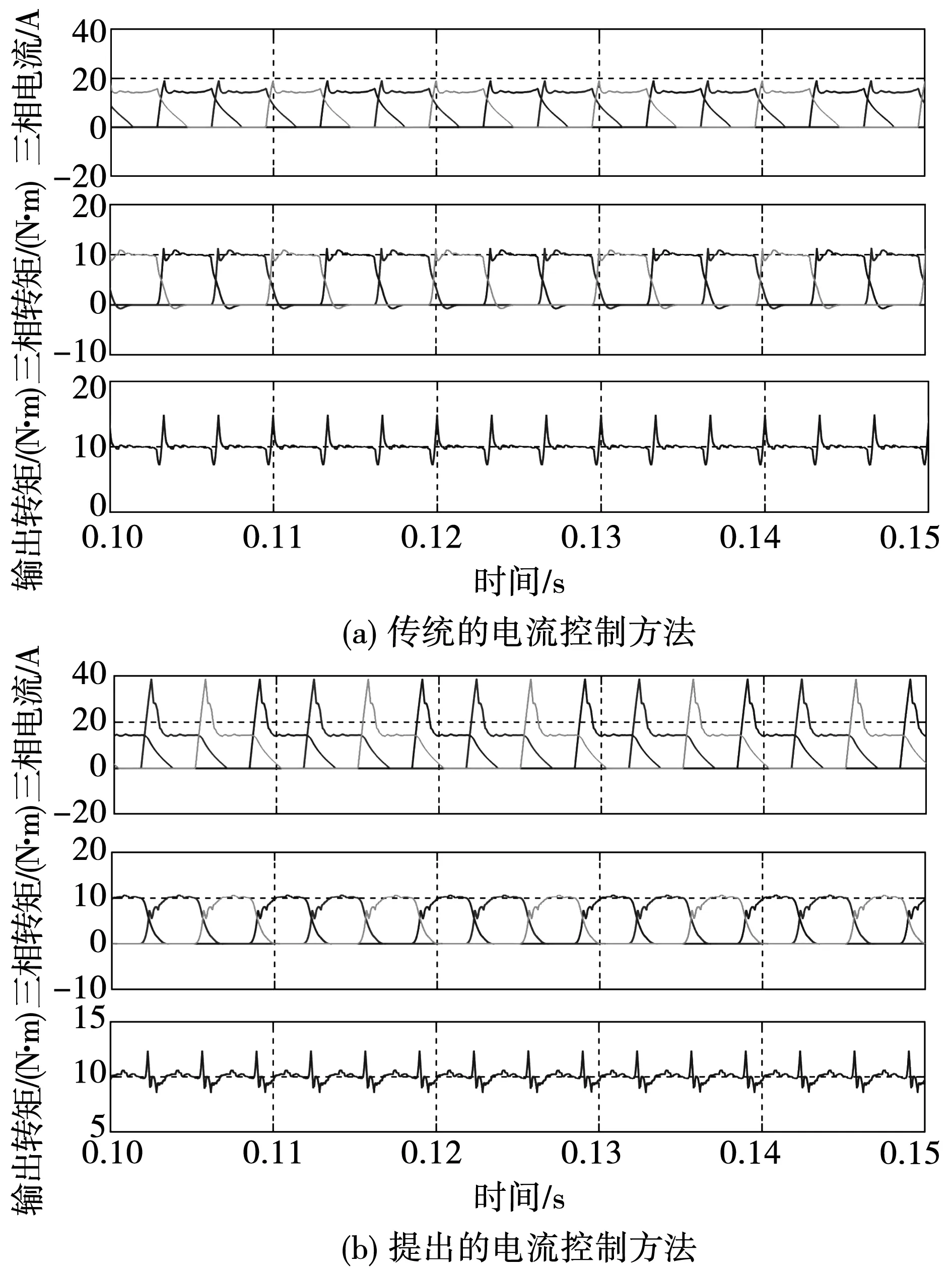
图10 1 000 r/min时SRM的电流和转矩仿真曲线

图10(a)中SRM三相转矩有明显的负转矩，这是由于电机转速提高引起的。根据式(14)可知，转速越高，电流变化越慢，未及时降至零的关断相电流在电感下降区产生负转矩，不仅增加了转矩脉动，还损失了部分系统效率。从图10(b)和图11中可知SRM三相转矩无负转矩，转矩脉动比500 r/min时传统电流控制方法还低，可见提出的电流控制方法可以在保持系统效率的前提下起到降低转矩脉动的作用。

图11 两个转速和电流控制方法下的SRM转矩脉动

3 实验结果及分析

7.5 kW SRM的控制系统实验平台如图12所示，该平台采用DSP TMS320F28335作为核心控制器，功率变换器采用不对称半桥电路，负载由直流电源供电，涡流测功机提供可调阻力。在该平台上测试不同转速下的两种电流控制方法，进一步验证提出的电流控制方法的有效性和可行性。

图12 7.5 kW SRM的控制系统实验平台

图13和图14分别为500 r/min和1 000 r/min时SRM的电流和转矩实验曲线，图片上方为输出转矩曲线，下方为三相电流曲线，可以看出实验曲线与仿真的转矩、电流变化趋势基本相同。图15为不同转速和电流控制方法下的转矩脉动。由图可知，SRM以不同转速运行时，提出的电流控制方法与传统电流控制相比，转矩脉动均大幅度降低。此外，受仿真的建模精度和实验的测量误差影响，实验的转矩脉动较高于仿真。

图13 500 r/min时SRM的电流和转矩实验曲线

图14 1 000 r/min时SRM的电流和转矩实验曲线

图15 不同转速和电流控制方法下的转矩脉动

4 结 论

本文提出了一种抑制SRM转矩脉动的电流控制方法。通过不同转速下SRM控制系统的仿真和实验证明，与传统电流控制相比，该方法可以在不损失系统效率的前提下有效降低转矩脉动。与常用的SRM转矩脉动抑制控制方法相比，省去了转矩的实时反馈以及转矩分配函数、开通和关断角的调节模块，为抑制SRM的转矩脉动提供了一种简单有效、方便可行的控制方法。