误差自校正随机脉冲宽度调制相电流重构研究

申永鹏， 刘迪， 王延峰， 李海林， 孟步敏

(1.郑州轻工业大学 电气信息工程学院，河南 郑州 450000；2.湘潭大学 自动化与电子信息学院，湖南 长沙 410000)

0 引 言

三相交流电机广泛应用于高精度的伺服控制系统、电动汽车等领域，电压空间矢量脉宽调制技术(space vector pulse width modulation, SVPWM)也随之应用于三相交流电机驱动系统。矢量控制的核心是电流控制，电机相电流是矢量控制系统和保护策略的关键参数，相电流的准确检测对提高电机控制系统性能具有重要意义[1-7]。单电流传感器通过对直流母线或特定桥臂瞬时电流的分时刻采集，并将其映射至不同的相电流，具有成本低、精度高、可以消除多个电流传感器之间不一致性等优点[8-9]，同时实现对零点漂移的检测和校正，以提升电流检测精度，是电驱动控制领域的研究热点。

但是，传统SVPWM采样时间窗口过短，无法进行可靠的相电流采样，如何设计新的脉宽调制策略方法极其重要。制约单电流传感器相电流重构检测精度的因素为：1) 在不可观测区域有效电压矢量作用时间过短，而无法可靠进行相电流采样；2) 由于电流传感器及信号处理电路产生的漂移。

针对在不可观测区域内相电流重构方法，文献[10]提出插入测量矢量的相电流重构法以解决有效电压矢量持续时间过短的问题。文献[11]提出预测状态观测器重构电流的方法。文献[12]提出在固定点预测采样电流的相电流重构法。为了减少电流失真和扩大电流重构范围，通过脉宽调制(pulse width modulation, PWM)技术进行优化。文献[13]提出不使用零开关状态的PWM与空间矢量调制结合的新方法，扩大了相电流重构的范围。文献[14]通过采用互补的有效矢量代替零矢量，优化了控制过程，减少了控制误差。文献[15]直接采用基于叠加原理的相电流重构方法，克服了传统PWM方法的不足。文献[16]定义新的参考电压通过三个相邻开关状态合成，称为三态脉冲宽度调制。为获得不可观测区域内的电流信息，使用多位置耦合的拓扑结构进行相电流重构。文献[17]耦合了A相桥臂和B相输出电流相，完成不可观测区域的相电流重构。文献[18]耦合A相B相之间上桥臂和B相C相下桥臂的位置，使得不可观测区域的相电流得以重构，把低调制区移向了空间矢量六边形边界。上述两种耦合方式提高了不可观测区域的电流检测窗口的时间，但其缺点为在使用零矢量作用时段内进行电流采样的同时也会造成正常区域内有效矢量无法测量。文献[19]提出多支路耦合方式，可同时完成有效矢量和零矢量作用时段内的电流检测，消除不可观测区域。

上述方法仅仅消除或者缩小了电流不可观测区域，未考虑电流传感器零点漂移对电流测量精度带来的影响。针对上述问题，本文提出一种误差自校正随机脉冲宽度调制方法(error calibration and random SVPWM,ECR-SVPWM)，通过定义最小采样时间，精确划分出母线电流采样不可观测区域。对于不可观测区域，通过随机数发生器对载波进行相应的移位，延长非零开关状态的持续时间，获得新的观测窗口，实现传统SVPWM不可观测区域内相电流的重构，同时对互补有效矢量动态电流双采样，实现电流零点漂移量的自检测和自校正，提高电流重构精度。

1 误差自校正随机脉冲宽度调制策略

1.1 直流母线采样原理

在实际直流母线电流采样系统中，必须考虑开关器件的实际特性、电流波动和数模转换器A/D的工作时间。直流母线电流稳定过程如图1所示，定义最小可靠电流采样时间[20-22]为

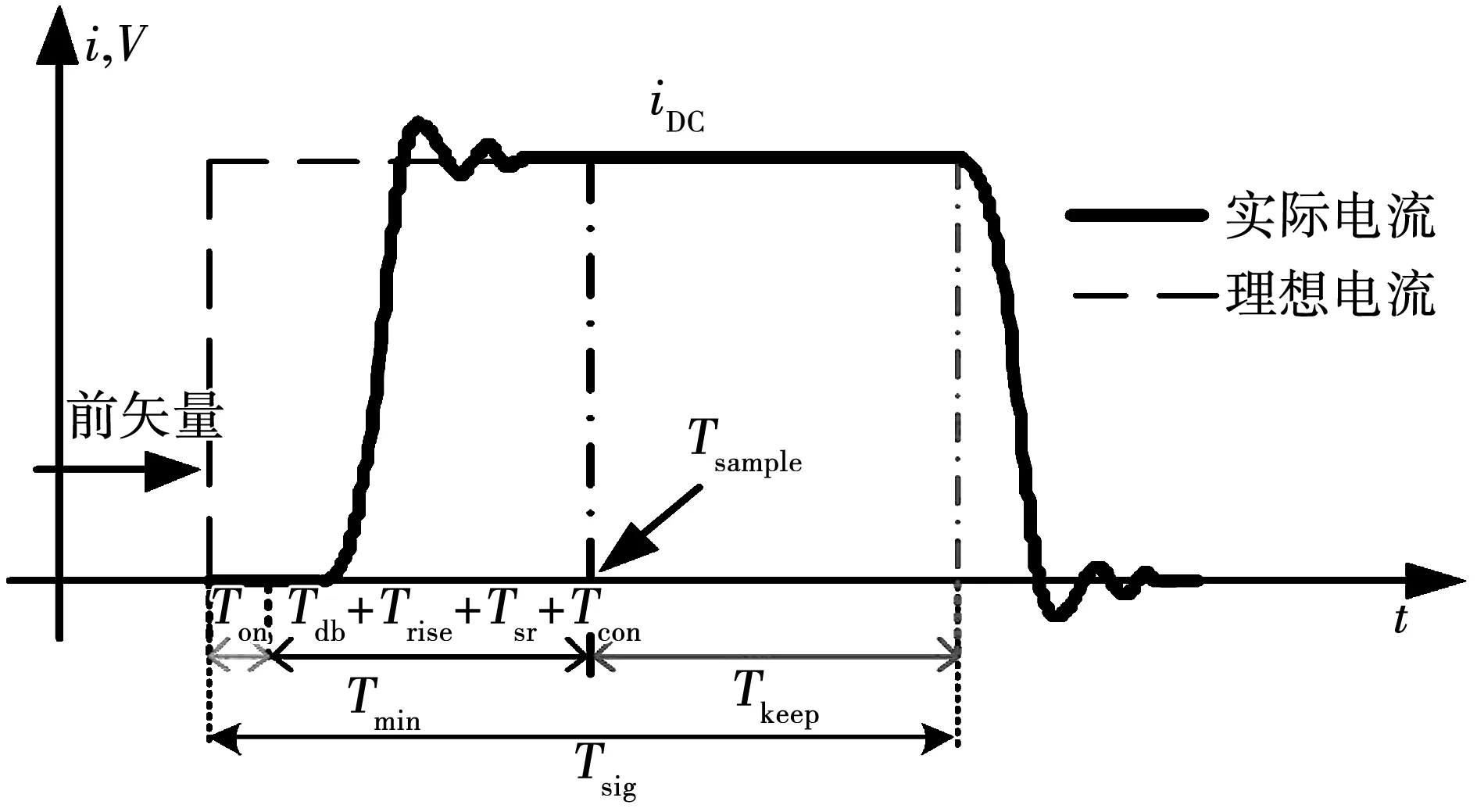
图1 直流母线电流稳定过程

Tmin=Ton+Tdb+Trise+Tsr+Tcon。

(1)

式中：Ton为IGBT的导通延迟时间；Tdb为三相逆变电路的死区时间；Trise为导通后电流上升时间；Tsr为电流稳定时间；Tcon为数模转换器A/D的工作时间。

三相两电平电压源型逆变系统拓扑结构如图2所示。根据电压空间矢量脉冲宽度调制的基本原理，可知一共有8种开关状态，6个有效电压矢量和2个零电压矢量[23-25]，[V1(100)，V4(011)]、[V2(110)，V5(001)]、[V3(010)，V6(101)]为三组互补的矢量。其中矢量作用时，定义系数Ni(i=1, 2, 3)，Ni=1表示上桥臂开关闭合，Ni=0表示下桥臂开关闭合。根据开关状态可以得到相电流ia、ib、ic分别与直流母线电流idc的关系为：

图2 直流母线采样的电压源型逆变电路

idc=N1ia+N2ib+N3ic；

(2)

ia+ib+ic=0。

(3)

结合式(2)和式(3)可以获得直流母线电流与三相电流(ia、ib、ic)的关系，如表1所示。

表1 电压矢量与相电流的对应关系

由于一个周期Ts内的前半周期PWM(Ts/2)和后半周期PWM(Ts/2)是对称的，把前半个周期作为分析对象。两个相邻有效电压矢量V1(100)和V2(110)的作用时间分别为Tsig1和Tsig2，如图3所示。在有效矢量作用时间段内分别对其进行两次采样得到相电流ia和-ic，但由于考虑最小可靠电流采样时间Tmin的影响，如图3中灰色阴影部分所示，而Tmin的影响在扇区边界更加明显。

图3 电流检测窗口

参考电压矢量v*可表示为

(4)

各矢量作用时间以占空比形式表达为：

(5)

当v*处于扇区边界时，如图4(b)所示，有效矢量V2(110)(箭头所示)作用时间d2V2小于Tmin(阴影部分所示)，将导致电流无法采样。如果参考电压矢量进入低调制区，两个采样窗口都将消失，因此定义式(4)，当出现式(4)的情况时，三相PWM占空比接近，开关状态维持时间太短，无法进行可靠的电流采样。由最小电流采样时间定义的不可观测区域的扇区边界和低调制区域如图4(a)所示。

图4 电流不可观测区域

1.2 ECR-SVPWM调制原理

当电压空间矢量进入电流不可观测区域时，ECR-SVPWM通过随机数发生器来调整相应相的输出脉宽位置，进而提供新的电流观测窗口。令ti(i=1,2,3)来表示PWMn(n=1,2,3)的上升沿时间。由图3可知，若PWM1和PWM2的占空比接近，ψ=1，有效电压矢量V1(100)的作用时间小于Tmin，此时只能获得一相电流信息-ic。ECR-SVPWM通过将PWM1信号随机移位，进而产生可靠的测量窗口。同理，其他PWM移相规则如表2所示。

表2 PWM信号移相规则

图5(a)为存在正常电流检测窗口的三路PWM波形；图5(b)为出现电流检测窗口小于最小采样时间Tmin的三路PWM波形；图5(c)和图5(d)为使用随机脉宽调制策略后出现可靠电流检测窗口的三路PWM波形。

图5 ECR-SVPWM调制原理

SVPWM的载波函数和ECR-SVPWM的载波函数分别为：

(6)

(7)

式中：ε(x)为阶跃函数；A为载波峰值；E为常数1；Ts为载波周期。此外，为确保脉冲宽度信号的完整性，将随机数ran()限制在0～1之间，再将随机数乘以随机数的取值范围，即

R1former=ran(0,1)2A(1-C)。

(8)

式中：C为脉宽调制的占空比；R1former为脉宽调制信号发生相移的实际上升沿位置，有：

(9)

式中ta和tb分别为移相后脉宽调制信号的上升时间和下降时间。

当ψ值不同时，PWMn(n=1, 2, 3)信号的上升时间Ta、Tb和Tc被赋不同的值，表达式为

(10)

式中ti(i=1,2,3)为原始空间矢量脉宽调制波形的上升时间。

定义参考电压Vref，在传统的SVPWM周期中，参考电压矢量表示为

VrefTs=V1T1+V2T2+V0T0+V7T7。

(11)

式中：T1为V1(100)的作用时间；T2为V2(110)的作用时间；T0和T7为两个零电压空间矢量的作用时间。

(12)

(13)

移相前后参考电压如图6所示，通过V1和V2可以构建出V3， 即

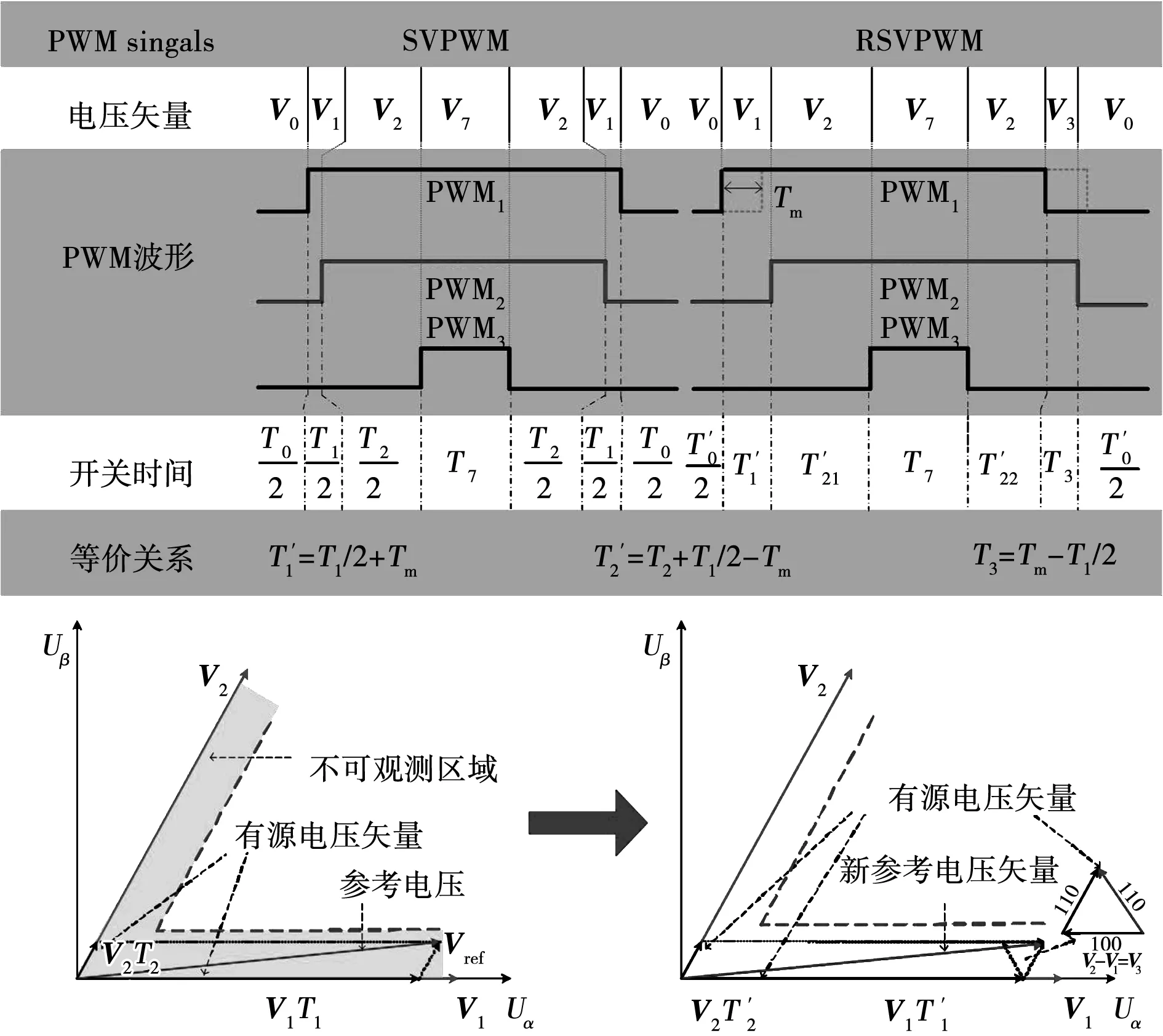
图6 移相前后参考电压

V3=V2-V1，

(14)

故有

(15)

验证了移相后的参考电压矢量与传统SVPWM的参考电压矢量完全一致。

1.3 电流采样

使用SVPWM(ψ=0)和ECR-SVPWM(ψ≠0，ψ=1,2,3)相结合的相电流采样方法如图7所示。

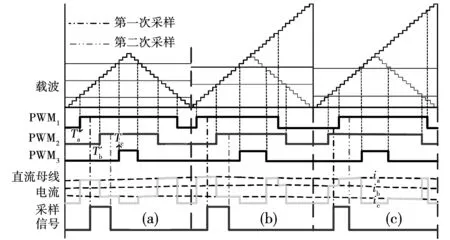
图7 采样时刻和直流母线电流

传统的SVPWM一个调制周期内采样两次。由图7(a)可知，第一次采样时间是Tsample1=(Ta+Tb)/2+Tdelay，第二次采样时间Tsample2=(Tb+Tc)/2+Tdelay，其中采样延迟为

Tdelay=Trise+Tsr。

(16)

另外，在传统SVPWM中可观测区域的两次采样时间满足：

Tsample1=

(17)

Tsample2=

(18)

式中N为扇区号。

三个脉冲宽度信号的上升时间分别分配给R、M和W，表达式为

(19)

相移后，不同的相位关系分别由x、y和z的值表示。R>M→x(真：x=1；假x=0)，M>W→y(真：y=1；假：y=0),R>W→z(真：z=1；假z=0)。

由图7(b)和图7(c)可知，在不可观测区中第一采样时间和第二采样时间为：

(20)

(21)

1.4 相电流重构原理

图8给出了ψ=1时移相的所有情况。可以看出，在不同的H值下，两个采样到的电流信息是不同的。ψ值不同，同样会导致采样电流信息的不同。

图8 采样电流

综上所述，采样值与相电流之间的关系由“ψ”值和“H”值决定。

在提出的相电流重构方法中，设置电流偏移来区分电流极性，通过数模转换器的采样输出包括偏移分量Soffset。如果将两个采样输出分别视为S1th和S2th，则实际采样值va和vc计算为va=S1th-Soffset和vb=S2th-Soffset，ia、ib、ic值为：

(22)

式中G是直流母线电流检测单元的增益。

1.5 电流零点漂移校正原理

在实际的电机控制系统中进行相电流采样时，直流母线电流带来的零点漂移是造成重构误差的主要原因，因此校正电流零点漂移对于提高电流重构精度和交流电驱动闭环控制系统稳定性至关重要。

直流母线电流零点漂移原因主要包括：1)电压基准芯片的输出精度和稳定性受初始精度、温度、噪声等影响造成漂移量；2)霍尔传感器内部霍尔元件和运算放大器受温度影响直接造成霍尔电流传感器输出信号的零点漂移；3) 放大器内部参数不一致和起主导作用的温度变化等因素导致的零点漂移。

由表2可知，当两个互补矢量作用时，所对应的直流母线电流大小相等，方向相反。在ECR-SVPWM方法中，一个载波周期内，在不插入新的测量矢量时构造出互补矢量，对其采样得到采样电流I1和I2。假设实际电流值为It，零点漂移导致的漂移量为Is， 则有：

(23)

实际电路中，由于零点漂移的存在Is≠0，有

I1+I2=2Is。

(24)

由此可以计算出漂移量Is，从而得到校正后的电流为：

(25)

从而实现了相电流零点漂移的校正。

2 实验验证

为了验证ECR-SVPWM技术的有效性，搭建实验平台如图9所示。采用TMS320F28035型数字信号器，PWM载波频率为10 kHz，三相感应电机MODVK48T17D200K作为控制系统的驱动电机。实验结果的采集和分析由电驱动分析仪MDA508A来完成。负载相电流波形用A150电流探头检测，实验所用电机具体参数如表3所示。

图9 实验装置

表3 三相感应电动机参数

在实验中，脉宽调制的死区时间为2 μs，最小采样时间Tmin=5 μs。ECR-SVPWM波形及对应采样时刻如图10所示，图10(a)为正常区域，在出现不可观测区域后进行随机移相，移相结果如图10(b)和图10(c)所示，图10(d)为第三次采样用于校正电流信息，图10(e)～图10(h)为采样电流信息。

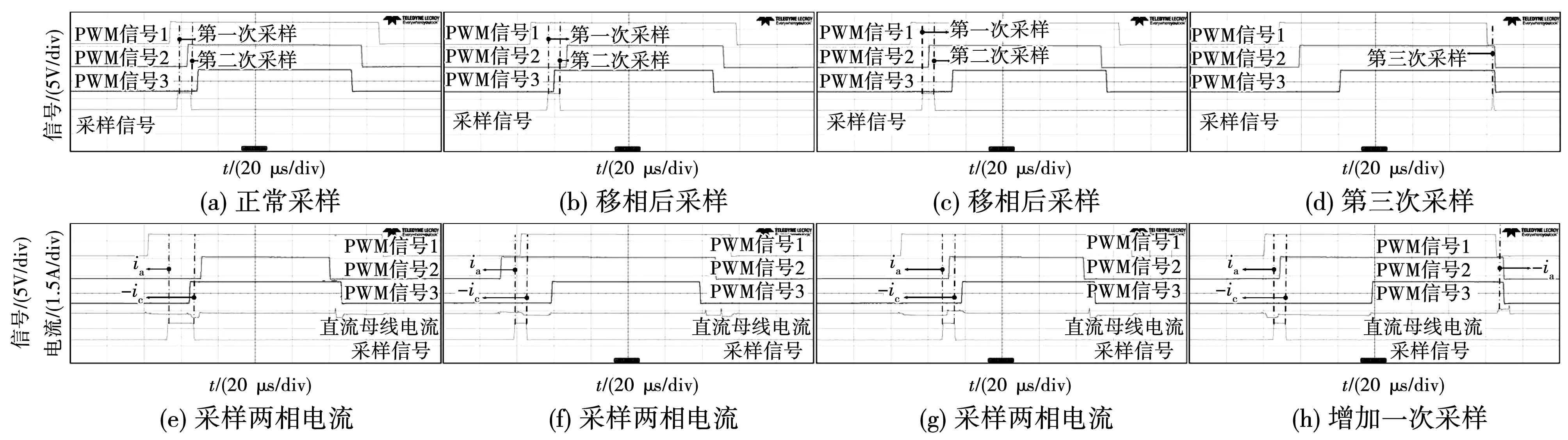
图10 ECR-SVPWM波形及对应采样时刻

传统中心对称七段式SVPWM如图11(a)所示，Ts为载波周期，阴影部分表示有效电压矢量作用时间。传统中心对称七段式SVPWM时，开关顺序为000→100→110→111→110→100→000，且两侧电压矢量的作用时间呈现对称模式，因此一个载波周期中的开关次数为6，如图11(a)中六个圆圈所示。ECR-SVPWM由于使用了单增计数的载波方式以构造随机移相策略，使得电压矢量呈现不对称模式，但保持占空比不变，开关状态仍为000→100→110→111→110→100→000，如图11(b)双箭头所示。其开关状态切换的时间点被改变，仍保持一个周期内6次的开关次数。因此，所提出的ECR-SVPWM可以在相同的载波频率下与传统的SVPWM开关损耗保持一致。

图11 三相开关状态示意图

ECR-SVPWM策略对于电流零点漂移的校正效果如图12所示，校正未使能时，交流输出侧电流钳所测的结果稳定为0，由于漂移现象导致了所测直流母线电流结果不为0，呈现上下波动状态。

图12 零点漂移校正分析

ECR-SVPWM策略使能校正后，电流漂移量大幅下降，对数据分析得到如图12(b)所示的波形，电流零点漂移降低65%。电机启动过程如图13所示，在电机启动前使能电流零点漂移校正，校正效果明显。

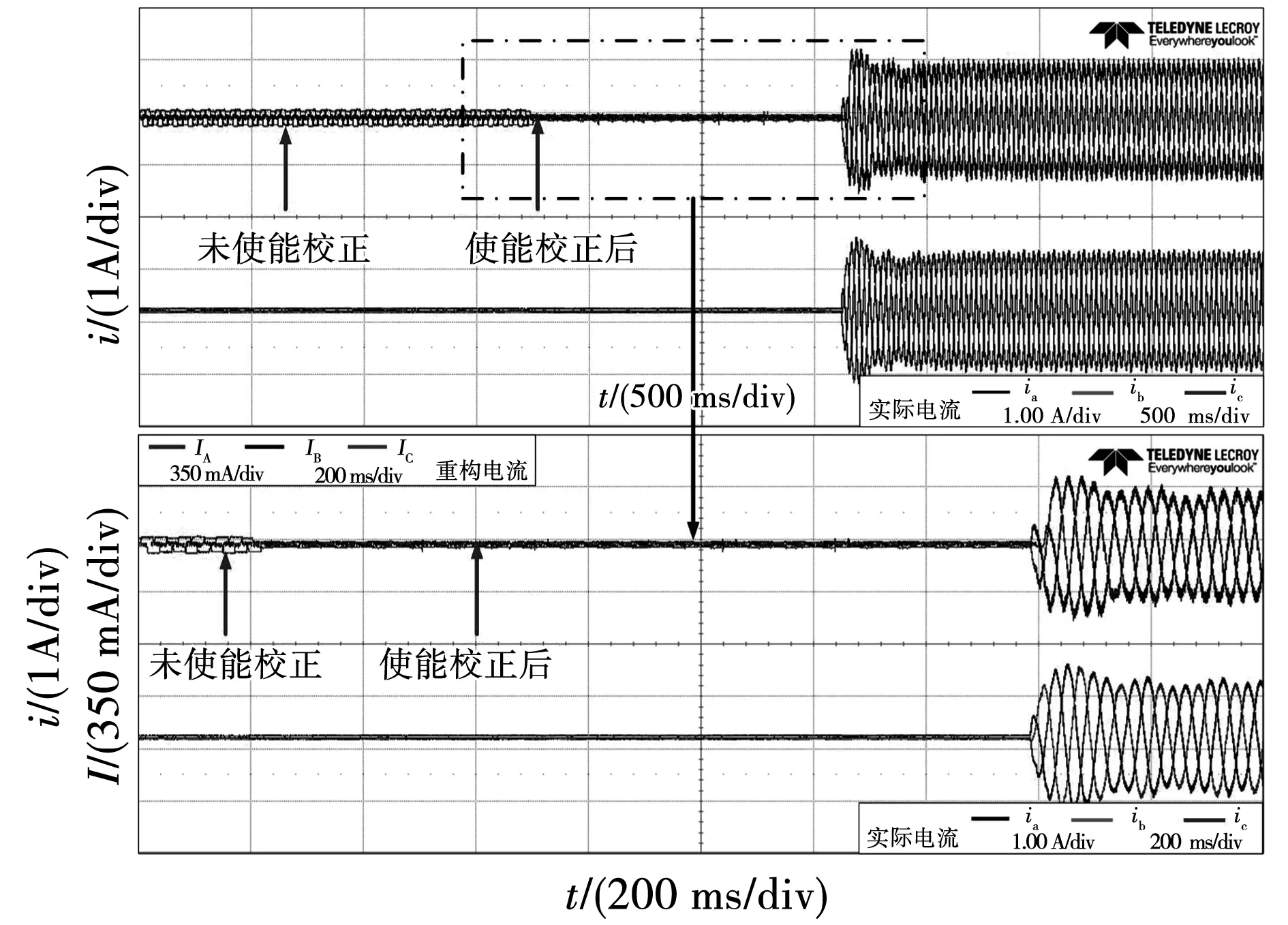
图13 ECR-SVPWM电机启动时刻零点漂移校正

在低调制度下，重构和实测相电流如图14所示。由于两次采样时刻不同步和重构算法执行时间等因素，比实测相电流有滞后现象。校正前后A相实测和重构曲线如图15和图16所示。校正后重构误差由原来的3.5%降低为3.1%。在整个矢量平面内，电流能够平稳过渡且在不可观测区域内，并精确重构相电流。

图14 低调制度ECR-SVPWM重构和实测相电流

图15 校正前ECR-SVPWM重构和实测相电流

图16 校正后ECR-SVPWM重构和实测相电流

为测试ECR-SVPWM策略校正前后对电流波形的优化效果，将调制度增加到0.7，捕捉到校正前电流开始出现畸变，如图17所示。但校正策略的加入使得重构电流曲线更加圆滑，重构误差控制在3.1%以内，如图18所示，验证了ECR-SVPWM策略在相电流重构过程中的可靠性和稳定性。

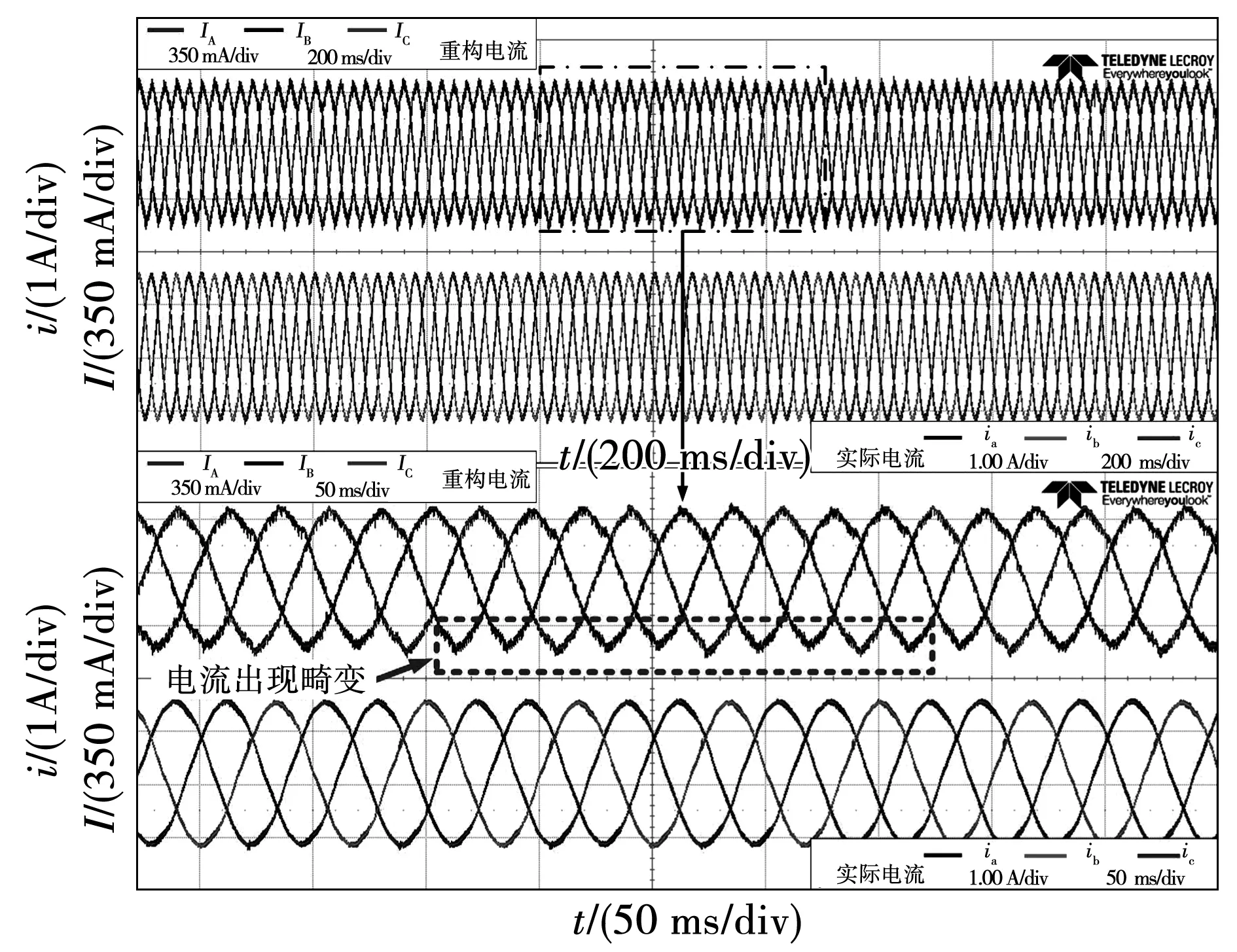
图17 调制度0.7校正前ECR-SVPWM重构和实测相电流

图18 调制度0.7校正后ECR-SVPWM重构和实测相电流

为了验证ECR-SVPWM策略的电流闭环控制效果，开展了iq突变和稳态下的电流重构效果验证。图19为iq突变条件下ECR-SVPWM重构和实测相电流，可见，在电流动态调整过程中，重构电流与实测电流一致。图20为闭环稳态条件下ECR-SVPWM重构和实测相电流。

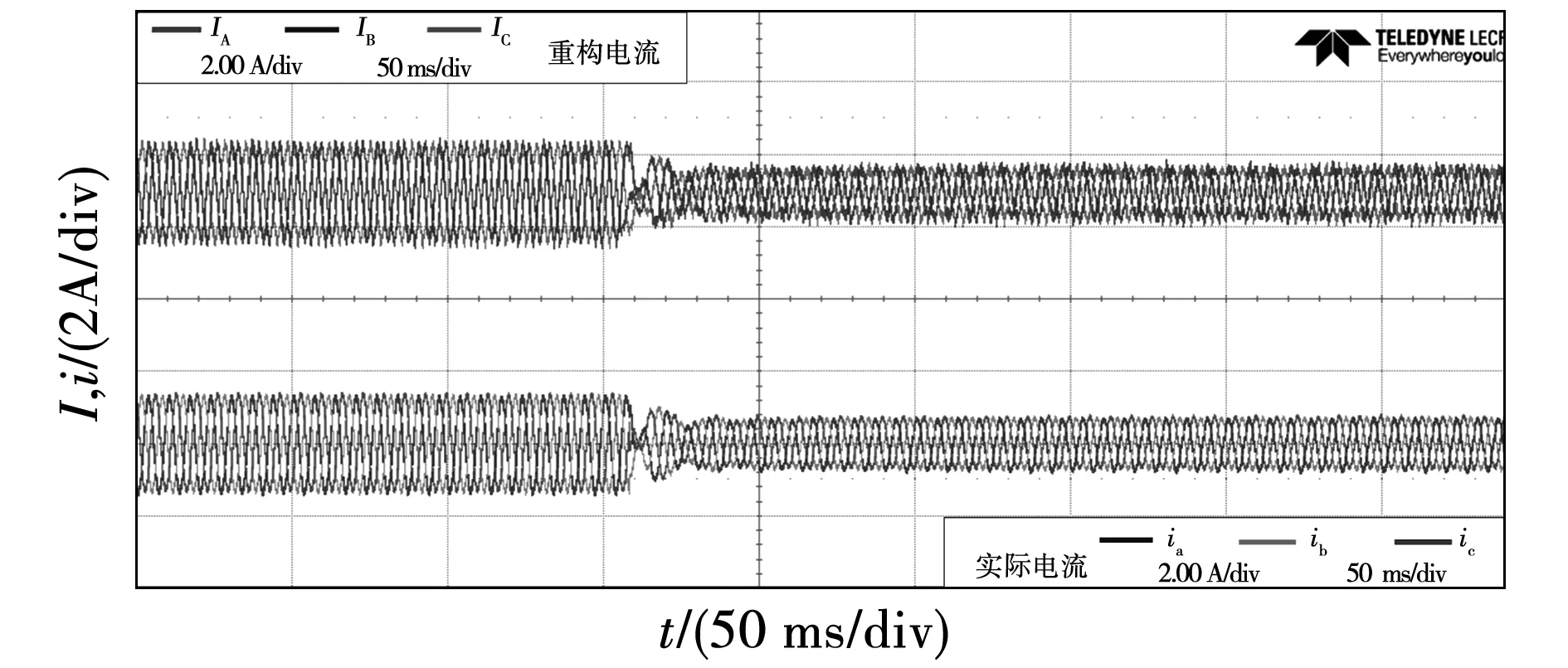
图19 iq突变条件下ECR-SVPWM重构和实测相电流

图20 闭环稳态条件下ECR-SVPWM重构和实测相电流

对SVPWM和ECR-SVPWM两种方法实测相电流波形进行快速傅里叶变换(fast Fourier transform,FFT)分析，如图21所示。由于ECR-SVPWM方法，对PWM波形进行了移相，使得ECR-SVPWM方法得到的实测相电流总谐波失真(total harmonic distortion,THD)比传统SVPWM提高了0.28%(从5.04%提高到5.32%)。

图21 SVPWM和ECR-SVPWM相电流波形FFT分析

3 结 论

针对传统SVPWM存在电流不可观测区域，无法获得可靠的相电流采样问题。提出一种通过随机数发生器对PWM波形进行移位，并完成电流零点漂移自校正的空间电压空间矢量脉宽调制方法。通过实验验证所提出方法的主要特性为：

1)消除了电流不可观测区域，实现电流的稳定可靠检测。

2)电流零点漂移自校正策略的引入，降低了电流零点漂移对于电流的影响，并提高电流检测精度，使得重构误差小于3.1%。

3)引入了不对称的PWM波形，THD有所提高，但仍保持在5.32%以下。