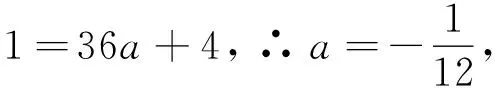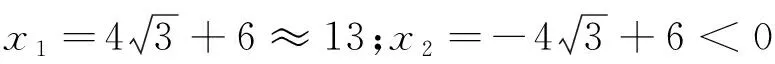利用数形结合求解不同类型的二次函数问题探索
顾 健
(江苏省海门市东洲国际学校,江苏海门,226100)
数形结合思想是数学学习中的重要思想方法,数与形的巧妙结合往往能使问题迎刃而解.诚如,著名数学家华罗庚所言:数缺形时少直观,形少数时难入微,数形结合百般好,隔离分家万事休.本文谈谈利用数形结合思想求解各种二次函数问题.
1 巧用数形结合求残缺型抛物线问题
“残缺型抛物线”是初中阶段常见的二次函数问题,考查难度不高,但需要同学们根据题目条件和图象发现正确的取值,本文所指的“残缺型抛物线”又叫不完整的抛物线.可以以抛物线的轴对称性和已知条件为依据获得解题思路,进而顺利求解.总的来说是根据已知条件表示出残缺的二次函数图象,再结合抛物线的特点解答相关问题.

图1
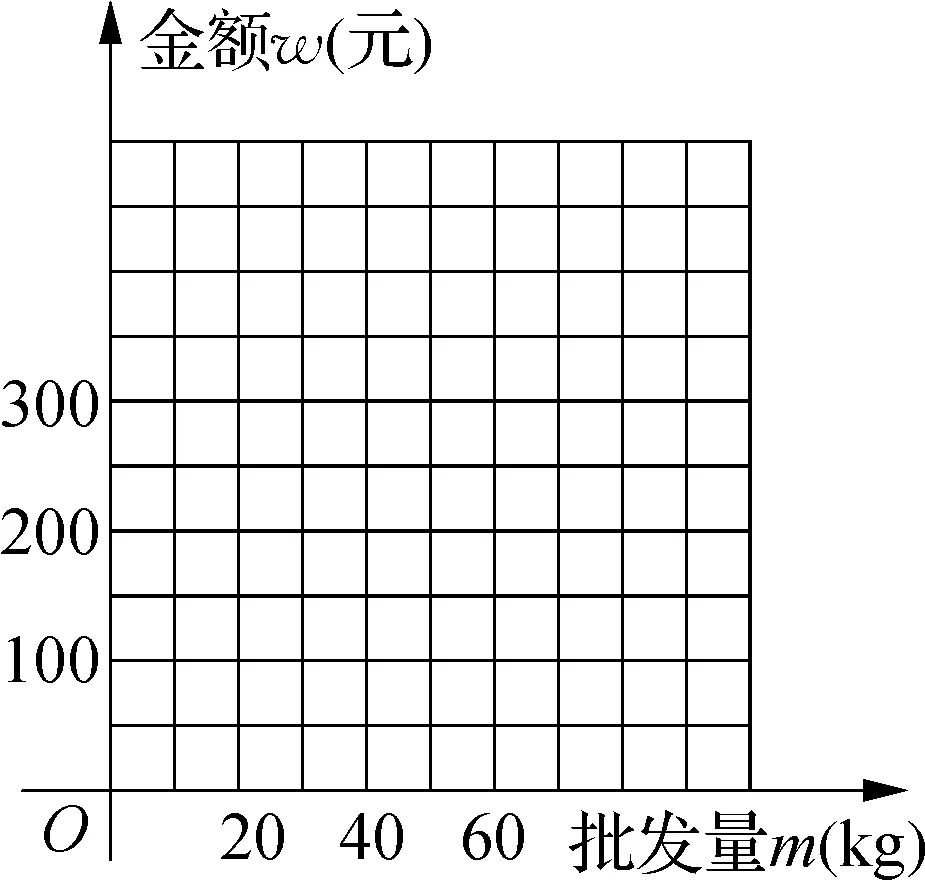
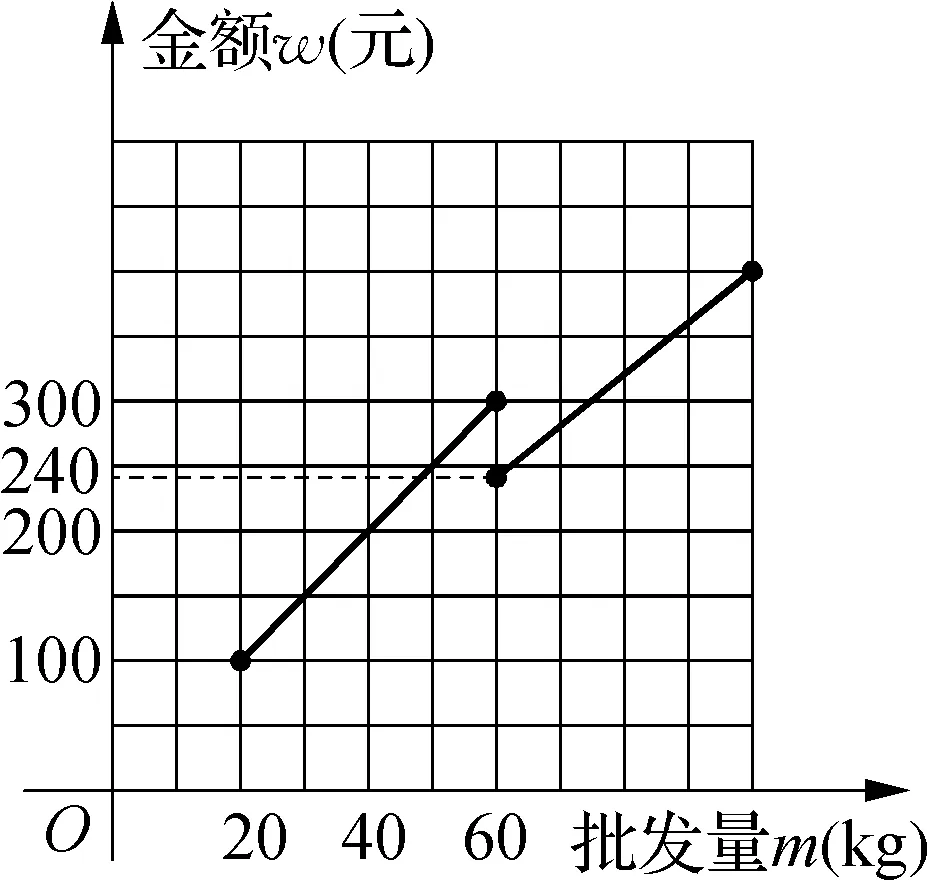
例1如图1所示,是二次函数y=ax2+bx+c图象的一部分,图象经过点A(-3, 0),x=-1是该函数的对称轴,且有以下四个结论:①b2>4ac;②2a+b=0;③a-b+c=0;④5a A. ②④ B. ①④ C. ②③ D. ①③ 思考:本题是要判断二次函数的三个系数之间的关系,已知函数的图象,根据图象的开口方向,图象与x轴的交点个数等判断三者之间的关系,进而得到正确答案. 解:由图象可得:图象顶点位于第二象限,且开口向下, 则抛物线一定和横坐标轴具有两个交点, 故Δ=b2-4ac>0成立,即①正确; ∵顶点位于第二象限,且已知x=-1时,a-b+c>0,∴③不正确; ∵抛物线的图象开口向下,∴a<0, 又∵b=2a,∴5a<2a,即5a 因此正确答案为B选项. 图2 练习1:如图2所示,是抛物线y=ax2+bx+c的一部分,其对称轴为直线x=1,若其与x轴一交点为B(3, 0),则根据图象可得,不等式ax2+bx+c>0的解集是. 思考:本题依旧属于“残缺型抛物线”,则根据纵坐标的右边推测出左边,根据抛物线开口向上,以及抛物线的对称性分析其解集取值范围,通过点A的坐标值确定其解集. 解:由图象可得:曲线与x轴有两个公共点,x=1是其对称轴,抛物线的开口方向向上, ∴对称轴右边的交点B与对称轴距离等于2, ∴抛物线和x轴的交点A与对称轴距离也等于2,∴(-1, 0)为A点的坐标, 故不等式ax2+bx+c>0的解集为x<-1或x>3. 图3 (1) 求该二次函数图象顶点的横坐标的取值范围; (2) 若该二次函数图象与x轴交于A、B两点,求线段AB长度的最小值. (2) 假设A(x1, 0),B(x2, 0), ∴x1、x2是方程ax2-bx+b=0的两根, 图4 练习2:如图4,二次函数y=(x+m)2+k-m2的图象与x轴有两个不同的交点,分别是A(x1, 0),B(x2, 0),与y轴的交点为C,设△ABC的外接圆的圆心为点P: (1) 与圆P相交时,求y轴的另一个交点D的坐标; 思考:本题主要考查一元二次方程的求根公式、根于系数的关系等,知识点较多,综合性叶强,如何表示OD和AB的长是本题的解题关键. 解:(1)根据题意易求得点C的坐标为(0,k), 由题设可知,x1、x2是方程(x+m)2+k-m2=0即x2+2mx+k=0的两根, ∴x1+x2=-2m,x1x2=k, ∵D作为⊙P与y轴的另一个交点,且⊙P的两条相交弦是AB、CD, 因此可以设点O为交点,连接DB, ∴△AOC∽△DOB, 由题意可得,在y轴的负半轴上存在点C, 因此,y轴的正半轴上存在点D, ∴(0, 1)表示D的坐标; (2) ∵AB⊥CD,AB刚好是⊙P的一条直径, ∴关于点O对称是C、D的对称点, ∴点C的坐标可以表示为(0,-1),即k=-1, 解之得:m=-2.(m=2舍去). 图5 关于二次函数的探究应用问题主要包括两个方面,一方面是二次函数与体育相关的问题,例如以球类为主要载体考查二次函数问题,增强学生将知识与生活相联系;另一方面是二次函数与经济相关的问题,此类型问题在一元二次方程和二次函数相联系的基础上运用二次函数及其图象和性质去解决现实生活中的一些问题.这类型问题的解答要注意结合实际情况确定自变量的取值范围,进而求解. (1) 求小球开始飞出到第一次落地时,该抛物线的解析式; (2) 小刚需要再向前跑多少米才能抢到落点D? 思考:本题可以通过建立函数模型求解,根据题意得到A点的坐标和最高点M的坐标,利用顶点式求出抛物线的关系式;(2)求小球第一次落地点与小刚的距离,等价于求这条抛物线和横坐标轴的交点的横坐标. 解:(1)如图所示,设第一次落地时抛物线的表达式为y=a(x-6)2+4, 由题意可得:当x=0是,y=1, ∴C的坐标为(13, 0), ∴BD=23-6=17 m. 练习3:如图6所示是某种水果的批发单价和批发量对应的函数关系图象,在下图的坐标系中画出该函数图象,并之处金额在上面范围内,以同样的资金可以批发到较多数列的该种水果. 图6 思路:根据题意得到相关方程组并确定自变量的取值,最后根据图象分析得到所求即可. 图7 图8 函数图象如图9所示,当以同样的资金可以批发到较多数量的该种水果时,资金金额应处于240 图9 对于一些错综复杂的问题,利用数形结合思想能够使得问题变得形象直观,解题思路更加清晰,一目了然.解答二次函数问题时灵活运用数形结合不仅可以增强对二次函数的基本性质与图象的理解,更能够让学生将数和形建立关系,使学生对二次函数的学习产生强烈的兴趣.
2 巧用数形结合求二次函数图象的“四点”“五距”



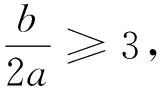
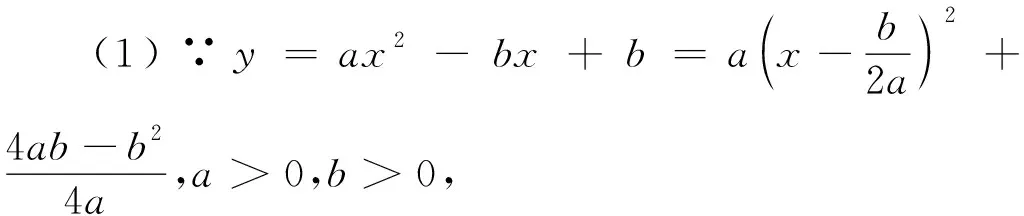



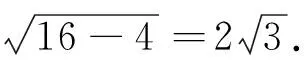



3 巧用数形结合解二次函数的探究应用问题