基于辩证思维的问题解决能力培养策略的思考

雷安桃

(凯里学院，贵州凯里，556000)

《义务教育数学课程标准(2022版)》指出：“通过数学的思维，可以揭示客观事物的本质属性；能够运用符合运算、形式推理等数学方法，分析、解决数学问题和实际问题；能够发展质疑问难的批判性思维.[1]”这说明从辩证的角度去分析问题，发展学生的批判性思维，培养学生的问题解决能力是十分重要的.本文以辩证思维为视角，对初中数学教学中如何培养学生问题解决能力进行思考和研究.

1 透过数学现象，抓住数学本质

1.1 概念与背景

透过现象看本质是辩证思维的一个重要方面，我们对事物的思考不能仅仅停留在表面，要学会透过表面去看到事物所固有的本质属性，在数学中，情境化、多变式的数学问题往往无法使学生透过情境抓住数学本质.

1.2 教学实施

学习数学知识和思考数学问题的过程中，不要被数学知识的表面现象所迷惑.要学会透过数学的现象去揭示其中的数学规律，并利用揭示的数学规律解决问题，提升解决一类问题的能力.

如何在教学中去引导学生透过图形这个现象去把握本质呢？例如在多边形内角和教学中，教师在进行多边形内角和练习中有这样一道问题：

(1) 求下列三个图形中∠A+∠B+∠C+∠D+∠E的度数.

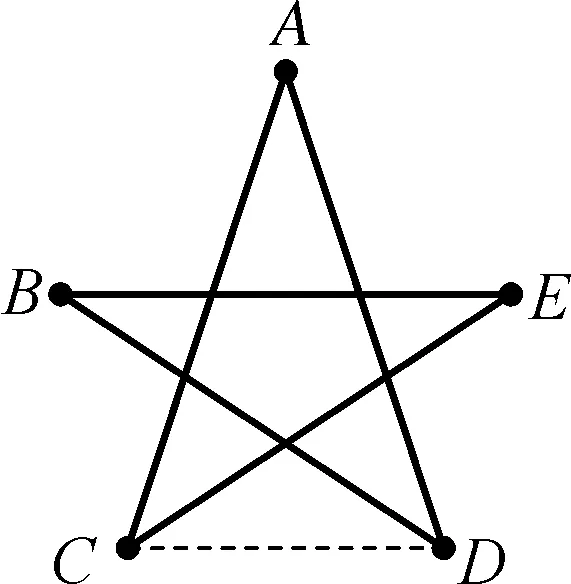
图1

图2

图3

(2) 求一下图形中∠B+∠C+∠D+∠E+∠F+∠G的度数.

图4

图5

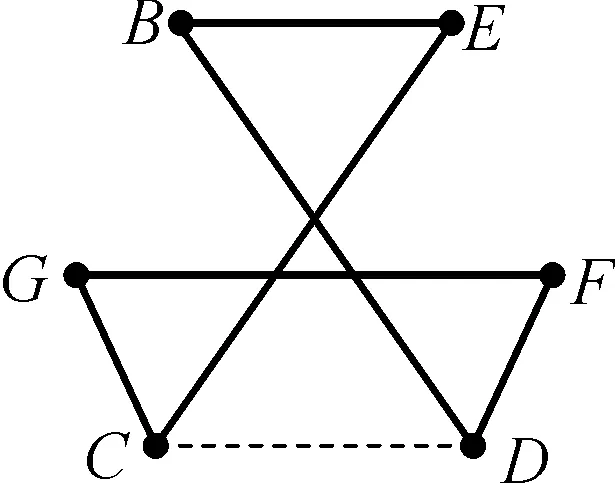
图6

问题1：这几个图形有什么样的联系？

通过观察我们可以发现图2是由图1中的点A转移到线段BE的下方，图3是由图1的点B和点E移到图形中间，图4、图5、图6分别是把图1、图2、图3中的顶点A切成线段GF，也就是说后面的五个图形都是由图1演变而来的，这是他们之间的联系.

问题2：既然它们之间有如此联系，如何进行转化呢？

连接线段CD，我们发现可以把第一题的5个角内角和转化为三角形求解，把第二题中的六个角的内角和转化成我们熟悉的四边形进行求解.

问题3：这6个图形都可以用什么方法进行求解？

多边形的内角和公式：(n-2)×180°进行求解.

在这个过程中我们透过这些不同图形的表象，揭示它们之间的本质是多边形的内角和，这种由此及彼、由表及里的思索，可以让学生们更好地揭示问题的规律.

2 化动为静，静观其变

2.1 概念与背景

辩证唯物主义告诉我们：运动是物质存在的方式和固有属性，是永恒的，绝对的；而静止则是相对的，暂时的，是物质运动的一种特殊形式，这就是运动和变化的观点[2].正如人在坐火车时，人没有感觉在动，却感觉到车窗外的树木和建设在飞快地往后倒退，这种“车静而物动”启发我们，有时候“静止”的状态是伴随着“运动”的，这也可以说化动为静，静观其变，我们只有在运动的事物中寻求相对的静止，才能去把握住事物的本质.在初中常见的问题中就是图形的动点问题.

2.2 教学实施

教学中要引导学生用运动和静止的观点去思考问题并解决问题，在看待问题的时候要多方面思考，走出自己固有的思维，在解决问题的过程中要学会变换看问题的思路，寻找多种多样的解题方法.

在教学中如何引导学生用运动和静止的观点解决问题呢？例如在初步讲动点问题专题中有这样一个问题：

如图，在梯形ABCD中，AD∥BC，AD=9 cm，BC=6 cm，点P从点A出发，沿着AD的方向向终点D以每秒一个单位的速度运动，当点P在AD上运动时，设运动时间为t，求当t为何值时，四边形APCB为平行四边形.

问题：如何用把运动的动点P化为静止的平行四边形？

最终是求APCB为平行四边形，所以可以利用平行四边形的性质去求得动点P移动的距离.

∵四边形APCB为平行四边形，

∴BC=AP且BC=AP，

∴AP=6，∴t=6.

这个题目是最简单的动点构成特殊图形类型，解决这一类动点构成特殊图形的问题，分析图形变化过程中变量和其他量之间的关系，或是找到变化中的不变量，确定特殊图形中动点的位置，画出符合题意的图形——化动为静，建立方程或函数关系解决动点问题.因此，在变化中找到不变的性质是解决“动点”探究题的基本思路，这也是动态几何数学问题中最核心的数学本质.在教学中确立这种“化动为静，静观其变”的观点，可以使学生在解题时开拓视野，对于提高学生思考问题、解决问题的能力着不可估量的影响.

3 代数与几何互化

3.1 概念界定与背景

唯物辩证法指出， 客观事物是发展变化的，不同事物间存在着种种联系， 各种矛盾无不在一定的条件下转化[3].著名数学家华罗庚曾经说过：“数形本是两依依，数缺形时少直观，形少数时难入微，数形相助双翼飞”.这说明在初中数学中，代数与几何是密不可分的，形成你中有我，我中有你.

3.2 教学实施

在遇到一些代数问题时，根据已知条件中特有的形式与特征，利用图形转化为几何问题有时候更利于解决问题.几何问题也是如此.在教学中我们如何去进行代数与几何的互化呢？例如在讲解一元二次方程组时，我们会利用图形法求解一元二次方程组所构成的区域面积.

问题：直线y1、y2的图形分别是怎么样的？与坐标轴相交后的图形面积怎么求？

这个问题是典型的代数问题，但是用代数思维我们无法快速求解，也就是如果借助函数图象学生很难做出来，所要先引导学生画出两条直线的图象，再去求交点问题和面积就很简单了.

根据图象可得交点P为(2， 1)

代数与几何是初中数学的主体内容，我们要在教学中渗透代数问题几何化，几何问题代数化的辩证思想，让学生学会对问题的转化，用不同的角度去思考问题，对问题进行数形结合，这对学生的解决问题能力十分重要.

4 联系与发展

4.1 概念界定及背景

唯物辩证法告诉我们，事物之间存在着普遍的相互联系，而且还在不断地变化与发展[3].在数学教学中，联系是指数学知识之间存在着某种共性，并且由此共性能发展成下一个知识点，知识点之间存在的包含关系.

4.2 教学实施

在教学中，我们不光是要学习一种知识，而是要从中找到知识的联系点发展为一类连贯知识，由点形成面，又能从面中准确找到点的位置，用联系与发展的观点看待知识，学生就会明白所学的知识都不是单独存在的、静止的，而是可以由点成面地存在着相互联系和变化发展的.例如在学完平行四边形一章节之后，要引导学生进行知识的总结，从中发现知识的联系与发展.

请你归纳一下本章我们所学的知识，试着寻找它们之间的联系点.

首先我们先从简单的平行四边形出发，由边的特性可以得到菱形，由角的特性可以得到矩形，而正方形又是特殊的矩形，由此我们可以发现菱形和矩形都是由平行四边演变而来，只不过一个是领边相等，一个是有一个为直角.由此让学生由一个点的知识点变成一个面的知识点，那学生在遇到有关矩形或菱形问题时就可以想到利用平行四边形的相关知识求解，学生的知识面广了，解决问题的能力自然就提升了.

5 可逆性思维

5.1 概念与背景

可逆思维是辩证思想的一部分，可逆是学生在遇到正向思维无法解决的问题时，要学会“倒”着思考问题，改变思考问题的角度的方向分析问题.

5.2 教学实施

在初中数学中，运用可逆思维解决问题还是很多的， 比如：完全平方差公式的逆运算，正比例函数与反比例函数等.在一般考试中出现正面解决问题的比较少，更多的是可逆的和综合性的.所以，教师在教学时，要有意识地引导学生对概念和公式进行剖析变式，培养其可逆性思维.比如在讲解完全平方公式(a+b)2=a2+2ab+b2时，有意识地引导学生对此公式进行逆用.

(1) 计算1.232+0.762+2.46×0.76；

问题：这三个题目怎么计算？

提示：(1)第一个题目直接就是完全平方公式的逆用，学生可自行完成.

分析：(2)对分母逆用平方差公式，这是学生思考该题目的难点，分母可以利用平方差公式解决.分母=(2 0082-1)+(2 0102-1)

=(2 008+1)(2 008-1)+(2 010+1)

(2 010-1)

=2 009×2 007+2 011×2 009.

至此，学生自然就能把这个问题解决了.

解决：(3)看着难其实简单.第一步利用完全平方差展开：第二步展开之后看这些式子有没有相似简便算法；第三步解决问题.

在课堂中对学生多进行可逆思维的训练，进行正逆向问题对比，学生能清晰地理解正问题的已知和所求正好是逆问题的所求和已知，解题思路相反，从列式上看运算也是互逆的.这样学生对应用题，特别是对逆问题的结构特征，有深刻的认识，可逆性思维又得到培养.培养学生的可逆性思维.

6 不可忽视的批判性思维

6.1 概念与背景

思维批判性的高层次表现为思维的论证性[4].拥有这种思维的学生看问题时总有自己独特的见解，善于思考为什么，喜欢发现问题并解决问题，他们会十分耐心地去判断问题的真实性和根据，从而去伪存真，揭示问题正确的因果关系.

6.2 教学实施

在数学教学过程中，在教学过程中进行反思训练，鼓励学生大胆质疑，引导学生进行辨析.教师要善于激发学生的批判性思维，多让学生想一想“为什么要这么做？”“这样的做法合不合理？”“怎样做才是对的？”

例如在反比例教学中，有这样一道练习题：

师：你为什么会想到这么做这个题目？

师：你觉得不等号的方向要改变吗？

生：不用改变.

师：为什么不用改变呢？

生：应该要改变吧，比较未知数的正负未定.

师：那你再想一想怎么做更合理呢？

生：可以分类讨论和画图象.

在上面的教学过程中，老师利用学生比较容易犯的错误，可以通过类似不断地询问学生为什么，引导学生进行多方面思考，培养了学生的批判性思维.

基于辩证思维培养学生解决问题的能力，不仅仅只是上面阐述的六点，中学数学中的辩证关系是十分丰富的，作为一名教师，不仅是传授知识，更重要的是通过知识的传授，去培养学生辩证思考问题的习惯，提高学生的辩证思维能力.因此，既要让学生在遇到问题时透过数学现象，抓住数学本质，也要让学生学会用运动和静止的观点看问题，寻找问题的联系与发展，在代数问题与几何问题中互化，对问题学会从反面思考，培养可逆思维，对问题要敢于质疑，培养批判性思维，最终达到更好地培养学生问题解决能力.