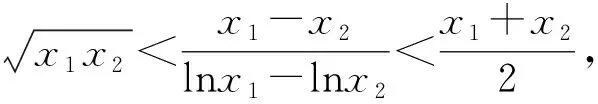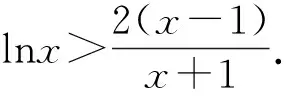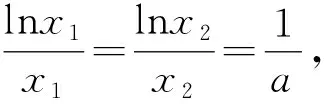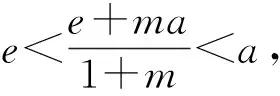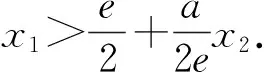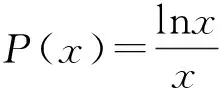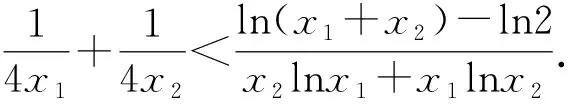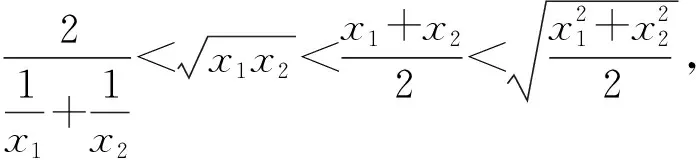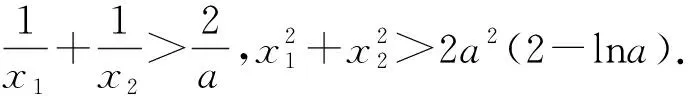双变量不等关系的几种构造角度及变式

江苏省海门中学 (226100) 蒯 龙

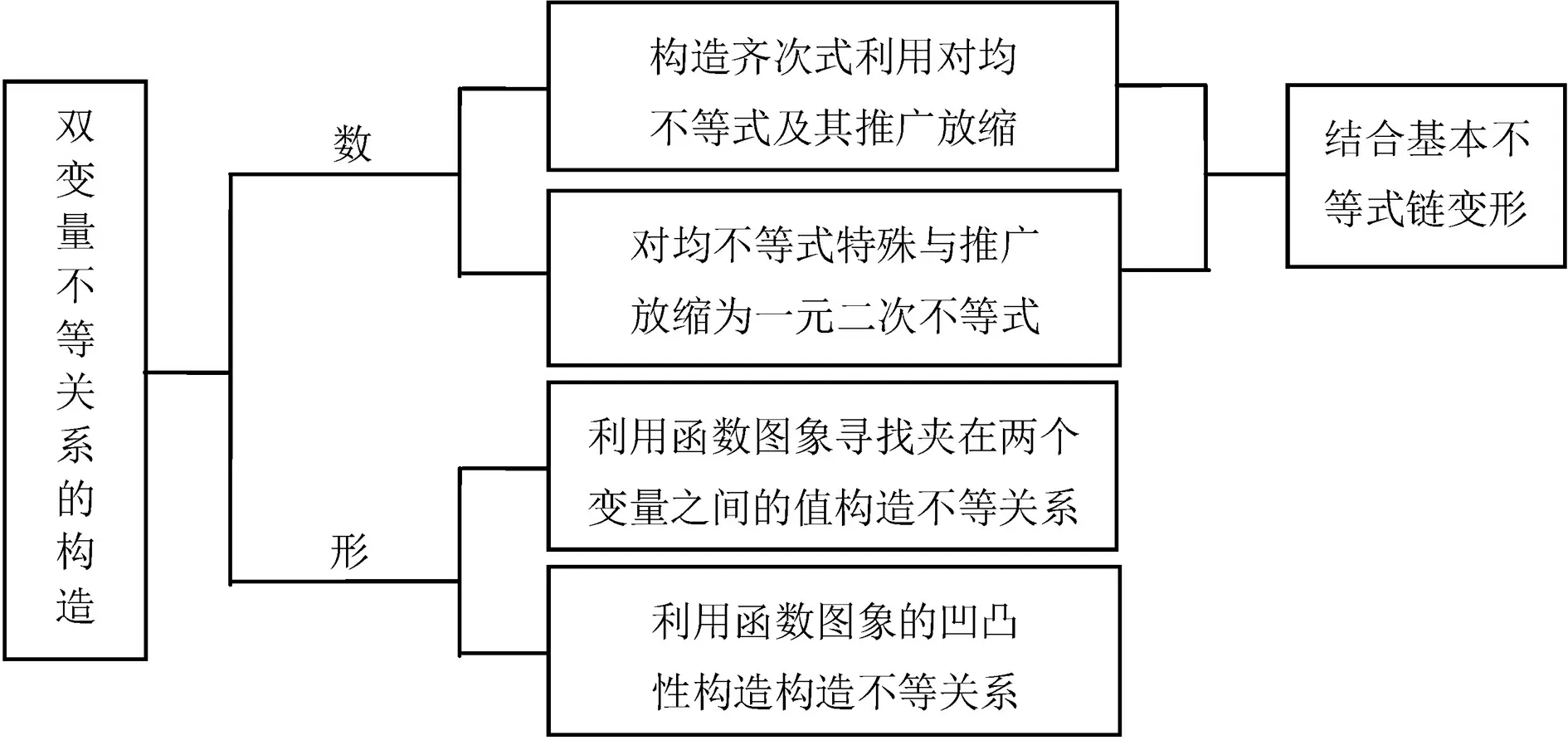
双变量不等关系的证明问题是考试中的热点问题，关于此类问题的解法研究的文章的很多，但是作为教师，不能仅仅满足介绍各种解法，而应更多讲清楚解法的来源、问题的本质、命题的角度，明晰命题者的意图.本文结合一道全国高中数学联赛预赛试题，从不同的角度构造双变量的不等关系，给出问题的变式，以期对此类问题有更全面的认识.

一、题目

(2021全国高中数学联赛福建预赛)已知f(x)=ex-xa，x>0，a∈R.(1)若f(x)≥0恒成立，求a的最大值；(2)若x1、x2是f(x)的两个零点，且x1>x2，求证：x1+x2>2a.

二、构造角度与变式

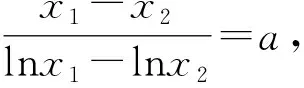
变题1 已知f(x)=ex-xa，x>0，a∈R.若x1、x2是f(x)的两个零点，且x1>x2，求证：x1x2

变题2 已知f(x)=ex-xa，x>0，a∈R.若x1、x2是f(x)的两个零点，且x1>x2，当e

变题3 已知f(x)=ex-xa，x>0，a∈R.若x1、x2是f(x)的两个零点，且x1>x2，求证：x1+ex2>3e.

变题4 已知f(x)=ex-xa，x>0，a∈R.若x1、x2是f(x)的两个零点，且x1>x2，求证：x1+x2>4a-3e.

从形的角度还可以采用切线放缩和切割放缩等构造，限于篇幅，不再赘述.