线性化思想在求导数单调区间的运用

广东省中山市桂山中学(528463)蔡晓波

导数是研究函数的重要工具,是高中数学中的学习重点和学习难点,很多学生对于导数有一定的畏惧感.而研究一个函数单调区间是认识和运用这个函数不可逾越的一步,而导数是研究函数单调性的强有力工具.但是很多学生对于复杂一点的,尤其是涉及到分类讨论的利用导数求函数单调区间问题就束手无策,无从下手.笔者基于学生的此种现实状况进行探究,发现对一类函数的导函数进行线性化可以有效的降低该类函数求单调区间的复杂性,现将探究结果呈现如下,望同行批评指正.

一、相关结论与证明

首先,我们先来看一个引理.

引理若函数f(x)与g(x)是具有相同定义域的连续单调函数,且具有相同的零点,相同的单调性,则不等式f(x)＞0(＜0)的解集与g(x)＞0(＜0)的解集相同.

证明下面仅证明f(x)＞0的解集与g(x)＞0的解集相同.设函数f(x),g(x)的定义域均为D,设x0为f(x)的零点,故f(x0) = g(x0) = 0,因为函数f(x)与g(x)具有相同单调性,故不妨设f(x)为单调增函数,故g(x)也为单调增函数,故f(x) = 0与g(x) = 0均有唯一的实数根x0.

(1)若f(x)＞0的解集为∅,此时若g(x)＞0不为空集,不妨设g(x1)＞0,(x1∈D),故g(x1)＞g(x0),结合g(x)单调性可得x1＞x0;故f(x1)＞f(x0) = 0,故x1为f(x)＞0的一个解,与f(x)＞0的解集为∅矛盾,故g(x)＞0的解集也为∅.反之可得g(x)＞0的解集为∅时f(x)＞0的解集也为∅.

(2)若f(x)＞0的解集不为∅,不妨设f(x)＞0的解集为D1,由(1)可知此时g(x)＞0的解集也不为空集,设为D2.设任意x1∈D1,则f(x1)＞0 = f(x0),结合单调性可得x1＞x0.由g(x)为增函数可得g(x1)＞g(x0) = 0,故x1∈D2,故D1⊆D2.同理可证: D2⊆D1,故D1= D2.同理可证:证明f(x)＜0的解集与g(x)＜0的解集相同.

综上可得:不等式f(x)＜0(＞0)的解集与g(x)＜0(＞0)的解集相同.

结论若函数fi(x)与gi(x), i∈{1,2,3,···,n}是具有相同定义域Di的连续单调函数,且具有相同的零点,相同的单调性,且Di= D ≠∅,则不等式fi(x)＞0(＜0)的解集与gi(x)＞0(＜0)的解集相同.

证明下面用数学归纳法证明该结论.

(1)由引理可得当n = 1时结论成立.

设fk+1(x)＞0的解集为S0, fk+1(x)＜0的解集为T0,故

利用结论,不难证明出该推论,故这里不再赘述,相关证明留给读者完成.

利用该推论,我们可以对一类涉及讨论的,需要利用求导讨论函数单调区间的问题进行线性化,从而降低复杂度,使得学生容易理解,不易出错.

二、例题实践

例1(2017年高考全国I卷第21题改编)已知函数f(x) = ae2x- (a + 2)ex+ x.

(1)讨论f(x)的单调性; (2)略.

分析对f(x)求导可得: f′(x) = (aex-1)(2ex-1),若不对其线性化处理,学生对该形式容易产生畏惧感,形式比较复杂,容易出错,但是如果我们利用结论及其推论对其线性化后,便可化为熟悉的一次函数或者二次函数的形式.

解对f(x)求导可得f′(x) = (aex- 1)(2ex- 1),显然y = 2ex- 1为增函数且有唯一零点x =

评注本题在a＞0的情况中,通过线性化把问题转化为二次函数的形式,而二次函数学生比较熟悉,能有效的降低单调区间讨论的复杂性.

例2(2018年辽宁朝阳高三一模(文) )已知函数f(x) =(常数a＞0).

(1)讨论f(x)的单调性; (2)略.

分析对f(x)求导可得: f′(x) = (x - a)lnx,故在分析f′(x)正负情况时,可以对lnx进行线性化处理,另外此题要注意f(x)的定义域.

解对f(x)求导可得f′(x) = (x-a)lnx,显然y = lnx为增函数,且有唯一的根x = 1, f′(x)正负情况等价于分析g(x) = (x - a)(x - 1),(x＞0)的正负情况.

1.当0＜a＜1时,当x∈(a,1)时, g(x)＜0⇔f′(x)＜0;当x∈(0,a),(1,+∞)时, g(x)＞0⇔f′(x)＞0;故f(x)在(a,1)单调递减,在(0,a),(1,+∞)单调递增.

2.当a = 1时, g(x) = (x - 1)2≥0,故f(x)在(0,+∞)单调递增.

3.当a＞1时,当x∈(1,a)时, g(x)＜0⇔f′(x)＜0;当x∈(0,1),(a,+∞)时, g(x)＞0⇔f′(x)＞0;故f(x)在(1,a)单调递减,在(0,1),(a,+∞)单调递增.

综上所述,当0＜a＜1时, f(x)在(a,1)单调递减,在(0,a),(1,+∞)单调递增;当a = 1时,故f(x)在(0,+∞)单调递增;当a＞1时,故f(x)在(1,a)单调递减,在(0,1),(a,+∞)单调递增.

评注在对导函数进行线性化分析正负之前,一定要先观察原函数的定义域,在前边的结论与推论中,我们均要求定义域相同.

例3已知函数

讨论f(x)的单调性.

分析对f(x)求导可得:

显然当a≤0时, ex-3a＞0,ex-a＞0,故仅需分析x-2a的正负情况即可,故不难得出f(x)在(-∞,2a)单调递减,在(2a,+∞)单调递增;而a＞0时, y = ex-3a单调递增且有零点x = ln(3a), y = ex- a单调递增且有零点x = lna;根据推论可得分析

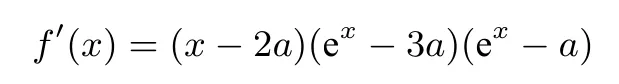
的正负情况等价于分析

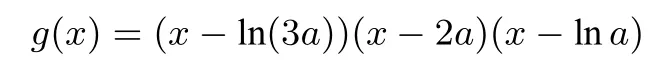
的正负情况;另一方面,根据a＞0不难证出

故根据“数轴穿根法”[1]便可很快的求出f(x)的单调区间情况为: f(x)在(lna,ln(3a)),(2a,+∞)单调递增,在(-∞,lna),(ln(3a),ln(2a))单调递减.

解略,由读者根据以上分析自己完成.

评注此题如果不把导函数进行线性化,学生在分析导函数f′(x)的正负情况时便会产生一定的畏惧感,容易算错;而如果根据推论把导函数f′(x)线性化后,问题就转化为学生熟悉的高次线性不等式的分析问题.

三、结论的运用范围与要注意的地方

上述例1-3均具有共同的特征:导函数能因式分解为有限个明确单调性或者明确恒大于(等于)零或恒小于(等于)零的因式相乘除.

因此,具备有上述特征我们便可以用本文的结论(推论)对其进行线性化,从而化为熟悉的高次线性不等式来分析问题.

在线性化过程中特别要注意两点: (1)线性化前后单调性一致; (2)线性化前后零点一致; (3)线性化前后定义域一致.

四、教学效果分析

笔者以中山市桂山中学水平相当,选科组合相同的6个班级为例进行试验.班级情况如下:

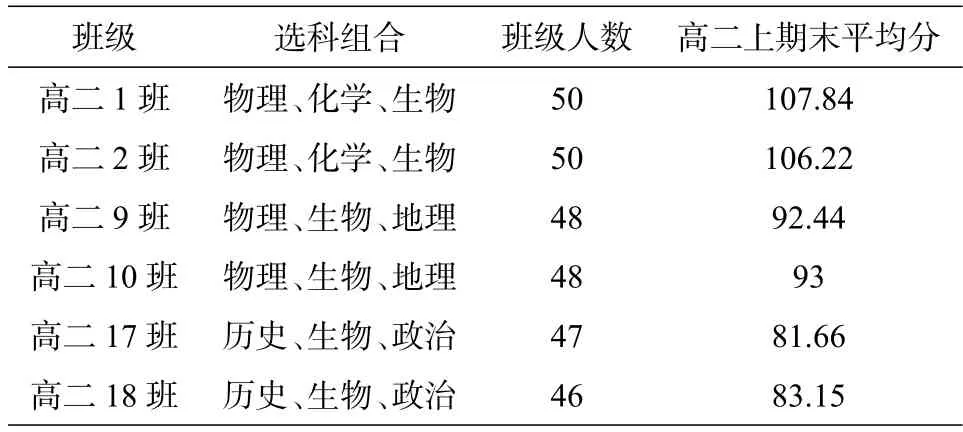
表1 中山市桂山中学参与试验的班级基本数据

笔者任教的班级为1, 2班, 2020年3月份由于疫情原因,本校学生均是利用钉钉进行线上教学,因此,笔者联系年级管理人员与相关班级的数学老师,在讲授“函数的单调性与导数”本节新课时,把1, 9, 17班的数学老师设置为同一个老师,为笔者本人.把2, 10, 18班的数学老师设置为同一个老师,也为笔者本人.笔者在上述的奇数班级讲授了线性化的方法,在偶数班讲授了以往的常规分析方法.

五月底返校复学一周后,笔者对上6个班的学生要进行一次“函数的单调性与导数”的测验,测试题目为本文前面所列的3个例题,内容均为考查单调性的讨论,其中例1,例2,例3分值分别为5分, 5分, 10分,测试时间为25分钟,测试的成绩如下表:

表2 参与“函数的单调性与导数”测试的班级的测试情况

据此,我们可以看出线性化思想对于具有“3”中总结的特征的题目十分有用,可以有效的降低了该类函数求单调区间的复杂性,特别是当导函数中有零点的因式越多时,线性化思想就越有用.另外,我们对以上数据统计得到如下2×2列联表[2]:

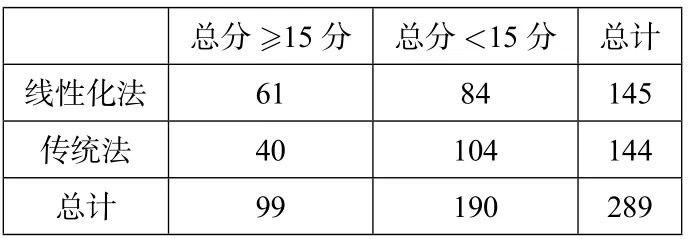
表3 测试成绩统计出来的2×2列联表

根据独立性检验我们可以计算得到

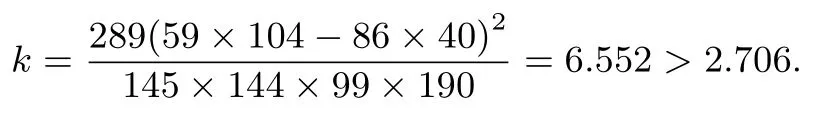
因此在犯错误率不超过0.1的前提下,可以认为本文所讲的“线性化法”与学生是否能掌握具有“3”中总结的特征的题目有关系.