看似巧合 实为必然—一道堵车次数的数学期望与方差引发的探究

湖南省怀化市精楷英复读学校(418000);湖南省会同县第一中学(418300) 于先金

湖南省会同县第一中学(418300) 李林雕

一、试题呈现,问题解析

题目如图1,某工人的住所在A处,上班的企业在D处,上下班的路线有三条路程几乎相等的路线供选择:环城南路经过路口C,环城北路经过路口F,中间路线经过路口G.如果开车到五个路口B, C,E, F, G因遇到红灯而堵车的概率分别再无别的路口红灯.

图1

(1)为了减少开车在路口因遇到红灯而堵车的次数,这位工人应选择哪条行驶路线?

(2)对(1)所选择的路线,求其堵车次数的方差.

这是教辅书《三维设计(选择性必修第3册)》(南方出版社, 2021年8月)第4页中的一道例题,各路口因遇到红灯而发生堵车事件是相互独立的,利用相互独立事件的概率公式可求出一条路线因遇到红灯而发生堵车X次的概率,进而可求出随机变量X的数学期望和方差,最后行驶路线的选择由堵车次数X的数学期望的大小来确定.

二、参考答案,通性通法

解(1)设这位工人选择行驶路线A - B - C - D,A - F - E - D, A - B - G - E - D分别堵车X1, X2, X3次,则X1,2= 0,1,2,X3= 0,1,2,3.

由于

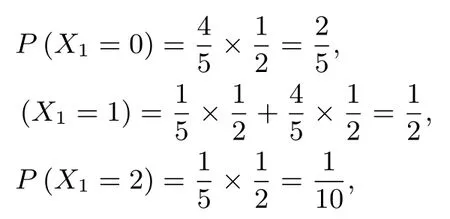
则X1的数学期望为

由于

则X2的数学期望为

由于

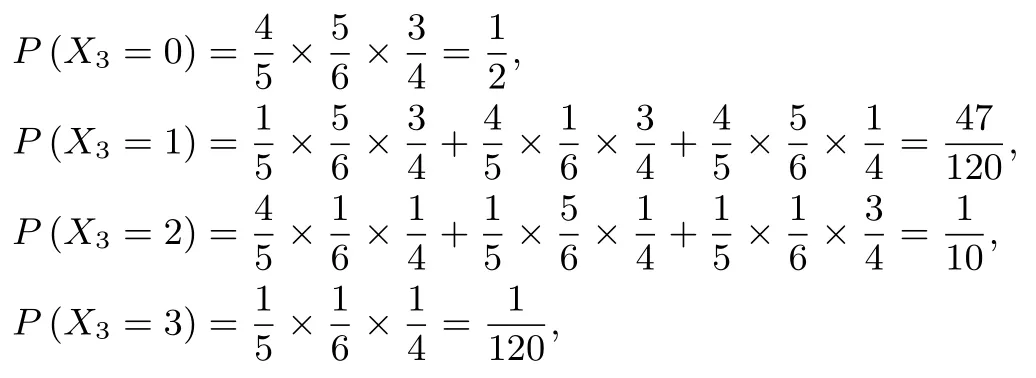
则X3的数学期望为

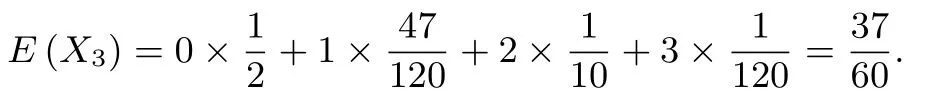
比较知E(X2)最小,所以这位工人应选择行驶路线A - E - F - D.

点评本题考查相互独立事件的概率和离散型随机变量的数学期望和方差,易错点是题中出现的道路情况比较多,稍有不慎计算就会出错.

三、提出疑问,探究求证

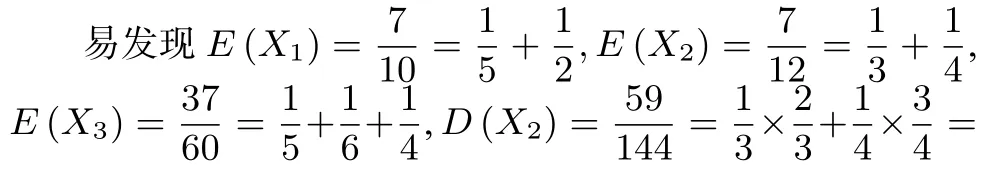
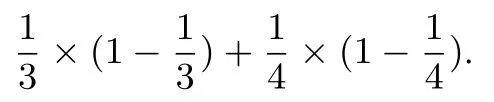
这是巧合还是必然?若开车到五个路口B,C,E,F,G因遇到红灯而堵车的概率分别为α,β,γ,m,n,则是否有E (X1) =α+β, E (X2) = m +γ, E (X3) =α+ n +γ,D (X1) =α(1-α)+β(1-β),D (X2) = m(1-m)+γ(1-γ),D (X3) =α(1 -α) + m(1 - m) +γ(1 -γ).

由于

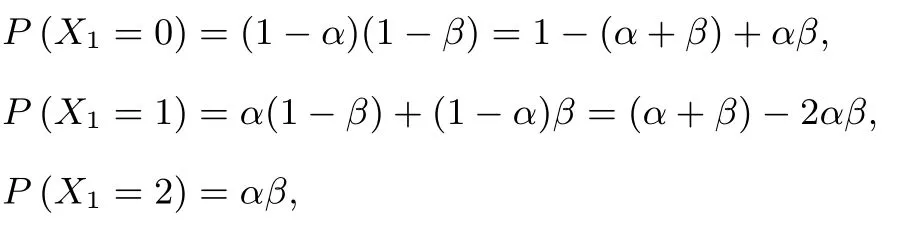
所以X1的数学期望与方差分别为

展开化简、整理得D (X1) =α(1 -α) +β(1 -β).

同理可证其它几个结论.

四、归纳总结,得出结论

定理从A地开车到B地,经过n个路口A1, A2,···,An,因遇到红灯而堵车的概率分别为p1,p2,···,pn,发生堵车的次数为X,则

从而E (Xi) = pi,D (Xi) = pi(1 - pi).

当i ≠ j时, Xi= Xj= 1⇔XiXj= 1,所以XiXj的分布列为

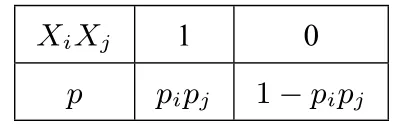
从而E (XiXj) = pipj.所以

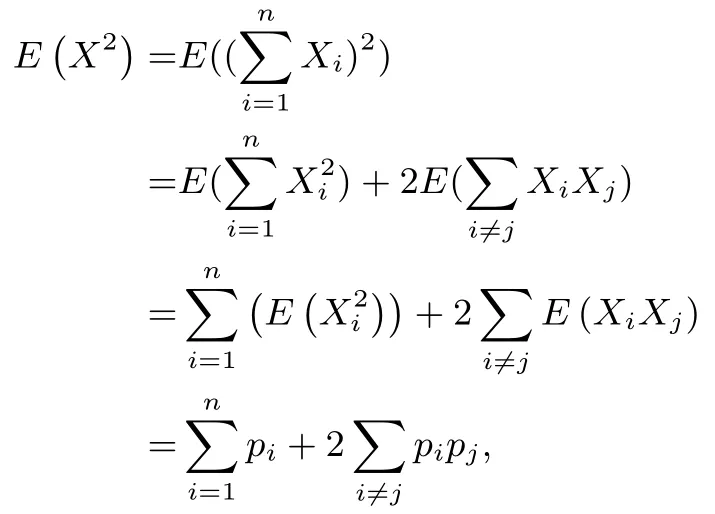
由方差的性质得

波利亚语:“没有一道题目是可以解决得十全十美的,总剩下一些工作要做,经过充分的探讨总结,总会有点滴的发现,总能改进这个解答,而且在任何情况下,都能提高自己对这个解答的理解水平”.

五、试题链接,提升能力

广东省2012年高考理科数学仿真模拟试题:

图2

张先生家住H小区,他工作在C科技园区,从家开车到公司上班路上有L1, L2两条路线(如图), L1路线上有A1,A2, A3三个路口,各路口遇到红灯的概率均为; L路线上2有B1, B2两个路口,各路口遇到红灯的概率依次为

(I)若走L1路线,求最多遇到1次红灯的概率;

(Ⅱ)若走L2路线,求遇到红灯次数X的数学期望;

(Ⅲ)按照“平均遇到红灯次数最少”的要求,请你帮助张先生从上述两条路线中选择一条最好的上班路线,并说明理由.

答案(I)选择L2路线上班最好.