例说含参零点问题的突破策略

华南师范大学数学科学学院(510631) 陈伟连

1 问题背景

含参函数零点问题常见的题型有已知函数零点个数求参数的取值范围,或由已知条件讨论函数的零点个数.该类题型以函数零点的概念、函数零点存在性定理、函数的图象、函数的性质和函数与导数等知识点为背景,考查学生的直观想象能力、推理论证能力和运算求解能力,能有效检测学生的逻辑推理与数学运算等核心素养,体现了分类讨论、化归转化、数形结合、函数与方程等数学思想方法.基于以上特点,含参函数的零点问题不仅是函数与导数专题的重要内容,也是高考命题的热点和重点.

作为考生在高考备考中的常规训练,教师如果能在解题教学中让学生会一道题而通一类题,那么备考工作将事半功倍,避免迷失在题海战术的海洋里.本文将利用一道含参函数零点问题,总结解题策略,分析各种策略存在的易错点和难点及相应的突破策略,揭示题目的本质和命题的角度,希望能够为教师的教和学生的学提供一点启示.

2 问题展现

题目已知函数f(x) = lnx - ax2+ ax恰有两个零点,则实数a的取值范围为( )

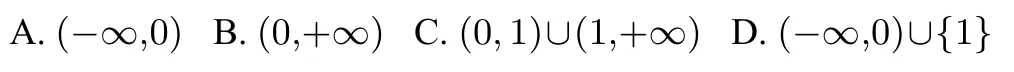
3 解题策略

3.1 特值法

作为选择题,本题可在观察题目选项之后,利用特值法排除不合题意的选项,从而快速得到正确选项,培养学生“小题小做”的解题智慧.

解①当a = 1时, f(x) = lnx - x2+ x,

当0＜x＜1时, f′(x)＞0,当x＞1时, f′(x)＜0.即f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.所以fmax(x) = f(1) = 0,此时函数f(x)只有一个零点(如图1),不合题意,排除B, D.

图1

②当a = -1时, f(x) = lnx + x2- x, f′(x) =+ 2x - 1 =＞0恒成立,且f(1) = 0.所以f(x)至多只有一个零点(如图2),不合题意,从而排除A.故选C.

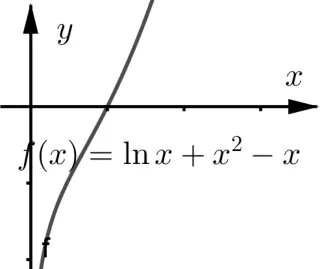
图2

评注在选择题中使用特值法可以极大减少运算量,缩短解题时间.当a = -1时,都不需要算出f(1) = 0,即可判断选项A不符合题意.

3.2 分类讨论法

分类讨论法处理含参函数零点的问题需要准确把握分类讨论的分界点.首先应该关注导函数的符号来讨论函数的单调性,具体而言即关注:导函数是否有根、根是否在定义域内以及根的大小.接着关注特殊位置的函数值,特殊位置包括:极值点处、区间端点处以及极限位置.考虑了以上因素之后,就能够做到不重不漏地对参数值进行分类和讨论.

解由题知

f′(x) =- 2ax + a =(x＞0).

①当a = 0时, f′(x) =＞0,f(x)在(0,+∞)单调递增,且f(1) = 0,所以f(x)只有一个零点,不合题意;

②当Δ= a2+ 8a≤0,即-8≤a＜0时,-2ax2+ ax + 1≥0.即f′(x)＞0恒成立,所以f(x)在(0,+∞)单调递增,且f(1) = 0,所以f(x)只有一个零点,不合题意;

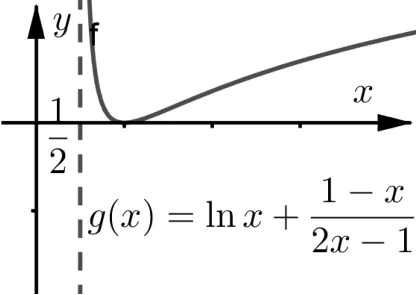
图3

综上所述, a的取值范围为a＞0且a ≠ 1.

评注上述分类讨论做法存在难点.难点一在于极值点处函数值符号的判断,此时需要利用隐零点代换消去参数,构造新函数求最值以判号;难点二在于极限位置函数值符号的判断,此时需要适当取点进行判号,或者利用函数类型的增长速度进行判断(增长速度:指数型＞多项式型＞对数型).

3.3 分离函数法

3.3.1 分离为两曲线

该类方法的关键是将原函数分离成两个函数图象为曲线的函数,于是接下来可以根据函数的凹凸性,初步确定参数的分类,接着根据使其具有公切线的临界情况,进一步对函数进行分类.具体操作如下:

解函数f(x) = lnx - ax2+ ax恰有两个零点⇔方程lnx = ax2- ax恰有两个实根⇔y = lnx与y = ax2- ax恰有两个交点.

①当a = 0时, y = lnx与y = 0只有1个交点.

②当a＜0时, y = lnx与y = ax(x - 1)只有1个交点.

③当a = 1时,因为lnx≤x-1,且x2-x-(x-1) =(x - 1)2≥0,所以x2- x≥x - 1≥lnx.此时y = x - 1恰好是y = lnx与y = x2- x的公切线,切点都为(1,0),所以y = lnx与y = x2- x只有1个交点.

④当a＞1时,此时y = a(x2- x)的开口变小,y = lnx与y = a(x2- x)有2个交点,其中一个横坐标为1,另一个在(0,1)内.

⑤当0＜a＜1时,此时y = a(x2- x)的开口变大,y = lnx与y = a(x2- x)有2个交点,其中一个横坐标为1,另一个在(1,+∞)内.

综上所述, a＞0且a ≠ 1.

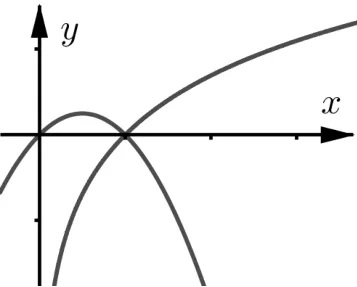
图4

图5

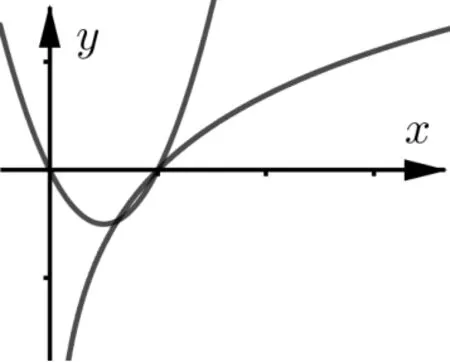
图6

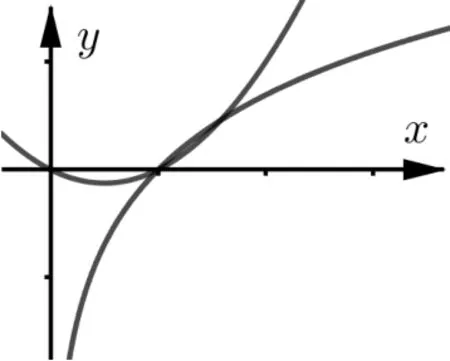
图7

评注该解法中,当a = 0时,不是两曲线,单独考虑;当a＜0时,两个函数都是凹函数,且没有公切线;当a＞0时,y = lnx为凹函数, y = a(x2- x)为凸函数,于是以当a = 1时有公切线作为临界点进一步分类讨论.这不仅是一种解题策略,同时也是该类题目的命题方法.如:选定一个凸函数y = ex,然后确定含参二次函数y = ax2+ b′x + c′,求出其公切线的情况,于是就能得到如下高考题:

题目1(2018年高考全国II卷理科第21题)已知函数f(x) = ex- ax2, (1)略; (2)若f(x)在(0,+∞)上只有一个零点,求a的值.

题目2(2017年高考全国I卷理科第21题)已知函数f(x) = ae2x+ (a - 2)ex- x, (1)略; (2)若f(x)有2个零点,求a的取值范围.

3.3.2 分离为一直线和一曲线

该类方法中,分离后的参数在新的函数中一般会有明显的几何意义,于是可以根据参数的几何意义,结合函数的图象对参数进行分类讨论,判断两函数图象的交点个数,从而求出符合零点个数条件的参数范围.具体操作如下:

综上所述, a＞0且a ≠ 1.

评注解题过程中的“注意到”是需要去计算的,涉及“过一点求已知曲线的切线”的知识点.该类方法较为简单,思维量少,但学生在绘制分离出来的函数图象时容易出错,出现将y =在(e,+∞)上单调递减时穿过x轴的情况.此外,该类解题策略也是命题方法:选定一个凹函数或者凸函数,过一点求其切线,然后将斜率设置为参数,进行命题.如:令f(x) = ex(凸函数), g(x) = k (x - x0),讨论函数F(x) = f(x) - g(x)的零点个数,则可以命制出如下高考题:

题目3(2020年高考全国I卷文科第20题)已知函数f(x) = ex-a(x+2). (1)略; (2)若f(x)有两个零点,求a的取值范围.

还可以将x0换为参数k,改变函数f(x),如令f(x) =x3,g(x) = k(x - k),讨论函数F(x) = f(x) - g(x)的零点个数.可以命制出以下高考题:

题目4(2020年高考全国III卷文科第20题)已知函数f(x) = x3-kx-k2. (1)略; (2)若f(x)有3个零点,求k的取值范围.

3.4 分离参数法

利用该解法的关键是利用导数和极限的知识准确地画出分离出来的函数的大致图象,求其值域,然后利用y = a或y =与分离出来的函数的交点个数,讨论零点的个数,具体如下.

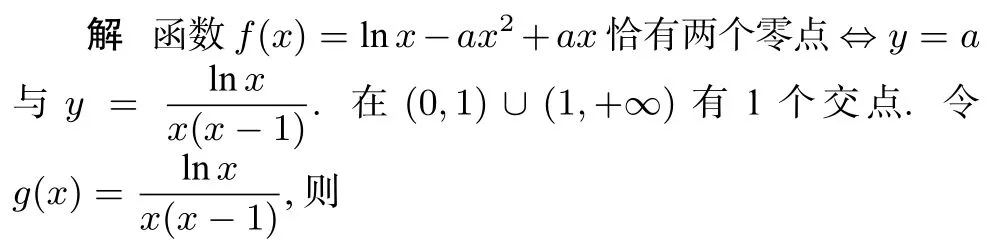
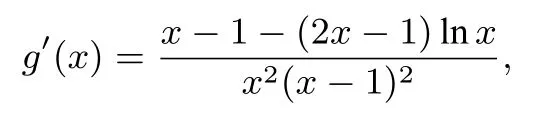
令h(x) = (x - 1) - (2x - 1)lnx,则

h′′(x) = -＜0,所以h′(x)在(0,+∞)上单调递减,注意到h′(1) = 0,故当0＜x＜1时, h′(x)＞0,当x＞1时, h′(x)＜0,所以h(x)在(0,1)上单调递增,在(1,+∞)单调递减,故h(x)≤hmax(x) = h(1) = 0,从而g′(x)≤0,所以g(x)在(0,1)和(1,+∞)上单调递减.当x→0+时,g(x)→+∞;当x→+∞时, g(x)→0,当x→1时,由洛必达法则可知:

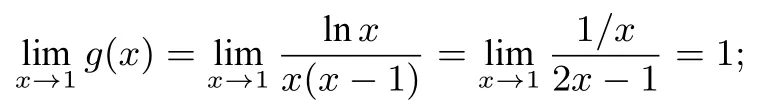
评注利用分离参数法解决含参零点问题往往能够将复杂的分类讨论转化成平行与x轴的直线与函数的交点个数问题,使问题简化,降低思维量.但是,其难点在于分离出来的函数的刻画,有时候需要涉及到多次求导和高等数学中的洛必达法则刻画函数图象.

4 突破策略

每种解题策略都有相应的易错点与难点,值得引起我们的注意,这给出其类型和相应的突破策略,但不详细叙述.

方法易错点突破策略难点突破策略分类讨论法忽略二次项系数为0的讨论明确二次函数的定义,强调分类讨论要不重不漏①分类讨论的标准①教好分类讨论的5个标准及原因②隐零点两端函数值正负的判断②取点问题(放缩)②′利用函数的级别去判断极限值(指数型＞多项式型＞对数型)③极值正负符号的判断③隐零点问题(消参)构造新函数分离函数法一(两条曲线)分类讨论的标准关注两个函数的固定交点处的公切线斜率分离函数法二(直线与曲线)函数图象画错关注图像的极限情况:是否穿过x轴分离参数法忽略分离参数之后出现消根的情况关注分离参数之后的定义域变化函数图象极限位置的绘制洛必达法则