一道圆锥曲线模考题的解法探究及拓展

华南师范大学数学科学学院(510631) 曾文佩

1 原题呈现

(1)求C的方程;

(2)已知点F (1,0),直线l : x = 4与x轴的交点为D.直线AM与l交于点N,是否存在常数λ,使得∠MFD =λ∠NFD?若存在,求λ的值.若不存在,说明理由.

2 解法探究

第(1)问直接设点M的坐标,利用斜率关系即可求得C的方程,主要探讨第(2)问的解法.

综上所述,存在常数λ= 2,使得∠MFD = 2∠NFD.

注记解法一的一方面将直线AM的斜率看做变量,由斜率的变化引起点M和点N的变化,可用斜率k来表示M和N的坐标,进而表示∠MFD与∠NFD的正切值.另一方面,通过特殊点,先猜想λ的值,再利用正切的二倍角关系来得到一般情况下的两角关系.此解法中的斜率k并不需要求出,蕴含了设而不求的想法.

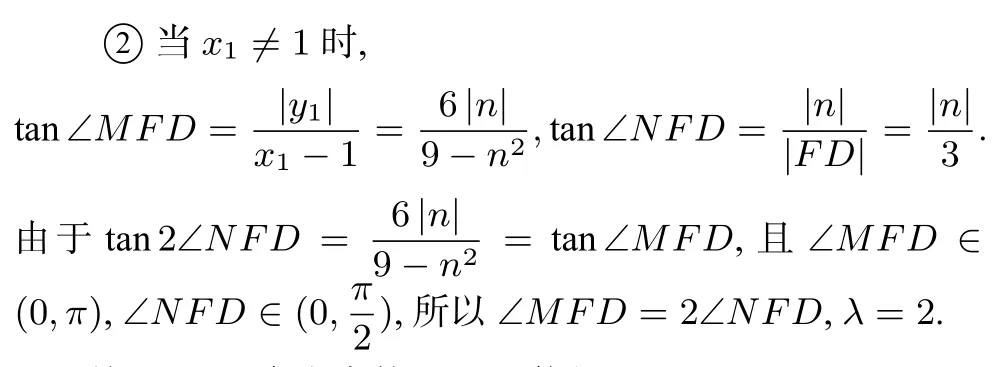
综上所述,存在常数λ= 2,使得∠MFD = 2∠NFD.

注记解法二与解法一类似,也是利用正切的二倍角关系来得到两角的关系.不同之处在于,此解法将点N看作是变量,由点N的纵坐标n的变化引起点M的变化,故用n来表示∠MFD与∠NFD的正切值,对n同样采取设而不求的做法来处理.

心理学家利昂·费斯廷格认为，跟其他人比较是一种本能的欲望。通过比较，我们才能找到自己所处的社会地位，向着更好的地方憧憬追逐，面对不如我们的人会让我们有牢固的安全感和幸福感。

易知点N到直线FD的距离为|ND| = |n|,所以d = |ND|,所以NF平分∠MFD,即∠MFD = 2∠NFD,故λ= 2.

注记解法三利用了角平分线的判定定理,通过求出点N到两边的距离相同证明NF是角平分线,从而得到∠MFD与∠NFD的关系.运用此解法解题,应先判断出关系,大胆猜想,小心验证.

注记此解法注意到直线l很特殊,是椭圆的右准线,可运用椭圆的第二定义得到一些线段比例关系,而外角平分线定理联系了线段比值和角,因此可考虑应用三角形外角平分线定理的逆定理,得到两角的关系.

图1

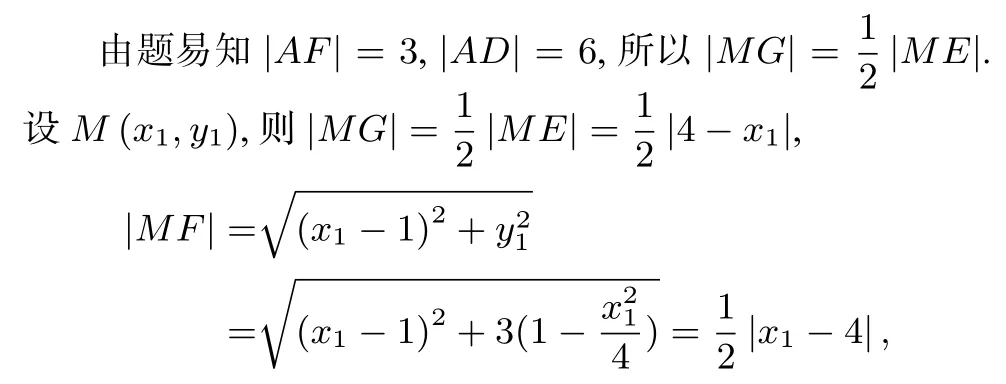
所以|MG| = |MF|,所以∠MFG =∠MGF.又因为∠MGF =∠GFD,所以∠MFG =∠GFD,即∠MFD =2∠NFD,故λ= 2.

注记解法五几乎完全是从平面几何出发,利用平行线的性质和相似三角形的性质以及等腰三角形的性质等,还运用了解析几何中的两点间距离公式,直接证明∠MFG =∠GFD,从而得到∠MFD与∠NFD的关系.

注记解法六从向量的角度出发,由向量的平行四边形法则和菱形的性质(菱形的对角线平分每一组对角),可知两单位向量的和向量所在直线恰好平分角∠MFD,通过证明和向量与的位置关系,从而得到FN是∠MFD的角平分线.此解法是向量在几何中的应用,体现了向量的强大功能.

在解析几何问题中,一般可以从多个角度入手,常用的解析法思路比较清晰,但一般会有较大的运算量,需要具备良好的运算能力;而几何法则在一定程度上减少了计算量,但更强调需要有良好的推理能力.解析法与几何法的结合往往能达到事半功倍的效果.

3 题目溯源

通过查阅文献,在文[1]中找到了本题所考察的椭圆的性质.文[1]的性质6证明了如下的一个关联椭圆准线的性质:

性质(文[1]性质6)如图2,设F (-c,0)为椭圆= 1(a＞b＞0)的左焦点,不过点F的直线与椭圆交于A、M两点,且与椭圆的左准线l交于N,则NF平分∠AFM的外角.

图2

图3

此性质的证明可类似第(2)问的解法四得到.当上述点F为右焦点、直线l为右准线、点A为左顶点时,对应的结论就是本题第(2)问考察的角的关系,即如下推论:

4 拓展

受文[1]的启发,进一步思考抛物线与双曲线是否有文[1]性质6的类似结论,通过推导,可得到以下结论:

结论1如图4,已知抛物线C : y2= 2px(p＞0),焦点为F,准线为l.不过点F的直线与抛物线交于A、M两点,与l交于点N,则NF平分∠MFA的外角.

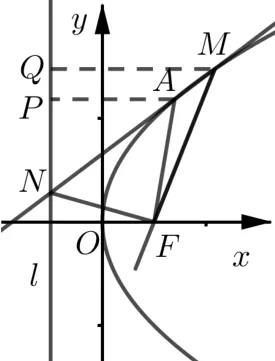
图4

①当A、M在双曲线的不同支上时, NF平分∠MFA,如图5;

图5

②当A、M在双曲线的同一支上时, NF平分∠MFA的外角,如图6.

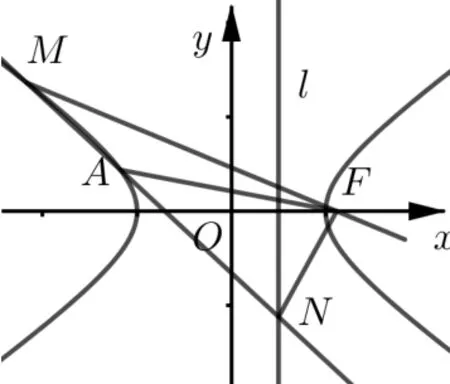
图6

结论2的证明可参照结论1的证明得到,此处不再赘述.此外,在对原题进行复盘时,出现了与原题第(2)问相反的一个问题:若点N满足∠MFD = 2∠NFD时,即NF平分∠MFA(或∠MFA的外角)时,点N是否一定会在相应的准线上?答案是肯定的,有如下结论:

结论3已知椭圆C := 1(a＞b＞0),右焦点为F,右准线为l.不过点F的直线与椭圆交于A、M两点,点N是直线AM上一点,且NF平分∠MFA的外角,则点N在右准线l上.

证明假设点N不在椭圆的右准线l上.设直线AM与右准线l交于点G,则点G与点N不重合.由上述推论可知,GF是∠MFA的外角平分线,则点N与点G均为∠MFA的外角平分线与直线AM的交点,所以点G与点N为同一点,与假设矛盾!故点N在右准线l上.

结论4已知双曲线C := 1(a＞0,b＞0),右焦点为F,右准线为l.不过点F的直线与双曲线交于A、M两点,点N是直线AM上一点:

①当A、M在双曲线不同支上,且NF平分∠MFA时,点N在右准线l上;

②当A、M在双曲线同一支上,且NF平分∠MFA的外角时,点N也在右准线l上.

结论5已知抛物线C : y2= 2px(p＞0),焦点为F,准线为l.不过F的直线与抛物线交于A、M两点,点N是直线AM上的一点,且NF平分∠MFA的外角,则点N在准线l上.

结论4与结论5的证明可参照结论3的证明,不再赘述.