基于改进的分形理论的短期电力负荷预测
徐建军,王硕昌,袁 硕,张铭桥,马 睿,潘立超
(东北石油大学 电气信息工程学院,黑龙江 大庆 163318)
0 引 言
目前应用的预测模型基本上都是通过对数据生成的曲线的特点和趋势进行分析,然后建立一定的逻辑关系,并通过逻辑关系预测后续的数据变化。常见的预测模型有灰色预测模型、ARIMA(Autoregressive Integrated Moving Average)模型、BP(Back Propagation)神经网络模型、模糊预测模型、插值预测模型、回归预测模型等,这些模型都是通过上述方法进行数据预测的。但都没考虑数据背后隐藏的局部和整体之间的重要联系和运动规律。Mandelbrot通过对自然界中的局部与整体的联系建立了一门新的学科----分形学[1]。该学科可以通过研究混乱现象和不规则构型解决上述问题。
1986年分形插值函数被提出[2],与提供适合经验数据的初等函数一样,分形插值函数可以用公式科学地表示。分形插值函数的优点是其具有一组非正维数。陶兴龙[3]利用分形维数可以表征曲面的粗糙程度的特点,通过分形维数估算修正参数以降低低频噪声。李小燕[4]通过分形插值函数选取相似日对实测日进行气象预测,再选取参考日的数据对实测日的预测数据进行回归,进一步提高了预测精度。李萌[5]通过设置调整参数和不断更新迭代初始点对分形插值函数进行修正,使其能对中长期电力负荷进行预测。佟宇[6]利用经验模态分解对原始的预测序列进行分解,再利用分型理论中的拼贴定理和分形插值函数对每个分解序列进行合理的预测。李如琦等[7]通过灰色关联法选取相似日的数据,并通过数据的特点对数据进行分段,再利用分形插值函数对分段数据进行预测和拟合。刘映等[8]通过改进垂直因子的分形插值函数对样本数据进行小波分析,通过小波分析确定分形插值点,从而有效提高了预测精度。笔者对基准日负荷数据进行重标极差法分析、二次分形插值和数据拟合,其中利用插值区间和插值点确定分形插值法中的自由参量垂直尺度因子di,通过和传统分形插值模型及BP神经网络模型对比,预测数据更加精准。文中所有负荷数据来源于美国PJM电力市场官方网站,气象数据参考美国国家气象局官网。
1 分形插值函数定理
分形插值函数需要通过给定的插值点数据,根据数据本身的规律进行插值[9],相比其他插值方法,如拉格朗提插值法、分段线性插值法、埃尔米特插值法和三次样条插值法,分形插值法不是在区间内构造函数,而是构造一个迭代函数系统(IFS:Iterative Function System),这可避免因为过拟合而导致的龙格现象(Runge Phenomenon)。该迭代函数系统(IFS)满足压缩映射定理和拼贴定理[10]。
给定一个数据集{(xi,yi)∈R2,i=0,1,2,…,N},其吸引子A是内插函数的连续函数F:[x0,xN]→R的图像。下面构造在R2上的一个IFS。
IFS{R2:ωi,i=1,2,…,N},ωi是

(1)
的仿射变换。且端点满足以下条件

(2)
式(1)对应的迭代函数系统IFS根据放射变换生成的分形插值函数(FIS)两端的端点必须满足式(2)的条件,所以每个变换都要满足

(3)

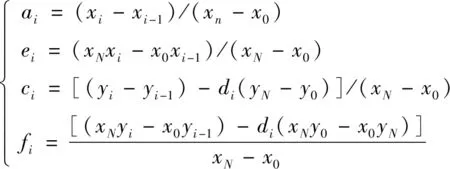
(4)
IFS的吸引子A即分形插值函数(FIS)可以通过式(4)计算得到各种参数。
2 时间序列的R/S分析
重标极差法是对时间序列的预测性进行分析,其一般步骤如下。
对时间序列{xt,t=0,1,2,…,N},设EN为时间序列的均值,X(t,N)为该序列的累积离差,R(N)为该序列的极差,S(N)为标准差。

(5)

(6)

(7)
则R(N)/S(N)为重标极差,即为
(R/S)N=cNH
(8)
其中H为Hurst指数,c为正常数,与参数N无关。时间序列中的Hurst指数H和分形维数D满足:H+D=2。
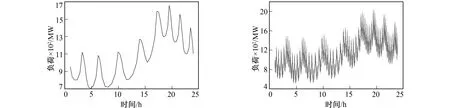
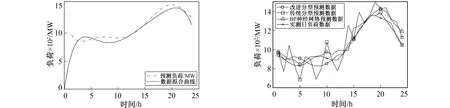
首先对基准日的时间序列进行分析,判断该时间序列是否具有分形特征,所以要对基准日的时间序列进行R/S分析。选取美国AECO(Atlantic Electric Power Company)公司的2021年9月3日作为基准日,对其进行R/S分析,结果如图1所示。通过图1中的曲线可看出,该时间序列具有明显的分形特征,且通过计算Hurst指数得到H=0.871 476,0.5 图1 美国AECO公司2021年9月3日的电力负荷数据R/S分析Fig.1 Rescale range analysis of AECO’s electrical load data for September 2021-09-03 1) 首先选取基准日[2],即对预测负荷所在的日期设为起点。选取气象数据最为接近的一天作为基准日。笔者将基准日选为2021年9月3日,即实测日的前一天。 2) 根据文献[2]选取的分形插值函数的插值点为1、4、7、11、15、18、20、22、24,选取9月3日的9个整数点作为基准值。 3) 建立基准日的电力负荷曲线的IFS。迭代函数通过步骤1)~2)建立。通过实验得出垂直尺度因子di。 4) 在实测日中进行插值,插值点分别为1、4、7、11、15、18、20、22、24,建立IFS。通过式(1)~式(4)计算ai、ei、ci、fi。 5) 预测2021年9月5日的电气负荷数据,利用确定性迭代算法获得IFS的吸引子,对9月5日的数据进行预测。 如图2所示,虚线为实际电力负荷曲线,实线为传统分形插值函数预测的电力负荷数据。从图2中可看出,传统模型预测曲线和实际负荷曲线相差较大,数据的相对误差受到传统分形模型数据量少,数据波动大的影响,导致相对误差受到插值点的影响,距离插值点越近则预测数据的相对误差越小。 图2 未改进模型预测数据和实测数据Fig.2 Comparison of predicted and measured data 计算可得MSE为7 753和MAPE为0.314 8,由此可以得出无论是均方误差还是平均绝对百分比误差的数值都不是很理想,这表明传统的分形预测模型的预测效果不佳[11]。 在分形插值函数中,垂直尺度因子di的数值直接影响分形插值曲面的粗糙程度。所以在分形插值预测中,预测的精度主要取决于垂直尺度分子di。传统分形预测模型中的垂直尺度分子是通过大量实验或对垂直尺度因子的假定得出的[2],无法满足预测模型对数据的精度需要,所以需要改进垂直尺度因子的选取方法。笔者将时间序列划分为6个子序列,经过式(9)的计算可得di=0.71。 笔者借鉴了文献[12]和文献[1]的方法,利用自身数据的特点计算垂直尺度因子,具体步骤如下。 1) 将时间序列划分长度为n+1的第N个连续的子序列。 2) 将所有序列的第1个数据和最后的子序列的最后一个数据,组成一个数据量为N+1的插值点集。 3) 过每个子序列的第1个点和最后一个点做一条直线,令d为子序列中剩余的点到直线距离的最大值。 4) 对每个子序列都进行上述操作,得到集合为{ui}。通过 (9) 计算垂直尺度因子。 5) 求出每个子序列的dq,垂直压缩因子就是所有dq的算术平均值。通过上述步骤求得笔者的垂直尺度因子di=0.71。 通过上述方法可以有效减少di的实验工作量,并且为确定分形插值函数的垂直压缩因子提供了一种更为科学的方法。 在所有分形预测模型中,都是采用一次迭代方法进行插值预测。由于迭代次数少,从而产生的数据量少,分形特征不明显,不能体现分形预测模型的优越性。图3和图4分别给出一次迭代产生的数据和二次迭代产生的数据的对比结果。 图3 一次迭代的数据 图4 二次迭代的数据Fig.3 Data for one iteration Fig.4 Data for the second iteration 通过图3和图4可看出,二次迭代生成的分形预测模型效果图更具有分形的特征且数据量更大[13],更适合进行预测。 通过二次迭代模型可得到迭代的周期为0.244 8,设置移动平均函数的向量绝对值为半个周期。设通过移动平均函数处理后的数据集为[ti-0.244 8,ti+0.244 8],其中ti为预测点对应的时间数据,通过上述方法得到的预测数据更能体现二次迭代分形插值的精准性。 通过对二次迭代生成的数据进行移动平均函数处理,并利用二次迭代生成函数的周期性对数据处理。通过Matlab软件中的随机函数对每个周期内的数据进行抽取。然后通过最小二乘法(OLS:Ordinary Least Squares)对数据进行拟合处理。 通过对处理后的数据进行数据拟合可得出 f(x)=p1x6+p2x5+p3x4+p4x3+p5x2+p6x+p7 (10) 其中p1=-0.000 475 5,p2=0.038 13,p3=-1.243,p4=20.53,p5=-171.8,p6=658.4,p7=11.4。ESSE=3.386×10-5,R2=0.987 3,误差均方和(ESSE)接近于0和拟合优度(R2)接近于1表明拟合效果很好。图5给出了拟合曲线。 因为拟合函数的局限性,导致在区间[0,2]中的数据并不理想,所以实测日的前两个数据均为基准日数据(见图6)。通过式(10)中的拟合函数计算出时间轴为整数点对应的负荷。通过文献[14-15]建立BP神经网络模型进行对比,结果如表1所示。 表1 模型数据对比Tab.1 Comparison of model data 图6是经过数据处理后的最终数据和实测数据的对比图。最终生成的数据得到的MSE为3 376.24,MPSE为0.048 16,传统模型的MSE为7 753,MPSE为0.314 8,BP神经网络模型的MSE为4 536.12,MPSE为6.083 7。通过对比3种模型可知,改进后的模型均方误差降低了近50%,平均绝对百分比误差降低近30%,对比BP神经网络模型的均方误差下降了30%,平均绝对百分比降低了5%。对比图2和图5可得出,改进的分形预测模型比传统模型更好的预测了电力负荷短期的数据,减少了运算步骤,降低了预测误差,提高了预测精度。 图5 数据拟合曲线 图6 数据对比Fig.5 Data fitting curve Fig.6 Final data and measured data 改进的分形预测模型和传统的预测模型对比具有以下优点: 1) 改进后的分形预测模型中垂直尺度因子的计算方法,降低了分形预测模型的不确定性; 2) 改进后的分形预测模型适应性很强,可以适用于多种应用情形,如天气预测、流量预测等; 3) 改进后的分形预测模型使用二次迭代比一次迭代更具有分形的特征即标度不变形和自相似性; 4) 仿真实验证明改进后的分形预测模型比传统的分形预测模型精确度更高,且均方误差和平均绝对百分比误差明显降低。 综上所述,改进后的分形预测模型在短期电力负荷预测中更具有优势。
3 传统分形预测模型
3.1 建模步骤
3.2 建模结果

4 改进的分形预测模型
4.1 分形预测模型中垂直尺度因子的改进
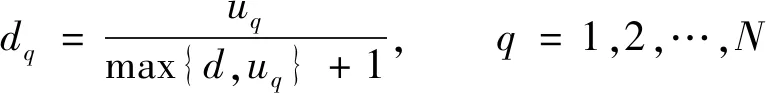
4.2 分形预测模型迭代次数改进
4.3 二次迭代产生数据的选取

5 结 论

