基于LGWO和扰动观察复合算法的MPPT研究

张铁晟,张凤武，张明毅

(1.东北石油大学 电气信息工程学院,黑龙江 大庆 163318；2.大庆油田有限责任公司 采油工程研究院，黑龙江 大庆 163453)

0 引 言

随着锂电池储能、超导电容储能技术的不断突破以及个人用户、家庭太阳能解决方案的不断完善,光伏发电的应用达到了一个全新的高度[1-3],需要更优异的配套算法对最大功率跟踪点技术进行优化。在实际生产生活中,光伏阵列的受光面积与受光强度受到乌云、高层楼房、树叶与杂物遮挡等局部阴影情况的影响,其输出功率的输出特性曲线变化为多峰值状态,传统的最大功率点跟踪方式以及一些基础的神经网络算法已不再适用。

传统MPPT(Maximum Power Point Tracking)方法如恒压法、扰动观察法[4]、电导增量法[5]已经进入深度成熟期,可解决局部最优和改善收敛速度,通常用于温度、光强恒定的条件下；而单一的高效算法如粒子群算法、灰狼算法以及布谷鸟算法等无法跳出局部最优陷阱,且收敛速度不如传统方法,具有明显的缺陷。郭昆丽等[6]提出了粒子群算法和遗传算法相结合的复合算法,并通过模糊控制方法使系统在最大功率点处稳定,但模型过于复杂需要较高的算力,收敛速度也没有明显的提升。杨丽丽[7]提出了一种改进灰狼算法,通过调整动态权重将普通灰狼算法的收敛因子由线性因子变换为非线性,解决了全局搜索与局部搜索切换混乱的问题,但收敛速度过于缓慢,仍有较大的改进空间。赵其浩[8]详细描述了局部阴影下的热斑效应和多峰值效应,但对粒子群算法的优化不足,收敛速度较慢。

针对上述问题,笔者提出了一种智能优化算法并与传统算法相结合的复合算法。首先在传统灰狼算法的基础上引入莱维飞行模块,利用贪婪策略自动淘汰适应度下降的狼,以此跳出局部最优陷阱。随着迭代次数的增加,狼群越来越集中,最大功率点跟踪方法切换为扰动观察法,利用扰动观察法收敛的快速性迅速确定最大功率跟踪点。这种复合算法跳出了局部阴影情况下产生的局部最优陷阱,提高了系统的准确性；并利用扰动观察法提升整个系统收敛的快速性。此方法可以在快速性和准确性两方面优化最大功率点跟踪技术,减少由于局部阴影等因素对光伏发电输出功率的不良影响。

1 光伏板阵列输出特性

1.1 光伏板阵列仿真模型

图1是利用Matlab Simulink模块库搭建的光伏板阵列在不同辐照度下的仿真模型。为防止局部温度过高,保证光伏板稳定运行,每块光伏板电池均反并联一个二极管,不同光伏板阵列通过串联方式进行连接。笔者分别设置1 000 W/m2、800 W/m2、400 W/m23种不同辐照度模拟局部阴影的情况,实验温度设置为室外常温25 ℃。表1给出了局部阴影模拟数据以及光伏板阵列的参数。

图1 光伏板阵列局部阴影仿真模型Fig.1 Local shadow simulation model of photovoltaic panel array

表1 仿真模型各类参数设置Tab.1 Various parameter settings of simulation model

1.2 光伏板阵列输出特性曲线

从图1中的光伏板阵列仿真模型可得到光伏板阵列的输出电压P、电流I和功率U,得到的U-I以及U-P曲线(即光伏板阵列的输出特性曲线)如图2所示。由于光伏板阵列的输出功率受外界环境变化的影响,如室外气温、太阳光照辐射强度等,所以光伏板阵列的U-P特性为一条非线性曲线。从图2b可看出,U-P曲线出现了3个局部峰值,其中仅有一个为最大功率输出点,其余两个局部峰值为局部最优陷阱。由图1的最大功率输出计量器可以看出最大输出功率为5 761 W,而两个局部最优的输出功率值仅为238.7 W和24.14 W,仅用传统方法如扰动观察法或单一智能算法如粒子群、灰狼算法等,无法跳出局部最优陷阱,一旦陷入非最大值处的局部最优峰值中,光伏板阵列不能在最大功率点处工作,会造成大量能量损失,大大降低光伏发电的效率。

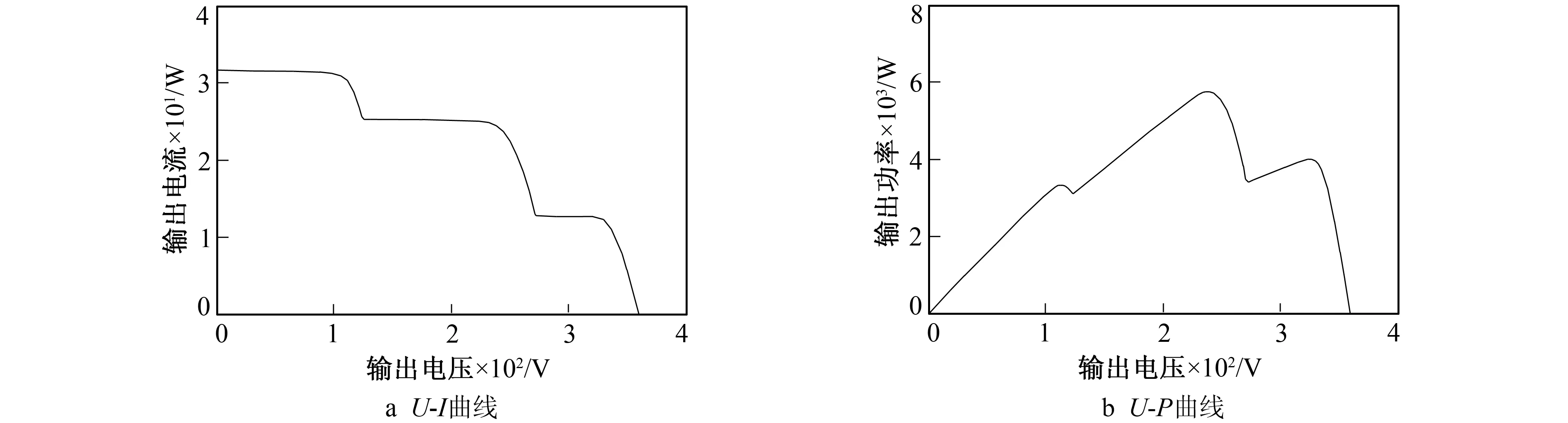
图2 局部阴影下光伏阵列输出特性Fig.2 Output characteristics of photovoltaic array under local shadow

2 莱维灰狼与扰动观察复合算法基本原理

2.1 基本灰狼算法

灰狼是犬科动物的后代,群居的灰狼处于食物链的顶端。灰狼算法是由Atici等[9]提出的单一优化算法,其灵感来源于灰狼捕猎过程中明确的层级分工策略。

狼群算法中一般有5～12匹狼,可根据求解的具体需要进行调整。捕猎中的狼分为4个层级,分别为α狼、β狼、δ狼和ω狼。其中α狼代表最理想的解决方案,第2和第3的最佳解决方案分别为β狼和δ狼,其余候选解假设为ω狼,跟随前3匹狼[10]。图3给出了灰狼算法的3个主要步骤,即跟踪、包围和攻击猎物。其中包围行为可通过

图3 灰狼集群捕猎过程Fig.3 Wolves hunting in packs

D=|CXP(t)-X(t)|

(1)

X(t+1)=XP(t)-AD

(2)

进行建模。其中t表示当前迭代,D、A和C表示系数向量,XP表示猎物的位置向量,X表示灰狼的位置向量。向量A和C由

Ab=2ar1-a

(3)

C=2r2

(4)

计算得到。在迭代过程中,分量α、β、δ均从2线性减小到0,r1、r2均为[0,1]中的随机向量。在狩猎过程中灰狼位置的更新由

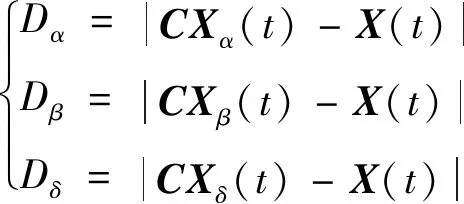
(5)

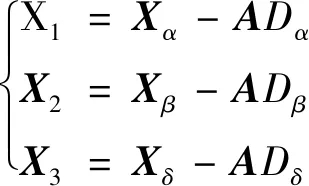
(6)

(7)

表示。其中D表示狼与猎物的距离[11]；式(6)和式(7)表示ω狼朝向3只头狼靠近的方向和步长。

2.2 嵌入莱维飞行模块的灰狼优化算法

莱维飞行是一种概率分布情形,其采取一种随机改变前进方向和大范围变化运动步长的搜索方式进行求解。因此在嵌入莱维飞行模块后,灰狼算法便可以跳出局部最优陷阱[12],更容易获得最优解。

在基础灰狼算法中,头狼α代表最优解,因此是狼群中最重要的阶层。在灰狼算法迭代几轮后,狼群中所有狼都要向最优解α狼靠拢,这导致了狼群阶层多样性的丧失,容易陷入局部最优陷阱。在引入莱维飞行模块后,新一代头狼α的位置计算公式如下

Xα(t+1)=Xα(t)-a⊕L(β)

(8)

其中X(t)表示头狼α的即时位置,a表示改变头狼α下一个位置的随机系数,如下

a=random(size(αposition))

(9)

L(β)表示由式(9)确定的头狼α随机搜索路径。

(10)

其中β的取值范围在1～3之间；Xαbest代表α狼的最佳位置；μ服从期望为0、标准差为σμ的正态分布,σμ的取值由

(11)

得到,υ服从标准正态分布[13]。嵌入莱维飞行模块后的灰狼优化算法求解过程如图4所示。

图4 嵌入莱维模块的灰狼优化算法流程Fig.4 Flow chart of gray wolf optimization algorithm embedded in Levy module

2.3 莱维灰狼与扰动观察法复合算法的基本原理

扰动观察法是一种传统的最大功率跟踪方法,与恒压法和电导增量法并称为“MPPT三大方法”。其在实际生产过程中通过调整参考电压对最大功率点进行实时跟踪,比较添加扰动前后的输出功率确定最大输出功率,本质是一个自动寻优过程。但其容易陷入局部最优且当步长设置不当时容易引起震荡。

由于扰动观察法具有快速收敛的优点,笔者将扰动观察法与莱维灰狼算法相结合。在莱维灰狼法稳定在最大功率点附近时,将系统的操作权由α狼转交给扰动观察法,算法切换判据如下

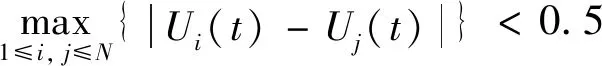
(12)

其中Ui(t)与Uj(t)表示同一次迭代中,头狼所对应的电压值。

利用扰动观察法使系统迅速收敛,从而寻得最大功率点。如果辐照度继续发生变化,则重启智能算法如下

(13)

其中P和P1分别表示扰动观察法当前和前一次采样功率值。

整个复合算法具体操作流程如下:

1) 初始化狼群位置与算法参数；

2) 计算每只狼所在位置的适应度,采用贪婪算法淘汰低适应度的狼；

3) 引入莱维飞行模块进行全局搜索,更新所有狼的位置；

4) 判断是否逼近全局最优解；

5) 切换为扰动观察法快速收敛找到最优解。

3 仿真及实验结果

根据灰狼优化与扰动观察复合算法的求解流程,搭建如图5所示的Simulink仿真模型。根据反复测试与修正,设定引入莱维飞行模块的灰狼优化算法迭代次数为6次,在保证寻得全局最优的基础上尽可能减少计算量、缩短求解时长,在莱维灰狼算法逼近最大功率点附近后立即切换为扰动观察法使其快速收敛,并稳定在最大功率点处。

图5 复合算法仿真模型Fig.5 Compound algorithm simulation model

运行图5中仿真模型,由于前期灰狼优化算法占空比延时设置为0.01 s,初始狼共7只,故将初始狼群中每个个体的位置均匀分布,设为0.1～0.7。迭代1次后,由于算法中加入了贪婪策略,会自动淘汰更新位置后适应度下降的狼,由于每只狼的初始位置不同,部分狼在第1次迭代前就已在最优解附近,因此会出现迭代之后相较初始位置并没有发生变化的情况,如表2所示。

表2 狼群初始分布与首轮淘汰表Tab.2 Wolves initial distribution and first round elimination table

随着迭代次数的增加,狼群也会越来越集中,各狼的相对距离也会越来越近,莱维步长的增量也会越来越小,最后狼群会收敛于最大功率点附近,如表3所示。从表3中可看出,在迭代6次后,引入莱维飞行模块的灰狼优化算法成功逼近到了最大功率点附近。

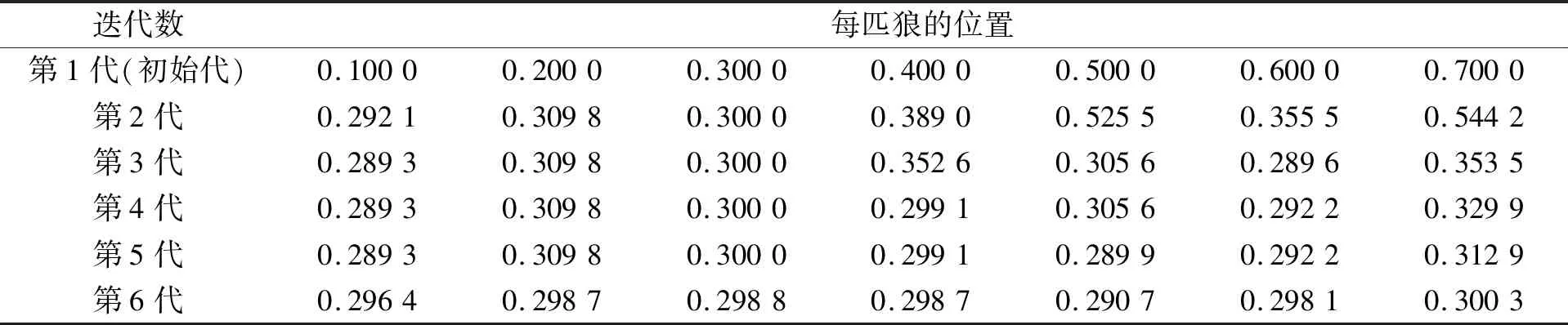
表3 灰狼优化算法寻优数据表Tab.3 Grey wolf optimization algorithm to optimize the data table

此时仿真会切换到扰动观察法,在最大功率点附近进行局部寻优(见图6),采用扰动观察法时不再有占空比延时,占空比开始连续变化。寻优的起点以头狼α的位置为参考点,由于头狼α的位置已经在最大功率点附近,此时采用扰动观察法进行寻优可快速定位最大功率点并拥有较高的精度,由于占空比变化而造成的功率波动也有所下降。

图6 灰狼与扰动观察切换过程Fig.6 Gray wolves and disturbance observation switch process

综上,笔者所提出的优化算法在前期经历6次迭代后靠拢至全局最大功率点附近,并在0.21 s附近切换为扰动观察法进行最大功率点跟踪,整个过程不仅跳出了局部最优陷阱而且能使光伏板阵列快速、稳定地工作在最大功率点,复合算法的仿真波形如图7所示。

图7 复合算法仿真波形Fig.7 Simulation waveform of compound algorithm

为验证笔者复合算法的有效性,将复合算法与传统的扰动观察法以及普通的灰狼算法进行比较。扰动观察法在早期的光伏发电领域中已有广泛的应用,其寻优速度较快但输出电压和输出电流的纹波较大,稳定性较差[14],从图8中可看出,在单峰值条件下,扰动观察法的寻优时间小于0.05 s,具有良好的快速收敛能力,但其会在最大功率点附近震荡,无法稳定在最大功率点处,造成较大的功率波动。

图8 扰动观察法单峰值仿真波形 图9 普通灰狼算法仿真波形Fig.8 Peak simulation waveform of perturbation observation method Fig.9 Simulation waveform of common gray wolf algorithm

普通灰狼算法十分复杂,需要迭代15次左右才能较为准确地追踪到最大功率点,寻优时间长达1.5 s,如图9所示。在局部遮荫等复杂条件下,还有陷入局部最优陷阱的风险。笔者提出的复合算法包含莱维灰狼优化和扰动观察法两部分。该算法不仅依靠莱维飞行模块跳出了局部最优陷阱,追踪到的最大功率Pmax为5 761 W,系统的实际最大功率为5 762.218 W,跟踪精度高达99.98%；还利用前期算法中引入的贪婪策略和后期扰动观察法迅速收敛的特性,大大提升了整体寻优速度,把寻优时间控制在0.25 s以内,相较于传统灰狼算法求解速度提升了83.3%左右。

4 结 论

笔者针对光伏发电最大功率点跟踪问题,提出了一种莱维灰狼优化算法和扰动观察法相结合的新型复合控制算法,并利用Matlab Simulink仿真验证了复合算法的可行性和优越性,通过对实验结果的分析,得到如下结论:

1) 提出的复合控制方法将莱维灰狼优化算法的全局搜索能力与扰动观察法的局部搜索能力相结合,提高了最大功率点跟踪的精度与速度；

2) 通过准确的跟踪方法切换,使扰动观察法在最大功率跟踪点附近直接局部寻优,可最大程度抑制扰动观察法在寻优过程中的电压和功率波动；

3) 在莱维灰狼优化算法中加入贪婪策略,在保证全局最优搜索的基础上极大的加快了智能优化算法的跟踪速度。