优化的GA算法在大型配电网络重构中的应用

姜建国,郭晓丽,陈 鹏,佟麟阁,万成德

(东北石油大学 电气信息工程学院,黑龙江 大庆 163318)

0 引 言

配电网重构[1]是实现主动配电网的重要优化工具,不需要额外添加操作设备,对变压器电容等进行投切操作,仅通过改变部分开关的连接状态,可减少电力损耗,平衡过载,提高供电可靠性[2]。

重构问题是非线性、多目标的最优化问题[3],目前应用于最优化问题求解的算法主要分为精确算法和近似算法两类[4]。采用精确算法求大型配电网最优结构耗费时间过长,因此主要使用近似算法的元启发式算法求解,这类算法兼具随机算法的随机特性与局部搜索算法的搜索速度,目前已经有很多研究报道。张剑等[3]将配电网络的拓扑结构等效成树状图,对每个分支上的开关进行十进制编码,提高搜索效率,满足了“开环运行”的要求。胡雯等[5]利用自适应遗传算法基于开关是否形成环路决定是否参与编码进行重构以加快计算速度,但对初始种群规模需要进行限制,应用于大型系统易蜕变成枚举法。Dos等[6]采用改进和声算法加快了在配电网拓扑搜索过程速度。Huang等[7]用小数编码方式代替二进制编码,依据概率循环解码,引入图论知识化简拓扑结构,采用粒子群算法求解最优结构。关海鹏等[8]以馈线为单位采集信息,利用单相模型等效替代三相模型,采用前推回代法计算潮流并与最小生成树相结合,采用Kruskal算法进行优化重构,其算法属于贪心算法,实际操作有待考证。

上述智能算法的研究主要面向中小型网络,对大型网络的重构研究较少。而遗传算法是基于生物进化原则[9],模拟优胜劣汰的选择过程筛选问题最优的方法,它将寻优解进程与种群进化得到适应度最佳的个体相类比,并行求解和全局寻优能力强[10]。笔者对传统的GA(Genetic Algorithm)算法的每个环节进行优化,引入精英策略,保留优良个体,避免其在求解过程中丢失,在变异环节引入局部变异,提高种群多样性,改善早熟,将其应用于大型配电网络,可有效降低线损。

1 重构数学模型

1.1 网络模型

配电网通常设计为闭环,但运行过程中要保持辐射状拓扑结构,即联络开关与分段开关不能同时全部闭合。为避免形成环路影响配电网通电状态,引入图论知识对配电网拓扑结构进行化简[11]。以连接负荷的线路为边L,所有的负荷节点为顶点V组成无向图A,记为A=(L,V),L(n),V(n)为边和顶点数目。以图1为例,L(n)=11,V(n)=10,实线L1-2、L2-3、L3-4、L2-9、L2-5、L3-6、L6-7、L8-9、L9-10为分段开关,L4-8、L5-6为联络开关。采用深度优先遍历法搜索路径,记录从起点出发的所有符合要求的路径。图1中,当L2-9、L9-8、L8-4、L3-4、L2-3均处于闭合时,形成环路。若形成环路则打开某个开关,判断其是否保证正常运行条件,若不能保证则重新选择断开的开关,直到满足条件[12]。

图1 简化网络图例图Fig.1 Simplified network legend diagram

访问路径如表1所示。

表1 图1访问路径Tab.1 Access path of figure 1

1.2 约束条件

1) 电压约束

Vmin≤V≤Vmax

(1)

2) 支路容量约束

S≤Smax

(2)

3) 网络拓扑结构约束：运行网络需为辐射状,无孤岛[13]。

4) 潮流方程g(x)成立,即

(3)

(4)

1.3 目标函数

配电网重构的主要目的是提高经济效益,减少不必要的损耗。为简化计算,在引入支路关联系数ri,以线损最小为目标

(5)

其中g(x)=0,Vmin≤V≤Vmax,Si≤Simax。nb为支路总数,ri为支路关联系数,当该支路不构成孤岛以及环路运行,ri=1；否则ri=0。F为系统总功率损耗,g(x)为潮流方程,Vmin,Vmax分别为支路各点电压的上下限,Simax为支路传输功率最大值。

为放宽不等式约束条件,以获得更大的解空间,引入对电压及容量的惩罚函数,故最终目标函数f可表示为

(6)

其中fv为违反电压幅值的惩罚函数,fS为违反容量限制的惩罚函数,k1、k2为惩罚系数。

1.4 最优负荷转移模型

在配电网中,通常联络开关闭合使其变成环状结构,为保持辐射状结构,闭合联络开关必然打开一个分段开关。为方便在后续算法中的编码操作,简化两种开关的交换,建立最优负荷转移模型[14]如图2所示。

图2 联络开关连接的环网Fig.2 Simplified network legend diagram

该环网左右侧分支集M,N定义如下

M={L1,L2,…,LM},N={LM,LM+1,…,LN}

两侧支路潮流可近似为

(7)

(8)

其中Pi,Qi为i节点处的潮流；Pj,Qj为下游节点功率。

设由联络开关关联的支路电阻为rk,当Ui=1 p.u.时,可近似计算出环网线损

(9)

与左侧交换开关后,新网络的线损为

(10)

寻找最佳转移负荷即找到Pk+jQk的最小值,令

(11)

解方程得

(12)

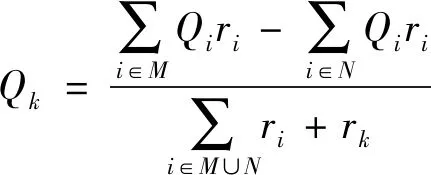
(13)

依据找到的最佳转移负荷Pk+jQk确定功率损耗降低的顺序,步骤如下。

Step 1 找到编号为1的具有降损指令的交换开关。

1)如果Pk+jQk>0,最佳转移负荷Pk+jQk实际上是从集合M传递到集合N。集合M中功率流最接近Pk+jQk的线路是匹配线路。与该段线路和联络开关相联的开关是具有1号降损指令的交换开关。

2) 如果Pk+jQk<0,最佳转移负荷Pk+jQk是从集合N转移到集合M的。集合M中功率流最接近Pk+jQk的线路是匹配线路。同理与该段线路和联络开关相联的开关是具有1号降损指令的交换开关。

Step 2 找到编号为2具有降损指令的交换开关。

2号降损指令的分段开关位于1号的左侧或右侧相邻开关。

Step 3 同理,找到其他具有降损指令的交换开关。

编号为3的分段开关必须是1号和2号开关的左侧或右侧相邻公共支路中的开关。以相同的方式确定其他使功率损耗降低的交换开关。

1.5 大型网络的脆弱性

电力系统网络是复杂网络中的人造物理网络[15],相较于结构简单、潮流走向较单一的小型配电网,大型网络的拓扑结构中具有节点的度分布严重不均匀的特点,度越高越为关键,断开度较高的节点对配电网的冲击程度更严重,在重构过程中选用大型网络验证具有更高的价值。

2 优化遗传算法

对配电网中所有的路径按照要求搜索完毕,并对拓扑结构进行简化潮流计算结束后,利用遗传算法基因适应自然的原理,由上代最佳信息产生并创造新搜索点。在重构中,开关的“开”或 “闭”对应“编码”,而调整后的总线损最小对应“适应度函数”。目前地区或城市规模扩大,配电网规模结构随之扩大并变得复杂,但对重构的研究仍集中于中小型规模的网络,故采用笔者优化的遗传算法求解大规模网络重构问题。

2.1 编 码

对需要求解优化的变量进行编码,使其能在算法中运算。编码方式决定了求解空间规模和算法运行速度。经对比,采用文献[16]中不重复环路的十进制编码方式,在算法处理中再将十进制转为二进制,图1中编码路径及个体如表2所示。

表2 编码路径及个体Tab.2 Coding path and individual

2.2 初始种群

以候选解的个数为依据随机产生初始种群,以图1网络为例,H1环路候选解有4个,染色体个数可取1,基因个数有24个。

2.3 评 价

求解最小值问题,评价函数表达为

(14)

2.4 基因操作

基因操作包含3部分：繁殖、交叉和变异。针对遗传算法容易陷入局部最优解[17-19]问题,对传统算法中的基因操作进行优化,增添解空间的个体的多样性,快速得到评价函数值最大的解[20]。

1) 繁殖。繁殖即选择过程,是物竞天择,适者生存的关键操作。在选择过程中使用锦标赛方法,采用放回抽样,挑选适应度值最优的一个,遗传给后代,并引入精英概念,使父代种群中表现优良的性状能传递给下一代,缩短迭代时间,高效寻优。

2) 交叉。由于大型网络开关较多,算法使用单亲遗传交叉收敛速度比其他交叉规则收敛快。从上级种群选取一个父代,由该父代自身基因单点交换创造子代,以两点交叉为例,从A交叉产生A′,交叉过程如表3所示。

表3 单亲遗传交叉方式例表Tab.3 Table of single parent genetic crossover patterns

3) 变异。在产生新个体过程中染色体中某两位发生变异,并在此基础上引入局部变异,以及其微小的概率随机在产生的子代中再变异一次,以解决早熟收敛问题。由B到B′变异过程如表4所示。

表4 变异过程Tab.4 Mutation process

2.5 算法流程图

基于优化遗传算法的大型配电网重构流程如图3所示。

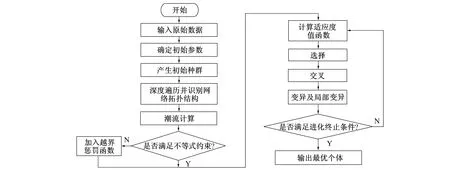
图3 重构算法流程Fig.3 Flow chart of reconfiguration algorithm

3 算例分析

以IEEE118节点配电系统为测试系统,拥有118个分段开关,15个联络开关,节点1为电源节点,拓扑结构如图4所示,对网络结构的遍历图如图5所示,各支路线损如表5所示。总负载功率为P=22 709.7 kW,Q=17 041.1 kVar。

图4 118节点拓扑图 图5 118节点遍历图Fig.4 IEEE 118 topological map Fig.5 IEEE118 ergodic graph

笔者所述优化算法的参数如下：初始种群数目为40,染色体长度为15,锦标赛法选择系数为0.9,交叉概率为0.9,交叉点数为6,变异概率为0.01,局部变异概率为0.000 1,迭代次数为100。

图6为采用优化遗传算法进行重构后的配电网拓扑图,重构动作的开关及线损如表5所示,重构后网络损耗降低了约60%,证明将该优化算法用于大型配电网重构可有效降低线损。

图6 优化后的网络拓扑图Fig.6 Optimized network topology

表5 动作的开关和线损Tab.5 Switch and power loss

将笔者算法与应用蒙特卡洛算法重构的线损及节点电压相比较,如图7、图8所示,充分说明笔者算法更能快速地降低线损,寻优效率高,重构后电压高的优势。

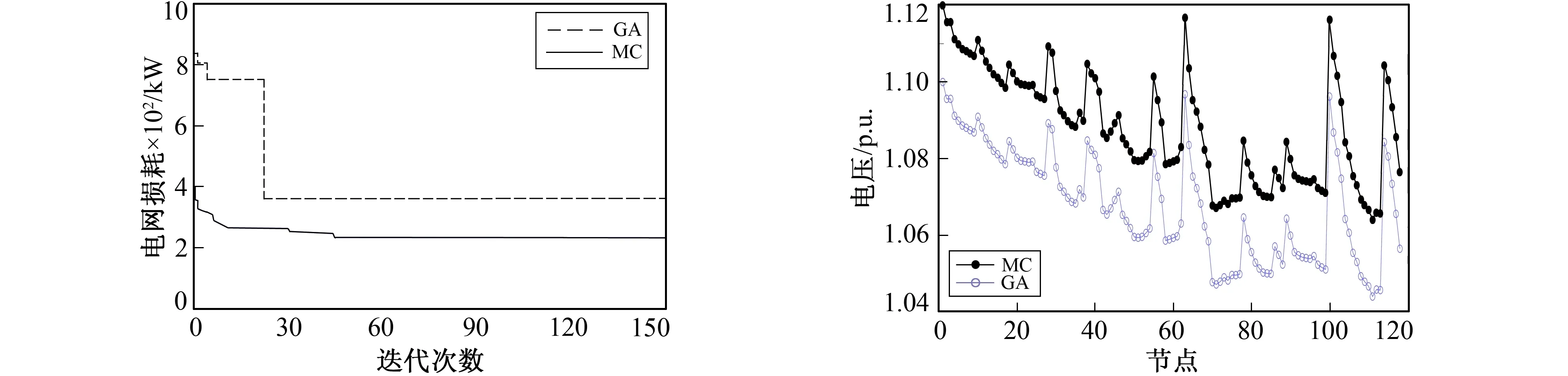
图7 蒙特卡洛算法与优化遗传算法重构后的线损比较图 图8 蒙特卡洛算法与优化遗传算法重构后的电压比较图Fig.7 Comparison of network loss after reconfiguration of MC and GA Fig.8 Comparison of voltage after reconfiguration of MC and GA

4 结 语

笔者提出了一种优化的用于大型配电网重构的遗传算法,简化配电网的拓扑结构,采用深度遍历方法快速准确遍历路径,引入负荷转移模型,优化了算法寻找需要动作的开关顺序,改进了目标函数,有效避开不可行解,同时在基因操作环节中引入局部变异概念,使可行解多样化。笔者算法及模型在IEEE118节点系统进行测试,结果表明在提高搜索速度的同时可明显降低线损,减少节点电压降落水平。