一种新的生成树组随机求取算法

董张卓，罗 辉，齐 洋

(1.西安石油大学 电子工程学院，陕西 西安 710065； 2.西安科技大学 电气与控制工程学院，陕西 西安 710054)

引 言

在电力[1-2]、通信、管网、公路网、医疗[3-4]等实际问题以及优化设计中，通过一定方法将问题等效成一个平面图，用不包括环路能达到每一个节点的连通图，即对图的生成树的求解[5]，得到工程问题的可行解是一个典型的方法。

此类问题均可归为针对无向图和有向图求生成树的问题，求解该类问题目前有数种方法。第一种方法是BST算法[6]，用子树集的概念从空集出发，按节点的编号顺序，逐一向集合中添加至少在有向图G的一颗以r为根的生成树上的支路，直至得到该图的某个生成树为止。第二种方法是在G-M算法[7]的基础上，从根出发，找到以r为根的图G的每棵生成树中都存在的支路e，确定搜索时间和搜索空间后，采用基于深度优先搜索方法[8]得到生成树，提高方法的运行效率。第三种方法是给有向图赋权后以权值为参考生成最小生成树[1]。

以上算法仅适用于求解节点数和支路数较少的图的生成树，且随着图的规模增大，求解效率逐渐变低，同时，这些算法一般应用于求解一棵生成树，并不适合于求解一组生成树。为此，本文提出一种基于简化图的生成树算法。为了减小问题的规模，首先定义简化规则将图进行简化，在简化图的基础上，提出一种随机生成树组求解算法得到生成树的集合，即建立一种通过对原图和对应的树图通过轮盘赌的方式随机选择支路进行迁移的算法，生成连通图。通过多次应用生成树计算方法，生成不同的树，得到生成树组。

1 生成树计算模型

定义1 大规模复杂连通图GF∷=，其中BF为支路集合，NF为节点集合。

计算连通图GF的生成树组时，为了减小生成树的计算量，首先对不涉及到生成树的支路图部分进行简化得到简化图，针对简化图G计算得到的生成树组加上简化的部分即为原连通图的树组。不失一般性，在图的简化过程中，只给出简化方法；计算过程中，只针对简化图进行计算。

1.1 复杂连通图的简化

为了减小复杂图的规模，对其进行简化得到简化图。将图中不涉及环路的辐射支路、节点以及直接串联的支路进行化简。为此给出以下概念的定义：

定义2 辐射通路，不包含在任何环路中的通路称为辐射通路；

定义3 互斥支路，由度为2的节点连接的两条支路称为互斥支路。

定义4 互斥支路集，集合{bi|i=1,2，…，nb}，若bi和bi+1互斥，且bi+1和bi+2互斥，i=1,2，…，nb-2，称集合为互斥支路集

辐射通路不存在于任何环路中，所以不参与生成树的生成过程。同时由定义3知，互斥支路集在求取开环图时最多只需打开一条支路。因此，将互斥支路进行合并。故根据图论的相关概念和上述定义，给出复杂图的简化规则：①删除复杂图中所有辐射通路；②将复杂图中的互斥支路集等效为一条支路。

1.2 简化图生成树算法

1.2.1 过渡图的定义

定义5 简化图，图G为图GF经过简化后得到的图：

G∷=。

(1)

其中：B为图中的支路集合，B={bi|i=1,2，…，nb}，bi为图中支路的编号，nb为图中支路个数，N为图中的节点集合，N={ni|i=1,2，…，nn}，ni为图中节点的编号，nn为图中节点个数。

定义6 生成树图GT，图G的生成树定义为含有图G所有节点连通的无环路的一个子图：

GT∷=。

(2)

其中：BT为图中的支路集合，BT={bTi|i=1,2，…，nTb}，bTi为支路的编号，nTb为生成树中支路个数；NT为图中的节点集合NT={nTi|i=1,2，…，nTn}，nTi为节点的编号，nTn为生成树节点个数。

定义7 过渡图GB，生成树图过程中的一个临时图，初始时由简化图G生成，完全等值于简化图G，按照算法生成树的过程中，逐渐迁出一些支路，完成生成树计算后，图GB中为图G的连支，

GB∷=。

(3)

其中：BB为图中的支路集合；NB为图中的节点集合。

1.2.2 生成树组树支未选中概率

为保证生成树组计算过程中树的多样性，以及考虑生成树组在后期计算过程中效率降低问题，在第一次计算完成得到第一个生成树后，对化简图G以及过渡图GB的支路加入选中作为树支的计数值iNoc_T，即某一支路在一棵生成树中出现一次，该支路的计数值iNoc_T+1，当计算完成的树的总数为iTn_T时，某条支路作为树支的概率为

(4)

则支路未选中作为树支的概率

Pn_t=1-Pt。

(5)

1.2.3 随机生成树计算原理

一颗随机生成树的计算过程分为3个部分，初始化部分，支路迁移循环部分、线索支路搜索部分。

初始化部分：过渡图GB的生成、生成树图GT初始化以及在生成树计算过程中记录当前支路和当前处理节点的变量的定义。过渡图GB初始化为原图G，生成树图GT的支路集合和节点集合为空集。在图GB中用轮盘赌算法随机选择的一条支路bk，取支路bk关联的节点j。在图GB中移除bk,图GT中添加支路bk及支路两端的节点i,j，即图GT的BT={bk},NT={i,j},当前节点C_n=j。

支路迁移循环部分：在图GB以当前节点C_n为线索，得到其关联的支路集Bsel={bj|j=1,2,…,nb}，用轮盘赌算法随机从支路集Bsel中选中一条支路bk，得到其对端节点j,如果j∉NT,C_b=bk，C_n=j,图GB中移除C_b=bk,图GT中添加支路C_b、节点C_j，重开始支路迁移部分；否则，转执行线索支路搜索。

线索支路搜索部分：遍历GB中支路，取支路bk的对应节点i,j，如果i∉NT∨j∉NT成立，得到C_b=bk，C_n=i∉NTi:j,转支路迁移循环,否则，计算完成。

在每次计算得到新的生成树后，更新图G中支路计数值iNoc_T以及生成树数目iTn_T，并在下一次生成树的计算过程中以Pn_t为基准采用轮盘赌的方式对当前节点的待选支路集中的支路进行选择。

1.2.4 随机生成树组的形成

为了得到一组完全的生成树，需多次应用上述随机生成树算法形成生成树组。将得到的生成树存入生成树组时，将支路按序号从小到大排序，逐一对已有生成树方案中的支路进行对比，判别该生成树是否与已有的方案相同，若相同，移除该方案并重新生成新的生成树；若不同，则存入生成树组。

2 随机生成树算法实现

以图1为例，包含28个节点和32条支路，对随机生成树计算过程进行说明，给出随机生成树的计算方法。

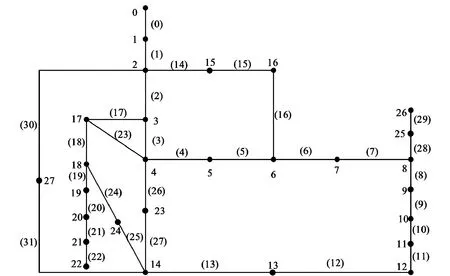
图1 复杂无向连通图Fig.1 Complex undirected connected graph

2.1 简化过程

按照上述简化规则对该图进行简化得对应的简化图图2。

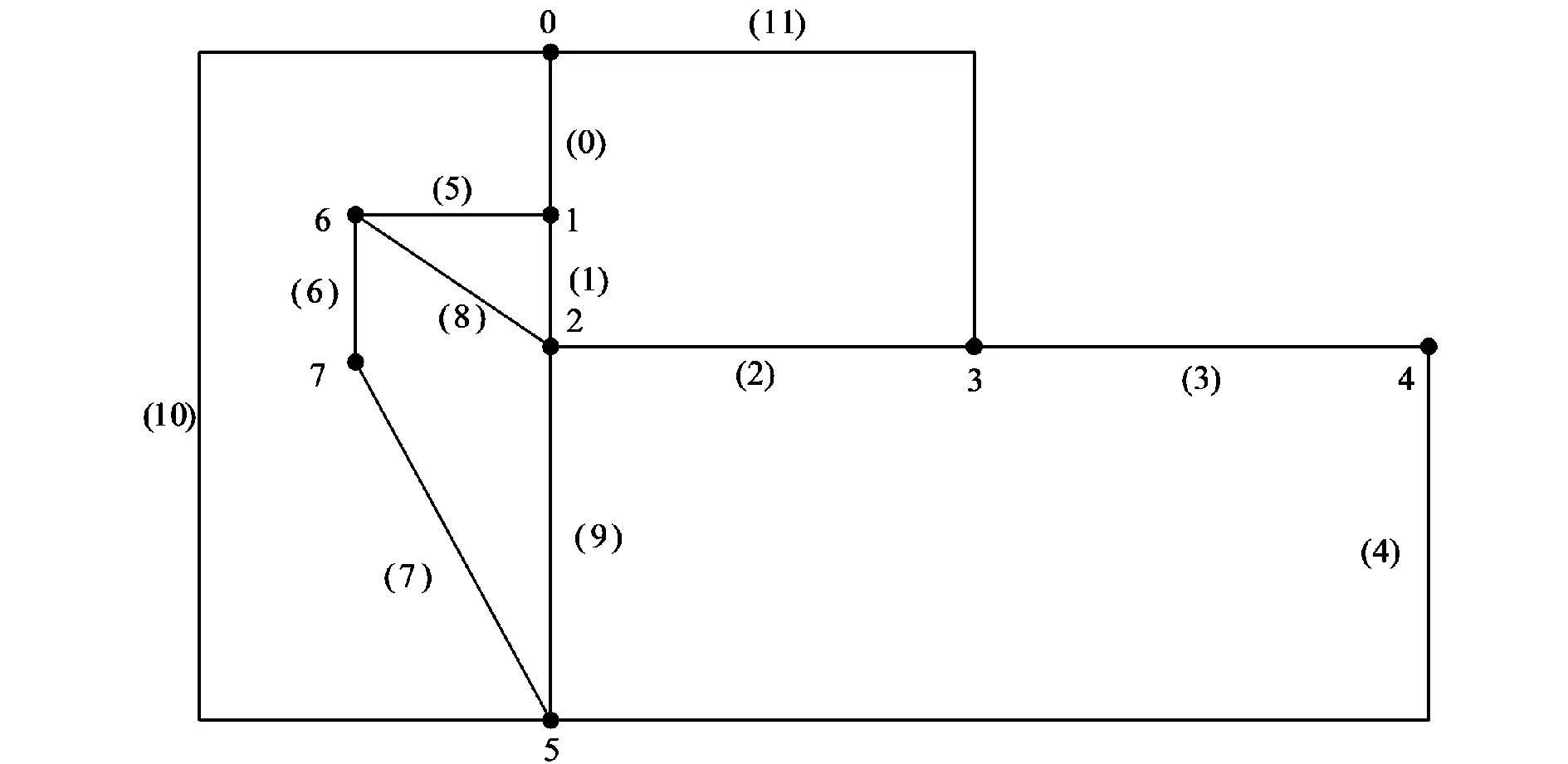
图2 复杂图对应的简化图Fig.2 Simplified graph corresponding to complex graph

2.2 随机生成树计算过程

以图2所示化简图为例，进行生成树的计算过程说明，过程如图3所示。

图3 生成树生成过程图Fig.3 Generation process of spanning tree

2.3 算法过程中节点与支路的数据表示

根据图的特点，使用关系表的形式描述节点和支路的连接关系，见表1。

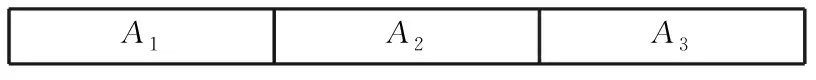
表1 节点与支路的连接关系表Tab.1 Connection relationship between nodes and branches

数组A分3个域：A1域为节点编号，A2域、A3域分别为节点度和节点连接的支路的编号序列。

将等效后的支路与等效前的支路进行对应，对应关系见表2。

表2 支路与互斥支路集的对应关系表Tab.2 Correspondence between branch and mutually exclusive branch set

B的元素分2个域：B1域为简化图中支路编号，B2域为复杂图中对应的互斥支路组中的支路编号。表3即为复杂图1中互斥支路集与简化图2中支路的对应关系表。

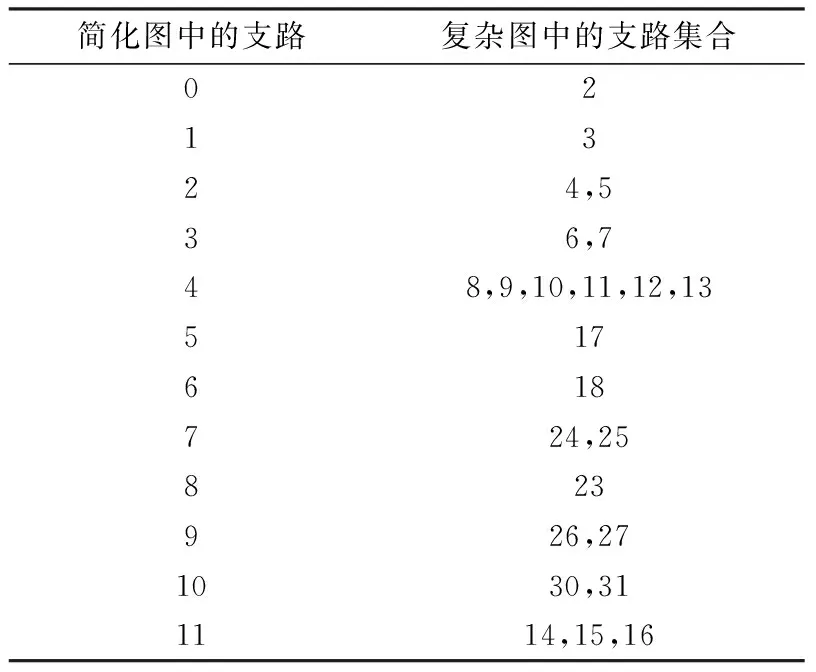
表3 支路与互斥支路组对应表Tab.3 Correspondence between branches and mutually exclusive branch sets

在图GB中的支路属性中，加入一个选中为树支的计数器，用来记录支路选中为树支的次数。生成树组的存贮采用结构见表4。

表4 生成树的支路对应关系表Tab.4 Correspondence among branches of spanning tree

数组C分3个域：C1域为树的编号，C2域、C3域分别为支路的编号和树支的编号序列。

2.4 随机生成树组计算过程

随机生成树组计算步骤及流程如图4所示。

步骤1：初始化图G中各支路的未选中计数值iNoc_T=0，树个数iTn_T=0。

步骤2：初始化建立GT

(1)建立支路和节点集合BT={}，NT={}；建立当前支路变量C_b,以及当前节点变量C_n。

(2)随机选取图GB中支路BB中的一条支路bk，得到支路两端的节点i,j，图GT中添加支路bk，及支路两端的节点，即图GT的BT={bk},NT={i,j}。

(3)从GB中将支路bk移除，BB=BB-{bk}。

(4)C_b=bk，C_n=j。

步骤3：对当前节点、以及当前支路的处理。

(1)从图GB中，得到当前节点C_n连接的支

路集合Bsel,如果Bsel=Ø，转(6)。

(2)基于Pn_t采用轮盘赌的方式从Bsel中选择一条支路bk，(a)得到bk对应另一侧节点j,判断节点j∉NT，即不为GT的节点，转(3)。否则Bsel=Bsel-{bk}并随机选取一支路bk，为空转(6)，否则转(a)。

(3)C_b=bk，C_n=j。

(4)GT中加入bk，即BT=BT+bk}，NT=NT+j}。

(5)GB中移除支路bk，即BB=B-{bk}，转(1)。

(6)遍历GB中支路，取支路bk节点i,j，如果i∉NT∨j∉NT成立，得到C_b=bk，C_n=i∉NTi:j,转(1),否则，转步骤3。

步骤4：输出GB,GT中支路集合BB、BT。

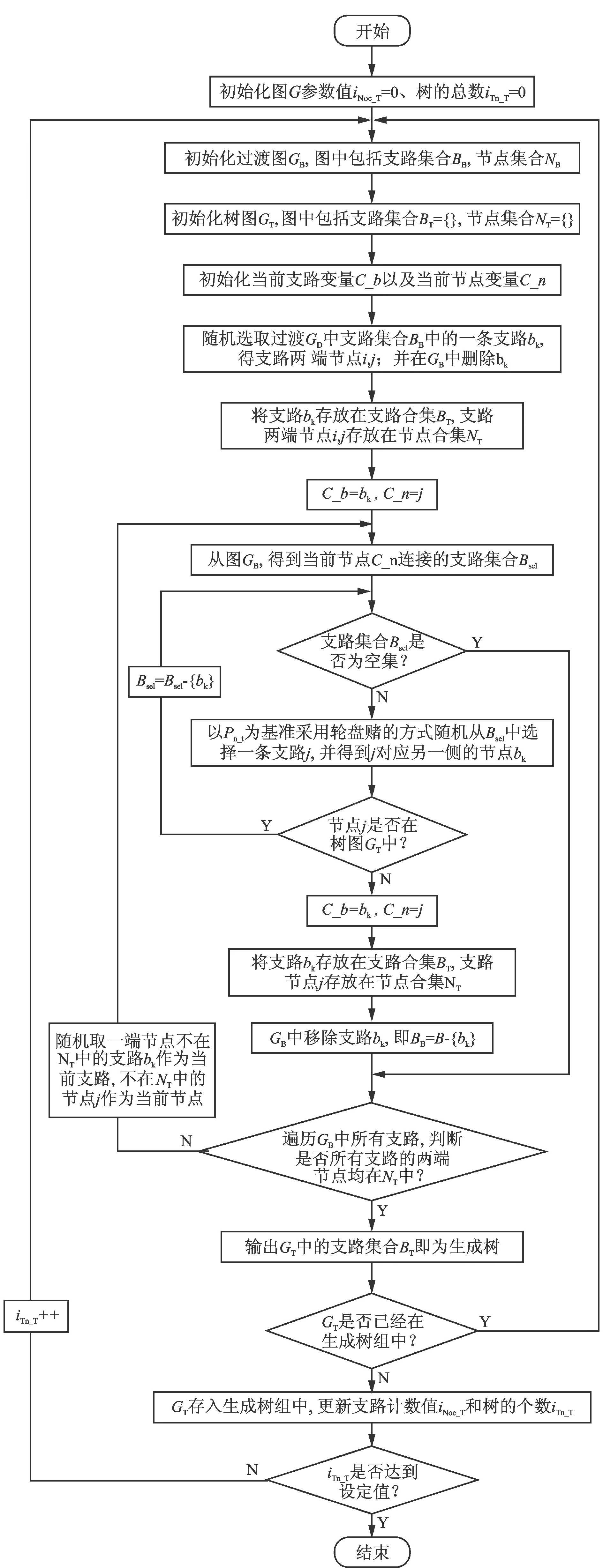
图4 随机生成树算法流程图Fig.4 Flow chart of random spanning tree algorithm

步骤5：判别新生成的生成树GT成与生成树组中已有的生成树是否相同，相同转步骤1，不相同则存入生成树组，同时图G更新支路计数值iNoc_T++；树个数iTn_T++。

步骤6：判断是否达到设定循环次数，即生成树的个数iTn_T是否达到设定的值，若达到则退出运行，否则，转步骤2。

3 算 例

在VS2015平台下用VC++编制了提出的生成树算法，分别用图1中的复杂图和图7中的PG & E69节点电力系统图为例对提出的算法进行了验证。

3.1 算例1

对图1中的复杂图简化后得简化图2，对简化图2中的节点和支路进行分类并处理，使用文中提出的方法共生成291个简化图对应生成树图，表5为图的生成树连支组(仅列出10组)；生成2 227个图1对应生成树，表6为复杂图的生成树连支组(仅列出10组)。

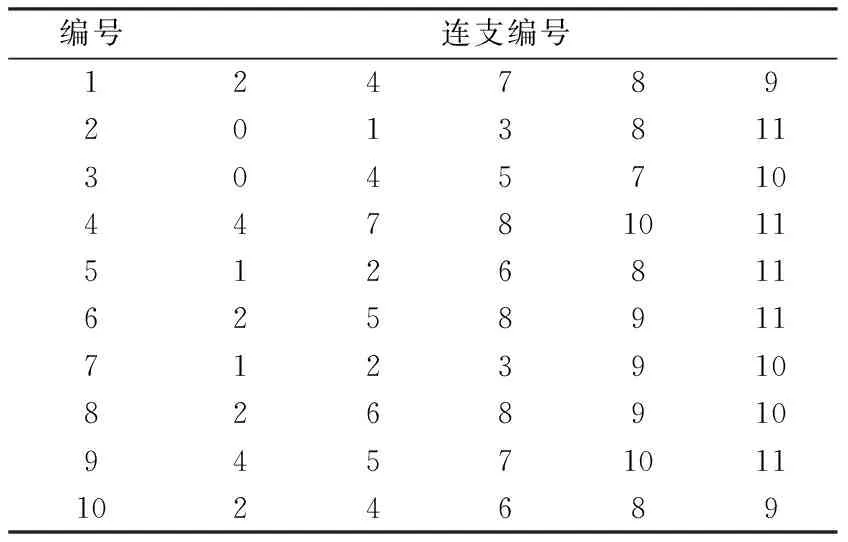
表5 简化图生成树对应连支组Tab.5 Connected branch group corresponding to spanning tree of simplified graph

从表5结果可以看出，本文中方法可以生成简化图对应的生成树图，方法正确有效。图5为简化图2断开支路集{2,4,7,8,9}得到的一个生成树图。

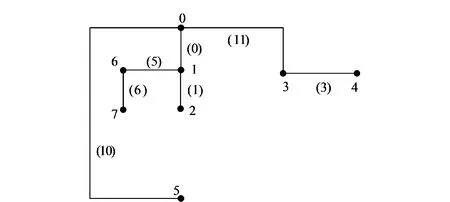
图5 简化图2对应的一种生成树图Fig.5 A spanning tree graph corresponding to simplified graph in Fig.2

针对图5中的生成树图逆用简化规则，将简化图中断开的支路对应的互斥支路集任一支路打开，并将删除得辐射式支路重新添加即可得复杂图对应的生成树图。图6为图1中复杂图断开支路集{4,12,25,23,27}得到的一个生成树图，表6为复杂图1对应生成树的结果。

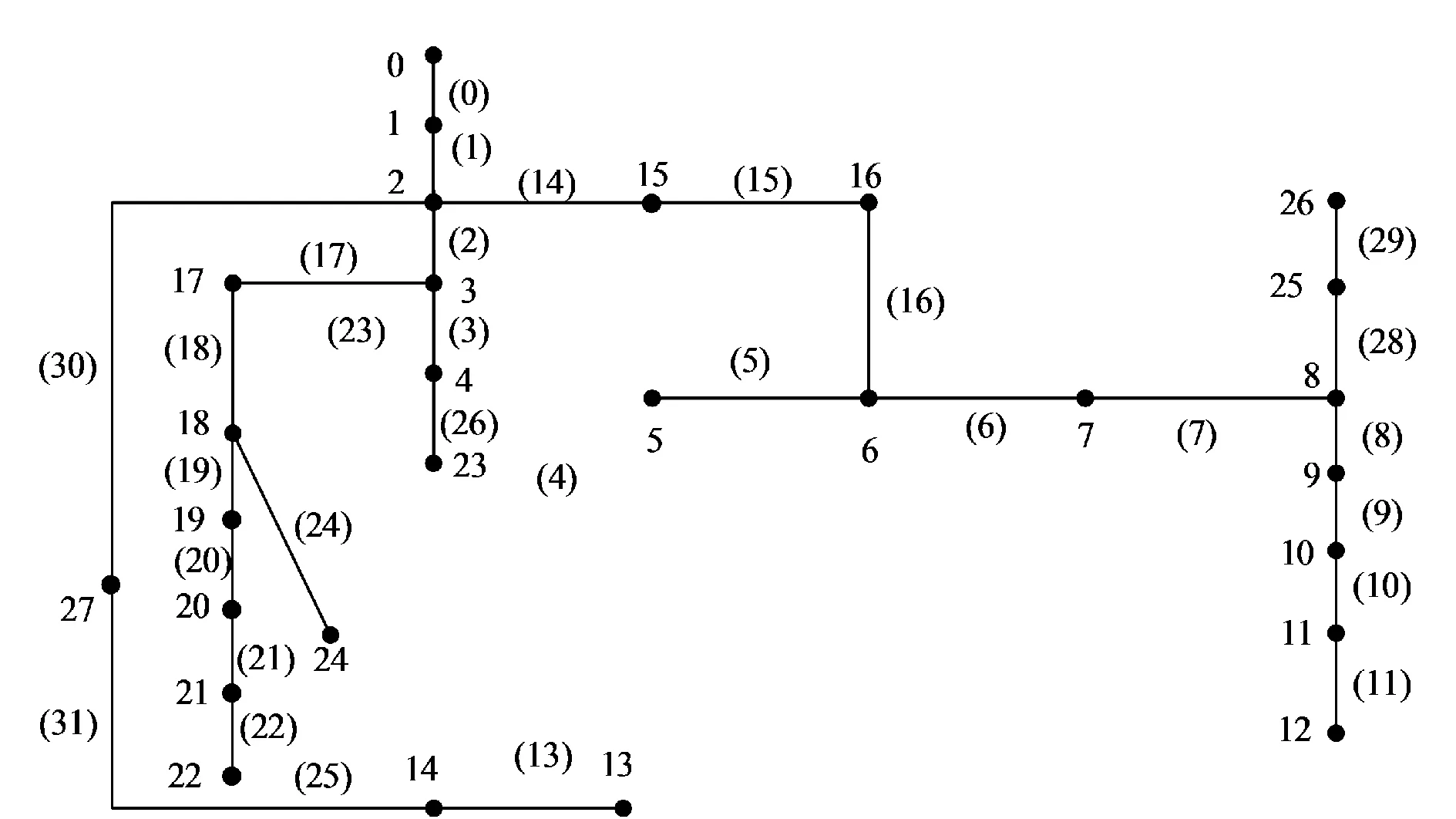
图6 复杂图1对应的一种生成树图Fig.6 A spanning tree graph corresponding to complex graph in Fig.1

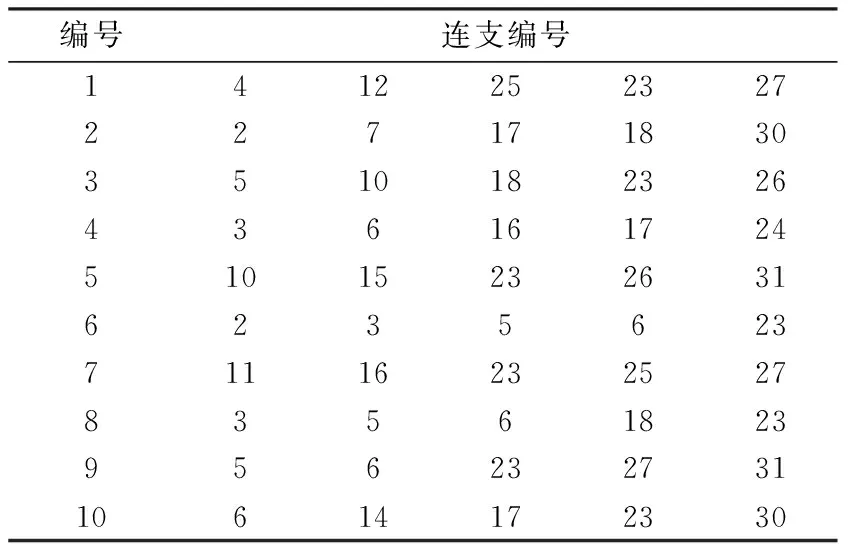
表6 复杂图1的生成树对应连支组Tab.6 Connected branch group corresponding to spanning tree of complex graph in Fig.1

从表6中结果和图6可以看出，本文中方法可以生成复杂图对应的生成树，方法正确有效。

3.2 算例2

图7为PG & E69节点电力系统图，包含支路73条，节点69个。

对图7中的图简化后进行生成树组的计算，共生成6 296组对应的生成树图。图7的生成树连支组见表7(仅列出10组)。如图8所示，列出图7对应的一种生成树图。

表7 69节点系统生成树对应连支组Tab.7 Connected branch groups corresponding to 69 node system spanning tree

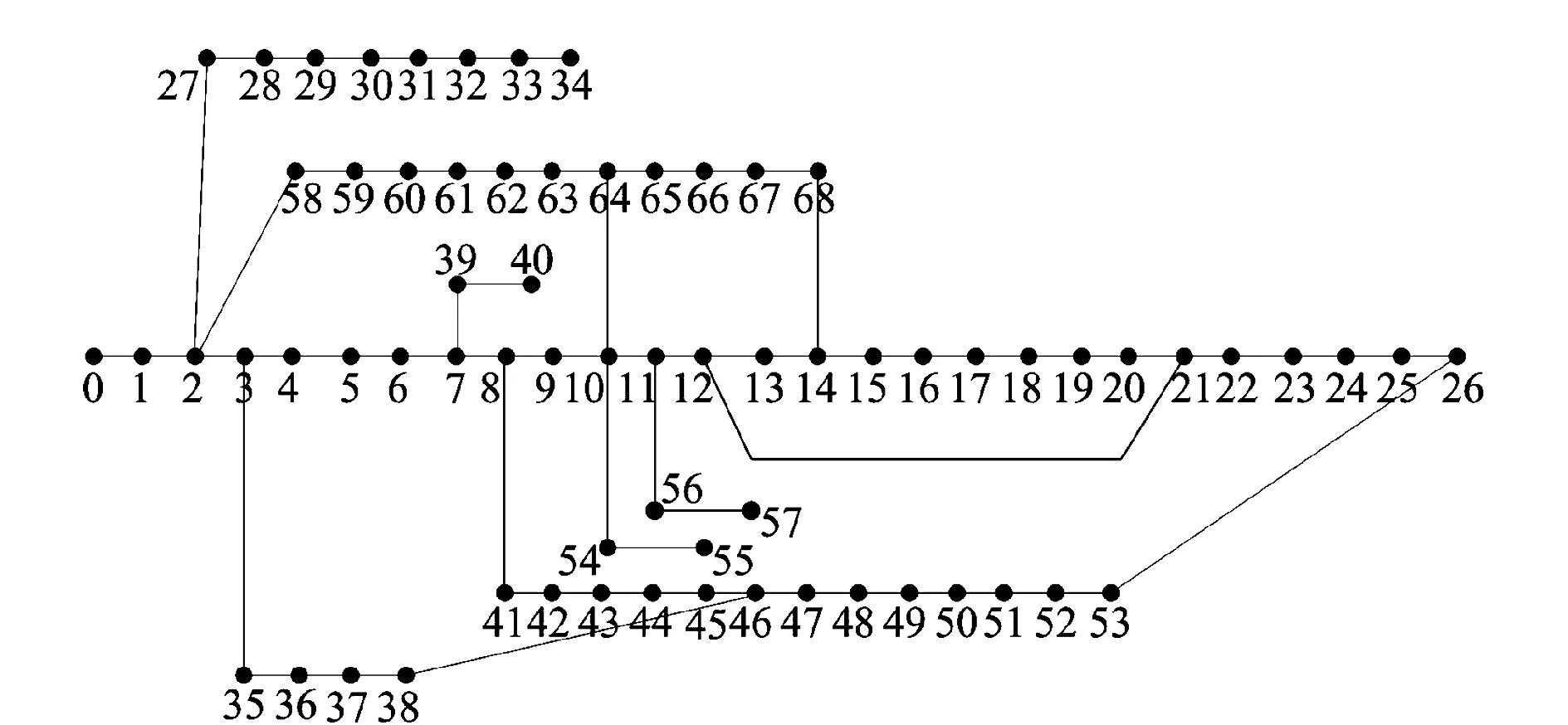
图8 PG & E69节点系统图对应生成树图Fig.8 Spanning tree graph corresponding to PG & E69 node system diagram

从表7中结果和图8可以看出，本文中方法可以正确有效地生成重构可行解图。

3.3 方法性能对比

在相同的连通性判断方法下，分别采用本文中方法和文献[2]的BST算法对图1和图7生成500棵生成树。平均生成一棵生成树计算时间见表8。

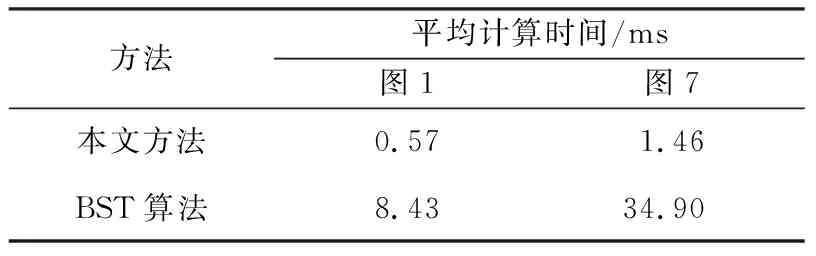
表8 同一算例下不同方法平均计算时间对比Tab.8 Average calculation time of the same example using different methods

从表8可知：针对包含28个节点和32条支路的图1，本文方法的平均计算时间为0.57 ms，文献[2]中的BST算法平均计算时间为8.43 ms,本文方法计算效率为BST算法的14.79倍。针对包含支路73条，节点69个的PG & E69节点电力系统图，本文方法的平均计算时间为1.46 ms，文献[2]中的BST算法平均计算时间为34.90 ms,本文方法计算效率为BST算法的23.90倍。且随着图的规模增加，优势愈发明显。

4 结 论

本文对复杂连通图中得到生成树的算法进行了研究。将复杂图按照简化规则简化后得到简化图。在简化图的基础上，利用提出的生成树算法得到对应的生成树图，进而生成复杂图对应的生成树图。算例表明，方法具有以下特点：

(1)该方法可正确生成复杂连通图对应的简化图。

(2)该方法针对简化单图后可正确地、快速地求其所有的对应生成树图。

(3)针对简化图对应生成树图，可逆向使用简化规则得到复杂图对应的所有生成树图。

(4)该方法相比其他方法，能大幅度提高复杂图对应生成树搜寻过程中的速度，且随着连通图规模的增大，该优势越发明显。