一类Minkowski空间里的格序半群

宋元凤，李武明，杨 柳

(1.通化师范学院数学学院，吉林 通化 134000；2.吉林大学数学学院，吉林 长春 130012)

0 引言

序半群作为序代数的一个分支，近30年来得到了蓬勃发展，而格序半群作为格代数和半群代数的比较完美的结合成为了序半群的重要部分.1948年美国著名数学家Birkhoff[1]论述了格序半群的相关知识.之后，在Fuchs[2-3]和Holland[4]等数学家的推动下，格序半群已发展成一个相对完整的研究系统.Birkhoff、Conrad、Kontorovi等数学工作者丰富了这个领域的结论[5-11].

1907年德国数学家Minkowski将Einstein与Hendrik Antoon Lorentz理论结果重新表述成(3+1)维的时空，称为Minkowski空间.[12]Minkowski空间理论经历了一百多年发展，对(3+1)维Minkowski空间理论的研究已经推广到p+q维Minkowski空间理论——(p，q)型Minkowski空间理论的研究中[13].(p，q)型Minkowski空间即为实Clifford代数Clp，q的生成空间——实数域上的正惯性指数为p、负惯性指数为q的线性空间Rp，q.当p=n-1，q=1时，(p，q)型Minkowski空间Rp，q称为n维Minkowski空间，简记为Mn.

对实Clifford代数的结构已经有了比较深入的研究[14-16].本文研究实Clifford代数生成空间，给出了实Clifford代数生成空间——(p，q)型Minkowski空间Rp，q的M-距离概念，然后通过M-距离这个工具把实Clifford代数的一类生成空间——n维Minkowski空间Mn分成4个区域，并探讨了这些区域的格序半群与格序半线性空间结构.

1 (p，q)型Minkowski空间的M-距离与E-距离

实Clifford代数Clp，q可以展开写成[17]

Clp，q=〈Clp，q〉0⨁〈Clp，q〉1⨁…⨁〈Clp，q〉p+q.

实Clifford代数Clp，q的子空间

Rp，q=〈Clp，q〉1={x1e1+…+xpep+xp+1ep+1+…+xp+qep+q|x1，…，xp+q∈}

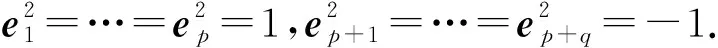
定义1[13]Rp，q是实数域上的线性空间，在Rp，q上定义一个二元实函数，对Rp，q中任意ω=x1e1+…+xp+qep+q，χ=y1e1+…+yp+qep+q，定义ω，χ的M-内积为

ω·χ=(x1e1+…+xp+qep+q)·(y1e1+…+yp+qep+q)=
x1y1+…+xpyp-xp+1yp+1-…-xp+qyp+q，

记作ω·χ，称赋有Minkowski内积的线性空间Rp，q是(p，q)型Minkowski空间，其中γ=x1e1+…+xpep是向量ω的空间分量，τ=xp+1ep+1+…+xp+qep+q是向量ω的时间分量.Rp，q中的向量可以分为3类，当ω·ω=0，(>0，<0)时称ω是Rp，q的类光(类空，类时)向量.规定零向量既是类空向量，也是类时向量和类光向量.

通过Minkowski空间向量的M-内积定义Minkowski空间的M-距离(模)(或称时空间隔)，记作‖‖M.同时为了区分Minkowski空间的M-距离(模)，把Euclid空间的距离(模)叫作E-距离(模)，记作‖‖E.

定义2 Minkowski空间Rp，q中向量

ω=γ+τ=(x1e1+…+xpep)+(xp+1ep+1+…+xp+qep+q)

的M-距离(模)为

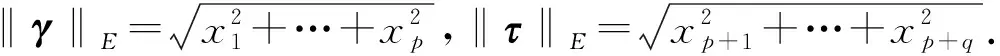
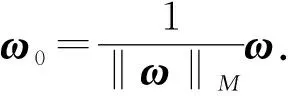
Minkowski空间Rp，q的所有类时向量的集合为

Ω={ω∈Rp，q|ω=γ+τ，γ=x1e1+…+xpep，τ=xp+1ep+1+…+xp+qep+q，‖γ‖E<‖τ‖E}.

把{ω=γ+τ|ω∈Rp，q，‖γ‖E<‖τ‖E，xp+1>0，…，xp+q>0}称为Rp，q的未来类时区，记为Rp，q+，把{ω=γ+τ|ω∈Rp，q，‖γ‖E<‖τ‖E，xp+1<0，…，xp+q<0}称为Rp，q的过去类时区，记为Rp，q-.

例1 设Rp，q，pq≠0为(p，q)型Minkowski空间，令S=Rp，q+∪Rp，q-，那么S对加法不封闭.

2 n维Minkowski空间Mn子集的格序半群结构

定义3[18]若偏序集G中任意两个元素都有上确界和下确界，把G中元素a和b的上确界和下确界分别记为a∨b和a∧b，即a∨b=sup{a，b}，a∧b=inf{a，b}，则称偏序集G为格.

定义4[18]设G是半群且(G，∨，∧)是格.若

(a∨b)c=ac∨bc，c(a∨b)=ca∨cb，∀a，b，c∈G，

则称(G，·，∨，∧)是半格序半群(∨半群).一个∨半群若满足

(a∧b)c=ac∧bc，c(a∧b)=ca∧cb，∀a，b，c∈G，

则称G是格序半群.

定义5[18]设G是半环A上的半线性空间.如果存在半序关系使得(G，)是半序集，则称G是半环A上的半序半线性空间.如果半序集(G，)为格，则称G是半环A上的可格半线性空间.

本文称Mn={x1e1+…+xn-1en-1+xnen|x1，…，xn∈，为n维Minkowski空间.Mn的向量内积为

ω·μ=(x1e1+…+xn-1en-1+xnen)·(y1e1+…+yn-1en-1+ynen)=
x1y1+x2y2+…+xn-1yn-1-xnyn，∀ω，μ∈Mn.

易知，Rn-1={ω∈Mn|xn=0}为n-1维欧氏向量空间，它是n维Minkowski空间Mn的子空间.对于任意γ1，γ2∈Rn-1，‖γ1+γ2‖M≤‖γ1‖M+‖γ2‖M，即2个向量的M-模满足三角不等式.

记

C(ω0，0)={ω|‖ω-ω0‖M=0，ω，ω0∈Mn}，

它是以ω0=x11e1+…+x1(n-1)en-1+x1nen∈Mn为中心的点球.在n维欧氏空间里点球是一个点，但是在n维Minkowski空间里点球不是一个点.以ω0=x11e1+…+x1(n-1)en-1+x1nen∈Mn为中心的点球方程是(x1-x11)2+…+(xn-1-x1(n-1))2=(xn-x1n)2，于是可知在n维Minkowski空间里两个点球一定相交.

例如，三维Minkowski空间里，设C(ω1，0)，C(ω2，0)为两个不同点球，则它们的交集方程是

其中：ω1=x1e1+y1e2+z1e3，ω2=x2e1+y2e2+z2e3.将之变形为

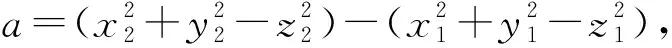
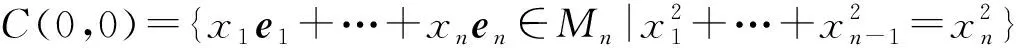
(1)Mn(1)={ω|ω=γ+xnen，‖γ‖E≤xn}；

(2)Mn(2)={ω|ω=γ+xnen，‖γ‖E≥xn，xn>0}；

(3)Mn(3)={ω|ω=γ+xnen，‖γ‖E≤-xn}；

(4)Mn(4)={ω|ω=γ+xnen，‖γ‖E≥-xn，xn<0}.

上面式子中γ=x1e1+…+xn-1en-1.在n维Minkowski空间Mn里4个区域Mn(i)中定义序关系i，i=1，2，3，4，ω1iω2⟺ω2-ω1∈Mn(i)，i=1，2，3，4.

引理1n维Minkowski空间Mn的子集Mn(1)，Mn(3)对于“+”是半群.

证明只证明n维Minkowski空间的子集Mn(1)对于“+”是半群，类似可以证明Mn(3)对于“+”是半群.

设ω1=γ1+x1nen，ω2=γ2+x2nen是Mn(1)的任意两个向量，其中‖γ1‖E≤x1n，‖γ2‖E≤x2n.因为ω1+ω2=γ1+γ2+(x1n+x2n)en，‖γ1+γ2‖E≤‖γ1‖E+‖γ2‖E≤x1n+x2n，所以n维Minkowski空间Mn的子集Mn(1)对于“+”是封闭的.容易验证Mn(1)对于“+”满足结合律，因此Mn(1)为半群.

因为在Mn(1)，Mn(3)中每一非零元没有逆元，所以Mn(1)，Mn(3)不是群.

定理1n维Minkowski空间Mn的子集(Mn(1)，+)关于序1，(Mn(3)，+)关于序3都为格序半群.

证明只证明半群(Mn(1)，+)关于1为格序半群，类似地能够证明半群(Mn(3)，+)关于3也为格序半群.

在Mn(1)中，设ω1=γ1+x1nen，ω2=γ2+x2nen为任意两个向量，其中‖γ1‖E≤x1n，‖γ2‖E≤x2n.当ω1，ω2有偏序关系时，不妨假设ω11ω2，构造ω1∧ω2=ω1，ω1∨ω2=ω2.当ω1，ω2没有偏序关系时，构造于是Mn(1)是格.经验证知：

ω1+(ω2∧ω3)=(ω1+ω2)∧(ω1+ω3)，

ω1+(ω2∨ω3)=(ω1+ω2)∨(ω1+ω3).

通过引理1可知Mn(1)为半群，因此半群Mn(1)为格序半群.

推论1 半群(Mn(1)，+)关于序1，(Mn(3)，+)关于序3都构成实数域上格序半线性空间.

设ω0=γ0+x0nen是n维Minkowski空间Mn中的已知向量，令：

(1)Mn(1，ω0)={ω|ω-ω0=γ+xnen，‖γ‖E≤xn}；

(2)Mn(2，ω0)={ω|ω-ω0=γ+xnen，‖γ‖E≥xn，xn>0}；

(3)Mn(3，ω0)={ω|ω-ω0=γ+xnen，‖γ‖E≤-xn}；

(4)Mn(4，ω0)={ω|ω-ω0=γ+xnen，‖γ‖E≥-xn，xn<0}.

上面式子中γ=x1e1+…+xn-1en-1.

推论2n维Minkowski空间的子集(Mn(1，ω0)，+)关于序1，(Mn(3，ω0)，+)关于序3为实数域上格序半线性空间.