一种基于稀疏搜索的激活噪声快速聚类算法
郭林亮,韩旭明,张逸航
(1.长春工业大学数学与统计学院,吉林 长春 130012;2.暨南大学信息科学与技术学院,广东 广州 510632;3.长春工业大学计算机科学与工程学院,吉林 长春 130012)
0 引言
聚类分析是无监督学习中的重要方法.在样本没有给定类别信息的情况下,聚类分析根据计算样本特征的相似性来确定样本的分组,同一分组的样本具有高度的相似性,而来自不同分组的样本之间相异度高[1].聚类算法可以以无监督的方式找到数据的特征分布结构,所以研究者们提出了很多不同类型的聚类算法,并被广泛应用于以空间信息处理为代表的众多领域[2],例如,图像分割、模式识别等[3-6].
大多数现有的聚类算法在处理局部和非线性数据模式方面都有很大的局限性[7].针对形状复杂、噪声比较多的数据集,这些聚类算法没有很好地解决参数多且不易调节的问题,且对噪声和紧邻类之间的连接点的分配也不合理.
实现聚类的众多方法中,基于密度的聚类方法是比较流行且高效的.文献[8]利用密度可达的方式去链接eps邻域获得子簇;在此基础上,研究者们提出了许多变体算法来获得更好的聚类性能[9];文献[10]提出了一种快速的近似KNN的算法来判断和确定核心块、非核心块和噪声块;文献[11](DPC)选取乘积较大的几个点作为聚类中心,从而确定类的个数;文献[12](FSDPC)设计了一种新的稀疏搜索策略来衡量每个数据点的最近邻居之间的相似性;文献[13]设计了一种数据点关联度转移方法和分层方法来选择聚类中心;文献[14](DPC-DBFN)使用基于k近邻的模糊核密度对决策图进行分区来确定类的个数,同时分配边界区域和噪声;文献[15]提出在一定半径邻域寻找最大密度点,并把它们作为聚类中心,避免了选择聚类中心个数的问题;文献[16]采用覆盖树的方法快速计算数据点密度;文献[17]采用了树的结构获得初始的子类,再计算这些子类的相似度来进行层次聚类;文献[18]先采用近邻的方式获得基本的簇,再通过图的方式进一步分割这些簇;文献[19]以共享近邻的方式确定数据点的密度,并选择密度最大的几个数据点作为代表点进行层次聚类得出最后的聚类结果.
以上的聚类算法取得了一定的成就,但还存在以下不足:算法虽然减少了运行时间成本,但却降低了边界点和噪声分配的效率;在处理彼此靠近类的连接处的点时,由于预设的参数较多,引起连锁反应导致噪声点没有有效分配,使聚类结果出现偏差.
为了解决这些问题,本文提出了一种基于稀疏搜索的激活噪声快速聚类算法(ANSC).本文算法利用数据总体离散度与个体近邻属性的关系重构密度函数,把分布结构复杂的数据点映射到简单的自定义密度函数上,通过观察密度函数的性质来激活潜在的噪声.按照有规律的步长规则快速寻找稀疏互连点,并以粗化和细化分割数据点的方式共建这些互连点形成子类,利用子类间距离的分布特性来合并.在获得初步的聚类结果后,根据噪声的分布特点判断是否形成新的目标类.因此,对于不同形状的数据集,针对如何处理噪声、减少参数的数量和降低时间成本的问题,本文提出了ANSC.
1 ANSC
1.1 激活噪声
提出的算法使用近邻的方式确定数据点的密度,这种方式可以反映数据的总体离散度和个体近邻之间的关系.当一个数据点与周围点的距离和标准差较大时,它的密度会很小,甚至小于0.这种方式可以把分布结构复杂的数据点映射到密度函数上,通过观察函数的性质挖掘潜在的噪声.与神经网络中设置的激活函数的意义类似,认为在密度小于0的数据点是不需要被关注的点,并把这些点定义为噪声,实现激活的作用.
为了减少重复的距离计算,算法采用快速k近邻的方法(如kd-tree[20]),仅通过搜索近邻以减少数据点间距离的计算次数.此过程只设计一个易于调节的近邻参数k.这种设置方式减少了聚类过程中参数的数量.
假设数据集为X={x1,x2,…,xn},其中n是数据点的个数.数据点xi与所有近邻距离的和Dis(xi)=sum(knn_dist(xi,:)),其中knn_dist(xi,:)代表数据点xi的近邻距离的集合.定义Dis={Dis(x1),Dis(x2),…,Dis(xn)}.
借助数据近邻和标准差与离散度的关系,定义了总体离散度Gdis的概念,定义为
(1)
其中:d是数据的维度,mean表示求数据的均值,max表示求数据的最大值,st是所有st(xi)的集合,st(xi)代表数据点xi与所有近邻点的标准差.
为了体现数据个体与总体的离散关系,有效地确定噪声,定义了数据点的密度函数为
(2)
从公式(2)可知,随着总体离散度的增加,数据个体的密度在逐渐减小,当密度小于0的时候,则认定数据点为噪声.如果一个数据集中密度小于0的点比较多,则数据集中的噪声也很多,能够反应这个数据集的数据分布比较松散,为后续的识别和判断噪声的类别提供了基本的保障.在实验中可以改变近邻的个数来实现数据点密度的变化,从而确定不同的噪声点和类连接处的点.
1.2 近邻互连共建子类
与现有的构建子类的方法不同,本文以步长的方式稀疏搜索数据确定互连点,再以先粗化后细化的分割方法共建这些点形成子类.按照类与类的性质,相似性大且距离比较近的点属于一个类的几率更大.
基于以上想法,本文提出在一个随机数据点的最大近邻索引的基础上,设置一个步长去寻找下一个数据点的方法.同时,定义以这种方式寻找到的数据点为互连点.如果互连点间满足一定的阈值条件,就链接这些互连点形成子类,这个过程叫作粗化共建.在此基础上,为了进一步分裂彼此靠近的类,需要细化共建这些互连点.选择每个子类中密度最大的点为代表点,代表子类,并把这些代表点称为共建点.
假定搜索到的互连点个数为n1,所有的数据点都是未访问点.
粗化共建:找到第一个未访问的互连点xi及它的近邻,在此基础上,不断寻找其他互连点.若两个数据点索引之间满足以下条件,则停止粗化共建,并标记这些互连点为已访问:
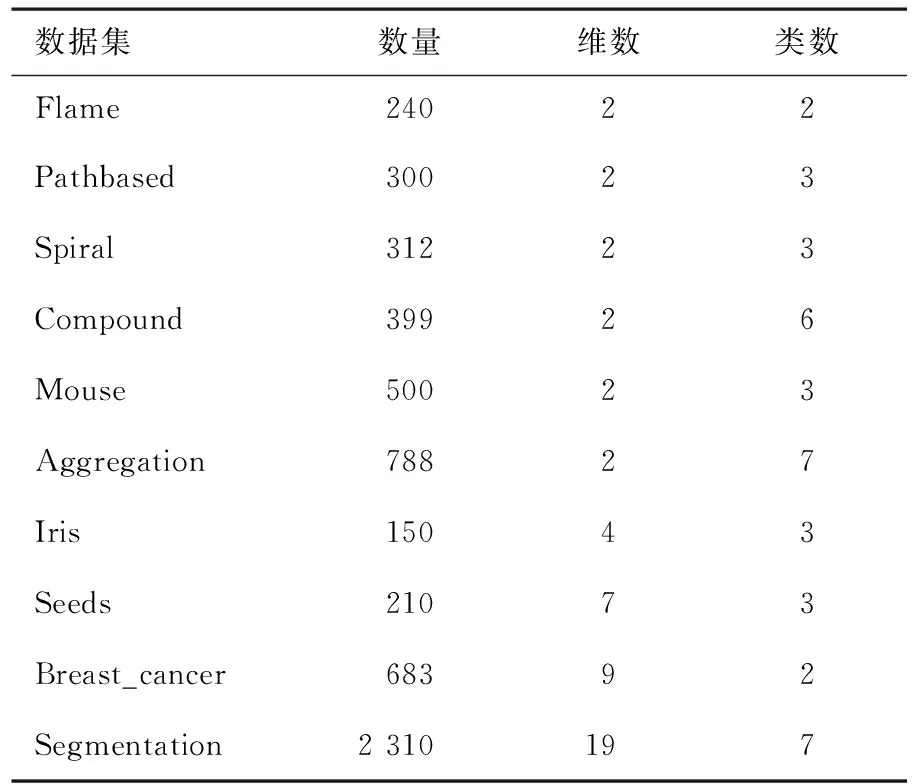
Index(xi)-Index(xc) (3) 此时xc是当前需要判断类别的数据点,Index(xi)代表数据点xi的索引. 细化共建:在粗化共建的基础上,寻找未访问的第一个互连点.若数据点索引之间满足以下条件,则进行细化共建,并标记这些互连点为已访问: (4) 其中:knnj(xi)表示离xi最近的第j个点,Round表示向上取整函数. 由共建点的定义可知,共建点是子类中密度最大的点.如果两个共建点之间的距离小于共建点间的最小距离均值时,就认为它们代表的子类应该属于一个类,所以需要合并一些相似度大的子类.这种合并的方式与层次聚类相似,但是实现途径是不同的.本文算法中类的个数可以根据共建点的分布特点自动地确定,无须的人为的干预.对于所有的剩余点,未访问的点归类于最近的类. 为了减少噪声对聚类结果的影响,提出两种分配噪声的方法:一是连续出现噪声的个数n3;二是噪声与它的近邻之间的关系.如果连续出现很多噪声,则认为这些噪声可以构成一个新的类,并把它们定义为近类噪声.如果当前噪声与近邻所属的类距离比较远,把这些点形成一个新的类,并定义它们为远类噪声. 假定当前的聚类结果中有n2个子类,每个子类中数据点的个数分别是{num1,num2,…,numn2}. 近类噪声:存在连续的噪声,且它们的个数和为n3,如果满足以下条件: n3>(num1+num2+…+numn2)/n2. (5) 远类噪声:假定噪声为点noi,它与最近邻点knn1(noi)的距离为Ndis,它的第k个近邻为knnk(noi),Kdis是knnk(noi)所有近邻距离的平均值,满足以下条件: Ndis>n2*Kdis. (6) 本文提出的算法由以上3个模块组成,描述如下: 第1步:按照公式(2)获取每个数据点的密度,根据密度的大小来确定噪声点; 第2步:随机选择一个初始点,如果初始点的最大近邻不是噪声点,则把最大近邻点认为是第一个互连点,在此互连点的基础上以4*k的步长寻找下一个初始点;否则以2*k的步长寻找下一个初始点,直到所有的数据点都被搜索结束; 第3步:通过第2步可以获得很多个互连点,把所有的互连点组成一个新的数据集,在此基础上获得共建点,再按照公式(3)和(4)定义的方式获得粗化共建和细化共建的子类; 第4步:就近分配未访问点,按照公式(5)和(6)的原则去分配近类噪声或者远类噪声; 第5步:得到最后的聚类结果. 本文计算数据点密度的时间复杂度是O(nlogn).在近邻互连共建子簇、合并子簇和分配剩余数据点的过程中,只计算互连点之间的距离,而互连点的个数远小于数据个数,所以这部分的时间复杂度不高于O(n).综上所述,ANSC的算法的时间复杂度为O(nlogn),小于对比算法的时间复杂度O(n2). 为了验证ANSC算法的有效性,使用最新聚类研究中经常使用的10个人工和真实数据集进行实验.ANSC与最新的聚类算法进行了比较,包括算法FSDPC[12]、DPC-DBFN[14].为了排除对比算法在改变参数时对聚类结果的影响,在实验过程中采取多次微调参数的方式,并选用最好的评价指标作为聚类结果.所有算法的实验都是在MATLAB 2018 a环境上实现的.所有数据集的信息如表1所示,它们都来自UCI 数据库. 表1 全部数据集 为了进一步比较3种聚类算法在10种数据集上的聚类方法可靠性和性能,本文使用3种常见的外部聚类评价指标,包括准确度(ACC)、归一化互信息(NMI)[21]、调整兰德系数(ARI)[22].若这些指标的值越大越好,越接近1,则表示聚类算法的实际效果越好.在人工和真实数据集上的实验结果如表2所示. 表2 3种算法在3个评价指标上的结果 在实验中,算法采用的聚类准确度评价指标ACC定义为 根据表2的实验结果可知,在解决不同形状的人工和真实数据集时,所提出的算法都是可行的,提高了聚类算法的性能指标,并且3个性能评价指标都是最高的.对于对比算法,算法DPC-DBFN的聚类效果在解决非凸数据集时,效果是最差的;算法 FSDPC比DPC-DBFN展示了更好的聚类结果,但是在解决密度不均匀的数据集时,两个算法的聚类结果表现都一般. 通过以上实验结果的分析,所提出的ANSC对非凸数据的边界和类连接处点的处理方式是有效的;从3个聚类的评价指标可知,相对于2个较新的对比算法,本文算法对非凸数据集是有效且高效率的聚类. 本文针对聚类算法中对噪声和边界分配不合理的问题,提出了一种基于近邻互连共建的ANSC.此算法包括3个核心部分:激活潜在的噪声;以步长的方式快速搜索互连点来达到共建子簇;判断噪声类型.本文算法利用数据总体离散度与个体近邻属性的离散关系重构具有代表性的密度函数来获得噪声;通过快速确定近邻互连点来获得新的共建数据点;通过噪声的分布特点来优化其类别. 与较新的聚类算法相比,在10个人工和真实数据集上的实验结果表明,本文提出的方法在噪声和类连接处点的合理分配问题上是有效的和可靠的.在预设参数少和运算时间成本低的情况下,提高了聚类算法的效率和性能.1.3 识别和检测噪声
1.4 时间复杂度分析
2 实验结果
2.1 实验对比
2.2 性能评估

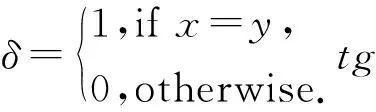
2.3 结果与分析
3 结论

