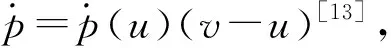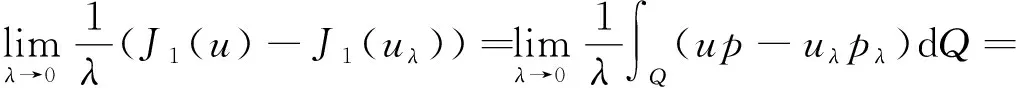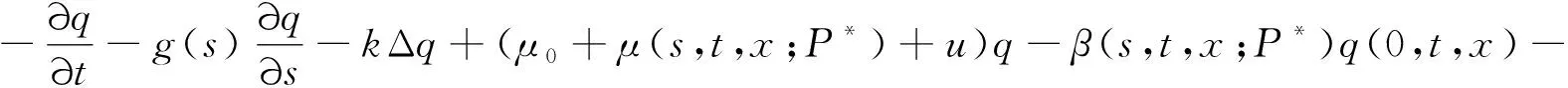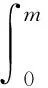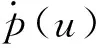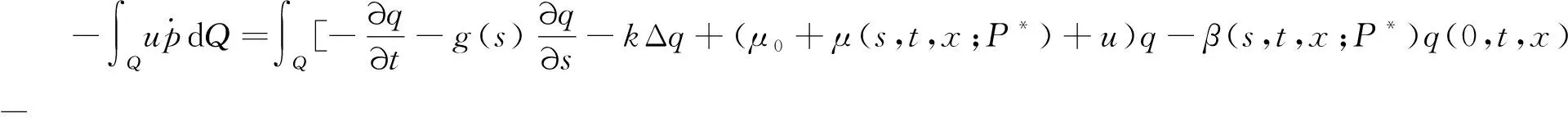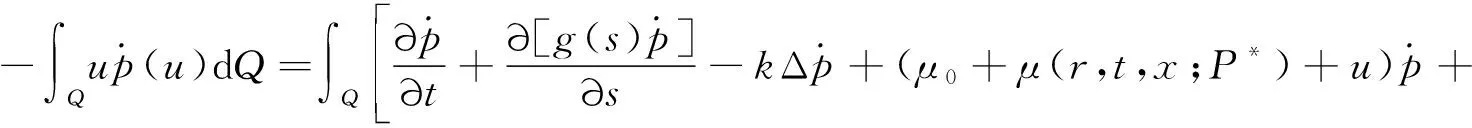周期环境下尺度结构随机种群扩散系统的最优收获
卜 红 彧
(辽东学院师范学院数学系,辽宁 丹东 118003)
1 问题的提出
在种群问题的研究过程中,考虑到种群拥挤和生存环境限制对种群发展过程的影响,相应的数学模型关于状态函数就是非线性的.文献[1]研究了年龄和时滞的非扩散种群系统的最优生育率控制;文献[2]研究了年龄结构和加权的随机种群系统的最优边界控制;文献[3]研究了一类污染环境下具有扩散和年龄结构的随机种群系统强解的存在唯一性;文献[4]研究了一类非随机周期种群系统的最优收获;文献[5]研究了尺度结构的非扩散随机种群系统的最优输入率控制;文献[6-8]研究了个体尺度结构下竞争种群系统的最优收获控制、最优边界控制和最优输入率控制;文献[9]研究了非随机种群扩散系统的最优收获条件.在上述基础上,基于周期环境,只有考虑到种群的尺度结构、扩散系数和随机因素的影响,才更加符合种群生存的实际.本文讨论如下具有尺度结构的随机种群扩散系统(P):
(1)
在上述模型中:固定常数m,T分别表示种群个体最大尺度和系统演变周期,0
(2)
讨论下面的最优收获控制问题:寻找u∈U,使得
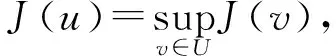
(3)
其中容许控制集为
U={v∈L∞(Q)|0≤v(s,t,x)=v(s,t+T,x)≤L<+∞,a.e.于Q内}.
2 基本假设
本文假设如下条件成立,其中Mi(i=1,2,…,6)为常数:
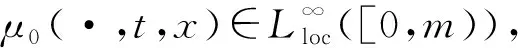
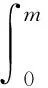
(H2)μ(s,t,x;y)与β(s,t,x;y)关于y二次连续可微,且
0≤μ(s,t,x;y),β(s,t,x;y),|μy(s,t,x;y)|,|βy(s,t,x;y)|≤M2a.e.于Q×+上,
μ(s,t+T,x;P(t+T,x))=μ(s,t,x;P(t,x)),β(s,t+T,x;P(t+T,x))=β(s,t,x;P(t,x));
(H3) 0≤p0(s,x)≤M3<+∞ a.e.于Ωm内,满足相容性条件:
(H4)g(s)是(0,m)上连续可微增函数,0 (H5) 连续函数g′(s,t,x)满足g′(s,t,x)=g′(s,t+T,x); (H6) 0≤k(s,t,x)≤M6<+∞于Q内. 按照文献[10]引进一些记号:设H1(Ω)是Ω上的一阶Sobolev空间,即 V=L2(0,T;H1(Ω))是定义在[0,T]上取值在H1(Ω)中的Hilbert空间.V′为V的对偶空间L2(0,T;(H1(Ω))′). 定理2[4]设(H1)—(H6)成立,则问题(3)在U中至少存在一个最优控制u∈U. (4) 其中: uλ=u+λ(v-u),0<λ<1;pλ=p(uλ);p=p(u). (5) 由(4)和(5)式有 (6) (7) (6)与(7)式作差,将所得方程两端除以λ>0,令λ→0+易得 (8) 定理3 设u∈U是问题(3)的最优收获控制,则u∈U满足 (9) 证明由性能指标泛函J(v)的结构式(2)和u∈U为最优收获控制及(5)式,对0<λ<1得 为了变换(9)式,定义如下的共轭系统: (10) q(s,t,x)=q(s,t+T,x),在Q内; (11) q(m,t,x)=0,在ΩT内; (12) q(s,T,x)=0,在Ωm内; (13) q(s,t,x)=0,在∑上; (14) (15) 上式等号右边关于变量s和t分部积分,并注意到(8)和 (11)—(15)式,得 所以有与(9)式等价的变分不等式: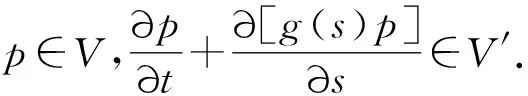
3 最优收获条件