一种与长期项无关的用于求解系统近似解析解的自由迭代法(SFIA)

张 琬，施三支，吴东旭

(长春理工大学数学与统计学院，吉林 长春 130022)

0 引言

众所周知，实际问题的动力学模型通常可以用微分方程组来描述.然而，由于这些方程往往过于复杂，一般很难得到解析解.即使一个精确的解是可以获得的，但经常由于其计算过于复杂而难以实现，因此，寻找这些方程的近似解析解成为许多研究者的研究课题.

摄动方法是最广泛地应用于得到小参数非线性系统近似解的方法，从而将解展开为这个小参数的幂级数.因为存在长期项，传统的摄动方法在实际复杂的系统中不起作用.因此，为了得到显式解，已经开发出各种奇异摄动方法，例如LP法、KBM法、重整化群法[1]、多时间扩张法、变分迭代法[2-4]和同调摄动法[5-8].在这些方法中，由于代数的复杂性，一个更低的近似解通常由摄动方法决定.然而，所有这些方法的一个共同问题是，在近似解中，长期项是不可避免的，因此，为了消除这些导致计算效率低下的长期项，必须付出一些额外的代价.

本文针对非线性常微分系统的近似解问题，提出了一种没有长期项的自由迭代算法(SFIA).通过构造一个简单的迭代过程，可以很容易地以高精度和较少的计算得到近似解，而不需要付出消除长期项的额外成本.

1 SFIA方法

考虑2n维的非线性微分方程

u″(t)+a(t)u′(t)+b(t)u(t)=f(t，u，u′).

(1)

其中：a(t)和b(t)为连续函数；f(t，u，u′)为区域D内一次偏导数有界的非线性函数.简便起见，通过引入两个新的变量

u′=v，v′=-a(t)u′-b(t)u+f(t，u，u′)，

(2)

令

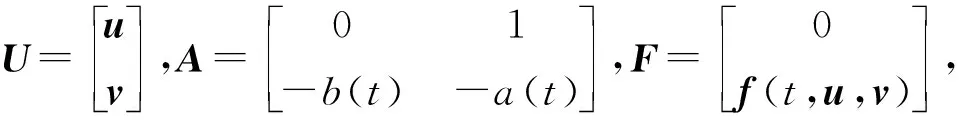
则方程(1)可以简写为

U′=AU+F(t，U).

(3)

假设Φ(t)是线性方程

U′=AU

(4)

的基本解矩阵.对任意t∈D和任意的2n维的常向量u0，方程(3)满足初值条件u0(t)=u0的解等价于下面的积分方程：

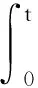
(5)

换而言之，如果u=u(t)是方程(3)的解，那么同样是方程(5)的解.

注意到在式子(5)的右边U中具有未知变量u(t)，因此方程(5)并不能通过简单的计算求得.为了得到方程(5)的解，将上述方程写成如下的等价形式：

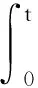
(6)

注意到

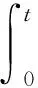
(7)

可以得到

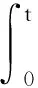
(8)

根据常数变易公式

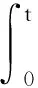
(9)

构造如下简单的迭代公式：

(10)

这一迭代公式非常类似于Picard级数中的迭代公式，可以写成如下的简单形式：

(11)

其中λ称为Lagrange乘子，λ=Φ(t)Φ-1(s).

从形式上看，这个公式与变分迭代法中的公式是十分类似的，但获得Lagrange乘子的途径是完全不同的.在变分迭代法中，需要对上述校正泛函做变分，根据稳定性条件才能得到相应的Lagrange乘子，其中要经过比较复杂的推导过程.本文则由常数变异公式出发确定了迭代公式，并直接给出了Lagrange 乘子的具体形式，并且不需要进行变分处理及稳定性条件等复杂的推导过程，从而在实际计算中增强了实用性且减少了不必要的变分过程带来的复杂运算.问题的关键是根据具体方程能否给出基本解矩阵.

(12)

它的部分和为

(13)

由迭代公式

(14)

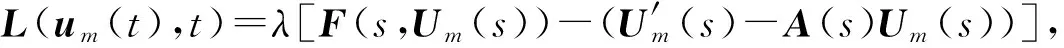
|L(um+1(t)，t)-L(um(t)，t)|≤q|um+1(t)-um(t)|

(15)

成立，且M为L(um(t)，t)在区域D上的一致上界.

由um+1(t)≈um(t)，将(14)式建立为逐步逼近序列

(16)

进行如下估计：

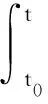
利用数学归纳法，假设对任意正整数n，如下不等式成立：

(17)

那么

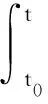
从而对所有的正整数m，有如下估计：

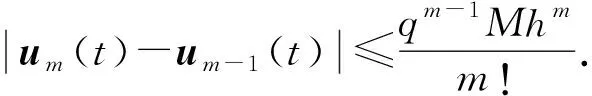
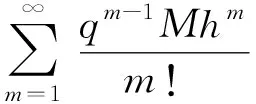
2 关于SFIA方法的应用

例1 考虑下面的非线性系统

(18)

注意到方程(18)的系数均为常数，因此可得基本解矩阵

(19)

通过取初始逼近值y=cost，利用数学工具Maple，可以得到一次稳态近似解

y1(t)=-1.012 5e-0.5tcos(1.322t)-0.487 5sin(2t)-0.512 5cos(2t)+
1.5sint+1.5cost-0.023 6e-0.5tsin(1.32t)+0.25.

图1比较了利用RK方法得到的数值参照解与文中提出的SFIA方法得到的近似解之间关系，显然可见利用SFIA方法得到的近似解与数值参照解之间是非常接近的.

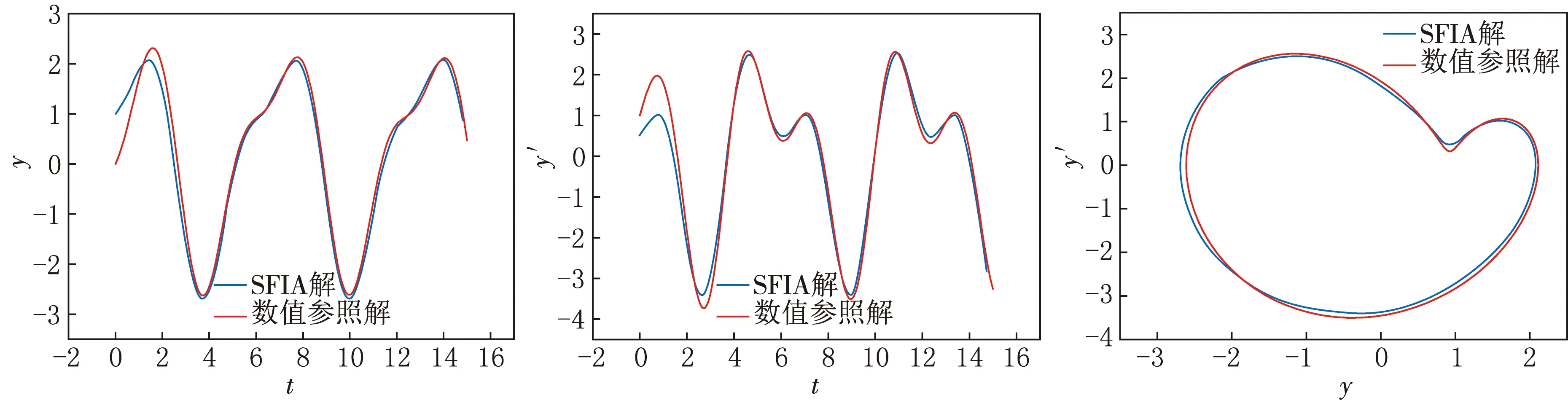
图1 例1 SFIA解与数值参照解比较

从这个例子中很容易看出，SFIA解非常接近参照解，不需要额外的努力就可以消除长期项，这表明了该方法的有效性.

例2 考虑有阻尼的Duffing 系统

(20)

这里ε=0.5.类似于例1，容易得到上述系统的基本解矩阵

(21)

利用初始近似值y=exp(-t)和常用数学软件Maple，可以得到一次稳态近似解析解

(22)

容易看出，这里并没有长期项.

图2显示了相应的y(t)和dy(t)/dt长时间的动力学运动.可以清楚地看出利用SFIA方法得到的一阶近似解非常接近参照解.

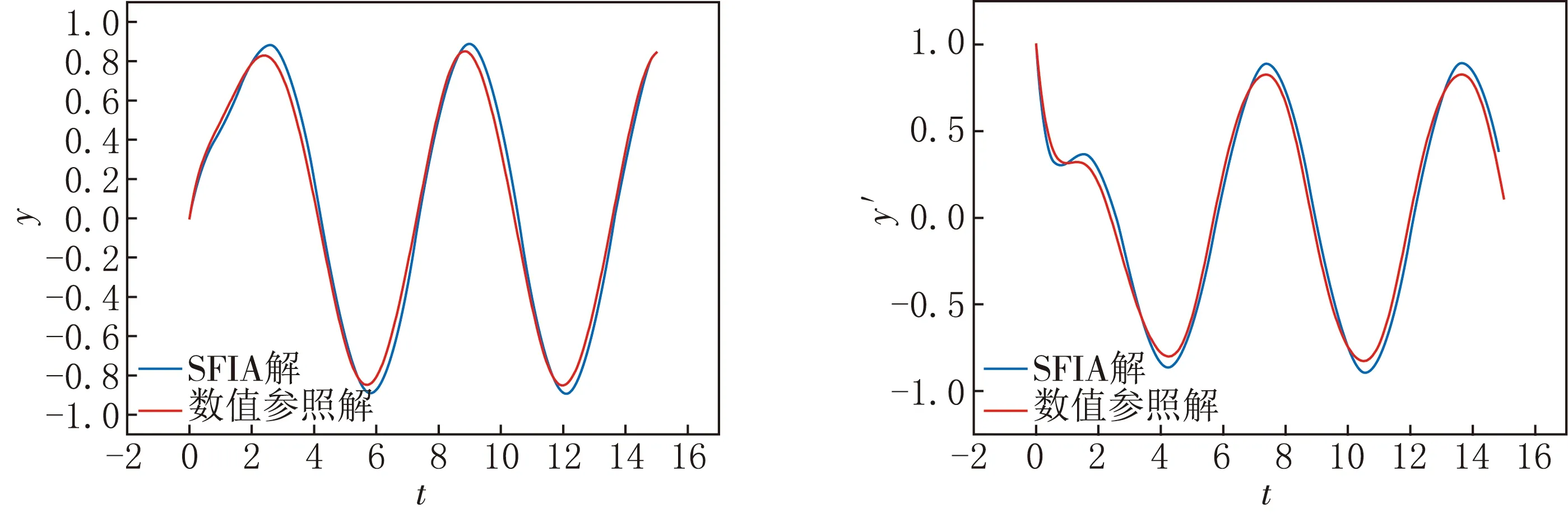
图2 例2 SFIA一阶迭代近似解与数值参照解的比较

再利用自由迭代公式(10)和数学工具Maple，可以很容易得到二阶迭代近似值：

y(t)=-0.136exp(-2t)sin(3t)-0.7cos(t)+0.472sin(t)-0.99e-
exp(-3t)cos(3t)-0.35sin(t)exp(-t)t-0.246exp(-3t)cos(t)-
0.419exp(-3t)sin(t)-0.162sin(t)exp(-2t)t+0.251e-exp(-5t)-
0.535e-2exp(-3t)cos(2t)-0.372e-3sin(t)exp(-6t)+0.36e-
2exp(-4t)+0.489e-2cos(3t)+0.592e-exp(-t)cos(3t)+
1.69exp(-t)sin(t)-0.188e-exp(-4t)cos(2t)+0.9cos(t)exp(-t)-
0.516e-2exp(-3t)sin(2t)+0.837e-2sin(3t)-0.295e-
exp(-t)sin(3t)+0.164e-exp(-5t)sin(2t)+0.10e-
exp(-5t)cos(2t)+0.35cos(t)exp(-2t)-0.243 9cos(t)exp(-4t)-
0.324cos(t)exp(-2t)t-0.609e-sin(t)exp(-4t)-0.487e-
exp(-2t)cos(3t)-0.243sin(t)texp(-3t)+0.19e-exp(-3t)sin(3t)-
0.108cos(t)exp(-t)t-0.585 7e-3cos(t)exp(-7t)+0.769e-5exp(-9t)-
0.508e-3sin(t)exp(-7t)+0.156e-exp(-4t)sin(2t)+0.12e-exp(-3t)+
0.331e-3cos(t)exp(-6t)-0.2sin(t)exp(-2t).

从上面的公式可以看出，第二步迭代中出现类似于te-tsin(t)，te-tcos(t)的项，而并没有类似tsint，tcost的长期项存在.注意到te-tsin(t)，te-tcos(t)等项是随着时间的增加逐渐趋于零的，因此，没有经过任何的额外计算，已经在第二步迭代中消除了长期项，也可以理解为SFIA方法不会产生长期项.

图3展示了利用SFIA方法得到的二阶近似解和参照解之间的比较，可以看出二次近似解十分逼近参照解.

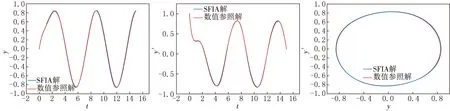
图3 例2 SFIA二阶近似解与数值参照解的比较

图3展示了用SFIA方法得到的二阶近似解与用RK方法得到的参照解之间的比较.它清楚地表明，用SFIA方法所求出的解与参照解非常接近.

例3 考虑Reyleigh方程

(23)

其中ε>0，ε≪1.方程(23)可以改写为

(24)

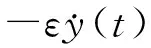
(25)

显然上述方程与方程(23)是等价的.选择初始近似y(t)=cos(t)，并且再次利用自由迭代公式(10)和数学工具Maple，可以得到二次迭代解：

y(t)=-0.501-2exp(-0.05t)sin3t+0.82exp(-0.05t)cost+
0.008 61exp(-0.1t)sint+0.16exp(-0.05t)sint-0.038sint+
0.004 3exp(-0.1t)sint-0.03exp(-0.015t)cost-
1.02exp(-0.035t)cost-0.25exp(-0.035t)sint+2.16cost+
0.040sint+0.006 1exp(-0.05t)sint+0.005exp(-0.1t)sint+
0.27exp(-0.1t)cost+0.003 9sin(3t)-0.001 8exp(-0.15t)sint-
0.002 5exp(-0.1t)sint+0.004 3exp(-0.1t)sin(3t)t-1.32exp(-0.05t)cost+
0.13exp(-0.1t)cost-0.002 1exp(-0.1t)sin(3t)+0.038exp(-0.05t)sint.

图4显示了二阶迭代解与参照解的逼近程度，从中可以看出，用SFIA方法得到的二阶迭代近似解与数值参照解非常接近.

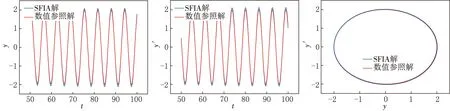
图4 例3 SFAI二阶近似解与数值参照解的比较

在上面得到的近似解中，没有形如tsint和tcost之类的长期项，但有exp(-βt)tsin(t)和exp(-βt)tcos(t)等项.注意到当时间t→∞时，项exp(-βt)tsin(t)和exp(-βt)tcos(t)趋于0.从而可以看出利用SFIA方法得到的二阶近似解没有长期项.

在上面的讨论中引入了正的阻尼项来避免长期项的出现，因为正的阻尼通常是消耗能量的，所以在相应的基本解矩阵中要包含类似于exp(-t)等项，从而可以有效地避免高阶近似中长期项的出现.

例4 考虑具有阻尼项的数学摆运动：

(26)

其中ε>0，ε≪1.

为了得到基本解矩阵，将系统(26)改写为

(27)

选择初始近似y(t)=exp(-t)，同样利用自由迭代公式(10)和数学工具Maple，可以得到一阶近似解

y(t)=0.903 8exp(-t)cos(1.41t)+0.96exp(-3t)+0.269exp(-t)sin(1.41t).

(28)

图5显示了SFIA方法得到的近似解和参照解之间具有很好的近似程度.

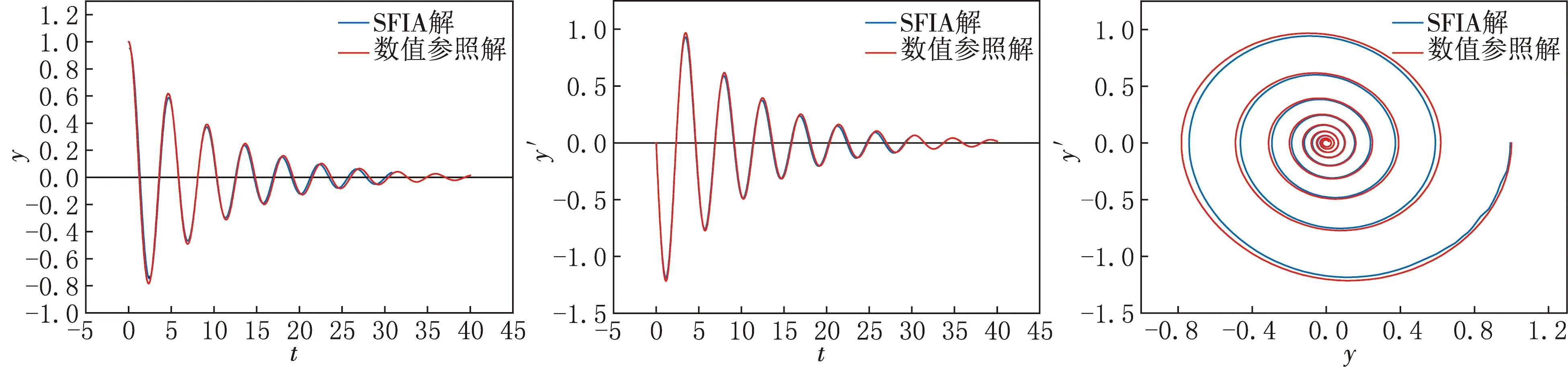
图5 例4 SFIA近似解与数值参照解的比较

注1 从上面的分析与模拟过程可以看出，系统中正的阻尼项将会有助于消去长期项，如果系统中没有正的阻尼项，可以构造合适的含有正的阻尼项的等价系统用来消除高阶近似中的长期项.

注2 初始近似值的选取是非常关键的，目前还没有一般的方法给出一个好的初始近似值.然而，线性系统的解通常可以作为初始近似解.

注3 如果系统中的参数不是常数，某些参数与时间相关，则不太容易得到基本解矩阵.在这种情况下，可以考虑构造一个所有系数均为常数的辅助系统来帮助得到合适的基本解矩阵.这一情况可以参照系统(24) .

3 结论

针对非线性系统的近似解问题，提出了一种离散SFIA.构造了不需要消去长期项的迭代过程，给出了SFIA收敛性的证明过程.重点研究了如何获得一些实用的机械和物理系统的近似解析解的技术.详细分析了二次非线性、三次非线性、Rayleith和数学摆系统的逼近过程，表明了系统的有效性.