对称群Sn(17≤n≤19)的一个新刻画①

李梦瑶， 杨国川， 晏燕雄

1.西南大学 数学与统计学院，重庆 400715； 2.208水文地质工程地质队，重庆 400700

本文涉及的群均为有限群．设G是有限群，

πe(G)={|x|：x∈G}

另外，mi(G)表示群G的第i高阶元素的阶，

m1(G)=max{|g|：g∈G}

Gp表示群G的一个Sylowp-子群．pα‖|G|表示pα||G|但pα+1|/|G|，其中α是非负整数．其他未说明的符号和术语都是标准的(见文献[1])．

众所周知，利用群的数量性质研究群结构一直是群论研究的热点，而如何用尽可能少的数量关系来刻画群的结构是群论研究中非常有意义的课题．群的阶和群中元素的阶 (简称两阶)是群的两个最基本的数量条件，这两个数量关系对群结构有着非常重要的影响．关于该问题，施武杰教授在20世纪80年代提出过如下猜想(这一猜想被列入文献[2]中)：

猜想设G为有限群，H为有限非交换单群，则G≅H当且仅当πe(G)=πe(H)且|G|=|H|．

该猜想被文献[3]最终证明．此后，许多群论学者尝试弱化两阶的条件来刻画群的结构．例如，文献[4-10]提出用群的阶以及最高阶元素的阶刻画有限单群，并成功刻画了散在单群、K3-单群、K4-单群、部分李型单群、部分交错群An(5≤n≤13)及对称群Sn(5≤n≤7)．文献[11]用群的阶以及最高阶元素的阶刻画了部分K5-单群．文献[12]证明了群G的同阶交换子群的个数之集为{1，3}等价于群G的同阶子群的个数之集为{1，3}．文献[13]讨论了与最高阶元素有关的几个数量条件对Conway单群和Fischer单群的结构的影响．文献[14]讨论了最高阶元素个数为6p2q的有限群．文献[15]用群的阶以及mi(G)(i=1，2，3)刻画了对称群Sn(8≤n≤15)．

本文将继续上述相关问题的研究， 研究群的某些特殊高阶元素的阶对群结构的影响，主要结果如下：

定理1设G是有限群，G≅S17当且仅当

(i) |G|=|S17|；

(ii)mi(G)=mi(S17)(i=1，2，3)．

定理2设G是有限群，G≅S18当且仅当

(i) |G|=|S18|；

(ii)mi(G)=mi(S18)(i=1,2,3,4)．

定理3设G是有限群，G≅S19当且仅当

(i) |G|=|S19|；

(ii)mi(G)=mi(S19)(i=1，2)．

定理1的证明

必要性显然，下面只证充分性．

由文献[16]得

|G|=215·36·53·72·11·13·17

m1(G)=210m2(G)=140m3(G)=120

步骤1 证明G有一个正规群列1◁_N◁M◁G，使得M/N为非交换单群，且11·17||M/N|．

设

G=G0▷_G1▷_ …▷_Gn-1▷_Gn=1

为G的主群列，则存在i，使得

π(Gi)∩{11，17}≠∅π(Gi+1)∩{11，17}=∅

设M=Gi，N=Gi+1，则G▷_M▷N▷_ 1为群G的正规列，且M/N为G/N的极小正规子群．

断言{11，17}⊆π(M)．若否，设11∉π(M)，17∈π(M)，则11∈π(G/M)．令

M17∈Syl17(M)G11∈Syl11(G)

则G11可共轭作用在M上．由文献[17]的引理8.3.1可知M中存在G11-不变的Sylow 17-子群M17， 则

|G11/CG11(M17)|||Aut(M17)| 11 ∈π(CG11(M17))

故187∈πe(G)，矛盾于m2(G)=140．于是11 ∈π(M)．

同理可证，不存在11 ∈π(M)，且17∉π(M)．因此{11，17}⊆π(M)．

下证M/N为非交换单群．

因为

{11，17}⊆π(M)π(N)∩{11，17}=Ø

故

{11，17}⊆π(M/N)

M/N为G/N的极小正规子群，且17|||G|，故M/N必为非交换单群，且11·17||M/N|．

步骤2 证明M/N≅A17．

由步骤1知M/N为非交换单群，|M/N|||S17|且11·17||M/N|，

|G|=215·36·53·72·11·13·17

由文献[16]知M/N≅A17．

步骤3 证明G≅S17．

若M/N≅A17，由文献[15]的引理2知G中存在正规子群C，使得

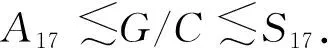
若|C|=2，则G/C≅A17．故G≅2×A17，或G≅2·A17，则m3(G)=126．这与m3(G)=120相矛盾．

若|C|=1，则G/C≅S17，即G≅S17．

综上所述，定理1得证．

定理2的证明

必要性显然，下面只证充分性．

由条件知

|G|=216·38·53·72·11·13·17

m1(G)=210m2(G)=180m3(G)=168m4(G)=140

类似于定理1的证明可以得到，G有一个正规群列1◁_N◁M◁_G，使得M/N为非交换单群，且11·17||M/N|．由文献[16]知M/N≅A17，A18．

1 charD1charD2char … charDn=C

使得Di/Di-1为初等交换群，其中Di-1为Di的极大正规子群．从而一定存在i，使得|Di/Di-1|=3，32．于是

则

|G/Di-1/CG/Di-1(Di/Di-1)|||Aut(Di/Di-1)|

由

G/C≅G/Di-1/C/Di-1

可得G/Di-1包含A17这个截断．由A17有55阶元，且

|G/Di-1/CG/Di-1(Di/Di-1)|||Aut(Di/Di-1)|

可得CG/Di-1(Di/Di-1)有55阶元．故G有165阶元，这与m4(G)=140矛盾．

若M/N≅A18，由文献[15]的引理2知，存在C◁_G使得

如果|C|=2，则G/C≅A18，从而G≅2×A18，2·A18，这时m4(G)=154，矛盾．

如果|C|=1，则G/C≅S18，即G≅S18．

综上所述，定理2得证．

定理3的证明

必要性是显然的，下面只证充分性．

已知

|G|=216·38·53·72·11·13·17·19

m1(G)=420m2(G)=210

类似于定理1的推理知，G有一个正规群列1◁_N◁M◁_G，使得M/N为非交换单群，且17·19||M/N|，其中19=max{p：p∈π(M/N)}，由文献[16]知，M/N≅A19，J3．

若M/N≅J3，由文献[15]的引理2知，存在G的正规子群C，使得

从而

|C|=29·33·52·72·11·13

或

|C|=28·33·52·72·11·13

令

C13∈Syl13(C)G19∈Syl19(G)

从而G19可共轭作用在C上．由文献[17]的引理8.3.1可知C中存在G19-不变的Sylow 13-子群C13，则

|G19/CG19(C13)|||Aut(C13)| 19 ∈π(CG19(C13))

故247∈πe(G)，这与m2(G)=210矛盾，故M/NJ3，于是M/N≅A19．由文献[15]的引理2可知，G中存在正规子群C，使得

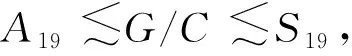
如果|C|=2，则G/C≅A19．故G≅2×A19，2·A19，从而m2(G)=330，这与m2(G)=210相矛盾．

如果|C|=1，则G≅S19．

综上所述，定理3得证．

注定理1中的m3(G)不能缺少，否则G≅2×A17，2·A17； 定理2中的m3(G)与m4(G)不能缺少，否则G≅2×A18，2·A18．