具有时滞效应的SIS模型的动力学分析①
刘志华, 曹慧, 徐河苗
1.陕西科技大学 数学与数据科学学院,西安 710029; 2.长治学院 数学系,山西 长治 046011

1 模型的建立
以流感背景,并基于经典的SIS传染病模型,将媒体报道的染病人数对疾病发生率的影响用函数e-αI(t-τ)来刻画,建立如下的模型:
(1)
其中:S(t)和I(t)分别表示t时刻的易感染者和染病者人数,Λ表示易感者的常数输入率,μ表示自然死亡率,γ表示染病者的恢复率.
2 模型的适定性与平衡点
在本节中,我们将先分析模型(1)的解的非负性和有界性,再借助极限系统理论给出平衡点的存在性.

事实上,由模型(1)中的第二个方程直接计算可得
显然,I(t)≥0,t∈(0,τ]. 进而,类似计算得
以上分析说明,对于任意非负初值,必有I(t)≥0,t≥0成立.
下面说明S(t)≥0,t≥0成立. 假设∃t1>0,使得S(t)>0,t∈(0,t1),S(t1)=0,且S(t)>0,t>t1. 则有
与S(t)<0,t>t1矛盾. 也就是假设不成立. 即S(t)≥0,t≥0成立.
以上分析说明,模型(1)中任意具有非负初值的解一定是非负的. 下面来说明模型(1)解的有界性.将模型(1)中的两个方程相加可得

(2)
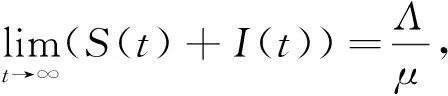
另外,利用再生矩阵的办法[15]可以得到模型(1)的基本再生数为
将S(t)=N*-I(t)代入模型(1),可得模型(1)的极限模型
(3)
利用极限系统理论可知[16],模型(3)与模型(1)有相同的动力学性态. 接下来的研究将借助模型(3)来分析模型(1)的动力学性态.
(4)
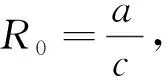
显然,模型(4)始终有零平衡点X0=0. 为了找到模型(4)的正平衡点X*,令
f(X)=ae-bX(1-X) ,X∈[0, 1]
通过直接计算可得:f(0)=a,f(1)=0,且f′(X)<0,这说明a>c时,也就是,当R0>1时,模型(4)存在唯一的正平衡点X*,满足ae-bX*(1-X*)=c.即下面的定理成立:
定理1模型(4)始终存在零平衡点X0=0,并且当R0>1时,模型(4)还存在唯一的正平衡点X*,满足ae-bX*(1-X*)=c.
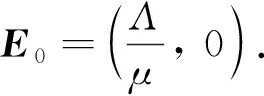
下面研究模型(4)的零平衡点和正平衡点的稳定性.
定理2如果R0<1,模型(4)的零平衡点X0是全局渐近稳定的; 如果R0>1,X0是不稳定的.
证直接计算可得,模型(4)在X0=0处的特征方程为
λ-a+c=0
(5)
即λ=c(R0-1). 由Hurwitz判据可知,若R0<1,有λ<0,即模型(4)的零平衡点是局部渐近稳定的.若R0>1,则λ>0,这说明模型(4)的零平衡点是不稳定的.
下面来证明零平衡点的全局稳定性. 记V1(t)=X(t),则
(6)
显然,当R0<1时,V′1|(4)<0,故模型(4)的零平衡点是全局渐近稳定的. 证毕.
定理3如果R0>1,τ=0,那么模型(4)的正平衡点X*是全局渐近稳定的.
证直接计算可知,模型(4)在X=X*处的特征方程为
(7)
当τ=0时,特征方程(7)可重新写为
(8)
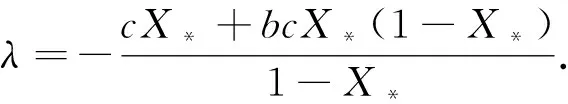
(9)
由于y=e-bX是一个递减函数,因此,有(X-X*)(e-bX-e-bX*)<0成立. 也就是,V′2|(4)≤0. 另外,当且仅当X=X*时,V′2|(4)=0. 这说明M={X|V′2(x)=0}={X*},也就是,模型(4)在M上的最大不变集就是{X*}.根据LaSsalle不变集原理可知,当R0>1时,模型(4)的正平衡点X*是全局渐近稳定的. 证毕.
由定理2和定理3可知,当R0<1时,模型(1)的无病平衡点E0和地方病平衡点E*是全局渐近稳定的.
3 Hopf分支
在本小节中将讨论τ>0时,模型(4)可能发生的Hopf分支. 为此,假设λ=iω,ω>0,代入方程(7)可得
(10)
进而有
(11)
也即
(12)
如果方程(12)有一个正根ω0,则正平衡点X*的稳定性可能会随着τ的改变而改变. 为此,记c*=e-bX*,则当b>1且c*>e1-b时,方程(12)存在一个正根
(13)
进而可得
(14)
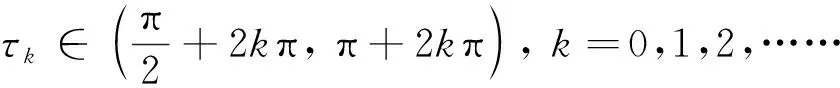
因此,

(15)

利用泛函微分方程的Hopf分支理论[17],得到下面的结论.
定理4假设R0>1,
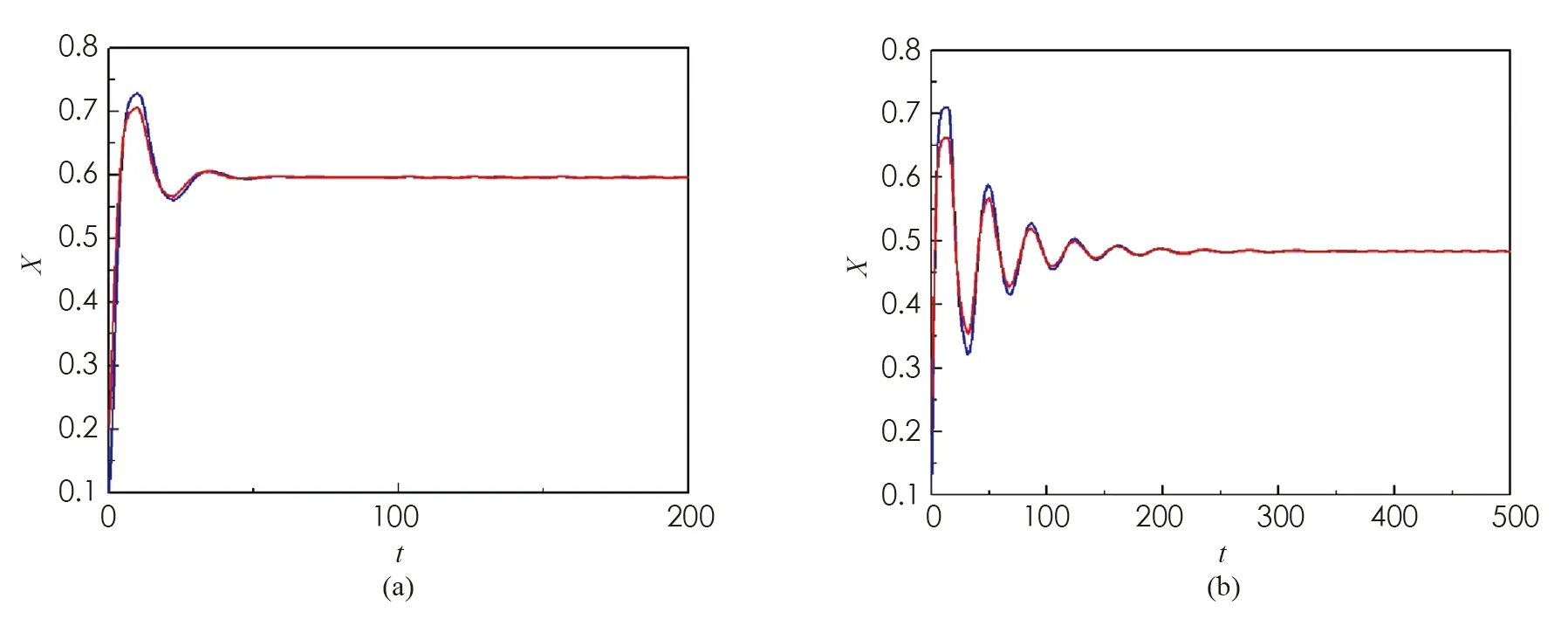
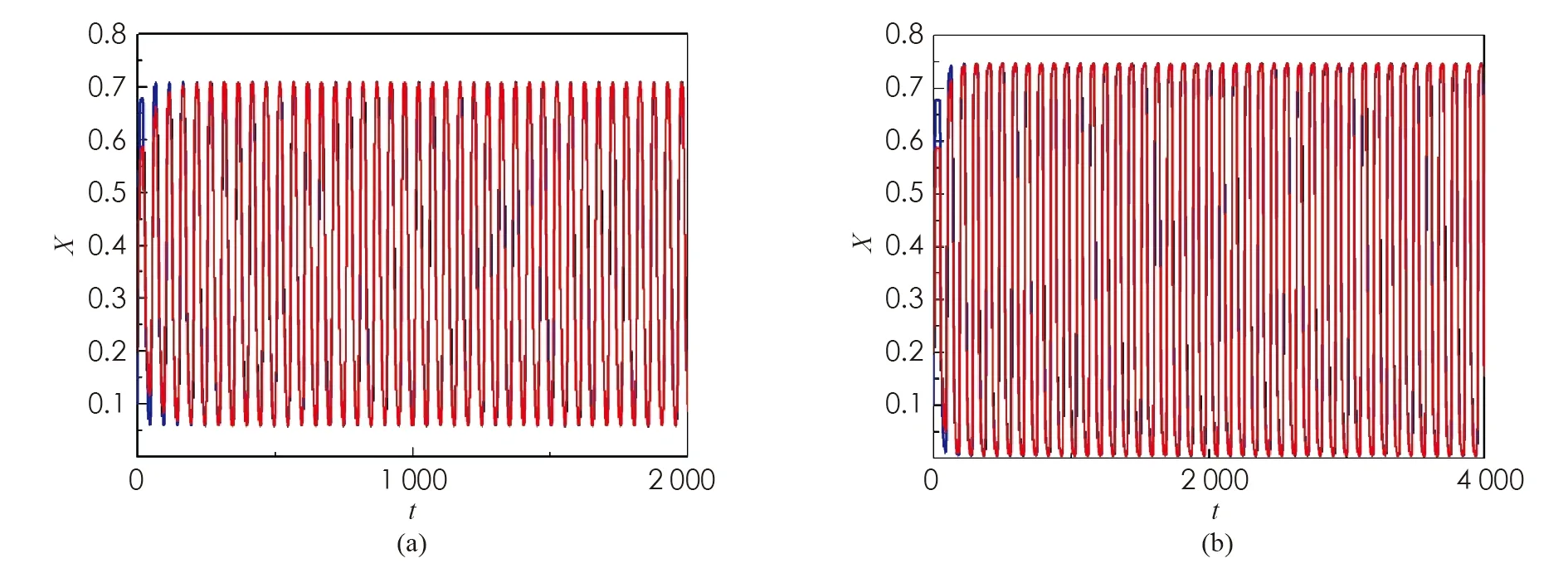
(1) 若0 (2) 若b>1,c*≤e1-b,则对任意τ≥0,模型(4)的正平衡点X*是渐近稳定的; (3) 若b>1,c*>e1-b,则对任意τ∈[0,τ0],模型(4)的正平衡点X*是渐近稳定的; (4) 若b>1,c*>e1-b,则对任意τ≥τ0,正平衡点X*是渐近稳定的; 且在τ=τk,k=0,1,2…时,模型(4)会在X*处发生Hopf分支. 在本小节中,将利用文献[18-19]中的全局Hopf分支理论来讨论模型(4)产生的局部Hopf分支的全局延拓问题. 为此,引入变换y(t)=x(τt),模型(4)可被改写为 y′(t)=F(yt,τ,T)F(yt,τ,T)∈X×R×R+ (16) 这里yt(θ)=y(t+θ),θ∈[-1,0],yt∈X,X=C([-1,0],T),并且 y′(t)=τae-by(t-1)(1-y(t))y(t)-τcy(t) (17) 引入下面的记号: ∑=Cl{(y,τ,T):y是方程(17)的T周期解}∈X×R×R+ 引理1方程(17)的所有周期解是一致有界的. 证设y(t)是方程(17)的一个非平凡的周期解,且令y(t1)=N和y(t2)=n分别为其最大值和最小值,满足0 ((1-N)ae-by(t1-1)-c)N=0 (18) ((1-n)ae-by(t2-1)-c)n=0 (19) 引理2如果b>1,且c*>e1-b满足,方程(17)没有周期为1或2的周期解[19]. 证方程(17)的任意非平凡的周期为1周期解为u(t),且为如下常微分方程的非平凡周期解: u′(t)=τ(ae-bu(1-u-c))u (20) 由于一阶纯量常微分方程不存在非平凡周期解,故(20)式不存在周期解. 若(17)式有周期为2的非平凡周期解u(t),则u1(t)=u(t),u2(t)=u(t-1),并且满足 (21) 由(21)式与y(t)相对应的周期轨道包含在如下区域: 则对所有的(u1,u2)∈G1总存在 因此由Bendixson周期解不存在准则[20]知(21)式没有平凡周期解. 证毕. 证设y(t)为方程(17)的周期为4的周期解,并令ui(t)=y(t-i+1),i=1,2,3,4. 于是u(t)=(u1(t),u2(t),u3(t),u4(t))是下述常微分方程的周期: (22) 由引理1可知(22)式与y(t)相对应的周期轨道包含在如下区域: (23) 解的一致有界性表明所有周期解均位于G2内,为了说明方程(17)没有4的周期解,只需证明方程(17)在区域G2中不存在周期解即可. 那么为证明方程(17)在区域G2中不存在周期解,我们将应用高维常微分方程Bendixson准则[20]得到方程(22)右端的Jacobi矩阵为 (24) 这里记Ai=c-a(1-2ui)e-bui+1,Bi=abui(1-ui)e-bui+1,u5=u1,i=1,2,3,4. 下面对R6选取向量模: 其中(i,j)∈{(1,4),(2,1),(3,2),(4,3)},(p,q)∈{(1,3),(2,4)}. 要使μ(J[2](u))<0,当且仅当对所有u∈G2,使得 (25) (26) 进一步有 因此,应用文献[20]中的推论3.5可得方程组(22)不存在周期为4的周期解. 证毕. 定理51) 如果R0>1,b>1,且c*>e1-b,则对任意τ>τ1,方程(17)至少有一个非平凡的周期解. 对τ∈[τk-δk,τk+δk]成立,且 Ωεk={(u,T)|0 所以, 在本小节中,将借助数值模拟来验证所得理论结果的合理性. 为此,令a=1.2,c=0.3. 下面分情况讨论. 当b=0.8<1,τ=10时,如图1(a)所示,模型(4)从不同初值出发的解最终都趋近于正平衡点X*,这说明X*是稳定的. 当b=1.5>1时,直接计算得e1-b=0.606 5>c*. 令τ=15,则X*仍是稳定的,见图1(b). 图1 b=0.8,τ=10时模型(4)平衡点X*的稳定性 当b=2.5>1时,e1-b=0.223 1 图2 b=2.5,τ=8时模型(4)平衡点X*的稳定性 下面展示平衡点X*处的Hopf分支的全局延拓性. 此时令a=1.2,b=2.5,c=0.3,相应地,平衡点X*=0.369 8,R0=4>1,c*=0.396 7.通过(13)和(14)式计算得τ0=8.517 9,τ1=37.833 8. 当b=2.5,并且分别满足定理5的条件1)和2)时,各自选取τ=40>τ1,τ=20>τ0,如图3(a),(b)所示,两张图都展示了在平衡点X*附近从τ0分支出的周期解是大范围存在的. 图3 模型(4)在平衡点X*处的大范围周期解 相应地, 随着时滞τ的不断增加,模型(4)在平衡点X*处展现出了Hopf分支(图4). 图4 系统(4)在平衡点X*处的Hopf分支图 在本小节中,主要研究了媒体报道的染病者数量对SIS模型动力学性态的影响. 给出了模型(1)的基本再生数,借助极限系统,讨论了系统(4)平衡点的存在性、稳定性,以及平衡点不稳定时可能发生的Hopf分支. 当R0<1时,模型(1)存在全局渐近稳定的无病平衡点; 而当R0>1时,模型(1)存在唯一的地方病平衡点, 并且地方病平衡点的稳定性会随着时滞τ的增加而发生改变,即:在τ=0的情况下,地方病平衡点是全局渐近稳定的; 当τ>τ0时,地方病平衡点不再稳定,并会发生全局延拓的Hopf分支.我们也给出了发生全局Hopf分支延拓的条件. 系统(4)中的参数b=αN*,通过改变b的参数值大小,可以明显看出b值对平衡点的影响.也就是说, 由媒体报道的染病者数量所引起的时滞效应会使得模型的动力学性态更加丰富. 即媒体报道引起的时滞效应会改变地方病平衡点的稳定性,产生全局Hopf分支.3.1 全局Hopf分支的存在性

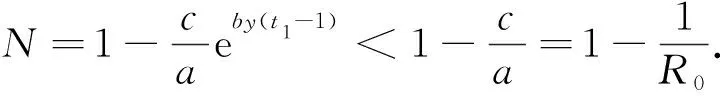
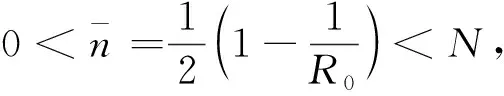

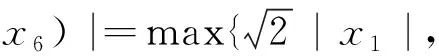


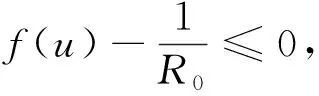

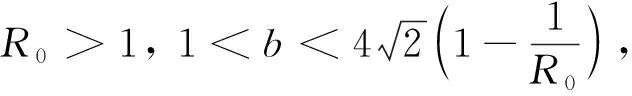
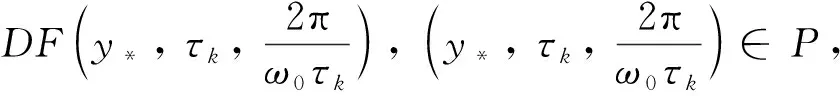

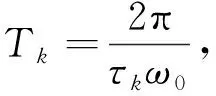
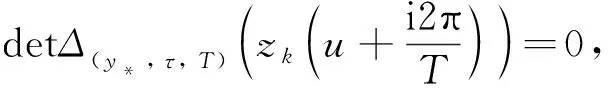
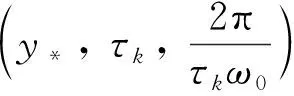
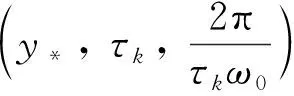
4 数值模拟


5 总结

