用循环子群的个数刻画单群A5①

2022-09-27 12:53林子靖仝巍周伟

西南师范大学学报（自然科学版） 2022年9期

关键词：子群同理个数

林子靖，仝巍，周伟

西南大学数学与统计学院，重庆400715

对有限群G，用c(G)表示G的循环子群的个数[1]．循环子群的个数对于群的结构是有一定影响的．显然c(G)=|G|当且仅当G是初等Abel 2-群．文献[2-6]分类了|G|-c(G)≤5的群．

文献[2]证明了c(G)=|G|-1当且仅当G≅C3，C4，S3，D8．

文献[3]证明了c(G)=|G|-2当且仅当G≅C6，C2×C4，D12，C2×D8．

文献[4]证明了c(G)=|G|-3当且仅当G≅Q8，C5，D10．

文献[6]证明了c(G)=|G|-5当且仅当G≅C7，D14，C3×|C4．

文献[7]证明了对任意有限群G，有|G|≤8(|G|-c(G))，并分类了1≤ |G|-c(G)≤32的群结构．

还有很多学者用交换子群的个数和最高阶元的个数来研究群的结构，参见文献[8-11]．

本文证明了G≅A5当且仅当|G|=60，且c(G)=32．

引理1[1]设G是有限群，若G=G1×G2×…×Gn，其中(|Gi|， |Gj|)=1，i≠j，则

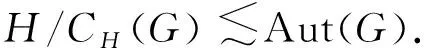
本文所涉及的群都是有限群，所用符号都是标准的．

引理5若|G|=p2qr，其中p，q，r是不同的素数，则G是可解群或60阶交错群A5．

证设G不可解．若G非单，则G有非平凡正规子群N，

|N|∈{p，p2，q，r，pq，pr，qr，p2q，p2r，pqr}

|G/N|∈{p，p2，q，r，pq，pr，qr，p2q，p2r，pqr}

从而N和G/N可解，G可解，矛盾．故G是单群．由于|G|的最小质因子不含3次方，则12||G|，所以

p=2q=3r≥5 1+kr|12

从而有r=5或r=11．如果r=11，由于G是单群，所以G有12个Sylow 11-子群，从而有120个11阶元．G至少有4个Sylow 3-子群，所以至少有8个3阶元，且

|G|=22×3×11=132

所以G只有1个Sylow 2-子群，矛盾．故

r=5 |G|=60

又因G是单群，由文献[16]，有G≅A5．

定理1G≅A5当且仅当|G|=60，且c(G)=32．

证充分性显然，下证必要性．

由引理5知，只需证G不可解．

假设G可解．则G有极小正规子群N，且N为初等Abelp-群．因为

|G|=60=22·3·5

所以|N|∈{2，3，4，5}．设P2∈Syl2(G)，P3∈Syl3(G)，P5∈Syl5(G)．

下证G的Sylow 5-子群正规．由Sylow定理知，G有1个或6个Sylow 5-子群．若G有6个Sylow 5-子群，则|N|≠5，从而|N|∈{2，3，4}．

如果|N|=3，则G有3-补，设为H1，|H1|=20．H1中有1个Sylow 5-子群，所以P5◁_H1．从而

H1≤NG(P5) |G∶NG(P5)|≤|G∶H1|≤3

即G的Sylow 5-子群个数为1，矛盾．

如果|N|=4，同理，矛盾于G的Sylow 5-子群的个数为6．

如果|N|=2，则G有2-补，设为H2，|H2|=30．

由Sylow定理知H2中有1个或6个Sylow 5-子群．若H2中有6个Sylow 5-子群，则H2中有24个5阶元．又由Sylow定理知H2中有1个或10个Sylow 3-子群．若H2中有1个Sylow 3-子群，令P5作用在P3上知，P5与P3可交换，所以P3P5≤G，即G中有15阶循环子群． 15阶循环子群的生成元个数为8，所以H2中至少有8个15阶元．从而|H2|≥33，矛盾．若H2有10个Sylow 3-子群，则H2中有20个3阶元，所以|H2|≥45，矛盾．从而任一30阶群中只有1个Sylow 5-子群，即P5◁_H2．所以

H2≤NG(P5) |G∶NG(P5)|≤|G∶H2|≤2

矛盾．综上所述，G只有1个Sylow 5-子群，即P5◁_G．

下证G的Sylow 3-子群正规．由P5◁_G知，P3P5≤G，即G中存在15阶循环子群，且对G的任一15阶循环子群H，都有P5◁_H．|G/P5|=12，所以H/P5是G/P5的Sylow 3-子群．由Sylow定理知，G有1个、 4个或10个Sylow 3-子群．

若G有10个Sylow 3-子群，则G/P5中有10个Sylow 3-子群．根据引理4，G中有10个15阶循环子群，从而有80个15阶元，矛盾于|G|=60．

若G中有4个Sylow 3-子群，同理G/P5中有4个Sylow 3-子群．由引理4，G中有4个15阶循环子群，从而有32个15阶元．令M是G中1阶元、3阶元、5阶元、15阶元之集合，则|M|=45，且对∀x∈GM，有φ(o(x))≥1，所以

由引理2，

由条件c(G)=32，矛盾．从而G只有1个Sylow 3-子群，即P3◁_G．

由G可解知，G的所有Hall子群共轭．因为P3P5是G的Hall子群，且

P3P5=P3×P5◁_G

所以G中只有1个15阶循环子群．下面用nk表示G的k阶循环子群的个数．因此

n1=1n3=1n5=1n15=1

显然

则

60=n1+n2+2n3+2n4+4n5+2n6+4n10+4n12+8n15+8n20+8n30+16n60

32=n1+n2+n3+n4+n5+n6+n10+n12+n15+n20+n30+n60

若n60=1，则G为循环群，c(G)=12，矛盾．从而

n4+n6+3n10+3n12+7n20+7n30=17

(1)

下面继续讨论G的Sylow 2-子群的个数．

情形1G有1个Sylow 2-子群．

若P2=C4，则G=C4×C3×C5=C60为循环群，c(G)=12，矛盾．

若P2=C2×C2，则

G=C2×C2×C3×C5

由引理1知

则c(G)=16，矛盾．

情形2G有3个Sylow 2-子群．

若P2=C4，则n4=3，从而G中至多有3个2阶元，即n2≤3．令M是G中1阶元、2阶元、3阶元、4阶元、5阶元、15阶元之集合．若n2=3，则|M|=24，且对∀x∈GM，有

o(x)≥6φ(o(x))≥2

所以

从而由引理2，c(G)≤28，矛盾于c(G)=32．若n2=1，则|M|=22，同理，c(G)≤27，矛盾．

若P2=C2×C2，则n4=0，G中至多有9个2阶元．

令M是G中1阶元、2阶元、3阶元、5阶元、15阶元之集合．同理，有c(G)≤31，矛盾．

情形3G有5个Sylow 2-子群．

若P2=C4，则n4=5，从而G中有10个4阶元，至多5个2阶元，即n2≤5．令M是G中1阶元、2阶元、3阶元、4阶元、5阶元、15阶元之集合．若n2=5，则|M|=30，且对∀x∈GM，有

o(x)≥6φ(o(x))≥2

从而由引理2知，c(G)≤29，矛盾．同理，若n2=3，则|M|=28，从而c(G)≤28，矛盾．若n2=1，则c(G)≤27，矛盾．

若P2=C2×C2，则n4=0．因为

P3◁_GP5◁_G

所以

P3P5◁_GP3P5=C15

从而

所以i，j∈{1，4，11，14}．由G非交换，则i，j不能同时为1．从而G有以下4种类型：

G1=〈a，b，c：a2=b2=c15=1，ab=ba，ca=c4，cb=c4〉c(G1)=28

G2=〈a，b，c：a2=b2=c15=1，ab=ba，ca=c11，cb=c11〉c(G2)=20

G3=〈a，b，c：a2=b2=c15=1，ab=ba，ca=c14，cb=c14〉c(G3)=38

G4=〈a，b，c：a2=b2=c15=1，ab=ba，ca=c4，cb=c11〉c(G4)=35

矛盾．

情形4G有15个Sylow 2-子群．

若P2=C4，则n4=15，所以|NG(P2)|=4，从而P2=NG(P2)．由(1)式有

n6+3n10+3n12+7n20+7n30=2

故

n6=2n10=n12=n20=n30=0

令

P2=〈a〉P3=〈b〉

因为n12=0，即G中没有12阶元，所以P2作用在P3上非平凡，从而

P2P3=〈a，b：a4=b3=1，ba=b-1〉

|G/P3|=20P5◁_G

所以

G/P3=〈a，c：a4=c5=1，ca=ci，i4≡1(mod 5)〉

因为G中没有20阶元，所以P2作用在P5上非平凡，从而i=2，3，4．

若i=2，则

G/P3=〈a，c：a4=c5=1，ca=c2〉

此时G/P3中有5个2阶元，从而有5个2阶循环子群．设K/P3=〈x〉是G/P3的任一2阶循环子群．因为P2在P3上的作用为逆变换，即ba=b-1，x是P2中的2阶元，x=a2，所以bx=ba2=b，即〈x〉作用在P3上平凡．从而

K=P3×〈x〉=C6

由于G/P3中有5个2 阶循环子群，所以G中至少有5个6阶循环子群，矛盾于n6=2．

若i=3，同理，矛盾．

若i=4，则

G/P3=〈a，c：a4=c5=1，ca=c4〉

此时G/P3中有10阶元，从而有10阶循环子群．设J/P3=〈y〉是G/P3的任一10阶循环子群．则|J|=30．由30阶群分类知，矛盾．若P2=C2×C2，与情形3同理，矛盾．

综上所述，G不可解．由引理5，G≅A5．