鲁棒最小二乘孪生支持向量机及其稀疏算法

靳启帆，陈 丽，2，徐明亮，姜晓恒

1.郑州大学 计算机与人工智能学院，郑州450001

2.郑州大学 体育学院（校本部），郑州450001

支持向量机（support vector machine，SVM）[1]是一种基于结构风险最小化和最大间隔法原理的监督学习方法。SVM通过求解一个凸二次规划问题得到划分两类点的决策超平面，而凸二次规划问题的求解计算复杂度较高，导致SVM 训练速度较慢。为克服这一问题，Jayadeva等[2]提出了孪生支持向量机（twin support vector machine，TSVM）。TSVM 旨在寻找两个非平行的投影超平面，使每一个超平面尽可能靠近一类样本点并且远离另一类样本点。与SVM 相比，TSVM 只需求解两个规模更小的二次规划问题。对于平衡数据集，采用线性核的TSVM 计算复杂度仅为SVM 的1/4。为进一步提高TSVM的运算速度，Kumar和Gopal[3]基于最小二乘损失函数提出了最小二乘孪生支持向量机（least squares twin support vector machine，LSTSVM），LSTSVM 将TSVM中的不等式约束用等式约束替代，通过求解两个线性规划来代替求解复杂的二次规划问题。与TSVM相比，LSTSVM具有计算简单和训练速度快的优势。然而，由于LSTSVM采用的是最小二乘损失函数，一方面其损失值随误差值的增大而无限增大，导致具有较大误差值的异常点对投影超平面的构造影响较大，因此LSTSVM对异常点较敏感。另一方面，已有求解LSTSVM的算法得到的解中几乎所有的训练样本都是支持向量，即解缺乏稀疏性，而对于大规模数据，并不是所有的样本点都对模型的建立起到关键的决策作用。针对以上两个问题，本文提出了一种鲁棒最小二乘孪生支持向量机模型，并得到了其稀疏解。

克服模型对异常点敏感的常用方法可分为三类：一类是在模型中加入权重，Chen等[4]提出了加权最小二乘孪生支持向量机（weighted LSTSVM，W-LSTSVM），通过对样本增加不同的权重，以提高算法的鲁棒性，但是W-LSTSVM 对于每一个模型，仅对其中一类数据加权重，这使得W-LSTSVM 对于含有交叉噪声的数据集分类效果不好。针对这一问题，储茂祥等[5]提出了广泛权重的最小二乘孪生支持向量机（widely weighted least squares twin support vector machine，WWL-STSVM），WWL-STSVM 对于每个模型，在正负两类样本上都增加权重，很好地抑制了交叉噪声对分类效果的影响。另一类方法是采用估计值代替异常点处的值，黄贤源等[6]利用局部样本中心距离对训练样本进行异常点检测，然后用异常点的平面坐标推导的估计值来代替异常点处的值。郭战坤等[7]提出了一种基于局部异常因子（local outlier factor，LOF）和奇异谱分析（singular spectrum analysis，SSA）的LOF-SSA-LSSVM预测模型，采用LOF算法进行异常点检测，确定异常数据的位置，最后通过插值法或应用LSSVM中的预测值来修正原始序列中的异常点的值。第三类方法是利用非凸损失函数来提高模型的鲁棒性。Shen 等[8]和Wu 等[9]基于截断Hinge 损失函数提出鲁棒SVM 模型。Wang 等[10]和Yang 等[11]基于截断最小二乘损失函数提出鲁棒LSSVM（robust LSSVM，R-LSSVM）模型。安亚利等[12]提出了一种推广的指数鲁棒最小二乘支持向量机模型。实验结果表明基于非凸损失函数的方法可有效抑制异常点对模型分类精度的影响。

增强解的稀疏性方面，常用方法是减枝法。Suykens等[13]通过去除Lagrange乘子相对较小的支持向量来提升算法的稀疏性。Zeng 等[14]通过移除在对偶空间里对目标函数作用较小的样本点来提高算法的稀疏性。Li等[15]提出通过将yi f(xi)的值较大的样本点移除来达到稀疏的目的。然而，这类方法需要迭代地求解一组线性方程组，虽得到了稀疏解，但增加了算法复杂性，降低了训练速度。刘小茂等[16]基于中心距离比值及增量学习的思想提出了一种基于预选支持向量的稀疏最小二乘支持向量机，该方法预先选取训练样本集的子集训练模型，加快了LSTSVM的训练速度，然而当所选子集不能代表原始样本集特性时，会影响学习的效果。Jiao等[17]提出快速稀疏近似LSSVM（fast sparse approximation LSSVM，FSA-LSSVM），该方法通过从基于核的字典中逐个添加基函数来迭代地构造近似决策函数，直到满足停止条件。De等[18]提出固定大小LSSVM（fixed-size LSSVM，FS-LSSVM），该算法先固定一些向量作为支持向量，然后计算训练样本的Rényi二阶熵，根据计算出来的Rényi二阶熵的大小来选择支持向量，然而该方法在迭代过程中，样本的熵不是在整个数据集中选择，而是仅在工作集中选择，这可能导致次最优解。Zhou 等[19]基于核矩阵不完全选主元Cholesky 分解提出了基于主元Cholesky的原空间LSSVM（pivoting cholesky of primal LSSVM，PCP-LSSVM）算法，该算法与已有LSSVM 算法相比，在保持分类准确率的同时提高了收敛速度。

针对LSTSVM 对异常点敏感和解缺乏稀疏性问题，本文基于截断最小二乘损失函数提出鲁棒最小二乘孪生支持向量机模型（robust LSTSVM，R-LSTSVM），并从加权的角度解释了R-LSTSVM 具有鲁棒性，为得到R-LSTSVM 的稀疏解，将R-LSTSVM 首先表示成两个凸函数的差，然后利用表示定理、DCA（difference of convex algorithm）方法和不完全Cholesky 分解提出了稀疏R-LSTSVM算法（sparse R-LSTSVM，SR-LSTSVM）。新算法可抑制异常点对模型的影响，并选取对模型建立有效的数据样本点，适合处理带异常点的大规模数据。

1 相关算法

1.1 最小二乘孪生支持向量机及相关算法

记训练样本集为T={(x1,y1),(x2,y2),…,(xm,ym)}，其中xi∈ℜd为训练样本，yi∈{+1,-1} 为样本的类别标签。设A∈表示标签为+1 的样本组成的矩阵，B∈表示标签为-1 的样本组成的矩阵，ℜm×d表示所有样本组成的矩阵，则线性LSTSVM 模型如下：

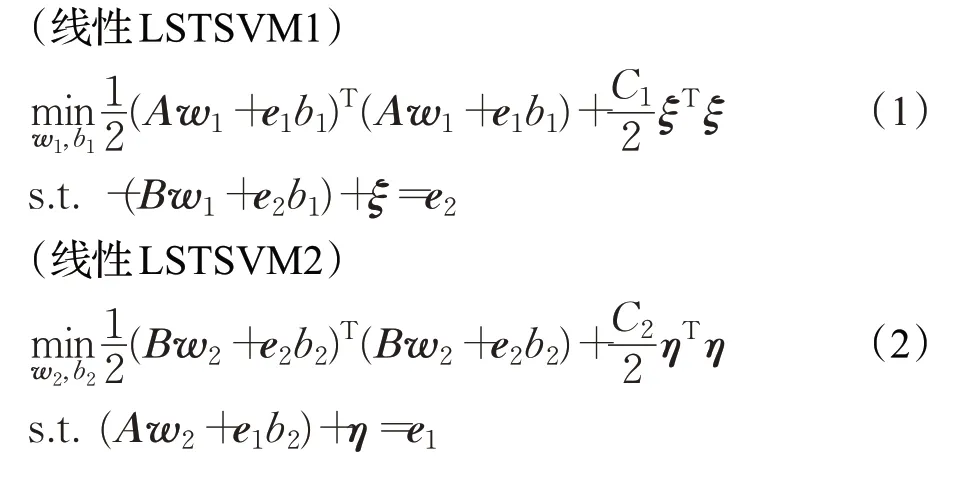
其中，e1∈，e2∈为元素全为1 的向量，ξ和η表示误差，C1和C2为惩罚因子。模型（1）、（2）的第一项表示使一类训练样本点尽可能靠近一个超平面，第二项表示最小二乘损失函数。由Lagrange 乘数法可得到线性LSTSVM的解为：

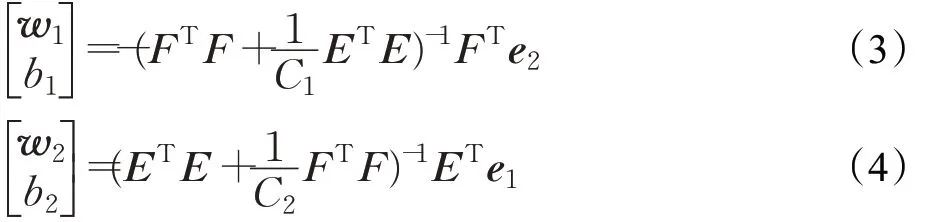
其中，E=[A e1],F=[B e2] 。由求到的w1、b1和w2、b2可得到两个非平行的投影超平面为xTw1+b1=0 和xTw2+b2=0。对于未知标签的样本x，根据样本点离超平面的距离来判断样本点的标签，即f(x)=

对于非线性情况，LSTSVM通过引入核函数K(xi,xj)=ϕ(xi)Tϕ(xj)，其中ϕ(x)是将x投影到高维特征空间的映射，得到非线性LSTSVM模型为：

（非线性LSTSVM1）

（非线性LSTSVM2）

其中，KAM=K(xi,xj)(xi∈A,xj∈M)，KBM=K(xi,xj)(xi∈B,xj∈M)，KMM=K(xi,xj)(xi∈M,xj∈M) 。由Lagrange乘数法可得到非线性LSTSVM的解为：

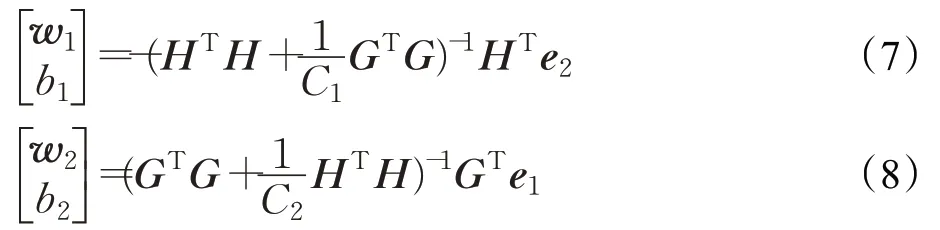
其中，H=[KAM e1]，G=[KBM e2] 。与线性LSTSVM投影超平面的构造类似，非线性LSTSVM的两个非平行的投影超平面为K(xT,MT)w1+b1=0 和K(xT,MT)w2+b2=0。对应的判别函数为：

通过式（7）、（8）得到的非线性LSTSVM 的解是稠密的，其计算复杂度为O(m3)。

1.2 不完全Cholesky分解方法

不完全Cholesky分解算法的时间复杂度为O(mr2)，其只需要计算核矩阵的至多r列(r≪m)及对角线上的所有元素就可以得到迹范数意义下核矩阵K的最优Nyström低秩近似PPT[19]。

2 稀疏鲁棒最小二乘孪生支持向量机

由于LSTSVM采用的是最小二乘损失函数Lsq(ξ)=ξ2，损失值随误差值ξ的增大而无限增大，因此LSTSVM对于误差值较大的异常点较敏感。为解决这一问题，本文采用截断最小二乘损失函数来降低异常点对超平面的影响，提出鲁棒LSTSVM 模型（R-LSTSVM），并从加权的角度解释了R-LSTSVM的鲁棒性。为使R-LSTSVM可处理大规模数据，本文基于表示定理、DCA 方法及不完全Cholesky 分解得到稀疏R-LSTSVM 算法（SRLSTSVM）。

2.1 鲁棒最小二乘孪生支持向量机模型

为克服LSTSVM 对异常点敏感的缺陷，本文基于截断最小二乘损失函数提出如下非线性鲁棒LSTSVM模型：

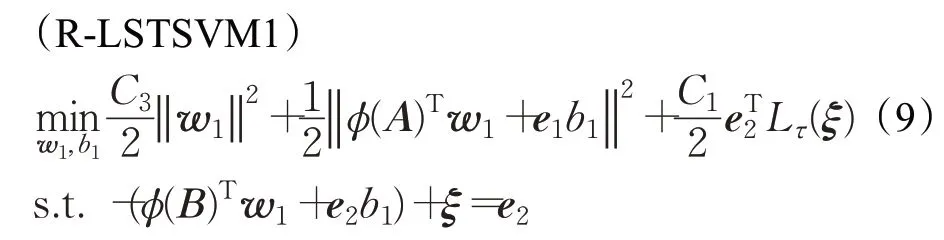
其中，模型（9）中目标函数的第一项为正则项，表示最大化投影超平面ϕ(x)Tw1+b1=0 和单侧边界超平面ϕ(x)Tw1+b1=-1 之间的距离，从而使模型式（9）的结构风险最小。式（10）中的目标函数的第一项也为正则项，其可使模型（10）的结构风险最小，C3和C4为正则化参数。采用的截断最小二乘损失函数Lτ(ξ)为：

其中，τ>0 为截断参数，图1给出了当τ=1.8 时Lτ(ξ)的图像，从图中可以看出当 |ξ|>τ时，损失值为一常数τ2，这使得损失值不会随误差值的增大而无限增大。

图1 截断最小二乘损失函数图(τ=1.8,Lτ(ξ)=Lsq(ξ)-L2(ξ))Fig.1 Truncated least squares loss function plots(τ=1.8,Lτ(ξ)=Lsq(ξ)-L2(ξ))

与最小二乘损失函数Lsq(ξ)=ξ2相比，最小二乘损失函数的损失值Lsq(ξ) 随误差值ξ的增大而无限增大。当训练样本中存在异常点时，异常点处的误差值ξ通常较大，这导致异常点处具有较大的损失值，因而LSTSVM 的投影超平面较易受异常点的影响。而截断最小二乘损失函数将具有较大误差值的异常点处的损失值设置为某个固定常数，减少了异常点对R-LSTSVM的投影超平面的影响。此外，在3.4节中，将从R-LSTSVM与加权LSTSVM 等价的角度来进一步阐释R-LSTSVM对异常点具有鲁棒性。

2.2 R-LSTSVM的稀疏解

为了求解非凸优化问题式（9）、（10），并得到适合处理大规模数据的算法，本节基于DCA方法、不完全Cholesky分解及表示定理来得到R-LSTSVM的稀疏解。

如果损失函数是凸函数，通过对偶理论，优化模型的最优解w可以表示为：

其中，αi∈ℜ。如果损失函数是非凸函数，则强对偶理论不成立，因此无法通过对偶理论得到式（12）。但是，通过下面的表示定理，可证明式（12）也适用于R-LSTSVM模型。

定理1（表示定理）[20-21]给定非空集合X,ϕ(⋅)为从X到希尔伯特空间的映射，设训练样本集为{(x1,y1),(x2,y2),…,(xm,ym)}∈X×ℜ,g:ℜ+→ℜ 为单调不减实值函数，f:ℜm→ℜ 为任意的损失函数，问题

的最优值w满足式（12）。

由定理1可知，R-LSTSVM的解满足如下定理。

由于Lτ(ξ)为非凸函数，因此模型（13）为非凸优化问题，然而，Lτ(ξ)可表示为两个凸函数相减的形式：

为凸函数。因此，可采用DCA方法[10-11，22]求解模型（15），即通过迭代求解以下凸二次规划问题直至收敛来获得其最优解：

图2 L2(ξ)和(ξ)的图像Fig.2 Plots of L2(ξ) and (ξ)

运用KKT 条件对式（16）进行求解，可得如下线性方程组：

2.3 稀疏R-LSTSVM算法

由3.2 节稀疏解求解过程，可得到如下稀疏RLSTSVM算法。

算法2 稀疏R-LSTSVM算法

SR-LSTSVM 算法中第2 步中ß的确定及P的求解可通过算法1得到。

复杂度分析：第2 步和第3 步的计算复杂度均为O(mr2)，通常r≪m，迭代计算第4 步的计算复杂度为O(tmr)，其中t为迭代次数。因此，该算法总的计算复杂度为O(mr2+tmr)。在非线性情况下LSTSVM 的计算复杂度为O(m3)，因此，在非线性情况下SR-LSTSVM比LSTSVM的计算复杂度低。

由于不完全Cholesky分解只需要O(mr2)的时间复杂度计算核矩阵的至多r列(r≪m)及对角线上元素就可以得到迹范数意义下核矩阵K的最优Nyström 低秩近似，其时间复杂度远低于计算全核矩阵的时间复杂度。并且稀疏R-LSTSVM 算法可得到模型的稀疏解，其时间复杂度O(mr2+tmr)远低于具有稠密解的LSTSVM算法的时间复杂度O(m3)。因此，稀疏R-LSTSVM具有更快的训练速度，更适合处理大规模数据。

2.4 R-LSTSVM的鲁棒性

本节基于文献[23-24]中的思想从加权角度来解释R-LSTSVM具有鲁棒性。

引理Lτ(ξ)=min(τ2,ξ2)可以表示成：

其中

此外：

命题1 R-LSTSVM 模型式（9）中任何稳定点可以通过迭代地求解如下模型得到：

显然，式（35）中的优化问题具有闭式解（31）。式（34）中的优化问题是加入正则项的加权LSTSVM（32）。证毕。

同理可证如下命题2。

命题2 R-LSTSVM 模型（10）中任何稳定点可以通过迭代地求解如下模型得到：

由命题1 和命题2 可知R-LSTSVM 与加入正则项的加权LSTSVM 等价。在模型（32）和（36）中，误差较大的异常点将获得较小的权重，因此模型对异常点具有鲁棒性，从而R-LSTSVM 对异常点也具有鲁棒性。这从加权的角度解释了R-LSTSVM的鲁棒性。

3 实验

3.1 实验设计

通过在模拟数据集和真实数据集上的实验来验证SR-LSTSVM 对异常点的鲁棒性、解的稀疏性和处理大规模数据的能力。

为验证算法的性能，将SR-LSTSVM算法与以下算法进行比较：

（1）LSTSVM：最小二乘孪生支持向量机[3]，损失函数为最小二乘损失，LSTSVM通过求解两组线性方程组来确定两个非平行的投影超平面。

（2）LSTBSVM：基于最小二乘的孪生有界支持向量机（least squares twin bounded support vector machines，LSTBSVM）[26]，该模型在LSTSVM中加入了正则项。

（3）W-LSTSVM：加权最小二乘孪生支持向量机[4]，通过对样本损失增加不同权重，来提高算法鲁棒性。

（4）WWL-STSVM：广泛权重的最小二乘孪生支持向量机[5]，对于每个模型，在正负两类样本上都增加权重。

（5）PCP-LSSVM：基于选主元Cholesky分解的原空间LSSVM[19]，该算法为一种稀疏最小二乘支持向量机算法。

（6）SR-LSSVM：一种稀疏鲁棒最小二乘支持向量机算法（Sparse R-LSSVM，SR-LSSVM）[27]。

在模拟数据集和中小规模真实数据集上将新算法与LSTSVM、LSTBSVM、W-LSTSVM 和WWL-STSVM结果进行对比。在大规模真实数据集上，由于上述算法占用内存较大，消耗时间较长，因此将新算法与两种稀疏算法PCP-LSSVM和SR-LSSVM的结果进行对比。

参数选取方法为首先采用网格搜索方式确定最优参数所在区间，然后细化该搜索区间，得到最优参数取值。核函数采用Gaussian核函数，即K(xi,xj)=exp(-‖xi-xj‖2/(2σ2))，其中σ为参数，取值范围为[10-10,1010]。在WLSTSVM、WWL-STSVM 和LSTBSVM 中，C1和C2为惩罚因子，C3和C4为正则化参数。WWL-STSVM 中的R为权重参数，取值范围为[0,10]。SR-LSSVM 和PCP-LSSVM 中的C为正则化参数。在SR-LSTSVM中，停止参数ρ=10-4，固定光滑参数p=105。C、C1、C2、C3、C4的取值范围为[10-10,1010]。τ的取值范围为[0,102]。

效果性能评估指标：采用分类准确率评估模型分类性能：

所有实验均在Intel i5（2.50 GHz）处理器和内存为4.0 GB的平台上实现，编程环境为Matlab R2014a。

3.2 模拟数据集实验

模拟数据点由位于两条相交直线上的点扰动产生，正类和负类数据均为200个。在数据集中随机选取3/4样本点作为训练样本，剩余样本点作为测试样本，在训练样本中随机选取五个样本点并改变其标签来模拟异常点。为了验证SR-LSTSVM的鲁棒性，在无异常点和有异常点的模拟数据集上进行对比实验。

图3 所给出了五种对比算法在无异常点和取相同异常点时的投影超平面。在图3 中正类的异常点用红色菱形表示，负类异常点用蓝色五角星表示，正类样本点的投影超平面用红色实线表示，负类样本点的投影超平面用黑色实线表示。通过图3可以看出：加异常点前后，SR-LSTSVM的投影超平面变化比其他四种算法小，说明SR-LSTSVM 比其他四种算法具有更好的鲁棒性。这是由于SR-LSTSVM 的损失函数是截断最小二乘损失函数，当训练样本中存在异常点时，截断最小二乘损失函数会将具有较大误差值的异常点处的损失值设置为一个常数，从而减少异常点对投影超平面的影响。W-LSTSVM 对于每一个模型，仅对其中的一类数据加权重，对于含有交叉噪声的数据集投影超平面变化较大。WWL-STSVM 对于每个模型，在正负两类样本上都增加权重，因此加异常点前后投影超平面的变化比W-LSTSVM 小，但仍比SR-LSTSVM 大。稀疏性方面，SR-LSTSVM采用不完全Cholesky分解选出的样本作为支持向量，如图3（i）、（j）所示。其中，正类支持向量（SV）用粉色实心圆表示，负类SV用绿色菱形表示。然而，其他算法的解不具有稀疏性，几乎所有样本都是SV。只在SR-LSTSVM 上标记SV。图3（i）、（j）表明SR-LSTSVM在有异常点和无异常点的模拟数据集上都只需要两个SV，表明SR-LSTSVM算法具有稀疏性。

图3 模拟数据集上加异常点前后投影超平面对比Fig.3 Comparison of projection hyperplane on simulated datasets before and after adding outliers

为了进一步体现SR-LSTSVM 在模拟数据集上的分类性能，表1给出了五种算法在模拟数据集上有异常点和无异常点情况下的参数设置、准确率和方差，其中准确率和方差是算法独立运行100 次取得的平均值。表1 表明在无异常点和有异常点的模拟数据集上SRLSTSVM 比其他算法具有更高的准确率。在数据集加入异常点后LSTSVM、LSTBSVM 和W-LSTSVM 三种算法的准确率明显下降，而WWL-STSVM和SR-LSTSVM的准确率下降较小，但是WWL-STSVM 的下降幅度仍比SR-LSTSVM大，因此，SR-LSTSVM比其他四种算法具有更好的鲁棒性。

表1 模拟数据集上算法的参数设置和分类准确率Table 1 Parameter setting and classification accuracy of algorithms on simulation data sets

3.3 中小规模真实数据集实验

在五组中小规模真实数据集上进行实验，数据集均来自LIBSVM网站（https：//www.csie.ntu.edu.tw/～cjlin/libsvmtools/datasets/），其中Shuttle 包含七个类别，选取第四类和第五类数据。Segment 包含七个类别，选取第二类和第三类数据。Satimage包含六个类别，选取第二类和第三类数据。Pendigits包含九个类别，选取第三类和第四类数据。在每组数据集中随机选取3/4样本点作为训练样本，剩余样本点作为测试样本，在训练样本中随机选取10%的样本点并改变其标签来模拟异常点。为验证SR-LSTSVM的鲁棒性，所有实验均在含异常点的数据集上进行。

表2和表3分别给出了五种算法在中小规模数据集上实验的参数设置和实验结果，其中nSVs 表示支持向量的个数。所有实验结果均为算法独立运行100次取得的平均值。从表3中可以看出SR-LSTSVM在Segment、Satimage、SVMguide1 和Pendigits 这四组数据上的分类效果均好于其他算法，在Shuttle 上的准确率比WWLSTSVM 略差，但SR-LSTSVM 的训练速度比WWLSTSVM 快。图4 给出了五种算法在五组数据集上准确率排名的平均值。从图4可以看出SR-LSTSVM是五种算法中分类准确率最高的模型，这是由于SR-LSTSVM采用的是截断最小二乘损失函数，当训练数据中存在异常点时，截断最小二乘损失函数会将具有较大误差值的异常点的损失值设置为一个常数，从而减少异常点对投影超平面的影响，得到更符合数据分布的投影超平面。这提高了SR-LSTSVM 的分类准确率。训练速度方面，SR-LSTSVM 采用了核矩阵的低秩近似矩阵，避免了计算全核矩阵，具有较低的计算复杂度。因此，SR-LSTSVM比其他四种算法具有更快的训练速度。稀疏性方面，SR-LSTSVM 的支持向量的个数比其他算法少，这是由于SR-LSTSVM采用不完全Cholesky分解选择支持向量，得到了具有稀疏性的解，而其他算法得到的解中几乎所有样本均是支持向量，不具有稀疏性。因此，SR-LSTSVM比其他四种算法具有更少的支持向量。

表3 中小规模数据集上算法的实验结果Table 3 Experimental results of algorithms on small and medium-sized benchmark datasets

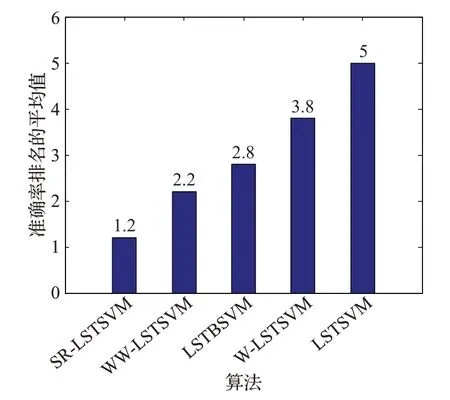
图4 五种算法分类准确率排名的平均值对比Fig.4 Comparison of average value of classification accuracy ranking of five algorithms

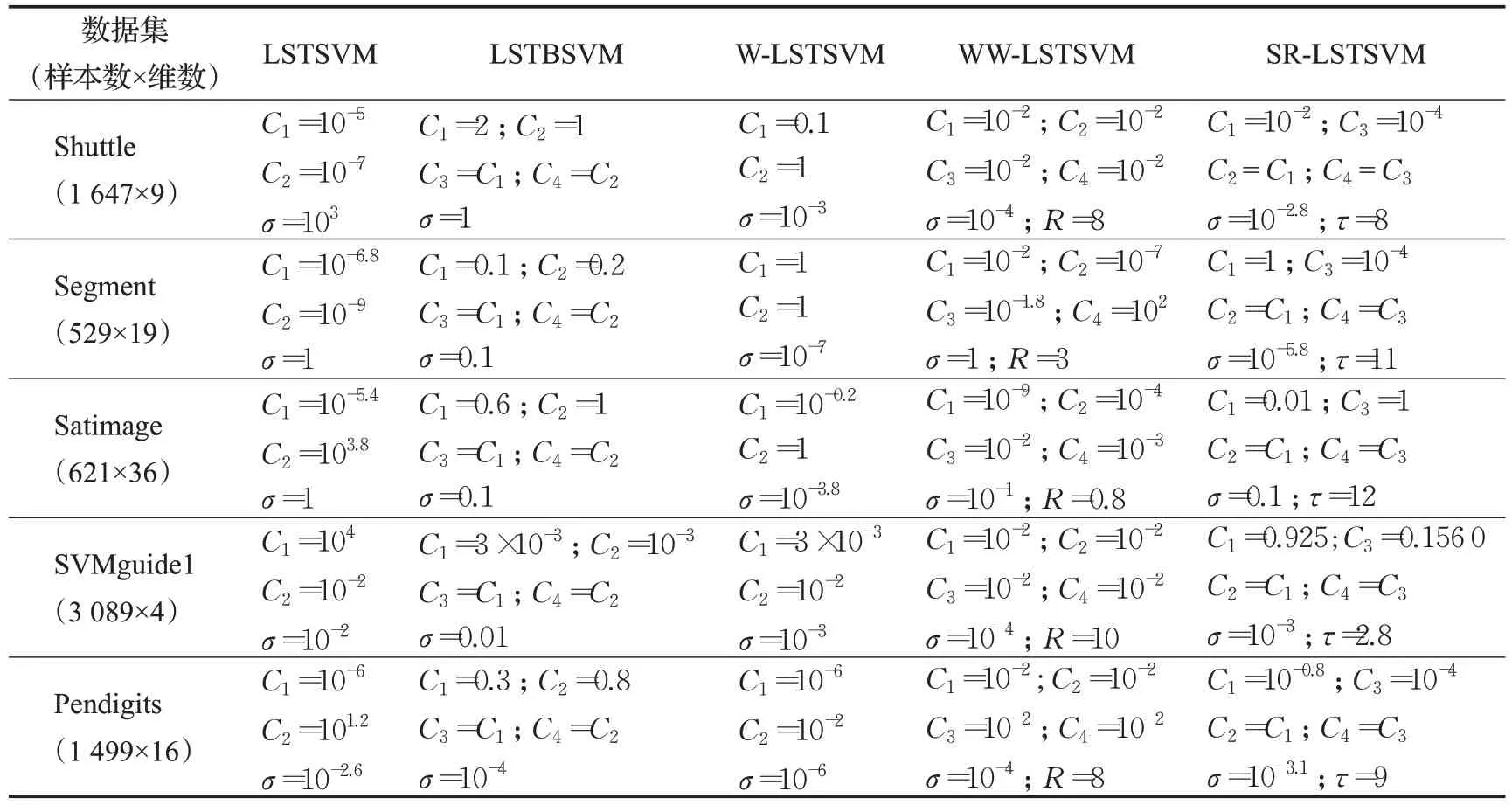
表2 中小规模数据集上算法的参数设置Table 2 Parameter settings for algorithms on small and medium-sized benchmark datasets

3.4 大规模真实数据集实验

为了验证SR-LSTSVM处理大规模数据的能力，将SR-LSTSVM与两种稀疏算法SR-LSSVM和PCP-LSSVM在大规模真实数据集上的实验结果进行比较。数据集均来自LIBSVM 网站，其中SensIT_Vehicle 包含三个类别，选取第二类和第三类数据实验。在每组数据集中随机选取3/4 样本点作为训练样本，剩余样本点作为测试样本，在训练样本中随机选取10%的样本点并改变其标签来模拟异常点。为验证SR-LSTSVM的鲁棒性，所有实验均在含异常点的数据集上进行。

表4和表5分别给出了在大规模数据上三种稀疏算法的参数设置和实验结果，所有结果均为算法独立运行10 次取得的平均值。从表5 中可以看出：准确率方面，SR-LSSVM 和SR-LSTSVM 比PCP-LSSVM 准确率更高，这是由于SR-LSTSVM和SR-LSSVM均采用了对异常点具有鲁棒性的损失函数，而PCP-LSSVM采用的是易受异常点影响的最小二乘损失函数。SR-LSTSVM在W8a 和IJCNN 这两组数据上的分类效果比SR-LSSVM好。训练时间方面，SR-LSTSVM 的训练时间均少于SR-LSSVM。这是由于SR-LSTSVM通过计算两个规模更小的线性规划问题得到最优解，与SR-LSSVM相比具有更低的计算复杂度，因而具有更快的训练速度。稀疏性方面，SR-LSTSVM、SR-LSSVM 和PCP-LSSVM 三个算法均具有稀疏性，这是由于这三种算法均采用不完全Cholesky分解选出的样本作为支持向量机。综上所述，SR-LSTSVM 具有较高的分类准确率和较快的训练速度，更适合处理含异常点的大规模数据分类问题。

表4 大规模数据集上稀疏算法的参数设置Table 4 Parameter settings for sparse algorithms on large-scale data sets

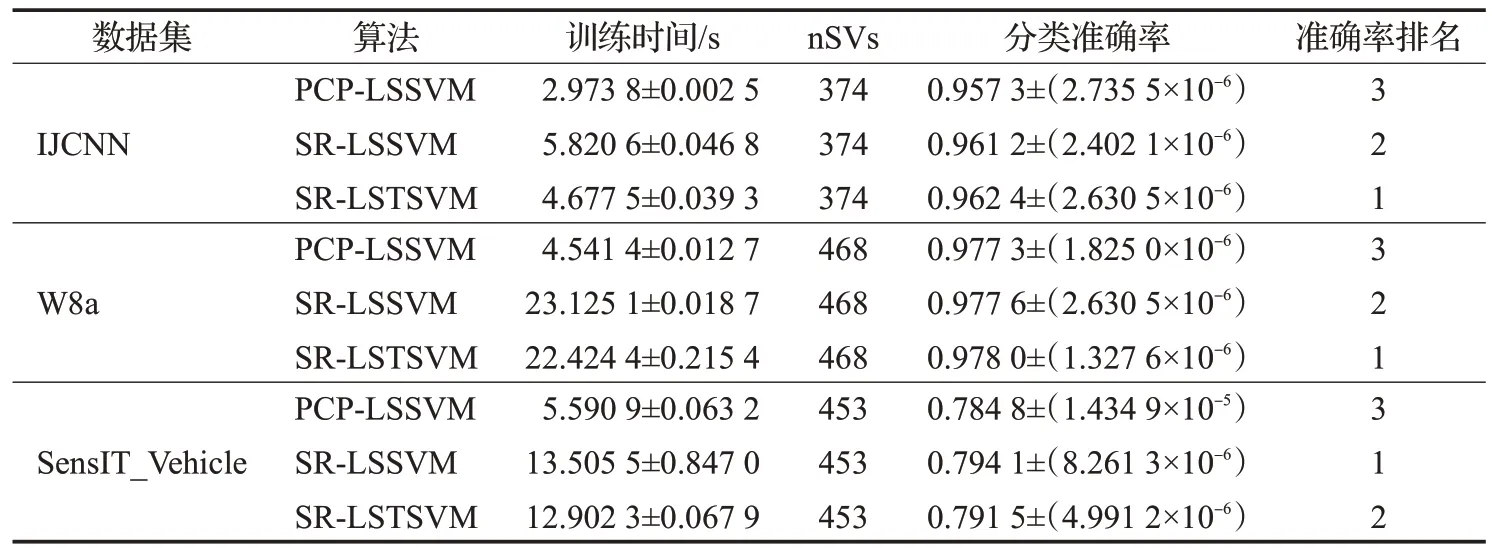
表5 大规模数据集上稀疏算法的实验结果Table 5 Experimental results of sparse algorithms on large-scale data sets

4 总结

LSTSVM 模型易受异常点的影响且其解缺乏稀疏性。为克服这些缺陷，基于截断最小二乘损失提出了具有鲁棒性的LSTSVM（R-LSTSVM），并得到了R-LSTSVM的稀疏解，提出了稀疏R-LSTSVM（SR-LSTSVM）算法。此外，从加权的角度解释了R-LSTSVM 具有鲁棒性。实验结果表明，SR-LSTSVM 比其他算法具有更好的分类准确率和更快的训练速度，是处理含异常点的大规模分类问题的合适选择。