基于互信息的多级特征选择算法

雍菊亚，周忠眉*

（1.闽南师范大学计算机学院，福建漳州 363000；2.数据科学与智能应用福建省高等学校重点实验室，福建漳州 363000）

（∗通信作者电子邮箱64523040@qq.com）

0 引言

随着大数据的不断增长［1］，特征选择在机器学习中受到越来越多的关注。它的目的是从原始特征空间中选取一组具有代表性的特征子集，用来提升分类器的训练速度，从而达到比较好的训练效果［2］。因此，特征选择成为了大数据背景下的一个重要研究方向。它通常的做法是使用某种评价准则从原始特征空间中选择特征子集。迄今为止，学者们从多个角度对特征选择进行了定义，如特征子集是否能识别目标、预测精度是否降低、原始数据类分布是否会改变等。但是，如何挑选出一个符合上述条件且尽可能小的特征子集成为了一个研究难点。

目前，大多数特征算法［3-8］都可以选出强相关特征、去除无关特征，并且在一定程度上去除了冗余特征。比如：文献［9］提出的ReliefF 算法通过特征对近距离样本的区分能力赋予特征权重，并选取满足权重阈值的特征。文献［10］提出的条件互信息最大化准则（Conditional Mutual Information Maximization criterion，CMIM）算法在挑选与标签相关的特征的同时，也利用条件互信息对冗余部分进行了最大化处理。文献［11］提出的基于联合互信息（Join Mutual Information，JMI）的特征选择方法在冗余部分进行了均值化处理，基于联合互信息选取累加和值大的特征，并认为这些特征构成了最优特征子集。文献［12］提出的mRMR（minimal-Redundancy-Maximal-Relevance criterion）算法和文献［13］提出的改进的最大相关最小冗余（improve Maximum Relevance and Minimum Redundancy）特征搜索算法通过特征与标签的相关度以及与已选特征子集的冗余度对特征进行打分，并选取得分高的特征。文献［14］提出的双输入对称关联（Double Input Symmetrical Relevance，DISR）算法挑选出所有表现最优的特征，认为其形成的特征子集有较高的分类性能。文献［15］提出的FCBF（Fast Correlation-Based Filter solution）算法通过特征与标签的相关度选取满足相关度阈值的特征，然后再利用马尔可夫毯原理进行去冗余。上述几种特征选择算法出发点不同，各有侧重点，也都取得了较好的分类性能。

但是，理想的特征选择算法要能去除无关和弱相关且冗余的特征，并能保留强相关［16］和弱相关非冗余特征。因此，在挑选出强相关特征、去除无关特征的前提下，冗余特征的处理决定了特征子集分类性能的好坏。首先，若是相关度的临界值设置过高，算法挑选出的强相关特征就会过少，容易遗漏重要特征；若是过低，所选取的特征数量过大，需要复杂的去冗余过程。此外，某些特征与标签的相关度不高，但与其他特征组合后，会增加它们与标签的相关度，这样的特征更不易被选进。文献［17］提出的最大相关最小冗余联合互信息（Joint Mutual information of Max-relevance and min-redundanCy，JMMC）算法通过条件互信息和交互信息，并利用最大相关最小冗余的思想，有效地识别出相关、冗余和无关特征，但是也会遗漏与标签相关度不高，但与其他标签组合后有较强相关度的特征。基于上述情况，本文提出了一种基于互信息的多级特征选择算法（Multi-Level Feature Selection algorithm based on Mutual Information，MI_MLFS）。该算法的目的就是要克服当前过度去冗余而导致有用信息丢失的局限性。根据特征与标签的相关度，该算法将特征分成三类：强相关、次强相关和其他特征，并分别对这三类特征采用不同的方式进行选取：1）MI_MLFS 直接选进强相关特征；2）对于次强相关特征，MI_MLFS 利用互信息衡量特征与标签的相关度，以及特征与标签、已选特征子集的相关度，两者差值较大的特征就被认为是冗余度较低的特征，将其加入到已选特征子集中；3）对于其他特征，MI_MLFS 度量它们与已选特征子集里的特征进行组合后与标签的相关度，并将相关度有所提升的特征加入到已选特征子集中。实验结果表明，MI_MLFS 具有较优的分类性能。

1 相关定义

假设数据集为T，且T={t1，t2，…，tn}，其中n表示此数据集的样本数量。设此数据集的特征集合为F，且F={f1，f2，…，fm}，其中m表示特征个数。设此数据集的标签集合为C，且C={c1，c2，…，cs}，其中s表示此数据集的标签值的个数。

定义1信息熵［18］。设fi为F中的任意特征，且fi={fi1，fi2，…，fil}，其中l表示特征fi的特征值的个数。则fi的信息熵定义为：

其中，p(fij)表示值fij在数据集中发生的概率。

定义2联合熵［19］。设fi为F中的任意特征，且fi={fi1，fi2，…，fil}，标签集合C={c1，c2，…，cs}，则特征fi和标签集合C的联合熵定义为：

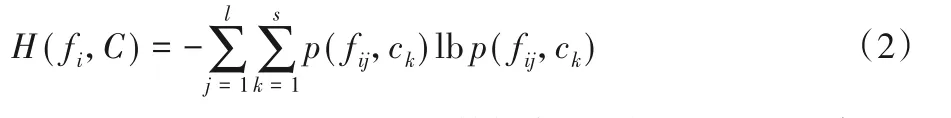
其中，p(fij，ck)表示fij和ck在整个数据集中同时发生的概率。

定义3互信息［20］。设fi为F中的任意特征，且fi={fi1，fi2，…，fil}，标签集合C={c1，c2，…，cs}，则特征fi和标签集合C的互信息定义为：

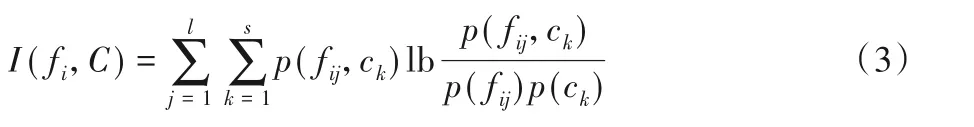
定义4联合属性的互信息。设fi、fj为特征集合F中的任意两个特征，且fi={fi1，fi2，…，fil}，fj={fj1，fj2，…，fjh}，其中，l表示特征fi的特征值的个数，h表示特征fj的特征值的个数。则fi和fj的联合属性与标签集合C的互信息定义为：

定义5特征与标签的相关度［12］。设fi为特征集合F的任意一个特征，则fi与标签C的相关度定义为：

定义6特征之间的冗余度［21］。设一特征集合为A，且A={f1，f2，…，fk}，其中，k为A中的特征个数。fi为A中的任意一个特征，则fi与集合A中其他特征的冗余度定义为：

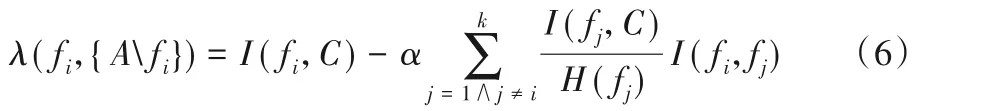
其中，参数α∈(0，1)。λ(fi，{Afi})的值越小，说明fi在集合A中冗余度越大。

定义7组合特征的相关度。设fi、fj为任意两个特征，则特征fi与fj的组合特征的相关度定义为：

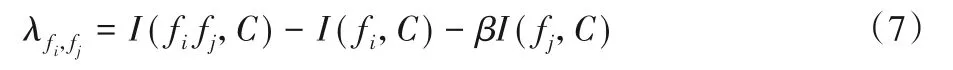
其中，β∈(0，1)。λfi，fj的值越大，就表示fi与fj的联合属性的互信息越大，也表示特征fi与fj的组合特征与标签的相关度越大。同时，组合特征的相关度反映了联合属性的互信息与各特征互信息之间的关系。

定义8强相关特征。设δ1为给定的一个相关度阈值，fi为特征集合F中的任意一个特征，若特征fi与标签集合C的相关度大于δ1，则称fi为特征集合F的强相关特征。

定义9次强相关特征。设δ1、δ2为给定的两个相关度阈值，且δ1>δ2，fi为特征集合F中的任意一个特征。若特征fi与标签集合C的相关度大于δ2且小于δ1，则称fi为特征集合F的次强相关特征。

定义10基于组合的强相关特征。设特征集合A={f1，f2，…，fk}，其中，k为集合A中的特征个数，∀fi∉A。计算fi与特征集合A中所有特征组合的λfi，fj值，得到λ={λfi，f1，λfi，f2，…，λfi，fk}。如果集合λ中存在90%的λfi，fj> 0，则称fi为关于A的基于组合的强相关特征。

2 算法描述

为了不漏选重要的特征，同时尽量少选冗余特征，MI_MLFS 根据每个特征与标签的相关度，将特征集合F划分为三个部分，即强相关特征集、次强相关特征集和其他特征集，并对这三个集合的特征分别用不同的方法进行选取。首先，MI_MLFS 选取所有强相关特征；其次，对于次强相关特征集，根据定义6 中特征之间的冗余度公式，去除其冗余的特征；最后，对于其他特征的集合，根据定义7 中特征组合后相关度的计算公式，选取能增强集合相关度的特征。下面给出MI_MLFS整个选取过程的具体步骤和伪代码。

2.1 三类特征的划分

MI_MLFS 将特征集合F划分为强相关特征集、次强相关特征集和其他特征集。具体划分过程如下：

1）对于特征集合F={f1，f2，…，fm}，根据式（5），计算F中每个特征与标签的相关度，得到所有特征相关度的集合，记为R，且令R={R1，R2，…，Rm}。其中，Ri代表第i个特征与标签的相关度。

2）给定相关度阈值δ1、δ2，且δ1∈(0，1)，δ2∈(0，1)，δ1>δ2。对于特征相关度的集合R，若Ri>δ1，则根据定义8，特征fi为强相关特征，从而得到所有强相关特征的集合，并记为S1；若δ1>Ri>δ2，则根据定义9，特征fi为次强相关特征，从而得到次强相关特征的集合，并记为S2。最后，F-S1-S2为其他特征的集合，并记为S3。

2.2 集合S1和集合S2中特征的选取

由于集合S1中是强相关特征，算法直接选取S1中所有特征。对于次强相关特征集合S2，算法去除S2中的冗余特征，具体方法如下：

1）给定阈值t，t∈(0，1)。在次强相关集合S2中选取特征与标签的相关度大于t的所有特征，得到S2的特征子集M，即M为次强相关特征集合中相关度较大的特征，记=S2-M。

2）选取集合中相关度最大的特征fi，将其添加到子集M中。根据定义6，计算M中每个特征与其他特征的冗余度，并删除集合M中冗余度最大的特征，将删除后的集合记为Mi。

3）选取集合(-fi)中相关度最大的特征fj，将其添加到子集Mi中。根据定义6，计算Mi中每个特征与其他特征的冗余度，并删除集合Mi中冗余度最大的特征，将删除后的集合记为Mj。

4）选取集合(-fi-fj)中相关度最大的特征fk，将其添加到子集Mj中。根据定义6，计算Mj中每个特征与其他特征的冗余度，并删除集合Mj中冗余度最大的特征，将删除后的集合记为Mk。

5）以此类推，直至集合(-fi-fj-…-fh)中没有特征，并得到集合Mh，且集合Mh中的特征均为次强相关且低冗余的特征。

2.3 其他特征的集合S3中特征的选取

对于集合S3中的所有特征，利用2.2 节得到的集合Mh，根据定义10 中的相关度定义，确定是否将S3的特征选入Mh中。具体实施如下：

1）选取集合S3中相关度最大的特征fi，根据定义7，计算特征fi与集合Mh中的每个特征组合后与标签的相关度，得到相关度集合λ1。如果集合λ1中存在90%的λfi，fj> 0，那么fi为关于Mh的基于组合的强相关特征，将其加入到集合Mh中。

2）选取集合S3中相关度最大的特征fs，根据定义7，计算特征fs与集合Mh中的每个特征组合后与标签的相关度，得到相关度集合λ2。如果集合λ2中存在90%的λfs，fj> 0，那么fs为关于Mh的基于组合的强相关特征，将其加入到集合Mh中。

3）选取集合(S3-fi-fs)中相关度最大的特征fk，根据定义7，计算特征fk与集合Mh中的每个特征组合后与标签的相关度，得到相关度集合λ3。如果集合λ3中存在90%的λfk，fj>0，那么fk为关于Mh的基于组合的强相关特征，将其加入到集合Mh中。

4）以此类推，直至集合(S3-fi-fs-…-fh)为空集。最后，集合S3中所有特征均被确定是否选取。

2.4 MI_MLFS的伪代码

根据MI_MLFS 的三级选取过程，给出下面相应的三个算法。其中，算法1 为特征集合的划分及强相关特征的选取，算法2为次强相关集合中冗余特征的去除，算法3为基于组合的强相关特征的选取。

算法1 主要是根据相关度阈值将原始特征空间分成强相关、次强相关和其他特征集。选取强相关特征后，根据算法2和算法3 分别对次强相关特征和其他特征进一步挑选。其中，第2）～4）行为特征与标签相关度的计算，第6）行为强相关特征的选取，第9）行为次强相关特征的选取，第13）行为其他特征的选取。

算法2 主要是从次强相关特征中选取冗余度较低的特征。第5）～7）行为关键步骤，计算集合M中的每个特征与其他特征的冗余度。第8）～9）行将冗余度最大的特征从已选特征子集中删除。

算法3 主要是在其他特征集合中挑选出基于组合的强相关特征。第3）行是关键步骤，考虑待选特征与已选特征进行组合后，是否能增强已选特征与标签的相关度。第8）～10）行表示若90%的已选特征与其组合后，与标签的相关度有所增强，则认为此特征为基于组合的强相关特征。

3 实验与结果分析

3.1 实验设计与数据集

为了验证MI_MLFS的有效性，选用ReliefF算法［9］、mRMR算法［13］、JMI算法［11］、CMIM 算法［10］和DISR 算法［14］进行对比实验。数据集的简要描述如表1 所示。实验平台为PC（Windows 10，Intel Core i7-8550U CPU@ 1.80 GHz 1.99 GHz），使用的软件为Matlab 2016a 和R。本文所使用的分类器是支持向量机（Support Vector Machine，SVM）和分类回归树（Classification and Regression Tree，CART）。

3.2 结果分析

本文均采用分类准确率来预测特征算法的优劣。同时，为了进一步说明不同算法在不同分类器和数据集上的优劣，本文使用Win/Draw/Loss 来统计并分析算法两两之间的差异。Win 表示算法A 优于B，Draw 表示算法A 等于B，Loss 表示算法A差于B［17］。

表2的数据表示6种算法在不同数据集上，采用10折交叉验证法［22］在SVM 分类器得到的平均分类准确率结果。从表2可以看出，MI_MLFS 在15 个数据集上的分类准确率均比ReliefF算法高，并且MI_MLFS在这15个数据集上的平均准确率（AVG）相较ReliefF 算法提高了6.25 个百分点。MI_MLFS在15个数据集中的14个上的分类准确率均比mRMR算法高，并且MI_MLFS 在这15 个数据集上的平均准确率相较mRMR算法提高了4.89 个百分点。MI_MLFS 在15 个数据集中的14个上的分类准确率均比JMI 算法高，并且MI_MLFS 在这15 个数据集上的平均准确率比JMI 算法提高了6.81 个百分点。MI_MLFS 在15 个数据集上的分类准确率均比CMIM 算法高，并且MI_MLFS在这15个数据集上的平均准确率比CMIM算法提高了6.18 个百分点。MI_MLFS 在15 个数据集上的分类准确率均比DISR 算法高，并且MI_MLFS 算法在这15 个数据集上的平均准确率相较DISR算法提高了7.31个百分点。

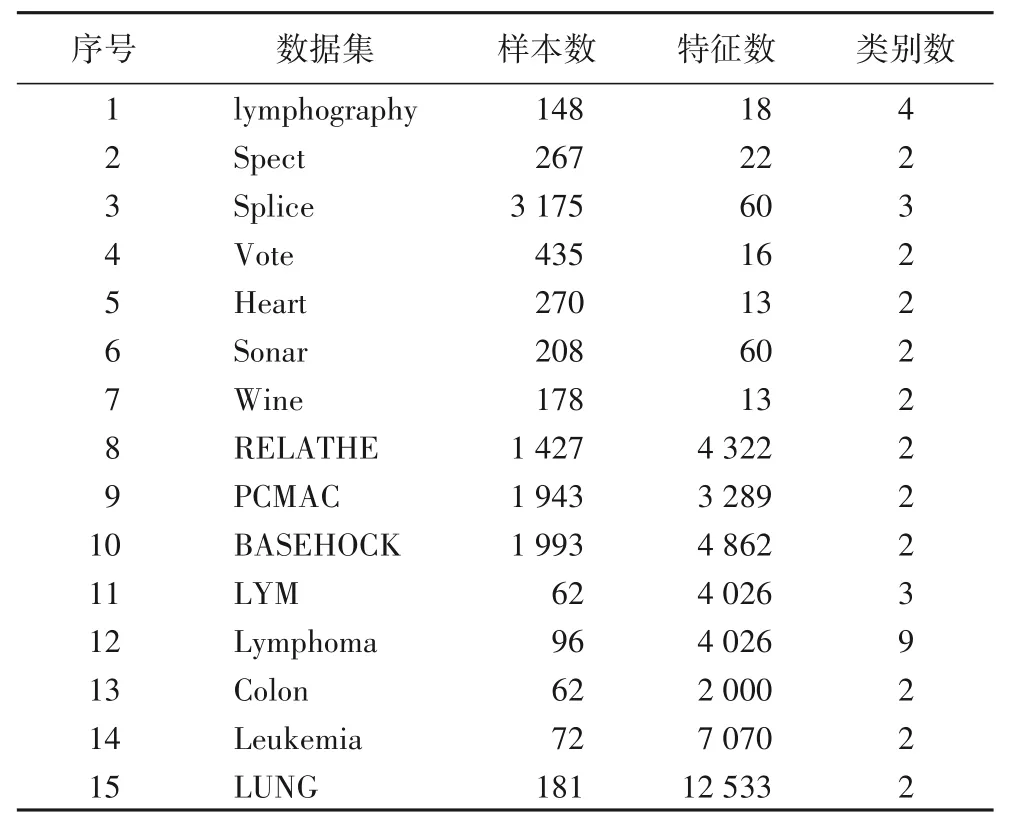
表1 实验数据集Tab.1 Datasets used in experiments

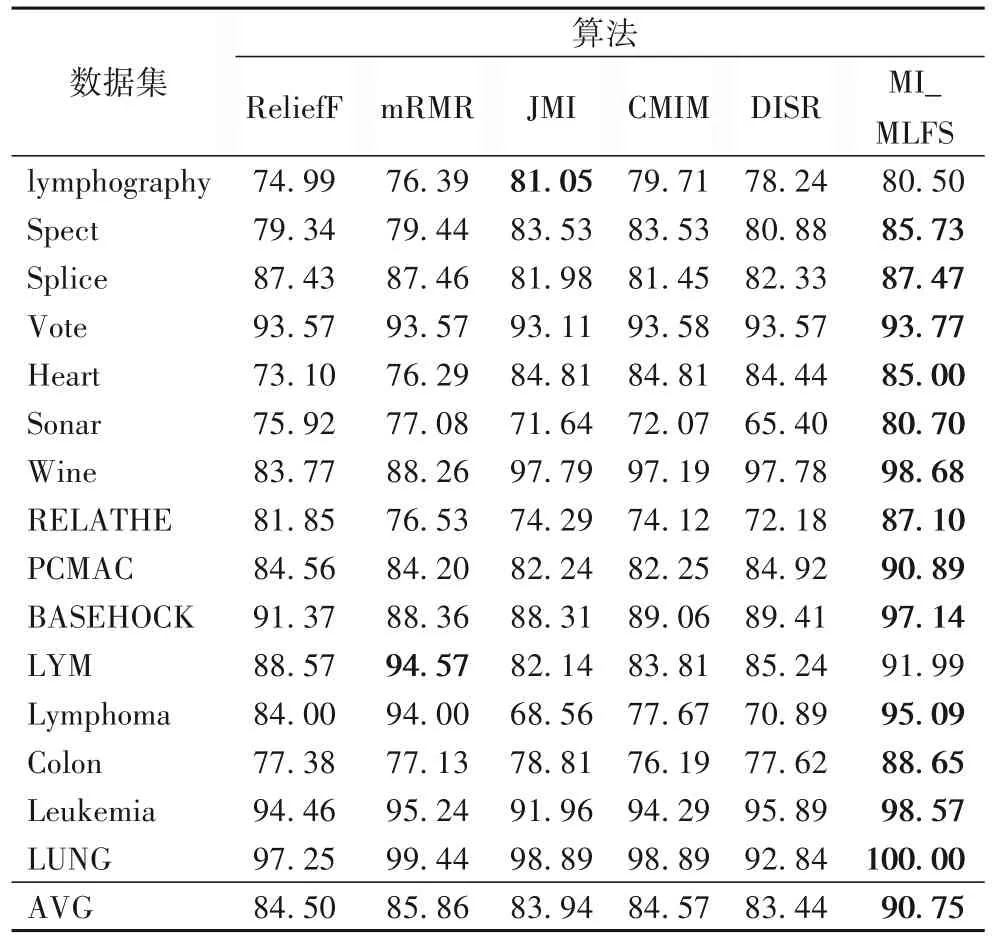
表2 基于SVM分类器的不同算法在不同数据集上的分类准确率 单位：%Tab.2 Classification accuracy of different algorithms on different datasets based on SVM classifier unit：%

表3 表示6 种算法在不同数据集上，采用10 折交叉验证法在CART 分类器得到的平均分类准确率结果。从表3 可以看出，MI_MLFS 在15 个数据集中的14 个上的分类准确率均比ReliefF 算法高，并且MI_MLFS 在这15 个数据集上的平均准确率相较ReliefF 算法提高了4.88 个百分点。MI_MLFS 在15个数据集中的14个上的分类准确率均比mRMR算法高，并且MI_MLFS 在这15 个数据集上的平均准确率相较mRMR 算法提高了3.93个百分点。MI_MLFS 在15个数据集中的13个上的分类准确率均比JMI 算法高，并且MI_MLFS 在这15 个数据集上的平均准确率相较JMI 算法提高了5.08 个百分点。MI_MLFS 在15 个数据集中的14 个上的分类准确率均比CMIM 算法高，并且MI_MLFS 在这15 个数据集上的平均准确率相较CMIM 算法提高了4.72 个百分点。MI_MLFS 在15 个数据集中的13 个上的分类准确率均比DISR 算法高，并且MI_MLFS 在这15 个数据集上的平均准确率比DISR 算法提高了4.21个百分点。

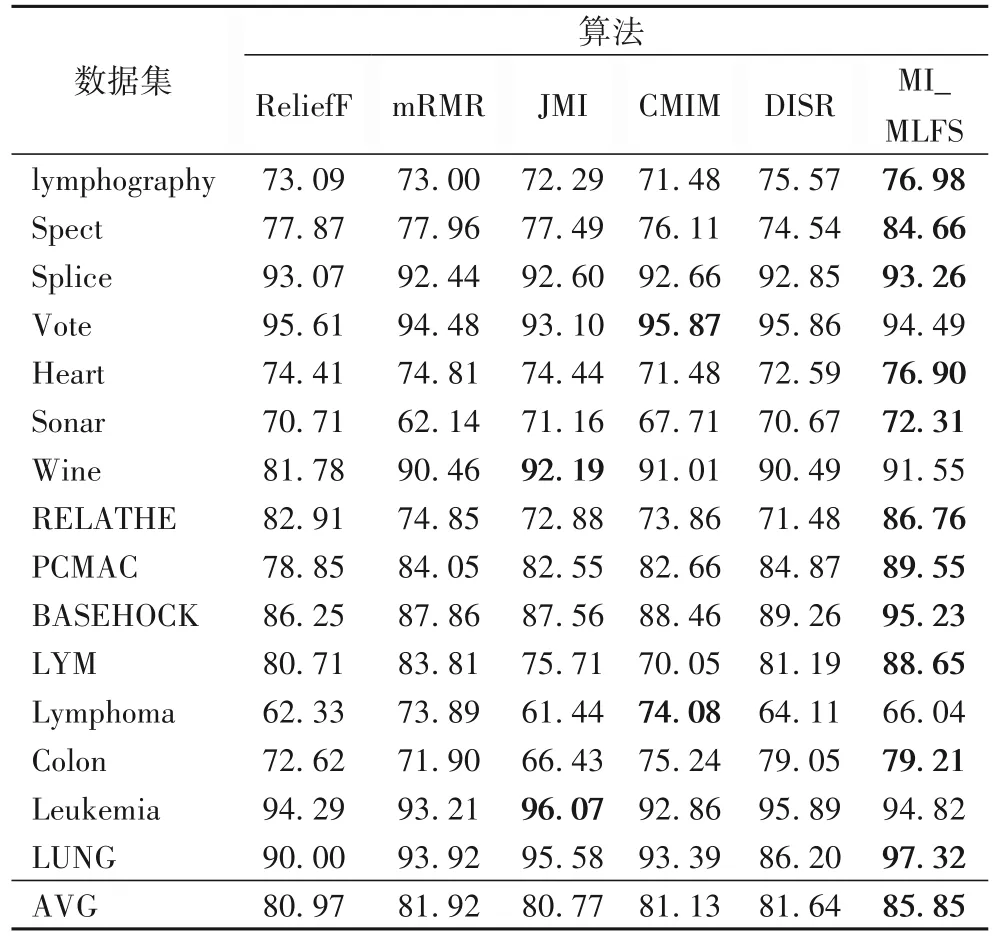
表3 基于CART分类器的不同算法在不同数据集上的分类准确率单位：%Tab.3 Classification accuracy of different algorithms on different datasets based on CART classifier unit：%

表4 是MI_MLFS 与其他5 种算法在SVM 分类器和CART分类器上的平均分类准确率两两比较的结果。例如，表4 中第三行第二列的15/0/0 表示MI_MLFS 与ReliefF 算法在SVM分类器上的对比结果：在15个数据集上MI_MLFS的性能比较好，在0 个数据集上与ReliefF 算法性能相同，在0 个数据集上MI_MLFS 的性能较差。由表4 可以看出，在使用SVM 分类器时，MI_MLFS在所有数据集上均优于ReliefF 算法、CMIM 算法和DISR 算法。与mRMR 算法以及JMI 算法相比，均只在一个数据集上，MI_MLFS 略逊一点。在使用CART 分类器时，MI_MLFS 在所有数据集上均优于ReliefF 算法和mRMR 算法。和JMI 算法以及DISR 算法相比，均只在一个数据集上，MI_MLFS 略逊一点。和CMIM 算法相比，在13 个数据集上，MI_MLFS的分类准确率较高。

表4 MI_MLFS算法与其他基于特征选择算法的Win/Draw/Loss分析Tab.4 Win/Draw/Loss analysis of MI_MLFS and other feature selection algorithms

3.3 大样本高维数据集的分析

图1 表示当使用SVM 分类器时，在RELATHE、PCMAC 和BASEHOC 这3 个数据集上，6 种算法在所选特征数相同的情况下，采用10 折交叉验证法得到的各算法的平均分类准确率。其中，横坐标表示依次递増的所选特征子集比例，纵坐标表示平均分类精度。根据图1 的结果可知，在同等特征数的情况下，MI_MLFS 都具有明显优势。这是因为MI_MLFS 的三级选取过程不仅选取了与标签强相关的单个特征，还选取了基于组合的强相关特征。在特征比例为0.1%～0.3%的情况下，MI_MLFS 的分类性能尤为显著。由此可以看出，面对大样本高维数据集，MI_MLFS 可以选取一个规模较小的，并且分类性能较好的特征子集。

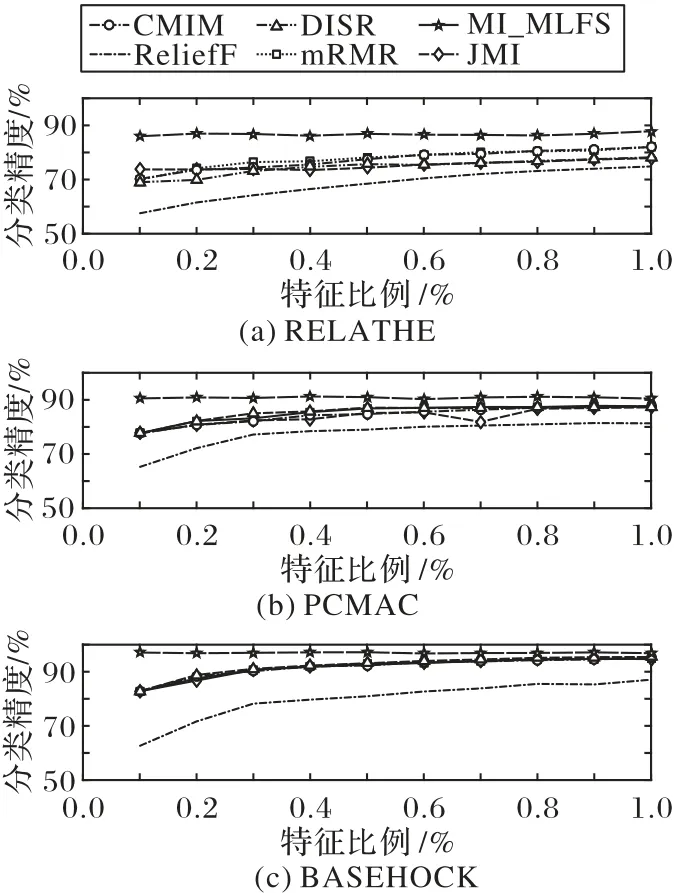
图1 基于SVM分类器在大样本高维数据集上的分类准确率和所选特征比例Fig.1 Classification accuracy and proportion of selected feature subset on datasets with large and high-dimensional samples based on SVM classifier

图2 表示当使用CART 分类器时，在RELATHE、PCMAC和BASEHOC 这3 个数据集上，6 种算法在所选特征数相同的情况下，采用10 折交叉验证法得到的各算法的平均分类准确率。其中，横坐标表示依次递増的所选特征子集比例，纵坐标表示平均分类精度。

根据图2 的结果可知，在同等特征数的情况下，MI_MLFS在这3 个大样本高维数据集上，相较其他5 种算法，具有较高的分类准确率。其中，在特征比例较小的情况下，MI_MLFS的分类性能较为显著。由此表明，与其他5 种算法相比，MI_MLFS 在大样本高维数据集上可以选取出规模更小、分类精度更好的特征子集。

3.4 小样本高维数据集的分析

图3 表示当使用SVM 分类器时，在LYM、Lymphoma、Colon、Leukemia 和LUNG 这4 个小样本高维数据集上，6 种算法在所选特征数相同的情况下，得到的各算法分类准确率的结果。其中，横坐标表示依次递増的所选特征子集比例，纵坐标表示平均分类精度。

根据图3 的结果可知，MI_MLFS 在LYM、Lymphoma、Leukemia 和LUNG 这4 个小样本高维数据集上的分类精度均优于其他5 种算法。在Colon 数据集上，当特征比例为0.3%时，MI_MLFS具有最好的分类性能。

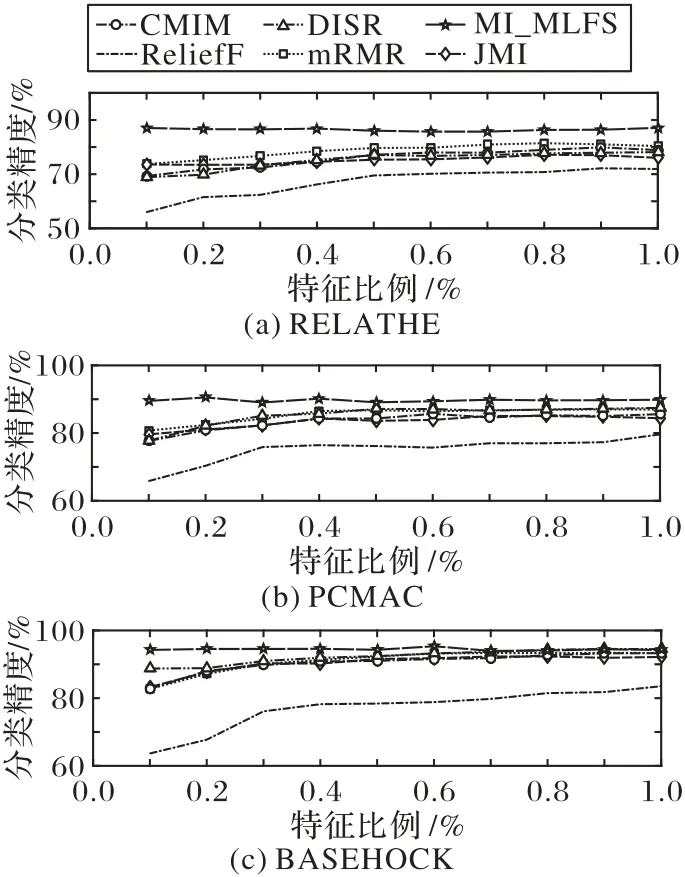
图2 基于CART分类器的大样本高维数据集上的分类准确率和所选特征比例Fig.2 Classification accuracy and proportion of selected feature subset on datasets with large and high-dimensional samples based on CART classifier

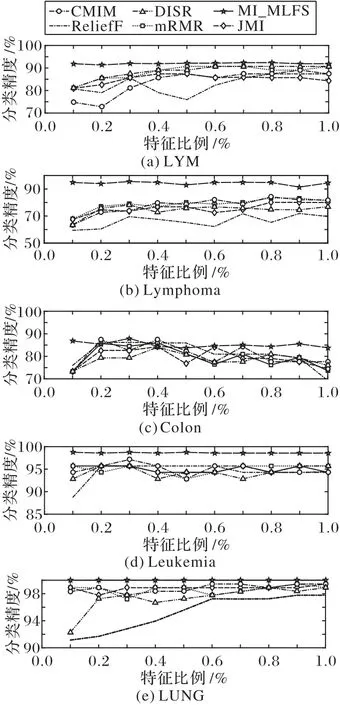
图3 基于SVM分类器的小样本高维数据集上的分类准确率和所选特征比例Fig.3 Classification accuracy and proportion of selected feature subset on datasets with small and high-dimensional samples based on SVM classifier

图4 表示当使用CART 分类器时，在LYM、Lymphoma、Colon、Leukemia 和LUNG 这5 个小样本高维数据集上，6 种算法在所选特征数相同的情况下，得到的各算法分类准确率的结果。其中，横坐标表示依次递増的所选特征子集比例，纵坐标表示平均分类精度。根据图4的结果可知，相较其他5种算法，MI_MLFS 整体上的分类精度较好。其中，在LYM 和Leukemia 数据集上具有明显优势。在Lymphoma 数据集上，当特征比例为0.6%时，MI_MLFS 具有最好的分类性能。在Colon 数据集和LUNG 数据集上，当特征比例为0.1%时，MI_MLFS 具有最好的分类性能。由此表明，面对小样本高维数据集，MI_MLFS 能够选取一个规模较小，并且分类性能较好的特征子集。

图4 基于CART分类器的小样本高维数据集上的分类准确率和所选特征比例Fig.4 Classification accuracy and proportion of selected feature subset on datasets with small and high-dimensional samples based on CART classifier

4 结语

针对仅选取强相关且低冗余的特征不能得到较好的特征子集的问题，本文提出了一种基于互信息的多级特征选择算法（MI_MLFS）。该算法对特征进行三级选取：在选取强相关特征之后，对次强相关的特征集合进行去冗余，得到低冗余的次强相关特征；最后，根据特征与集合的相关度，在其他特征的集合中选取基于组合的强相关特征。实验结果表明，MI_MLFS 选取了较优的特征子集，有效地提高了分类的准确率。然而，本文算法是基于类平衡的假设，没有考虑到少数类的样本对特征选择算法的影响。今后将进一步讨论不平衡数据的特征选择方法。