基于随机游走的改进标签传播算法
郑文萍,岳香豆,杨 贵
(1.山西大学计算机与信息技术学院,太原 030006;2.计算智能与中文信息处理教育部重点实验室(山西大学),太原 030006)
(∗通信作者电子邮箱wpzheng@sxu.edu.cn)
0 引言
在现实生活中,网络无处不在。例如,在社会学中网络表示人与人之间的关系[1];在生物学中网络可以用于研究生物体内的代谢过程[2-3];除此之外,网络还在物理学[4]、医学[5]、信息科学等方面都有很广泛的应用。网络可以被建模为图,图中的节点表示系统中的各个实体,而边表示为实体间的关系。真实世界网络通常由一系列功能模块组成,具有很复杂的连接模式,其具有的一个非常重要的潜在特征是社区结构(community structure)。通常情况下,网络中的社区内部的节点间连接较为紧密,而社区间节点的连接相对稀疏[6]。社区发现算法可以对网络中的社区进行识别,将网络分成不同的功能单元,以便于更好地揭示网络的隐藏结构。它可以广泛地应用于公众情绪分析、用户流失率预测、商品推荐等。
最近几年,社区发现算法被广泛地提出,引起了研究者们广泛的兴趣。研究者利用了生物学、物理学、社会科学、应用数学和计算机科学等不同学科的知识开发了很多社区检测的算法[7]。根据求解策略的不同,可以将这些社区发现算法分为两类:基于优化的算法和基于启发式的算法[8]。其中,基于优化的算法是设置一个或多个目标函数,然后不断地对这些目标函数进行优化,直到得到最优解,其代表性的方法是谱聚类方法[9]和模块最大化方法。谱聚类的方法是将社区检测问题转化为优化二项式的问题,通过拉普拉斯矩阵的特征值和特征向量来对网络进行表示并对网络进行近似最优划分。基于模块性最大化方法是将模块性设为目标函数,并不断地对模块性进行优化,直到模块性达到最大值的方法,如Girvan-Newman(GN)算法[10]、快速Newman(Fast Newman,FN)算法[11]以及BGLL(Blondel VD,Guillaume JL,Lambiotte R and Lefebvre E)算法[12]等。
基于启发式的方法是设置一个启发式规则并利用这个规则来寻找社区的最优分。Palla 等[13]在2005 年提出的派系过滤算法是启发式方法中的一种代表性方法。2007 年,Raghavan 等[14]提出的标签传播算法(Label Propagation Algorithm,LPA)是社区发现算法中最快的算法之一。该算法受到流行病传播的启发,通过节点标签的迭代传播直到收敛来检测社区。由于该算法具有线性的时间复杂度并且过程比较简单,因此可以用于大型网络的社区发现。LPA 首先给网络中的每个节点赋予唯一的初始标签,然后按照随机产生的节点序列对节点进行遍历,将邻域中出现频率最高的标签作为当前节点的社区标签,此过程迭代进行,直到所有节点的标签达到稳定。由于LPA 在社区划分中存在随机过程,使得划分结果有很大的不稳定性,现有很多方法对其进行了改进。为了找到重叠社区,提出了重叠社区传播检测算法(Community Overlap PRopagation Algorithm,COPRA)[15]和基于信息通信的LPA(Speaker-listener LPA,SLPA)算法[16]。除此之外,Barber 等[17]提出了一种基于模块度优化的LPA(modularity-specialized LPA,LPAm)来避免LPA 在运行过程中形成一个大的社区。LPAm 在LPA 中加入约束条件,通过设定目标函数来约束迭代传播的过程,然后将社区模块性值作为另一个目标函数,将社区检测问题最终转化为目标函数的优化问题,但是在算法过程中,最终的结果可能会陷入局部极大值的情况。针对此问题,Liu 等[18]提出了LPAm+对LPAm进行改进,在LPAm 的基础上加入了合并不同社区并使得模块最大化的过程,使得算法可以重新达到一个最大局部极值。Li 等[19]提出了一种两阶段的标签传播算法LPA-S(Stepping community detection Algorithm based on Label Propagation):在算法的第一阶段对节点对之间的相似性进行计算,标签在该节点邻域内相似性较大的节点间进行传播,得到初始的社区划分;在第二阶段将初始划分后的社区看为节点,并进行社区间相似性的计算,合并相似社区,最终所得社区具有最大的目标函数。郑文萍等[20]在2018 年提出了一种基于标签传播的两阶段社区发现算法(Two-Stage community detection Algorithm based on Label Propagation,LPA-TS):该方法定义了节点的参与系数,确定节点的更新顺序,并在标签传播中根据节点的相似性来更新节点标签,得到初始划分;在第二阶段按照参与系数来进行社区的合并,得到最终的社区划分效果。宋琛等[21]在2016 年提出一种基于随机游走相似度矩阵的改进标签传播算法,通过随机游走得到节点的相似度矩阵,并在节点标签更新时,按照相似度矩阵中概率来对节点的邻居节点的标签进行选择和更新。在这些改进算法中,可以看出大部分算法都是只对标签传播算法的标签更新规则进行改进,没有考虑节点初始标签和更新顺序的随机性对算法结果稳定性的影响。本文将综合考虑节点标签的初始化和节点更新顺序对标签传播算法的影响。
针对节点初始标签和更新顺序随机性导致社区发现结果不稳定的问题,本文提出了一种基于随机游走的改进标签传播算法(improved Label Propagation Algorithm based on Random Walk,LPARW),减少了由于标签更新顺序的随机性和在算法初始阶段给每个节点都赋予标签而导致的算法的不稳定性。通过将LPARW 与经典的社区发现算法在真实网络数据集上进行实验比较,发现LPARW 在标准互信息(Normalized Mutual Information,NMI)、调整兰德系数(Adjusted Rand Index,ARI)、模块性等方面都表现得比较好。
基于改进LPA的准确性与稳定性,本文的主要工作如下:
1)通过计算随机游走的位置概率分布来对节点重要性进行一个初始的度量。
2)引入了节点相似性的计算,在随机游走的基础上,确定了种子节点。
3)只给种子节点赋予标签,通过特定的传播规律来对种子节点的标签在网络中进行扩散,使得标签传播算法得到的社区划分结果更加稳定。
1 背景知识
用G=(V,E)来表示一个网络图,其中,V={v1,v2,…,vn}表示网络中所有节点的集合,每个节点由vi表示,n表示网络中的节点数;E={e1,e2,…,em}表示边的集合,即为节点与节点之间的联系。在集合E中的每条边都在集合V中有一对节点与之对应。根据网络中的边是有向的还是无向的以及边上是否有权重,可以将网络分为加权有向图、加权无向图、无权有向图以及无权无向图。本文主要对无权无向图进行研究。通常,使用邻接矩阵An×n来对图进行表示,其中:

无权无向图的邻接矩阵是对称矩阵,即aij=aji。节点的度是复杂网络中节点属性的最重要的概念。一个节点的度即为与这个节点直接相连的节点的数量,而与这个节点直接相连的节点即为该节点的邻域,即NG(vi)={vj|(vi,vj)∈E}。节点的相似性度量有很多种度量方法,可以大致地分为基于局部信息的节点相似性指标和基于全局的节点相似性指标。其中,在基于局部信息的节点相似性指标中最常用的是基于节点之间的公共邻居来对节点的相似性进行度量,如公共邻居(Common Neighbors,CN)指标、Salton 指标[22]和Jaccard 指标[23]等。基于节点之间公共邻居相似性指标认为,任意两个节点之间的相似性取决于其公共邻居数,二者的公共邻居越多,则它们就越相似,从而这两个节点间有连边的可能性也越大。
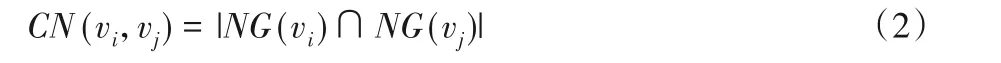
Jaccard 相似性是利用两个节点之间的交集和并集的比例来定义的,比值越高,则证明这两个节点有更高的相似性,由式(3)表示:
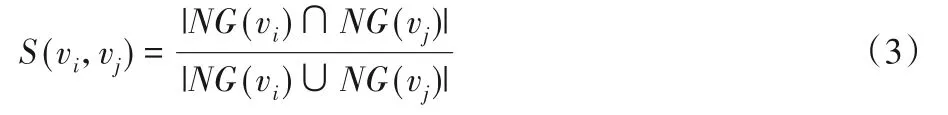
2 基于随机游走的改进标签传播算法
基于标签传播算法的不稳定性,本文提出了一种基于随机游走的改进标签传播算法(LPARW),通过随机游走得到的每个节点的到达概率即为节点的重要性,对重要性进行降序排序从而确定节点的标签更新顺序。根据节点标签更新顺序对节点进行遍历,使用相似性公式对节点之间相似性进行计算,选择出最终的种子节点,对每个种子节点赋予初始的标签。最后,将剩余的节点进行标签传播得到最终的社区划分结果。LPARW 通过确定节点的更新顺序,减少了传统的标签传播算法由于节点标签更新顺序的随机性而导致的最终划分结果的不确定性。传统LPA在初始化阶段对每个节点都赋予唯一的社区标签,在标签传播过程中,一些重要节点的社区标签可能会被覆盖,进而导致社区发现结果不稳定。为了改进此情况,本文算法LPARW 只对选择出的种子节点赋予社区标签,并在网络中进行标签传播。由于种子节点对应网络中的重要节点,其性能比较稳定,因而也提高了社区发现结果的稳定性。
2.1 种子节点的确定
在LPARW 中,考虑到LPA 选择标签时的随机性,将每个节点赋予初始标签进行传播时会增强算法最后划分的社区结果的随机性,而且原始的LPA 中节点的标签更新的次序是随机的,会很大程度上影响社区划分的最终结果。因此,在标签初始化的过程中只为选择的种子节点赋予标签可以减少初始标签的个数,也可以避免由于标签更新顺序不同而造成的社区划分结果的不稳定性,进而扩大有用标签的影响力,提高社区发现的准确率。
马尔可夫聚类(Markov CLustering,MCL)算法[24]是对随机游走进行仿真。MCL 在复杂网络中是一个动态的过程,游走者以一定的概率不断从一个节点移动到另一个节点。根据随机游走方法,如果一个节点作为随机游走结束时到达的节点的概率越高,则意味着这个节点的影响力越大。LPARW 使用随机游走最终的可能位置分布来衡量网络中节点的重要性。在随机游走的过程中,布朗粒子到达其邻居节点的概率由式(4)来表示:

利用式(4)可得到节点的一步游走的概率分布矩阵。对每个节点多步随机游走的可能概率分布进行叠加可得到网络最终的随机游走概率矩阵。若节点的概率分布越高,则证明该节点与更多的节点相似,而一个节点与越多的节点相似,则证明这个节点的重要性越大。每一步的位置分布概率可以由指示向量I和矩阵P的乘积表示。t步之后,游走者位置分布概率可由式(5)表示:

其中,I0为单位向量。将It进行降序排序,可得到更新序列。序列中越靠前的节点作为种子节点的可能性越大;相反,序列中越靠后的节点影响力越小,其作为种子节点的概率也越小。
将所有节点按照影响力大小进行排序,得到节点的更新序列。按照节点的更新序列对节点的标签进行更新,可以减少原始LPA中由于更新序列的随机性而导致的社区发现结果的不稳定性。
基于种子节点的社区发现算法的缺点是需要提前确定种子的个数,而社区发现算法中,社区的个数往往都是未知的,因此种子节点的确定是非常困难的。LPARW 不需要提前确定种子的数量,该算法通过使用相似性度量来对节点的相似性进行度量从而确定最终的种子节点。在本文中使用节点的公共邻居来对两个节点的相似性进行度量:两个节点的公共邻居数越多,则这两个节点结构越相似,属于同一个社区的可能性越大,这样得到的划分结果更符合原来的社区分布,而众所周知,节点的度是刻画单个节点属性的最简单而又最重要的概念之一[25]。无向网络中节点的度被定义为与节点直接有边连接的其他节点的数目。本文给出了节点之间计算相似性的计算公式,由式(6)表示。
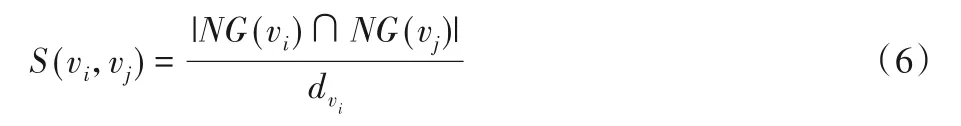
其中:NG(vi)为节点vi的一阶邻居节点的集合;NG(vj)为节点vj的邻居节点的集合;dvi为节点vi的度。
LPARW 中,遍历节点更新序列,将当前节点与更新序列在其之前的节点进行相似性的计算:若当前节点与更新序列在其之前的某个节点是相邻节点,且相似性指标小于阈值,如果该节点的标签为空值,则将序列在其之前的节点选择为种子节点;否则不选为种子节点。在Karate网络中LPARW 选择出的种子节点如图1所示。
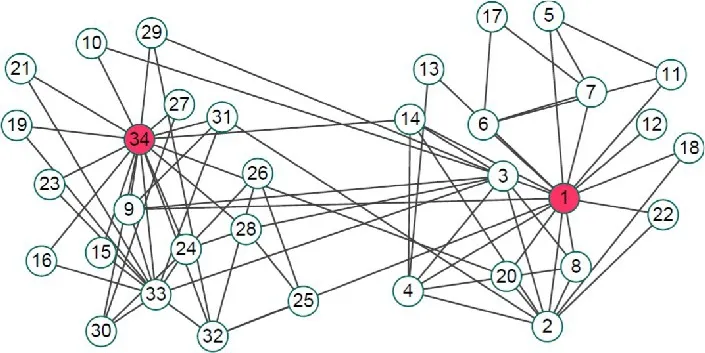
图1 Karate网络上得到的种子节点Fig.1 Seed nodes obtained on Karate network
2.2 标签的更新策略
传统的LPA在标签更新过程根据其邻域中标签数量最多的标签来更新自己的标签。当邻域中最大数量的标签数有多个的时候,则随机选择一个标签作为自己的标签。这样会使得标签产生震荡,导致社区发现结果的不稳定性和随机性,并且在原始的标签传播算法的初始阶段每个节点都有标签,在传播过程中会导致不重要的标签有可能会影响标签传播算法的最终的社区划分的结果。
LPARW 将种子节点的节点标号作为种子节点的标签,其余节点的标签设为空值。在第一次的标签传播的过程中,根据当前节点的标签和种子节点的邻居节点的公共邻域的个数以及该节点本身的度数来决定该节点是否接受种子节点的标签,而不是像传统的LPA将节点标签的重要性考虑为相同的,由此可以减少标签的随机选择而导致的最终划分结果的不稳定性。当节点邻域内满足条件的种子节点只有一个时,则节点选择该种子节点的标签作为节点的标签,若满足条件的种子节点有多个时,则选择出现次数最多的标签作为节点的标签。在对所有种子节点的一阶邻域标签传播完成后,剩余的标签为空的节点根据公式进行标签的更新。
2.3 算法描述
首先,将网络中所有节点的标签都赋为空值;然后,根据随机游走生成的随机序列对这个随机序列进行降序排序,将该序列作为标签传播过程中节点标签的更新序列。根据节点的更新序列来对节点进行遍历。在遍历过程中,将当前节点和在更新序列中位于当前节点前面的所有节点的公共邻域的数量以及其本身的度进行相似性的比较,若有节点vi-1与当前节点vi是相邻的节点且相似性大于选定的阈值,节点vi-1的标签为空值时,则将节点vi-1选为种子节点并将其节点标号作为节点vi的标签,依次循环,选出所有的种子节点并完成种子节点直接邻域的标签传播过程。在第一次标签更新完成后,对剩余标签为空的节点按照原始的标签传播算法的更新标签过程进行更新。以上标签更新过程迭代进行,直到标签达到稳定。下面给出LPARW的社区发现过程。
算法1 基于随机游走的改进标签传播算法。
输入 网络G=(V,E),阈值λ;
输出 网络的划分结果。
步骤1 根据马尔可夫随机游走,生成可能作为游走终止节点的概率分布矩阵,按照式(5)形成节点集合的降序序列B={i1,i2,…,in}。
步骤2 对1 ≤j≤n,令L(ij)={};令t=1,seed={}。
步骤3t=t+1,j=1;如果t>n,转步骤5。
步骤4j=j+1,如果j≥t,转步骤3。
步骤4.1 若边(it,ij)∉E,则转步骤4;
步骤4.2 根据式(6)计算节点it与节点ij的相似性,如果s(it,ij)<λ,则转步骤4;
步骤4.3 如果ij∈seed,则令L(it) ∪{j};
步骤4.4 如果ij∈seed且L(ij)={},则令seed=seed∪{ij},L(ij)={j},L(it)=L(it) ∪{j};
步骤4.5 如果ij∈seed且L(ij) ≠{},则令L(it)=L(it)∪L(ij);
步骤4.6 转步骤4。
步骤5 若网络中存在节点v有多个标签,选择其邻域内出现次数最多的标签作为v的标签。
步骤6 若网络中存在标签为空的节点v,按照式(6)计算v与种子集seed中相邻节点相似性。若s(v,w) ≥λ,则令L(v)=L(v)∪L(w)。若有多个种子节点满足条件,则选择标签出现次数最多的作为自己的标签。如果对节点v不存在满足条件的相邻种子节点,则保持v的标签为空。
步骤7 设当前网络中标签为空的节点集为-V。
步骤8 对-V中节点v,选择其邻居节点中出现次数最多的标签作为v的标签。重复此步骤,直到-V中节点的标签不再变化,得到最终的社区划分结果。
3 实验与结果分析
实验平台是Intel Xeon CPU(3.10 GHz),32 GB 内存,Windows 10 系统,所有算法均采用Python 实验。为了验证LPARW 的准确性和稳定性,将LPARW 在Karate、Dolphin、Football、Polbooks、blogs、Router、rt_ksa、Router_views、PGP 等网络上进行实验,并与LPA、LPAm、LPAm+和LPA-S 等标签传播的经典算法和改进算法进行比较。
3.1 评价指标
此处采用标准互信息(NMI)与调整兰德系数(ARI)对有标签的各算法在有标签网络上的社区发现结果进行评价。NMI被广泛地用于检测社区划分结果的好坏。如果算法社区划分的结果与真实社区结果非常接近,则它的值接近于1,否则NMI 的值接近于0。ARI 是基于两个方法在相同的社区划分下,节点相同的概率。对于一个有n个节点的集合V,B={B1,B2,…,Bk'}表示一个网络划分结果,A={A1,A2,…,Ak}表示网络原始划分。NMI和ARI的定义如式(7)和式(8)所示。
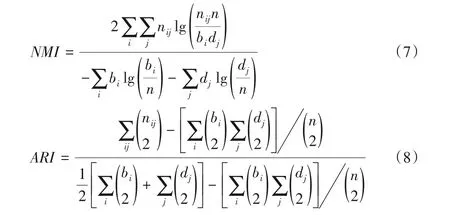
对于无标签数据集,本文采用模块性进行度量。模块度是一种衡量社区划分质量的标准,其基本想法是将随机网络作为零模型,比较所发现社区的模块度与零模型网络模块度的差异,差异越大则社区发现质量越好。模块度Q的定义如式(9)所示。

其中:aij表示邻接矩阵中的元素,若节点i和节点j之间有连边,则aij等于1,否则等于表示随机网络中节点i和节点j的连边数的期望值。
3.2 结果分析
为了验证LPARW 的性能,在空手道俱乐部(Zachary’s Karate Club)、海豚社交网络(Dolphins Social Network)[26-27]、大学生足球网络(American College Football Network)[28]和Polbooks 这4 个带标签的真实网络和blogs、Router、rt_ksa、Router_views、PGP这5个无标签的真实网络上,与基于LPA改进的算法LPAm、LPAm+、LPA-S 和LPA-TS 等比较。数据集基本情况如表1所示。
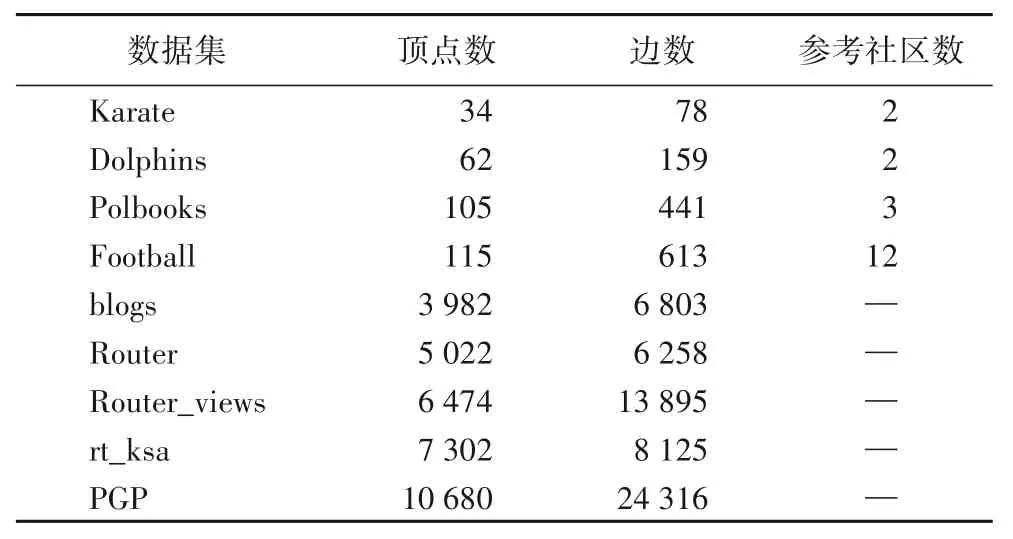
表1 真实网络数据集基本信息Tab.1 Basic information of real network datasets
由于标签传播算法社区发现结果不稳定,因此将本文算法及对比算法在每个网络上分别运行30 次,计算最终所得社区的NMI、ARI 和模块度Q等评价指标的平均值作为最终算法性能,比较结果如表2 所示,其中K表示算法最终发现的社区个数。由于对比算法LPA、LPAm、LPAm+、LPA-S和LPA-TS等各次运行结果所得的社区个数相差较大,无法用具体值描述,表2中用“—”表示。
表2 给出了各个算法在有标签的网络数据集中的实验对比结果。由表2 可以看出,在Karate 和Dolphins 网络中,LPARW 的NMI 和ARI 值达到了1,即算法的社区发现结果与原始的划分完全一致。同时,在其余两个网络中,LPARW 的NMI 和ARI 值也达到了最高,并且该算法发现的社区个数是非常稳定的。因此可以看出,本文算法在有标签的网络数据集中表现良好。

表2 带标签真实网络实验结果对比Tab.2 Comparison of experiment results in labeled real networks
图2 给出了本文算法在Karate 网络上的划分结果。由图2可以看出,LPARW 将Karate网络稳定地划分为两个社区,这与原始的网络划分是一致的。该网络是由34 个节点组成的,网络中的节点表示俱乐部的所有成员,边表示这些成员之间的关系。可以看出,LPARW 的划分结果与原始社区的标签完全一致。
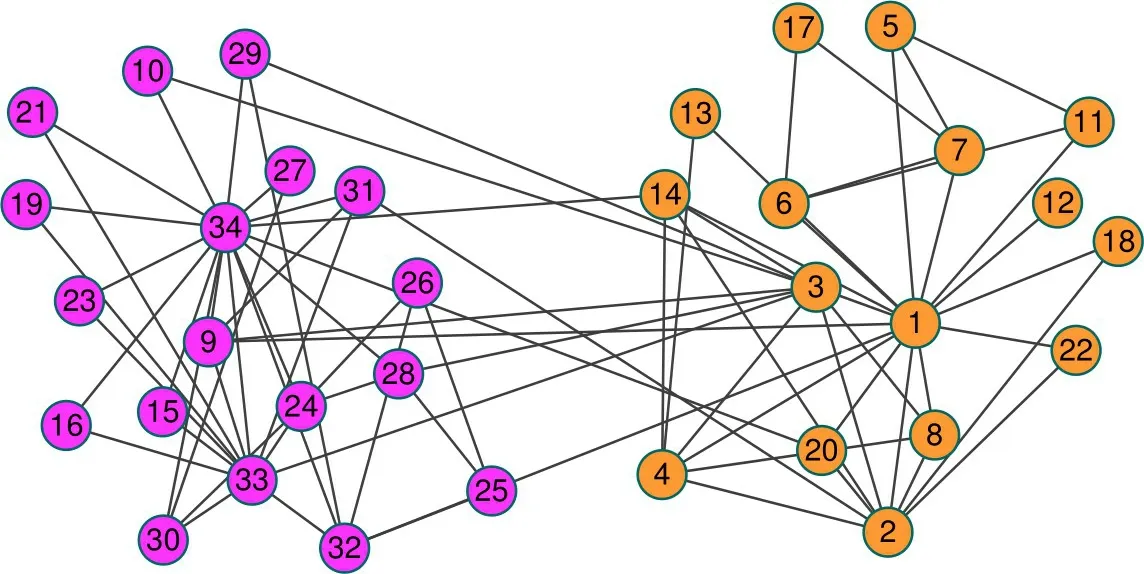
图2 LPARW在Karate网络上的划分结果Fig.2 Division result of Karate network by LPARW
图3 给出了本文算法LPARW 在Dolphins 网络上的划分结果。Dolphins是人们通过对新西兰神奇湾的62只海豚进行长期的观察而得到的网络。其中,节点表示海豚,边表示海豚之间的相互联系。经过长期观察,海豚的活动群体分成两个群体,并且每个群体在不同的活动范围内活动,所以Dolphins网络有两个社区,LPARW 可以稳定地划分出两个社区。由图3 可以看出,LPARW 算法的划分结果与原始网络的社区划分结果是完全一致的。
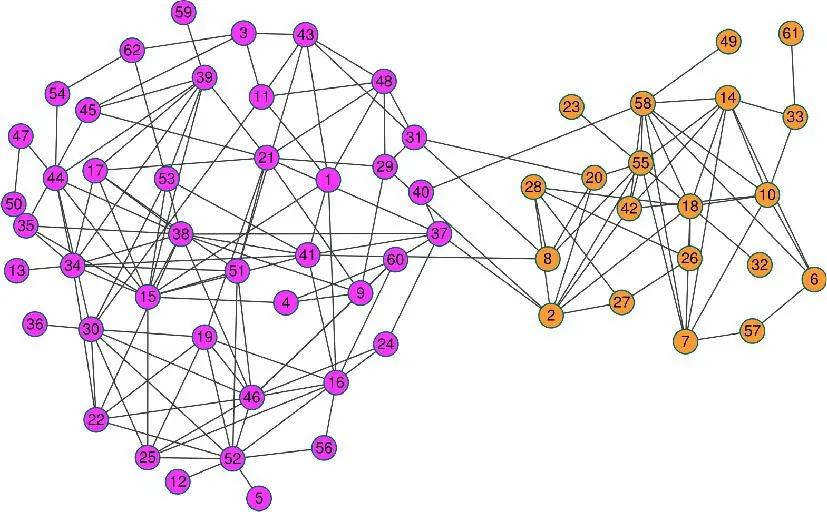
图3 LPARW在Dolphins网络上的划分结果Fig.3 Division result of Dolphins network by LPARW
图4 给出了Polbooks 网络的原始划分,图5 给出了本文算法在Polbooks 网络上的划分结果。Polbooks 网络节点表示在Amazon 在线书店上销售的与美国政治相关的图书,边表示两本图书是否被同一用户购买过。这些图书被分为3 类:“自由派”“保守派”和“中间派”。

图4 Polbooks网络原始的划分结果Fig.4 Original division results of Polbooks network
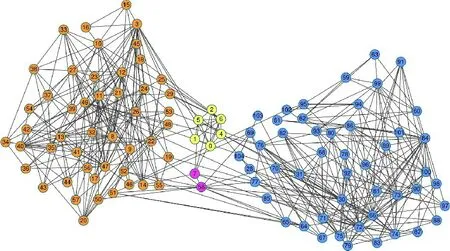
图5 LPARW在Polbooks网络上的划分结果Fig.5 Division result of Polbooks network by LPARW
图6 给出了原始的Football 网络的划分结果。Football 网络是美国高校代表队参加2000 年的赛季比赛的比赛情况。其中,节点表示高校的橄榄球代表队,若两支球队之间至少有过一次比赛的话,则这两个球队之间有一条边。由于每个球队属于不同的联盟,共有12 个联盟,所以,Football 网络会被划分为12个不同的社区。
图7 给出了LPARW 在Football 网络上的社区划分结果。由表2 可以看出,LPARW 相较其他的算法有更高的NMI 和ARI 值,该算法可以将网络的社区稳定地划分为13 个不同的社区。LPARW 相较其他算法的划分结果是最接近原始的划分结果的。
表3 给出了LPARW 在5 个真实的没有标签的网络上与其余5种LPA、LPAm、LPAm+、LPA-S、LPA-TS经典算法在Q值上的对比。可以从表3 中很明显地看出,在大部分的数据集上,LPARW的Q值最高,且社区个数稳定,算法性能最好。
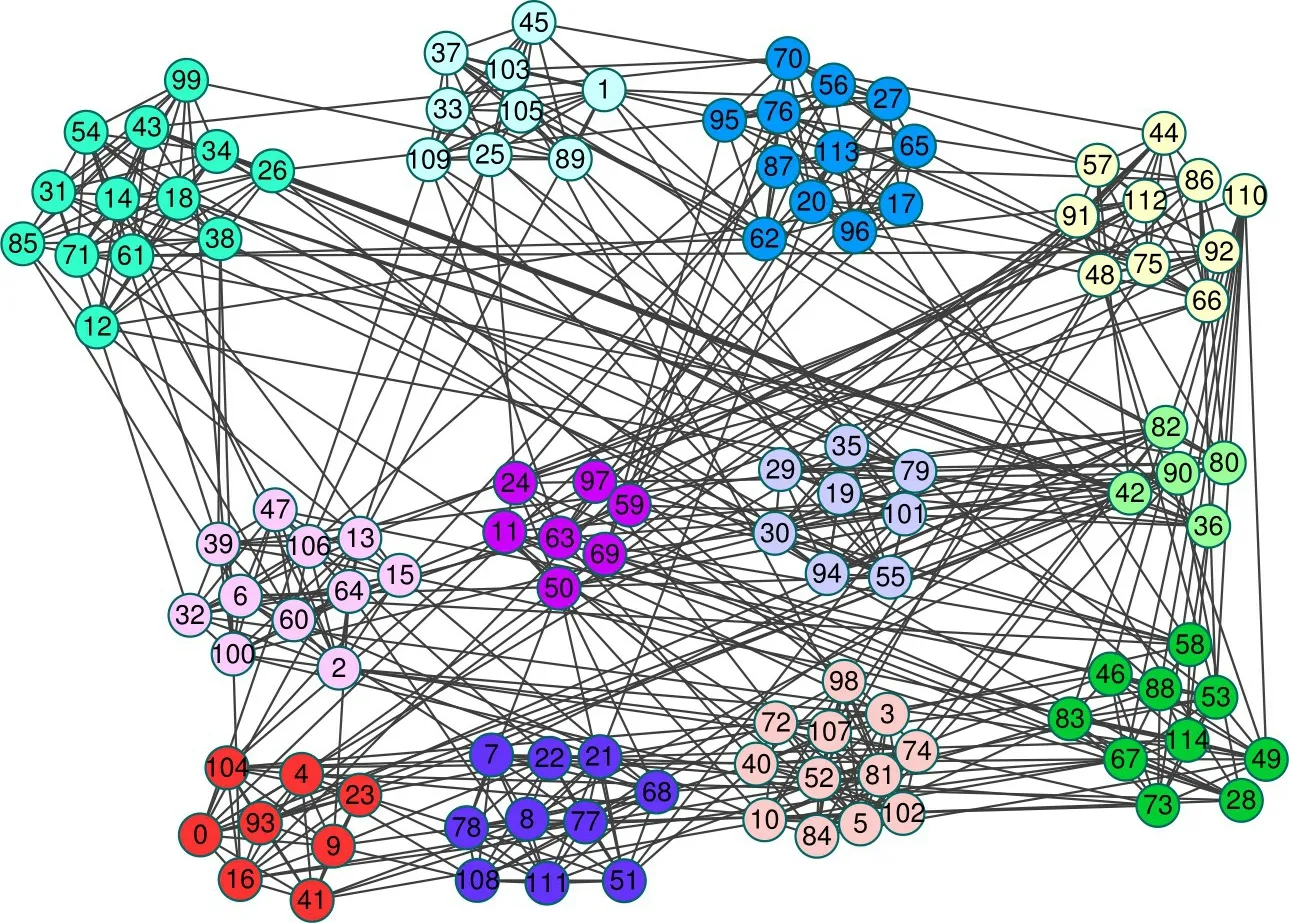
图6 Football网络原始的划分结果Fig.6 Original division results of Football network
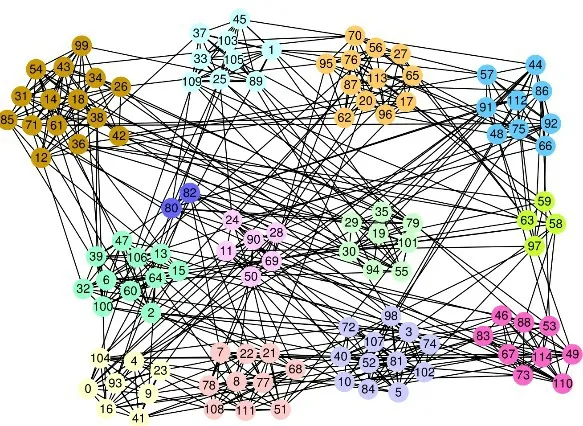
图7 LPARW在Football网络上的划分结果Fig.7 Division result of Football network by LPARW
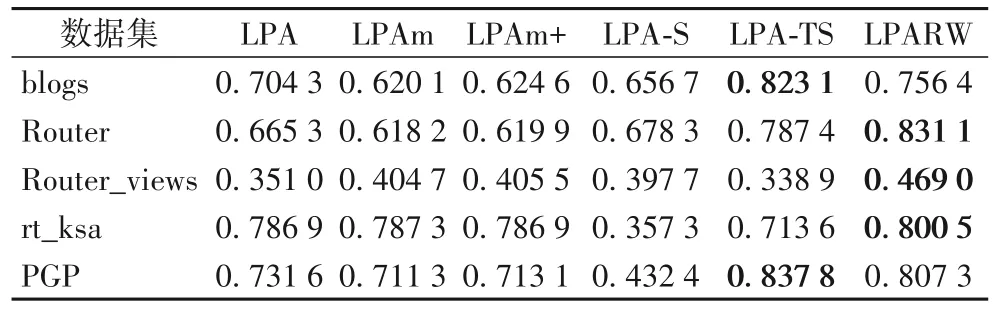
表3 无标签真实网络Q值对比Tab.3 Comparison of Q value in unlabeled real networks
4 结语
本文提出了一种基于随机游走的改进标签传播算法,由于考虑到在原始的标签传播中若给每个节点都分配标签,会增加其余标签对最终社区划分结果的影响,增加算法的不稳定性,所以LPARW 在标签传播过程的赋予初始标签阶段只给影响力大节点赋予标签,然后对其余节点进行标签的传播,这样会增加算法的稳定性,优化算法的最终社区划分的结果。在确定影响力大的节点时,LPARW 使用了随机游走和相似性指标。在生成更新序列时,LPARW 采用随机游走,并对每个节点的可能概率分布进行叠加后生成更新序列,固定了节点标签的更新顺序。在对节点更新序列进行遍历阶段,确定了种子节点及种子节点直接邻域的节点的标签。将剩余的没有标签的节点进行遍历并按照选择邻域节点的标签的最大值来确定标签。通过以上步骤,得到了最终的社区划分结果。通过与经典的社区发现算法LPA、LPAm、LPAm+、LPA-S和LPATS 等在4 个有标签的真实网络数据集以及5 个无标签的真实网络数据集上进行分析比较,实验结果表明,本文算法在NMI、ARI和模块度Q等方面的指标均优于其余的经典的标签传播社区发现算法,表明该算法有很好的社区划分效果。在今后的工作中,对于该算法如何应用于重叠社区将进行进一步的研究。

