无需特征分解的快速谱聚类算法
刘静姝,王 莉*,刘惊雷
(1.太原理工大学大数据学院,山西晋中 030600;2.烟台大学计算机与控制工程学院,山东烟台 264005)
(∗通信作者电子邮箱wangli@tyut.edu.cn)
0 引言
随着信息技术的发展,人们在日常生活中从互联网上获取的信息以海量规模存在,并且持续高速增长[1]。聚类分析利用数据划分来找到数据间的内在联系,能够更快速、更高效、更低成本地收集存储数据[2],已经被应用到机器学习的各个领域中,例如图像分割[3-4]、特征选择[5-6]和降维[7-8]。在过去的几年,研究领域中涌现出许多应用成功的聚类方法,包括层次聚类方法[9]、中心聚类[10]。其中,使用普遍的聚类算法包括k-means 算法[11]、模糊C 均值(Fuzzy C-Means,FCM)算法[12]和最大期望(Expectation Maximization,EM)算法[13]等。诸如此类经典算法,虽然步骤简单且执行效率高,但当聚类样本集的空间为非凸结构时,算法会易陷入局部最优划分中,因此它们缺乏处理复杂簇结构的能力。
谱聚类算法的思想基于谱图理论,将数据聚类问题转化成图划分问题,通过表示出数据的低维非线性形式来实现降维,并且在降维的同时也将这些对象嵌入到欧氏空间,从而在新的空间中进行聚类[14],这种假设对数据的结构分布要求不强,使得它能够处理数据集非凸时的聚类任务[15],克服了k-means 算法等传统聚类方法基于中心聚类而产生的缺点。除此之外,因为对误差数据和噪声数据不敏感,谱聚类方法具有较好的鲁棒性[16]。
尽管谱聚类在很多领域都取得了不错的发展和应用成果,但仍处于发展阶段,还有很多缺陷需要深入研究并进一步改进。首先,谱聚类需要计算图拉普拉斯矩阵的特征向量,所需要的时间复杂度为O(n3),导致当面向大规模数据集时,谱聚类会出现明显的速度缺陷。其次,传统的谱聚类算法存储相似度矩阵需要O(n2)大小的内存空间,如此高的复杂度在处理大规模数据时是无法被接受的,导致它只适用于规模较小的数据集。
为提升谱聚类算法的扩展性,研究者设计出许多可以降低特征分解复杂度的算法来克服计算负担。Fowlkes 等[17]通过改进Nyström方法实现了谱聚类的快速近似特征分解,丁世飞等[18]利用自适应采样技术扩展了Nyström方法,扩展了谱聚类在大规模数据集中的聚类效果。此外,Cai等[19]提出基于地标点的谱聚类(Landmark-based Spectral Clustering,LSC)算法,通过选择地标点并计算数据点与地标点之间的相似度矩阵的乘积得出近似矩阵,虽然利用这种矩阵近似性质可以实现快速特征分解,但该方法的抽样随机性会导致处理大数据集时出现样本点过于集中的问题。
本文利用Nyström 采样思想,设计了一种无需特征值分解的快速谱聚类迭代优化(Fast Spectral Clustering using Iterative optimization,IFSC)算法。该算法克服了传统谱聚类方法处理大规模数据集时的缺陷,通过Nyström思想采样一小部分样本,利用小样本矩阵来构造整个原始相似矩阵,通过乘法更新迭代优化规则来实现聚类。
本文的主要工作如下:
1)基于谱聚类问题的拉格朗日函数,对聚类指示矩阵Y进行求导,得到关于矩阵Y迭代更新的乘法规则,从而避免传统谱聚类的特征值分解。
2)设计了一种不需要特征值分解的谱聚类算法IFSC,该算法根据关于矩阵Y的乘法迭代规则进行更新。具体来说,基于采样的数据点间的相似矩阵E∈Rm×m、采样点和剩余点之间的相似矩阵F∈Rm×(n-m),以及构造的采样小矩阵和原始大矩阵之间的关系对小矩阵进行迭代更新,从而实现对大矩阵的更新,实现了快速谱聚类。
3)在理论上,根据聚类指示矩阵Y构造辅助函数证明了算法的收敛性,使用KKT(Karush-Kuhn-Tucker)条件证明了本文所设计乘法更新规则的正确性。
4)在五个真实数据集上进行了实验验证,实验结果表明,本文设计的快速谱聚类算法与传统谱聚类算法和其他聚类算法相比,处理大规模数据集时,计算时间有所降低;且在处理含有较多噪声的真实数据集时表现优于其他聚类方法(如层次聚类)。
1 相关工作
1.1 谱聚类
谱聚类方法利用图论思想,将数据聚类问题转化成图划分问题,通过对图拉普拉斯矩阵进行特征值分解,得到原始数据在转换后的低维空间中的向量表示。最后,对这些低维特征向量运行k-means算法,从而得到最终聚类结果。
其中,谱聚类的时间复杂度缺陷主要体现在三个方面:相似度矩阵的构建O(n2d)、拉普拉斯矩阵的特征值分解O(n3)和最终的k-means聚类步骤O(nkt)(t为迭代次数)。它的空间复杂度缺陷主要体现在存储相似度矩阵与拉普拉斯矩阵需要的O(n2)上。随着数据大小n的增加,谱聚类的计算复杂度过高,这使得谱聚类方法在处理大规模数据集时,无法发挥更好的性能。
针对以上几点限制谱聚类应用的主要缺陷,可将现有的谱聚类方法主要划分为两种类型:
一种类型是通过约简相似度矩阵的大小来降低样本数量并减小数据集规模,例如Martin 等[20]利用这种思路设计了KASP(K-means Approximate SPectral clustering)算法,优先对数据集使用k-means等方法进行初始化聚类,从而快速地将大部分点绑定到局部的中心点上去,再针对这些中心点进行谱聚类,此时中心点聚类结果即视作绑定于中心点上的普通点的聚类结果。此外,叶茂等[21]改进了基于地标选择的谱聚类(LSC)算法,使用基于近似奇异值分解(Singular Value Decomposition,SVD)抽样方法实现快速的标点采样,克服了抽样地标点效果不稳定的缺点。与文献[14]研究思路不同的是,普通点和中心点的归一化关系是由点与点之间的最短路径来计算,由于保留了图的特性,它更能反映出图的连通状态和点与点之间的相互关系。然而即使在利用这种空间换时间的思路实现改进后,数据稠密图通过阈值限定转化成稀疏图后仍需要O(rnlogn)的时间复杂度,不理想的算法速度限制了它在较大数据集上的聚类应用。
另一种类型是通过选择代表对象来降低样本数据集的规模。这种方法通过在数据集中选择有代表性的对象,利用代表对象构成一个小规模数据集,从而降低可用数据集的规模。然后,利用已有的谱聚类方法划分这些代表对象构成的小规模数据集。最后,根据代表对象所属的类来分配原始数据集中数据所属的类。Chen 等[22]提出了基于子矩阵构造的研究方法,通过利用Nyström 方法从原始数据集中随机选择p个代表,并建立大小为N×p的相似度子矩阵。张涛等[23]改进了子空间聚类算法对高斯噪声敏感的缺陷,使用优化的核范数对系数矩阵的奇异值进行正则化,能够在提高算法准确率的同时,保持其高斯噪声下的稳定性。
由此可见,特征提取是谱聚类方法完成相似度矩阵优化的主要着手点。利用数据点距离的参照采样虽然操作直观简便,但阈值的人为选择和特征空间的映射会导致代表样本和实际样本的差异。此外,使用绑定代表点的方式将图稀疏化会损害数据点集的密度,降低了聚类准确率。如果此时根据数据集的大小增加代表点的密度,依然会产生数据量越大、代表点越多,从而导致算法准确率降低的问题。
本文使用了Nyström 方法进行随机采样间接求解相似度矩阵,使得所有的行和列都能通过映射参与到计算中,最大限度保持聚类结果的准确度。该算法利用选取的子矩阵与原始矩阵的关系来代入乘法更新迭代规则完成更新,从而实现聚类,进一步降低传统方法特征值分解步骤中所需的时间开销。
1.2 谱聚类的基本算法
谱聚类利用谱图理论思想将数据点视作无向图,这里无向图边的权重代表数据点的成对相似性,聚类的目标就是将这些数据点分配到不同的类簇中,使得簇内的数据点之间有较大的相似度,而簇之间的数据点之间的相似度较小。因此,需要构建一个相似度图,即以数据点为顶点、以相似度为权重的一个带权图,从而使构建的相似度图能够反映原始数据集中各个点之间的相似关系。其中,本文公式推导所用到的一些典型数学符号如表1所示。
构建相似度矩阵W常常使用如下的高斯核函数来作定义:

其中,Wij表示数据向量样本xi和xj之间的相似性,使用高斯核函数的时候,需要确定参数σ。那么在相似度图中,数据点聚类问题就转变成图划分问题。划分准则是使划分之后的子图内部的点间相似度尽可能大,不同子图之间的相似度尽可能小。下面介绍利用规范割(Normalized Cut,NCut)划分:将顶点集V划分为两部分A和B,即:A∪B=V,A∩B=∅,构建出相似度矩阵后,将A和B之间的权重之和记作:cut(A,B)=。此时将第i个节点的度定义为。

表1 符号描述Tab.1 Symbol description

谱聚类旨在找到使得规范割目标函数最小的子集A和子集B[24],用类的容量作归一项,兼顾了类的内部和外部的连接。利用以下公式可以计算出最优的NCut值:

Malik等[25]给出归一化的拉普拉斯矩阵的定义:
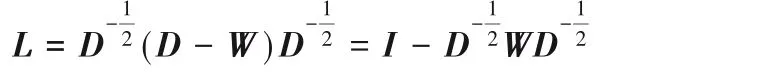
此时L是半正定矩阵,它的特征值区间为[0,2],所以D-1/2WD-1/2的特征值也被限制在区间[1,1]中。扩展到k> 2的多分类问题中,公式可被重写为:

此时有YTY=I,矩阵Y中包含归一化拉普拉斯矩阵L的前k个特征向量。因此,优化公式即可通过标准迹线最小化问题解决,使用文献[25]中提出的归一化谱聚类求解得出指示矩阵Y。在得到矩阵Y作为聚类中心后,利用k-means 算法对指示矩阵Y的行进行聚类,这种算法称为归一化的谱聚类算法。
为了方便在实验中与本文设计的算法进行对比,在算法1中简单描述了谱聚类算法的过程。

2 快速谱聚类框架
2.1 问题描述
谱聚类算法可以视作函数最小化:
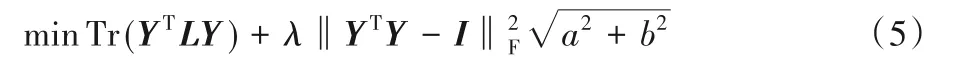
其中:λ是拉格朗日常数;是正交约束项。而式(5)的目标函数是非光滑的,因此不容易由求解拉普拉斯矩阵L的特征值分解来获得有效的分辨率。非负矩阵分解(Nonnegative Matrix Factorization,NMF)算法能够通过松弛技术处理聚类问题,借鉴这种思想,可以放宽离散条件,并提出乘法更新优化的思路来解决特征值分解问题。将非负约束的指标矩阵记作Y,其中Yij> 0。此外,一些传统的谱聚类相关方法将指标矩阵Y放松为正交约束,即YTY=I。文献[26]指出,如果指示矩阵Y同时满足正交和非负,则在矩阵Y的每一行中只有一个元素为正,其他元素为零。因此可以通过添加约束Y>0 和YTY=I来获得文中定义的理想指示矩阵Y,进而利用这种简单有效的方式解决特征值分解问题。考虑以上两个约束的同时放宽离散条件,则式(5)可写为:
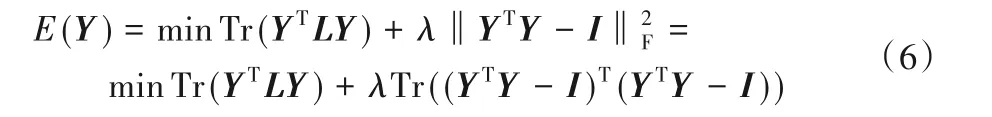
其中Y>0。为了实现损失函数式(6)的最小化,有:

经过上面推导能观察出,式(6)可以视作两部分,即Y+2λYYTY和2λY+D-1/2WD-1/2。因为Y>0,D>0 且W≥0,这两部分都是非负的。为便于描述,将前一个因子表示为Q=Y+2λYYTY,后者表示为P=2λY+D-1/2WD-1/2。根据文献[27]中提出的标准NMF 算法的乘法更新规则,可通过更新Y的方式来使得式(6)中的损失函数最小化,即:

其中,“∘”和“⊘”分别表示Hadamard 乘法和Hadamard 除法(即逐元素乘法和除法),且有:

然后经过一系列迭代后使损失函数收敛。由于在指示矩阵Y的每一行中仅有一个元素为正,其他元素接近零,因此在实现聚类时,可以视作完美的约束指示矩阵,而不像传统的谱聚类中还需要对指示矩阵Y进行松弛和特征分解的处理。
2.2 算法设计和描述
2.2.1 设计模型
为了将谱聚类算法应用于大规模数据集,需要进一步降低计算相似度矩阵的时间和存储复杂度,因此本文在优化模型中选用Nyström 方法来扩展近似有限样本的原始相似度矩阵。
根据Nyström 采样原理,将n个数据点视作两部分:m个随机采样得到的样本点和剩余的n-m数据点。则相似度矩阵W可以写成:

其中:矩阵E∈Rm×m表示m个采样数据点之间的相似度矩阵,它可以用特征分解形式UΛUT来表示,特征向量UUT=I。矩阵F∈Rm×(n-m)表示采样点和剩余点之间的相似度矩阵,而矩阵C∈R(n-m)×(n-m)代表剩余点之间的相似度矩阵。令-U表示W的近似特征向量,由Nyström扩展可得到:

相应的,W的近似矩阵为:
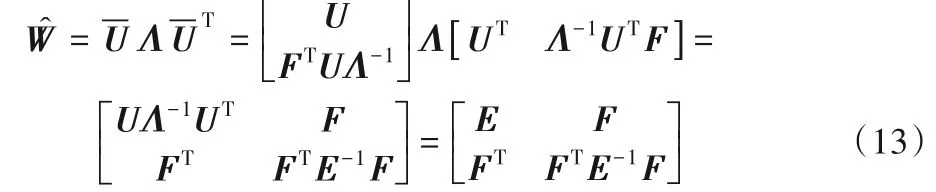
由此可见,Nyström 扩展技术使得矩阵C可以用C=FTE-1F来近似逼近,则W可写为:

由于m≪n,抽样后的剩余点个数很多,而Nyström 技术利用近似逼近降低了计算剩余点间相似度这一步骤所需的时间和空间复杂度。定理1给出了关于矩阵正交特征向量表达式的证明。
定理1若给定一个矩阵E为正定矩阵,且定义矩阵Q=E+E-1/2FFTE-1/2,将其对角化Q=UQΛUTQ,则的正交特征向量为:

证明
1)首先证明V是W的特征向量:
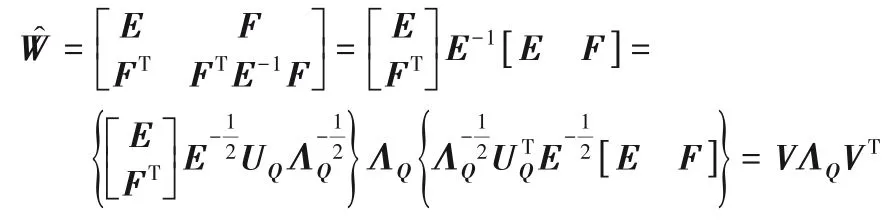
2)然后证明V和VT是正交的。
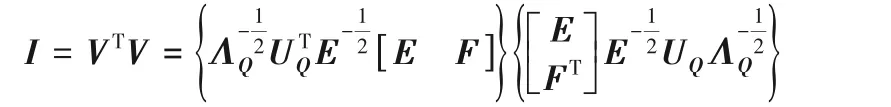
将Nyström 扩展矩阵用于谱聚类,相似矩阵需要作归一化处理,即,其中D是对角矩阵,它的对角线元素Dii等于矩阵的第i行元素和。
文献[17]中给出了节点度的计算方法:

其中:用er=Elm来代表矩阵E的行和;Fln代表矩阵F的行和;fc表示矩阵F的列和;l表示元素均为1的列向量。则不需要求解C=FTE-1F,仅利用d就可以将矩阵E和F归一化:

将式(17)中的E和F代入标准化的相似度矩阵中得到:
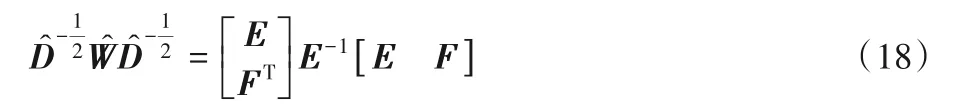
由于矩阵E-1中含有负数元素,故标准化结果也可能是负的。为了保证乘法迭代规则的约束性,需要满足标准化结果非负,即,将矩阵E中的元素拆分为正负两部分并分别记作:E+=(|E|+E)./2 和E-=(|E|-E)./2(其中./代表矩阵中的元素逐个相除),那么此时的E+和E-都是非负矩阵。
将E和F放在指示矩阵Y中,则更新规则中的P、Q可以写作:

此时,矩阵P和Q都是非负的,即可按照式(9)来进行乘法更新迭代。
2.2.2 算法描述
第2.2.1 节中介绍了基于乘法更新迭代的快速谱聚类算法优化模型。本文提出了基于乘法更新迭代思想的快速谱聚类算法,框架具体实现过程见算法2。
算法2 基于乘法更新迭代的快速谱聚类算法IFSC。
输入 数据集X,聚类个数k,参数λ;
输出 指示矩阵Y,聚类结果。
初始化 初始化参数λ并随机生成指示矩阵Y∈Rn×k。
步骤1 利用式(1)计算出数据集样本间的相似度矩阵W,从数据集中随机选择m个样本,通过式(11)构建数据点间的相似度矩阵E∈Rm×m;采样点和剩余点间的相似度矩阵F∈Rm×(n-m),并根据式(16)计算d。
步骤2 利用式(17)更新矩阵E和矩阵F,并根据式(18)计算出近似值用于乘法更新;
当聚类指示矩阵Y不收敛;
计算分母函数Q=Y+2λYYTY;
步骤3 输出指示矩阵Y,并将Y输入k-means 聚类算法得到聚类结果。
传统谱聚类算法可以视作三个阶段:第一步为预处理阶段,对由数据点计算出的相似度矩阵进行标准化;第二步为谱映射阶段,计算相似度矩阵的特征向量;第三部为分组处理阶段,使用常见的分组算法来得到聚类结果。本文的算法利用乘法更新迭代的Nyström扩展思想来实现快速谱聚类,从而降低了前两个步骤所需要的时间损耗。
首先,在输入包含n个点的数据集X=x1,x2,…,xn中,依据已知的相似性度量方法(式(1)),构造数据点集的相似性矩阵W,根据式(18),利用Nyström 方法选取出一部分样本来近似整个相似度矩阵。
由于需要在利用乘法更新迭代思想实现对目标函数的优化之后得到指示矩阵,再完成谱聚类最后的处理或分组步骤,但是从式(16)中可以看出,E-1中可能含有负数元素,使得可能为负。而设计条件的迭代规则中要求满足非负约束性,因此在处理数据时,将矩阵E-1中的元素拆分为正负两部分并分别记作:E+=(|E|+E)./2 和E-=(|E|-E)./2,那么此时二者都是非负矩阵。其次,由于中的大部分元素是正的,则近似值中的大部分元素也为正,此时可以将近似值中的负数元素视作噪声,直接记作零元素处理。因此在公式中满足P>0和Q>0的条件,即能按照更新规则进行后续计算。
最后对矩阵Y的行向量聚类,使用k-means算法将数据点划分,若第i行被分到第j类中,则将数据点xi归到第j类,从而得到k个聚类簇,输出聚类结果。
3 算法理论分析
3.1 正确性和收敛性
在本节中,参照Ding 等[28]的思想,通过不同的对象和辅助函数来证明所提算法的正确性和收敛性。
KKT条件是非线性规划最佳解的必要条件。KKT条件将拉格朗日乘数法所处理涉及等式的约束优化问题推广至不等式。为了验证所提算法的正确性,需要引入满足KKT 互补条件的拉格朗日函数:通过将它的梯度设置为零,能够得到一个解必定收敛于固定点的不动点方程。如果可以证明式(10)中的更新规则满足这些定点方程以及KKT 定点条件,则证明了本文所设计的IFSC算法的正确性。
3.1.1 正确性
命题1算法IFSC的正确性。
式(5)中给出了目标函数,如式(17)中所示的更新规则,此时得到的约束解满足规则下的KKT互补条件。
证明 为了解决优化问题,需要引入拉格朗日函数,由于矩阵计算规则,有Tr(AB)=Tr(BA)且Tr(A)=Tr(AT)。则:

其中,拉格朗日乘数λ>0,Tr(YTLY)用于谱聚类,用于实现正交约束,这个函数满足KKT 的互补松弛条件。将梯度设置为零,可得:
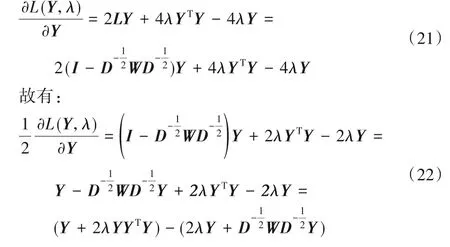
由互补松弛条件得出:
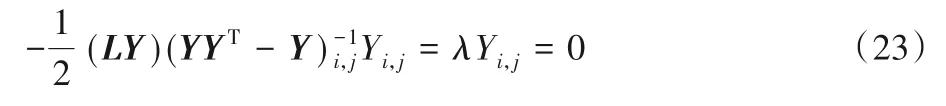
可以看出对于固定点,该等式的解必收敛,且更新规则式(17)中的极限解满足固定点方程,在极限处有:Y(∞)=Y(t+1)=Y(t),其中t为迭代次数。

则式(24)递减到:

当约束区域包含目标函数的原有可行解时,此时加上约束可行解仍落在约束区域内,对应g(x) < 0 的情况,此时约束条件不起作用,故此时可以让λ=0,因为约束条件没有作用。当约束区域不包含目标函数的可行解时,此时加上约束后可行解落在边界g(x)=0 上,所以无论哪种情况都会得到:λg(x)=0。因此,式(17)中具有更新规则的约束解,满足式(23)和KKT定点条件。
3.1.2 收敛性
为了证明IFSC 算法的收敛性,需要构造辅助函数,从而使得在更新规则下,目标函数单调递减。
命题2算法IFSC的收敛性。
在更新规则(式(10))下,式(5)中所示的目标函数单调递减。
证明 将目标函数式(5)记作关于矩阵X的函数:
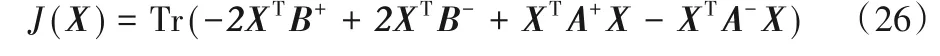
其中,A=YTY,B=XTY。这时,文献[29]中指出需要通过构造辅助函数来证明等式在更新规则式(10)下单调递减,此时辅助函数Z(X,X′)和J(X)应同时满足以下两个条件:

此时,定义:

则由推导可得:

此时J(Xt)单调递减。因此基于这种条件,首先需要构造一个合适的辅助函数Z(X,X′)使得J(Xt)单调递减,其次需要求得其最小值。根据下文中的命题3,在式(31)中定义的是J的辅助函数Z(X,X′),其最小值由式(32)给出。根据式(28),有X(t+1)←X,X(t) ←X′,用A=FF便还原出式(10)的更新规则。
首先构造关于矩阵Y的辅助函数。由于λI是一个常数矩阵,因此在以下证明步骤中将其省略。而需要证明的式(10)中Y的更新步骤恰好是式(28)中所构辅助函数的更新。
命题3
对于满足如下公式形式的函数J(X):

其中所有矩阵均为非负值,则函数:

为目标函数J(X)对应的辅助函数,此处的log 为函数计算值。该辅助函数不仅满足:J(X) ≤Z(X,X′)和J(X)=Z(X,X),且是关于X的凸函数。故有全局最小值:
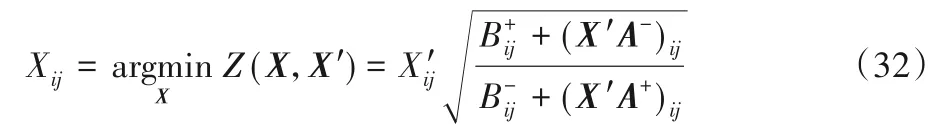
证明
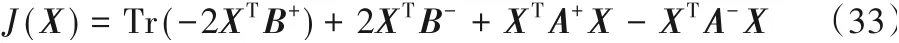
为了找到两个正项的上限,两个负项下限,对于函数J(X)中的第三项,使用命题并令A←I,B←A+,得到一个上限:

对于函数的第二项,由于任意a,b> 0,不等式a≤(a2+b2)/(2ab)始终成立,故可以推导出其边界如下:
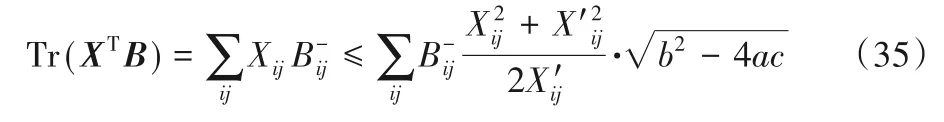
而对于任意z> 0,都有z≥1+logz始终成立。故可以利用这个不等式,继续推导函数J(X)其余两个项的下界:

由式(36)可推导出函数J(X)的第一项的边界:

由式(37)可推导出函数J(X)的最后一项的边界:

汇总以上边界值,就能够验证之前提出的目标式(31)满足J(X) ≤Z(X,X′)和J(X)=Z(X,X)的条件。此时为了求解Z(X,X′)的最小值,对函数进行求导得:
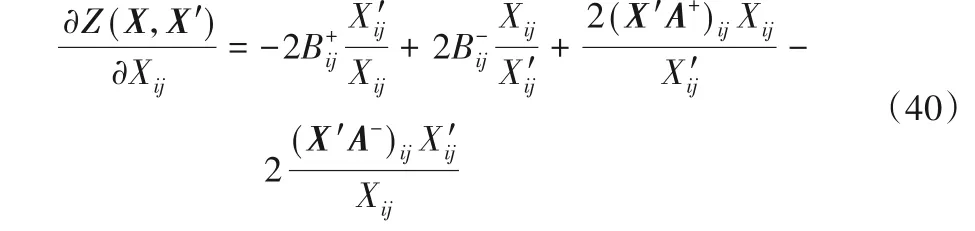
此时二阶导数:

其中:
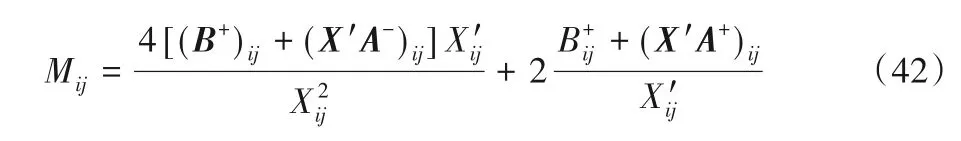
由以上证明可知,辅助函数Z(X,X′)是关于X的凸函数,通过设置求导,如式(40)所示,整理得到关于X的全局最小值即式(32)。
命题4

证明 令Sip=S′ipVip,用一个指定符号来表示不等式左右两端的差异值:

由于A和B是对称矩阵,即:

在出现B=I和S为列向量的特殊情况下,此结果的详细表述在文献[29-30]中。
3.2 算法优势对比
根据乘法更新迭代规则,本文设计的改进算法与传统谱聚类算法相比在时间开销上更有优势。传统谱聚类算法花费了更多的时间来求解拉普拉斯矩阵的特征值分解,而由于利用了乘法更新优化,本改进算法在这个方面提供了更有效的解决方案。同时,由于样本数量和类别的增加,拉普拉斯矩阵特征值分解的时间快速增长,在处理高维数据集时需要花费更多时间。
由于非负约束和正交约束为聚类过程提供了更好的指示矩阵,这使得在后续处理的步骤(例如k-means)中能够得到更好的聚类结果。因此,基于乘法更新迭代的算法在聚类性能方面也略胜于传统谱聚类算法。
4 实验验证
4.1 实验环境
由于文中涉及对算法性能的评估,实验环境可能会对最终结果造成一定影响,因此本文在实验过程中对于实验公平性做了充分考虑。实验过程中使用Matlab语言统一对谱聚类算法的输入和输出接口进行了设定,输入接口为数据样本及其相似度矩阵、相关类数及参数,输出接口为聚类结果。
在实验过程中,提取优化了原作者所提供文献或代码中的算法公用模块,即相似度矩阵的计算、拉普拉斯矩阵的构建及k-means步骤等部分。例如,实验在完成IFSC、SC 算法最后一步的k-means算法步骤中,并没有使用Matlab自带的内置实现,从而避免了当数据量较大时,计算内存不足使用到磁盘的交换区而影响到以秒为精确度的算法评估结果,进行了单独的抽离和统一的调用。在使用k-means算法进行矩阵运算时,统一设定阈值使分批计算的步骤能够在内存中完成;并对算法公用模块进行了优化,从而避免公用模块与内置实现差距太大导致的实验误差。
在准确性评估中的计算都基于式(1)中高斯核函数:

实验中将计算相似度指定为统一的带宽参数σ,且统一设置了各个算法所需要的釆样点数m,低秩估计值统一设定为k。
本文中的所有实验都是在一台8 GB DDR3内存和主频为2.8 GHz 的Intel Pentium CPU 的计算机上进行的,计算机的系统环境为Windows 10 64 位,实验均在Matlab R2014a 中完成。为了防止计算机的读写速度对实验结果造成影响,已经将实验的输入数据在测试前完成读写预热。
4.2 实验数据
为了在实验中对IFSC 算法的聚类性能进行验证测试,实验分别在由UCI(University of California Irvine)机器学习数据库中选取的5 个真实数据集上和3 个人工合成数据集上进行验证。
4.2.1 真实数据集
以下给出实验部分所使用的真实数据集的介绍:
1)Mnist 数据集是一个手写数字数据集,数据集包含60 000个用于训练的示例和10 000个用于测试的示例。这些数字已经过尺寸标准化并位于图像中心,图像为固定大小(28像素×28像素),每个图像都被平展并转换为784个特征的一维numpy 数组。本文实验使用了Mnist 数据集中包含5 000、7 500、10 000、12 500、15 000、17 500 和20 000 个样本的子集。
2)Corel 数据集是图像处理应用任务中广泛使用的数据集,包含巴士、建筑、恐龙等10 个类别的图片,有很好的颜色、纹理、形状等144 个属性特征,利用这些属性特征能够描述并区别每一幅图片的类别。在本文实验中,分别使用2、6 和10类的3个子集来用于评估实验中的算法。
3)WebKB数据集[31]中的示例是从4所大学(康奈尔大学、德克萨斯大学、华盛顿大学、威斯康星大学)数据集主页中下载的网页,这些网页相应的标记分类为学生、教职员工、教职员工、部门、课程、项目以及其他。
4)RCV1 数据集[32]是人工对新闻故事分类整理得到文本分类测试集合,每篇文档都是由一个词频-逆向文件频率(Term Frequency-Inverse Document Frequency,TF-IDF)向量表示,实验中选取了一个RCV1 子集,包含1 925 个文档,包含29 992 个不同的词,包括四个类别“C15”“ECAT”“GCAT”和“MCAT”。
5)Waveform 数据集是常用于分类和聚类任务中的噪声波形数据集,波形数据被分为3类且各占33%,在第40维属性之后的19维为噪声数据,噪声的均值为0、方差是1。
由于真实数据集中含有更多的噪声,且样本边界模糊,因此,在实验过程中调整了部分数据集的大小,表2 中给出了实验中使用数据集的详细信息。
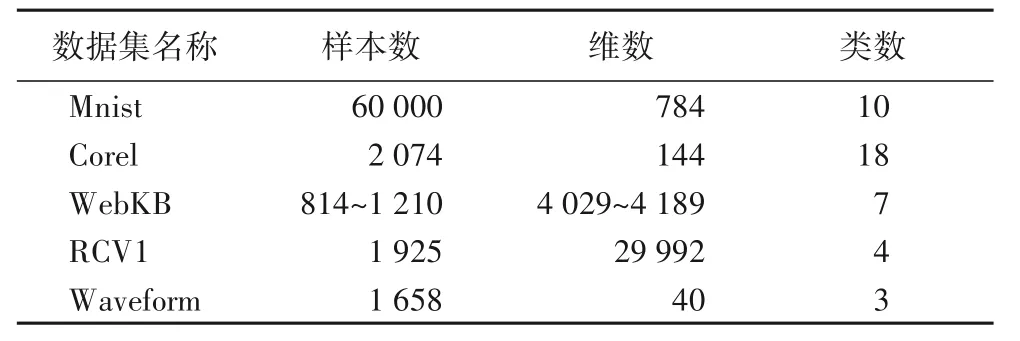
表2 实验中使用的真实数据集Tab.2 Real datasets used in experiments
4.2.2 人工数据集
为了进一步验证算法的正确性,实验中除使用了真实数据集外,还在三个聚类任务中常使用的人工合成数据集[33]上进行了验证,其主要目的是验证IFSC 算法的有效性,即在不需要特征值分解的情况下同样能够达到相应的聚类效果。图1中给出了所使用的合成数据集的流形结构。
根据流形结构将数据集分别命名为环形分布数据集Circle Cluster(CC)、双螺旋结构数据集Two Spirals(TS)和双月型数据集Two Moons(TM)。实验在每个合成数据集中选取了10 000 个样本点并划分为两个类簇。此时在合成数据集,尤其是环形分布数据集CC 和双螺旋结构数据集TS 中,仅依靠数据样本点间距离作为标准的聚类算法就很难得到较好鲁棒的聚类结果。

图1 合成数据集的流形结构Fig.1 Manifold structures of synthetic datasets
4.3 评价指标
使用标准化互信息(Normalized Mutual Information,NMI)来评估不同聚类方法的表现性能,即互信息分数的归一化,用熵做分母将结果调整到0与1之间,由如式(44)来定义:
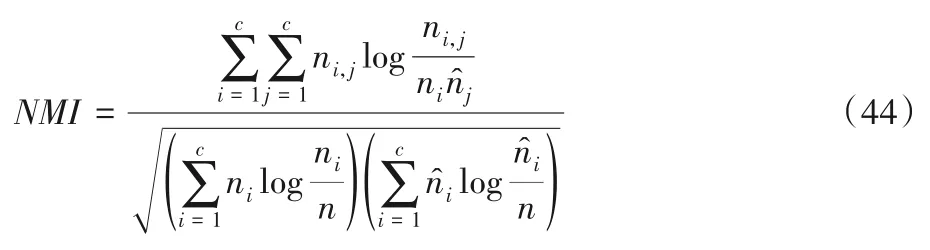
其中,ni、nj、nij分别代表样本属于聚类簇Ci(1 ≤i≤c)、属于类别Lj(1 ≤j≤c)和同时属于两者时的样本数量。NMI 值越大,则聚类结果越好。
4.4 实验过程
为了验证本文所设计IFSC 算法的正确性、准确率和效率,在实验中对以下方法进行比较:
1)使用k-means(KM)聚类算法。
2)使用本文所设计的基于乘法更新迭代思想的快速谱聚类(IFSC)算法。
3)传统谱聚类(SC)算法,即需要特征值分解的谱聚类算法。
4)层次聚类(Hierarchical Clustering,HC)算法。
实验结果除了给出本文算法与传统谱聚类的性能对比,还能得到IFSC 算法相较于常用的基于距离迭代和基于层次分解的聚类算法在进行大规模数据集处理时的性能优点。
4.5 正确性和收敛性
4.5.1 聚类性能比较
在真实数据集上的实验主要用来评估算法正确率和执行性能,实验结果中,需要将速度和准确率两方面结合来综合评价算法的表现;而在人工合成数据集上的实验主要是验证所设计的算法是否符合谱聚类的一般特征。
表3 中展示了不同算法在不同真实数据集上的执行速度和准确率。通过表3 可以看出,本文设计的IFSC 算法与传统的谱聚类(SC)算法相比,极大地降低了算法所需要的时间成本,当选用Corel 数据集,类数Cls=10 时,所消耗的时间仅是SC算法的28.4%,原因是IFSC算法避免了对拉普拉斯矩阵的创建和分解,在处理真实数据集,尤其数据规模较大和维数较高时最有效。考虑到Matlab内置的特征值分解是高度优化的版本,迭代的方法完全是代码,实际性能提升可以更高。另外可以看到,SC 算法虽然在处理WebKB 和Waveform 数据集时,在选用Washington、Texas、Wiscosin 这三个类上进行聚类的NMI 值优于IFSC 算法,但仅增高了约21%,并且可以观察到,在其他四个数据集上的聚类结果指标均不如IFSC 算法有效。结合表3 中的速度对比,证明了不需要特征值分解的乘法迭代算法能够完成谱聚类过程中对数据矩阵的度量和处理。
观察IFSC 算法和KM 算法的速度性能对比可以发现,随着数据集维数的升高,KM算法的运算消耗时间急剧增长。虽然KM 算法在Mnist 数据集上的速度性能表现良好,但在数据集RCV1此类高维数据集上表现较差。正如1.2节中提到的,传统谱聚类算法在处理大规模和高维数据时需要在计算相似度矩阵方面消耗大量时间,从表3 中计算时间的对比可以发现,它的速度性能与KM 相比虽然有所提升,但效果仍然不佳。通过以上比较可以看出,IFSC 算法在处理小型数据集时的计算时间与k-means方法和SC类似。当数据集规模和维数较大时,IFSC 算法的时间开销能少,速度性能更优,这是由于IFSC 算法简化了计算相似度矩阵所需要的复杂步骤,且同时能有效处理谱分解问题。
表4 中展示了不同算法在不同人工合成数据集上的执行速度和准确率。由实验结果可以观察到,使用KM 算法的聚类结果准确性很低,这是由于KM 方法是通过将距离最近样本分配给最近的聚类中心,这种忽略数据全局分布的特点会导致它在处理流形数据集时的聚类能力有限。此外,可以观察到,HC算法在处理合成数据集时能表现出相对较好的聚类性能,因此更适用于处理边界清晰的合成数据;但由于对含噪声和模糊样本边界的数据较敏感,在处理真实数据集时表现不佳。
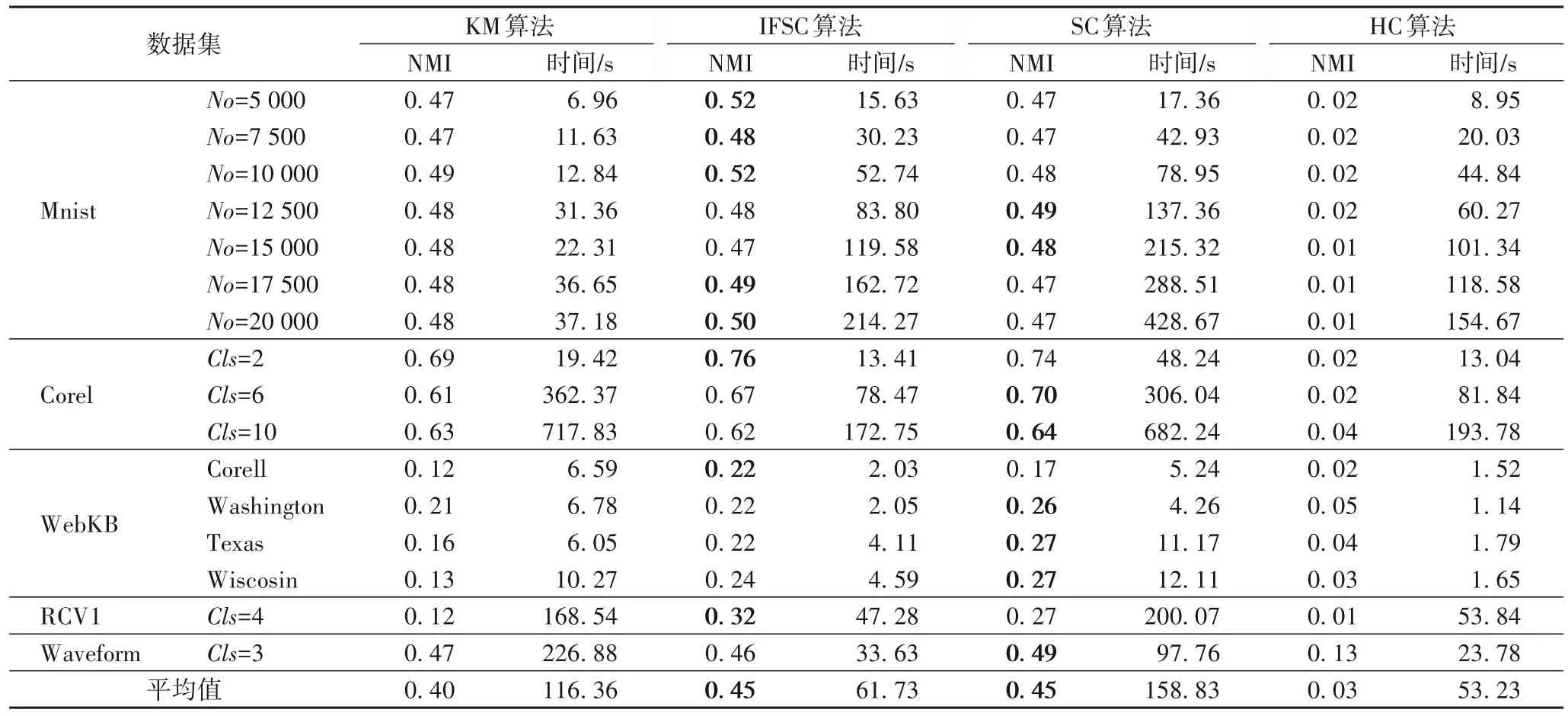
表3 真实数据集的聚类结果Tab.3 Clustering results on real datasets

表4 合成数据集的聚类结果Tab.4 Clustering results on synthetic datasets
其次,从表4 中可以看出,IFSC 算法在TM 数据集上结果较好,但是在CC 和TS 数据集上则需要更多的迭代才能获得更好的结果,这是因为CC 和TS 数据集符合流形分布。尽管如此,在相同精度下,IFSC 相较于传统SC 方法在处理现实任务中更有效。本文中的IFSC 算法利用基于指示矩阵的乘法迭代完成聚类,验证结果表明可达到与传统谱聚类相当的聚类效果。
4.5.2 计算时间比较
为了比较IFSC算法的速度性能,在数据集Waveform 上进行了实验验证。计算时间主要受到迭代次数、采样间隔、样本维数和样本大小的影响,因此在实验过程中控制变量,将迭代次数设置为5 000,采样间隔设置为5,且Waveform 数据集的维度为40,样本个数为5 000。通过保持其中三个变量不变来评估剩余的一个变量,每种方法分别独立运行20 次,参数λ=0.5。实验结果如图2所示。
首先,观察图2 中(a)和(b)的结果可以看出,在其他条件相同的情况下,同k-means 方法和传统谱聚类(SC)方法相比,本文所设计的基于乘法更新迭代的快速谱聚类(IFSC)算法在处理大规模高维数据集时仅花费了一半的时间。
其次,由图2(b)和(d)中的结果分析样本维数和样本大小对算法性能的影响可知,使用k-means方法所需的运行时间随着样本维数大小的升高而快速增加。
此外,从图2(c)和(d)中还可以看出:传统的谱聚类方法对样本量的增加更敏感,这是由于谱聚类方法在计算特征向量这一运算步骤中需要O(n3)的计算复杂度,其中n为样本个数。
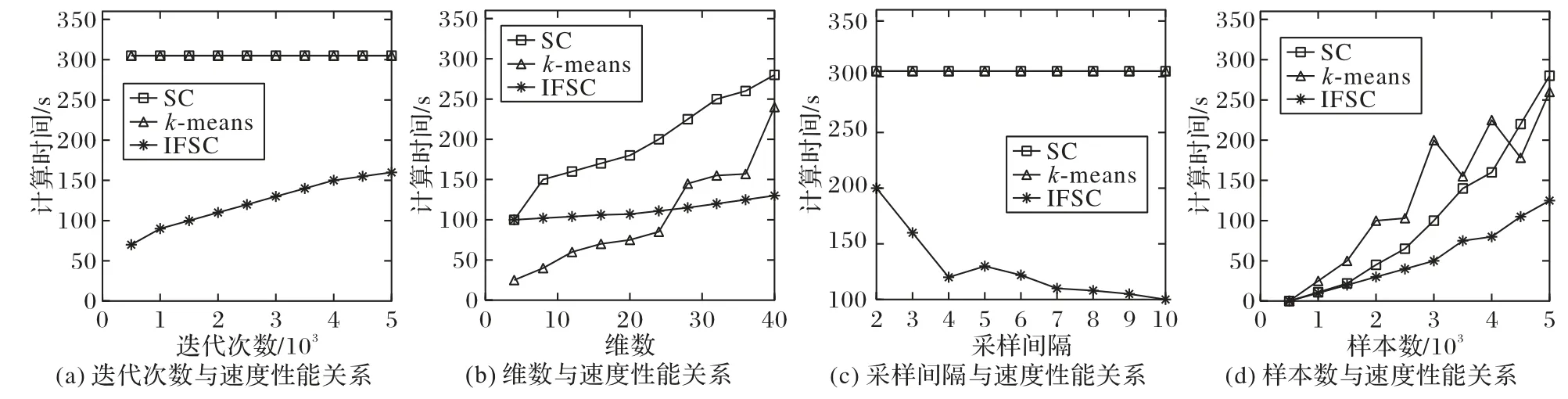
图2 不同方法的运行时间比较Fig.2 Comparison of running time of different methods
5 结语
本文简要介绍了谱聚类技术处理复杂数据集时需要解决的两个主要问题,即相似度矩阵构造和拉普拉斯矩阵的特征值分解。基于乘法更新迭代规则,在聚类指示矩阵Y的基础上设计了一种快速谱聚类优化(IFSC)算法。该算法利用Nyström 方法对数据集随机采样后,根据由子矩阵表示出的指示矩阵完成迭代更新。实验结果表明,所设计的算法在保证聚类精度的同时,提高了传统谱聚类方法的效率,弥补了谱聚类在处理大样本数据集时需要对拉普拉斯矩阵完成特征分解的时间消耗缺陷。接下来工作将使用其他采样方法(如自适应采样方法)来完成算法设计模型的更新迭代,并从理论层面上进一步分析所设计的算法的误差界和泛化界。

