基于ET-PHD滤波器和变分贝叶斯近似的扩展目标跟踪算法

何祥宇，李 静，杨数强，夏玉杰

（1.洛阳师范学院物理与电子信息学院，河南洛阳 471934；2.洛阳师范学院信息技术学院，河南洛阳 471934）

（∗通信作者电子邮箱xyuhe@foxmail.com）

0 引言

目标跟踪技术是一个备受国内外学者关注的研究课题，应用范围十分广泛［1-3］。多目标跟踪（Multi-Target Tracking，MTT）技术研究是目标跟踪技术领域内的一个重要研究分支，多目标跟踪的目的是利用受杂波和噪声影响的传感器测量值估计目标的个数及状态。随机有限集（Random Finite Set，RFS）理论被认为是处理多目标跟踪问题的一种简洁高效的方法，通过把多目标状态集和测量集定义为随机有限集，该理论建立了严谨的最优贝叶斯多目标滤波框架。

在基于RFS 理论的多目标跟踪方法中，概率假设密度（Probability Hypothesis Density，PHD）滤波器［4］是一种很有潜力的多目标贝叶斯滤波算法，它不用复杂的数据关联过程就可以处理复杂环境中的多目标跟踪问题。标准的PHD 滤波器是基于点目标假设的多目标跟踪算法，点目标假设即：在每一个时间步，每一个目标假设只能产生至多一个量测值。与点目标不同的是，一个扩展目标在每一个时间步上可产生多个量测值［5］。因此，应用标准的PHD 滤波器跟踪多个扩展目标会产生不可靠的跟踪结果。

为在RFS理论框架内处理多扩展目标跟踪问题，文献［6］中提出了标准PHD 滤波器的一个扩展版本，称之为扩展目标PHD（Extended Target PHD，ET-PHD）滤波器。目前，ET-PHD滤波器实现方法主要有两种，分别是扩展目标序贯蒙特卡洛PHD（Extended Target Sequential Monte Carlo PHD，ET-SMCPHD）滤波器［7］和扩展目标高斯混合PHD（Extended Target Gaussian Mixture PHD，ET-GM-PHD）滤波器［8］。ET-SMC-PHD滤波器使用随机样本粒子的加权和形式近似后验强度函数，利用聚类及其优化算法实现目标状态的抽取与估计，是ETPHD 滤波器一种通用实现。ET-GM-PHD 滤波器是ET-PHD滤波器在线性高斯假设条件下的封闭解，利用高斯混合函数描述目标的后验强度函数。此外，近期提出的扩展目标箱粒子PHD（Extended Target Box-Particle PHD，ET-Box-PHD）滤波器［9］和椭圆扩展目标箱粒子EET-BP-PHD（Ellipse Extended Target Box Particle PHD，）滤波器［10］是两种新颖的扩展目标跟踪算法，克服了ET-SMC-PHD 滤波过程中使用大量样本粒子近似后验强度函数时存在计算量大的不足，提高了算法的运行效率。

标准的ET-PHD 滤波器需要测量噪声的先验信息，但这种测量噪声的先验信息在许多实际应用环境中都是未知的。测量噪声协方差的显著不匹配会导致ET-PHD 滤波器的目标跟踪性能退化，从而限制了ET-PHD 滤波器的实际应用范围。处理未知测量噪声问题的方法主要有交互多模型（Interactive Multiple Models，IMM）方法［11］、粒子方法［12］和变分贝叶斯（Variational Bayesian，VB）近似方法［13］等。由于具有较低的计算复杂度，VB 近似方法已经成功地被用于基于RFS理论的滤波器中处理未知测量噪声协方差环境中的多点目标跟踪问题［14-17］，并且都取得了令人满意的跟踪效果。

为处理未知测量噪声协方差情况下的多扩展目标跟踪问题，本文提出了一种基于ET-PHD 滤波器和VB 近似的扩展目标跟踪算法。本文根据VB 近似理论及标准的ET-PHD 滤波器，提出了ET-PHD 滤波器的一种扩展版本，并利用相对熵最小化方法给出了其在线性高斯假设条件下的解析实现。本文算法是一种递归的多扩展目标跟踪算法，利用预测和更新过程实现后验强度函数和测量噪声协方差的计算与估计，进而获取相应的目标跟踪结果。

1 扩展的ET-PHD滤波器

定义fk|k-1(xk|xk-1)和gk(zk|xk)分别为目标状态转移函数和测量似然，在线性高斯假设条件下，ET-PHD 滤波器的系统模型可分别表示为下面形式：

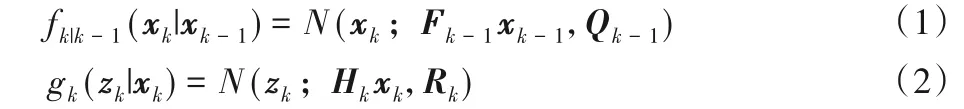
其中：N(x；m，P)表示均值为m、协方差为P的高斯函数；xk和zk分别表示目标状态和测量值；Fk-1和Hk分别表示目标状态转移矩阵和测量矩阵；Qk-1和Rk分别表示过程噪声协方差矩阵和测量噪声协方差矩阵。

根据ET-PHD 滤波器的系统模型，为描述基于VB 近似的ET-PHD 滤波器的公式体系，限定目标状态xk和测量噪声协方差Rk是互相独立的。若定义(xk，Rk)为k时间步扩展目标的增广状态变量，则增广状态变量(xk，Rk)的联合转移函数

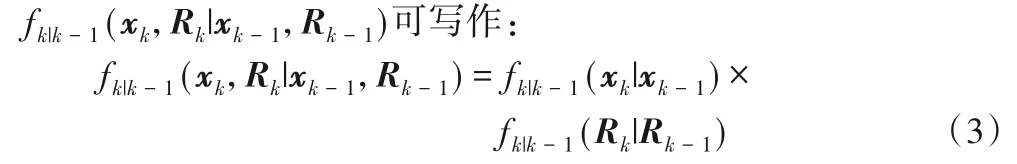
其中，fk|k-1(xk|xk-1)和fk|k-1(Rk|Rk-1)分别表示单目标状态和测量噪声协方差的转移函数。

此外，增广状态的新生目标RFS限定为泊松随机集，定义Db，k(xk，Rk)为新生目标RFS的强度函数，扩展的ET-PHD 滤波器的递归公式描述如下。

假设Dk-1(xk-1，Rk-1)为k-1 时间步的目标联合后验强度函数，则k时间步预测的强度函数Dk|k-1(xk，Rk)可写为：

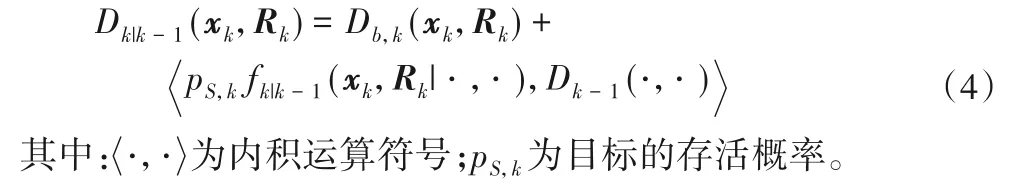
若在k时间步的测量集合为Zk，则联合后验强度函数

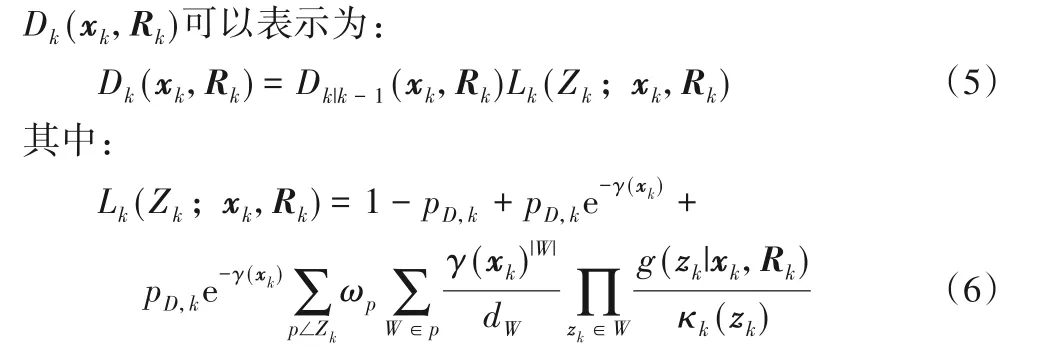
其中：pD，k和κk(zk)分别表示传感器的检测概率和泊松杂波RFS 的强度；γ(xk)表示扩展目标xk产生的测量个数期望值；g(zk|xk，Rk)为测量zk的似然函数；p∠Zk表示划分；|W|表示子集合W中元素个数；ωp和dW分别为划分p和子集W的非负系数。ωp和dW计算式分别为：

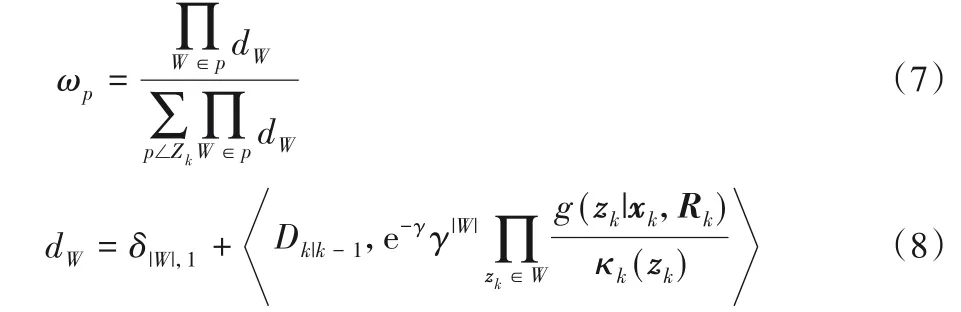
其中：当|W|=1时δ|W|，1=1，否则δ|W|，1=0。

在更新式（5）～（8）中，似然g(zk|xk，Rk)是目标状态xk和测量噪声协方差变量Rk的耦合函数，联合强度函数Dk(xk，Rk)是一种非解析形式。

2 基于VB近似的解析实现

扩展的ET-PHD 滤波器解析实现的一次循环过程包含预测和更新两个过程，解析实现的基础除线性高斯模型之外，还需限定目标的后验强度函数和新目标强度函数为高斯与逆伽马（Inverse-Gamma，IG）混合分布的形式。由此，定义k时间步的新目标强度Db，k(xk，Rk)为下面的函数形式：

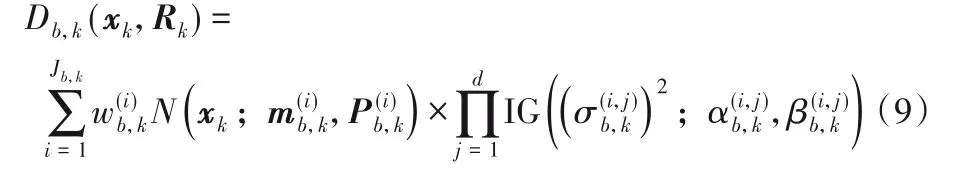
根据上述的假设与定义，扩展的ET-PHD 滤波器解析实现的预测过程和更新过程详述如下。

2.1 预测过程

若k-1 时间步的强度函数Dk-1(xk-1，Rk-1)可表示为下面的函数形式：

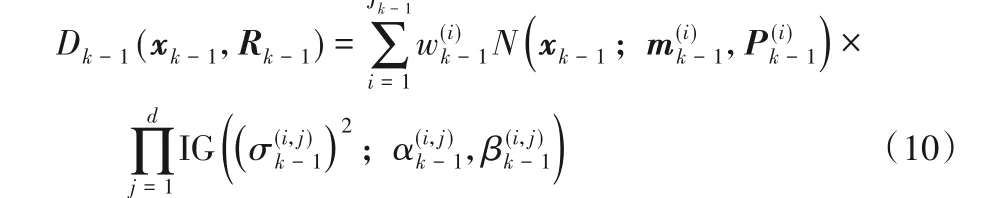
则k时间步预测的强度函数Dk|k-1(xk，Rk)可写作：

其中Db，k(xk，Rk)的表达式与式（9）相同，且有：

式中，ρ(i，j)表示取值范围为(0，1]的衰减因子。

根据式（11）～（17），式（11）描述的预测强度函数Dk|k-1(xk，Rk)可以表示为下面的函数形式：

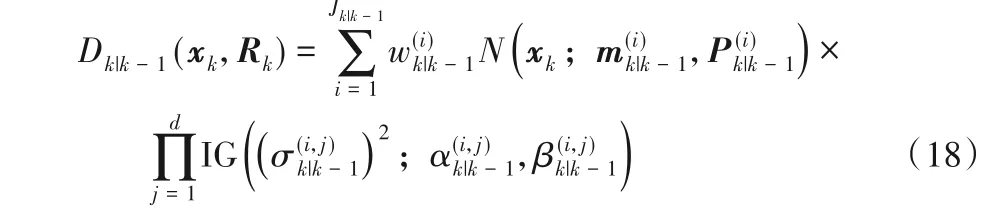
利用式（18）给出的预测的联合强度函数Dk|k-1(xk，Rk)的表达式，预测的测量噪声协方差的计算公式为：

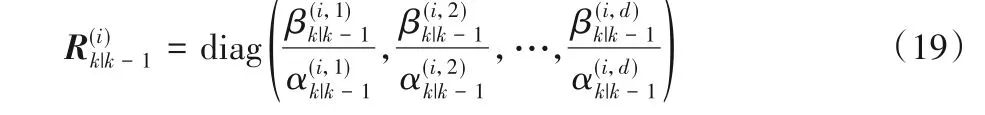
其中diag(⋅)表示构建对角矩阵的运算。

2.2 更新过程

在更新过程，k时间步的测量集利用距离划分方法［8］进行划分，进而实现后验强度函数Dk(xk，Rk)的计算，将式（6）代入式（5）可得：

若k时间步的预测的联合强度函数Dk|k-1(xk，Rk)的函数形式与式（18）相同，将式（18）代入式（22）可得：

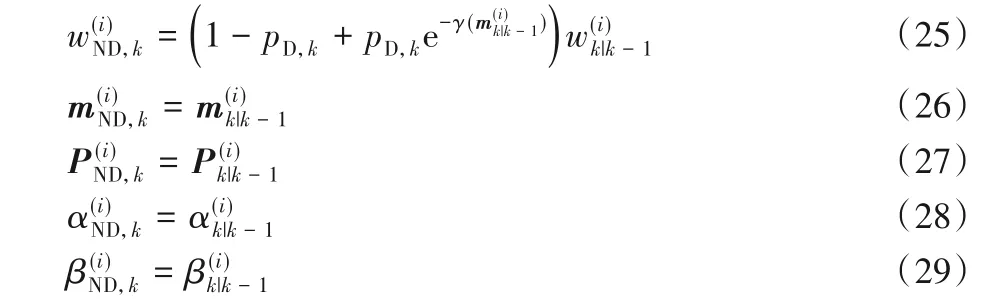
其中：为方便描述强度函数(xk，Rk)的函数表达式，定义如下符号：

其中⊕表示垂直向量连接。

利用文献［13］给出的相对熵最小化结论，联合强度函数，Rk)可表示为：

为获取最优的计算结果，联合强度函数(xk，Rk)表达式中的各参数采用定点迭代算法进行计算，定点迭代算法描述如下：

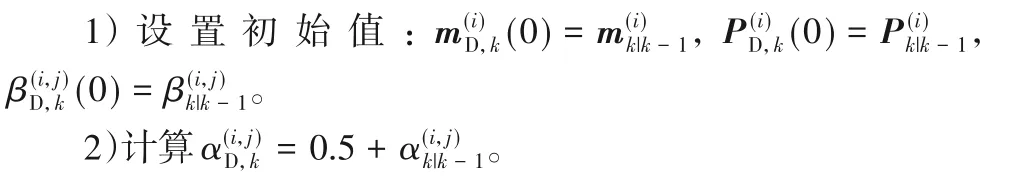
3）利用下面公式进行若干次的迭代计算：

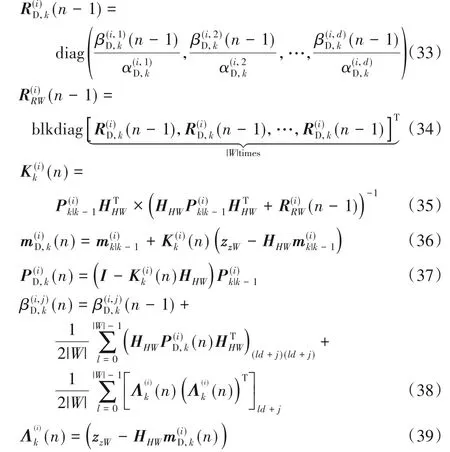
其中blkdiag(⋅)表示构建分块对角矩阵。

定点迭代算法的迭代次数可根据实际需要进行设置，此外式（32）中的其他参数计算如下：

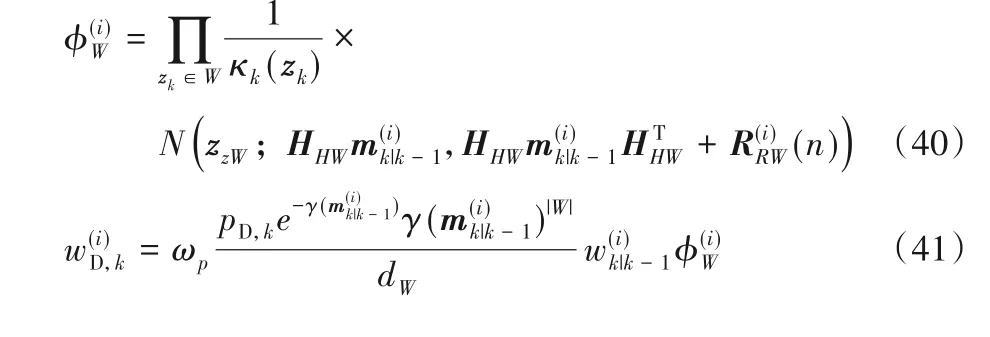
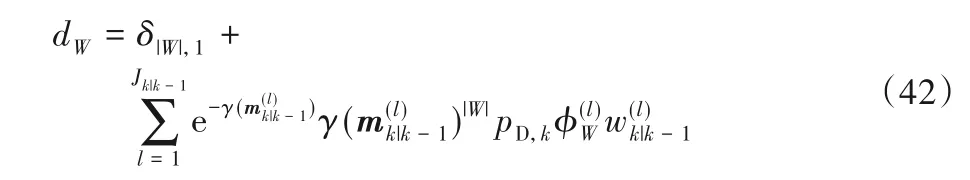
计算得到的强度函数Dk(xk，Rk)用于获取扩展目标的状态和个数，并通过修剪和合并限制Dk(xk，Rk)中高斯与逆伽马混合分量的个数，进而提高运算效率，实现未知噪声环境中多个扩展目标的实时有效的跟踪。

3 仿真与结果分析

利用两个仿真实验验证本文算法的有效性，实验场景设置为包含杂波且目标个数随机变化的一个二维平面。实验环境为：英特尔八代酷睿i5-8250 处理器、8 GB 运行内存、Windows 10操作系统和R2012a版本的Matlab仿真软件。

k时间步的目标状态向量xk由目标位置和速度构成，测量值zk定义为受噪声影响的目标位置信息。仿真实验中采用式（1）和式（2）中描述的目标跟踪模型，模型中的各个参数定义如下：

抽样间隔定义为Δ=1 s，目标的存活和检测概率分别设置为pS，k=0.99 和pD，k=0.99，每个目标产生的测量个数的泊松率设置为γ=10。标准差σq已知，值设置为σq=1.95 m；跟踪过程中标准差σr的值是未知的。仿真实验中用到的新目标强度函数定义为：

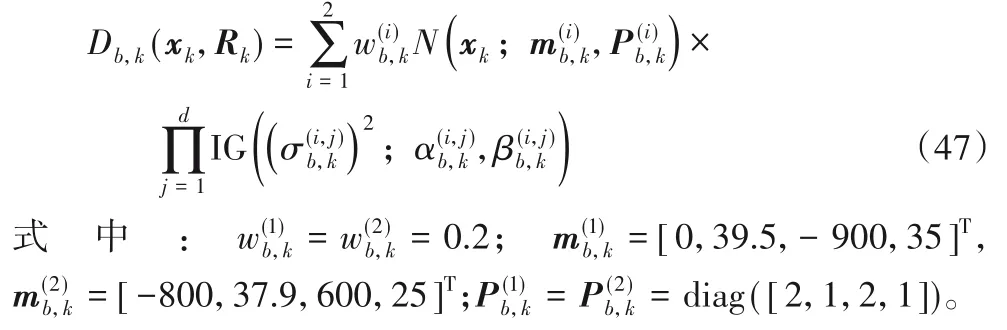
强度函数中高斯分量的修剪阈值为Tw=10-3，合并阈值为U=4，高斯分量个数最大值设置为Jmax=100。逆伽马分布的参数初始值设置为α0=β0=1，退化因子的值定义为ρ=0.9。

不同算法的目标位置估计精度利用最优子模式分配（Optimal Sub-Pattern Assignment，OSPA）距离［18］进行评估，计算公式为：

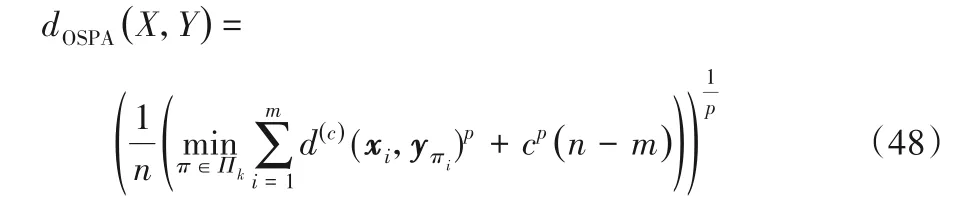
其中：X和Y分别表示目标的真实状态集和状态估计集；p和c分别设置为p=2和c=3 000 m。

仿真场景中设定有三个目标运动，图1 为三个目标的真实运动轨迹。图1所示的仿真场景中，目标1的运动时间设置为50个持续时间步，目标2的运动时间在5到45时间步之间，目标3在时间步10出现。

图1 真实目标轨迹Fig.1 True target tracks

3.1 固定参数实验

本实验中杂波设置为速率为r=10泊松随机有限集，ETGM-PHD 滤波器中的标准差设置为σr=0.65。图2 给出的是一次实验运行中50 个时间步的真实目标轨迹和包含杂波量测的传感器测量值。

图2 真实目标轨迹与测量值Fig.2 True target tracks and measurements

图3为不同算法在一次实验运行中目标的PHD权值。从图3 中可以看出，在17 和22 等时间步上，ET-GM-PHD 滤波器估计的不同目标的PHD 权值存在不同程度的减小，但本文算法的PHD 权值估计却十分可靠。原因是ET-GM-PHD 滤波器使用了不匹配的测量噪声参数进行滤波计算，导致了滤波性能的下降；但本文算法在跟踪过程能够获得合适的测量噪声参数，进而取得了可靠的目标PHD权值。

图3 本文算法和ET-GM-PHD滤波器中不同目标的PHD权值Fig.3 PHD weights of different targets of proposed algorithm and ET-GM-PHD filter

图4给出的是一次实验运行中不同算法在50个时间步上的目标位置估计。从图4 中可以看出，在17、22 和37 时间步上，ET-GM-PHD滤波器未能获取相应的目标位置，原因是ETGM-PHD滤波器中目标PHD权值的大幅下降造成了这种目标位置估计丢失现象的产生，但本文算法在跟踪过程中没有出现目标丢失的现象。

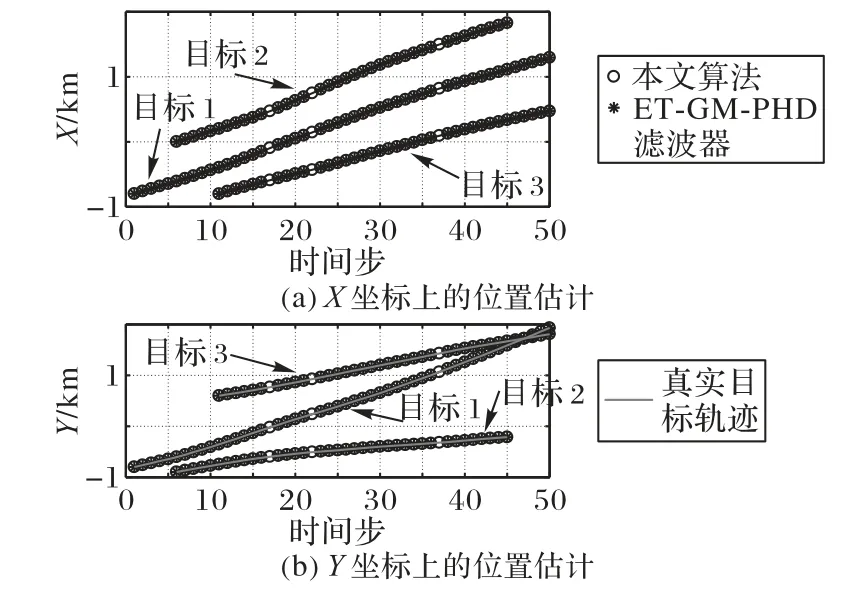
图4 真实目标轨迹与位置估计Fig.4 True target tracks and position estimations

在实验中，不同算法的平均性能从平均的目标个数估计和平均的OSPA 距离这两个方面进行分析，相应的仿真结果分别由图5 和图6 给出。从图5 中可以看出，在11～50 时间步上，ET-GM-PHD 滤波器平均的目标个数估计与目标个数的真实值有着明显的偏差，该偏差产生的原因是ET-GM-PHD滤波器中的不合适的目标PHD 权值估计。通过对比发现，本文算法平均的目标个数估计非常接近真实的目标个数，偏差很小。图6 显示，本文算法的平均OSPA 距离远小于ET-GM-PHD 滤波器的平均OSPA 距离，这种情况在11～50 时间步之间尤为明显。

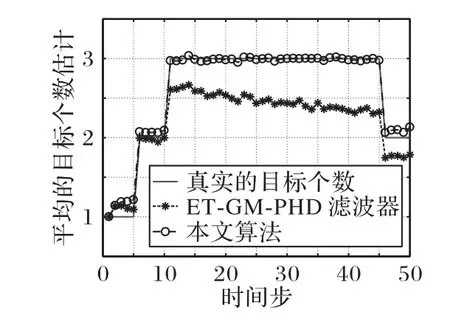
图5 不同算法平均的目标个数估计Fig.5 Average target number estimations of different algorithms

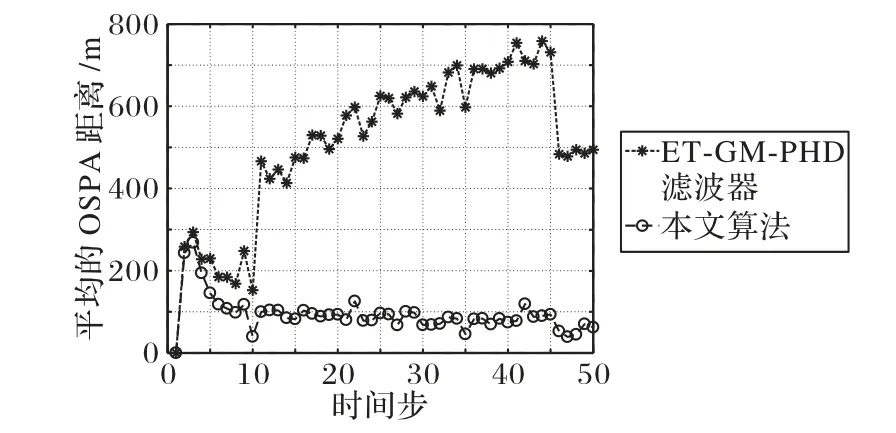
图6 不同算法的平均OSPA距离Fig.6 Average OSPA distances of different algorithms

3.2 变化参数实验

本仿真实验中，不同算法的仿真结果为不同参数取值情况下进行的1 000 次仿真实验中获取的平均值，ET-GM-PHD滤波器中标准差σr取值分别为0.65、0.75、0.95 和1.65 四种情况。首先，目标量测的泊松率固定为γ=10，杂波速率在5到50 之间以等变化间隔5 进行取值，不同算法在不同的杂波速率取值情况下时间上平均的OSPA 距离的对比结果如图7所示。然后，杂波速率固定为r=10，目标量测的泊松率在3到12 之间变化，不同目标量测泊松率时的时间平均的OSPA距离由图8给出。

图7 显示，不同算法的跟踪精度随着杂波速率的增大而下降，但本文算法时间平均的OSPA 距离在不同的杂波速率上总是一直小于ET-GM-PHD 滤波器相应的OSPA 距离。图8显示，当目标量测的泊松率在10 附近取值时，所有算法都可以获取最佳的跟踪精度；但对于所有的目标量测泊松率，本文算法都可以获得精度更好的目标位置估计。根据图7 和图8给出的仿真对比结果可以得到，在未知测量噪声协方差环境中，本文算法能够获得可信赖的多扩展目标跟踪结果。

图7 不同杂波速率下的时间平均的OSPA距离Fig.7 Time averaged OSPA distances with different clutter rates

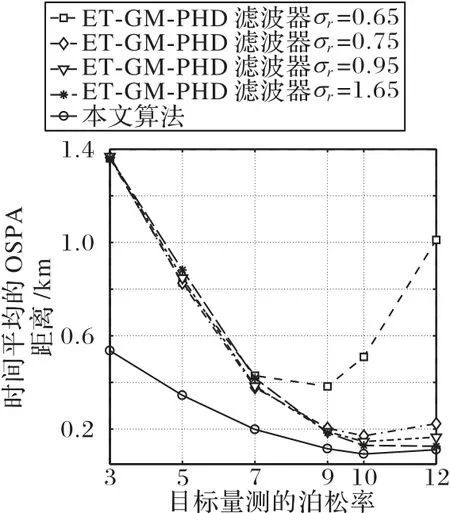
图8 不同目标量测泊松率下的时间平均的OSPA距离Fig.8 Time averaged OSPA distances with different Poisson rates of target measurement

4 结语

为处理未知测量噪声协方差情况下的多扩展目标跟踪问题，利用VB近似理论和高斯与逆伽马混合分布表示的联合强度函数，本文提出了一种扩展的ET-PHD 滤波器及其线性高斯解析实现。仿真结果表明：本文算法能够以可靠的性能跟踪未知测量噪声协方差环境中个数未知且随时间变化的多个扩展目标。在本文研究的基础之上，下一步将研究ET-SMCPHD 滤波器的算法优化方法，以提高ET-SMC-PHD 滤波器的算法运行速度。