面向复杂网络的节点相似性度量*

穆俊芳，梁吉业+，郑文萍，刘韶倩，王 杰

1.山西大学 计算机与信息技术学院，太原 030006

2.山西大学 计算智能与中文信息处理教育部重点实验室，太原 030006

1 引言

自然界中存在大量的复杂网络[1-2]，如社会网络、技术网络、信息网络和生物网络。通常可以用一个图G=(V,E)来描述复杂网络，其中V表示复杂网络中个体集合，E表示个体间联系的集合。在复杂网络的传播与免疫[3]、同步与控制[4]等实际问题[5-8]中，度量节点之间的相似性是一项基础且具有挑战性的工作。

研究者已经提出了各种方法度量节点之间的相似性，如基于邻域节点的相似性指标和基于路径的相似性指标。基于邻域节点的相似性指标考虑了节点之间的公共邻居的信息，如Jaccard 指标[9]和余弦相似性[10]考虑了公共邻居的个数，局部朴素贝叶斯方法[11]、互信息方法[12]和局部相对熵方法[13]考虑了公共邻居节点的权重。复杂网络中节点的邻域信息代表一种浅层局部结构的视图，仅使用节点的邻域信息难以准确地体现节点之间的相似性。基于路径的相似性指标考虑了节点之间的最短路径数目，如Katz指标[14]；或节点之间的到达概率，如局部随机游走[15]、最大熵随机游走[16]等。基于路径的相似性指标使得大度节点成为一般性节点，即许多节点的最相似节点是大度节点。

复杂网络的节点距离分布[17]以一种简洁的方式包含了详细的拓扑信息，例如平均度、接近中心性(closeness centrality，CC）、直径和平均路径长度等，且刻画了网络中局部结构差异。因此，考虑节点的距离分布信息研究节点之间的相似性，可能会更准确地度量节点之间的相似性。本文定义了每个节点的距离分布，并在此基础上采用相对熵提出了一种节点相似性度量方法（similarity measurement based on distance distribution and relative entropy，DDRE）。DDER 方法分为两个步骤：第一步，根据节点之间的最短路径生成每个节点的距离分布；第二步，根据节点的距离分布计算节点之间的相对熵进而得到节点之间的相似性。为了验证DDRE方法的合理性，在6个真实网络数据集上与8 种相似性度量方法进行比较，DDRE 方法在对称性和SIR 模型（susceptible-infectedremoved 模型）中影响其他节点的能力表现较好。

2 相关工作

复杂网络可以用图G=(V,E)表示，其中V是网络G的节点集，E是网络G的边集，令n=|V|表示节点数，m=|E|表示边数。除非特别声明，本文仅考虑连通的简单无向图，即网络中没有重边和自环，且任意两个节点可以通过有限步到达。网络G中节点vi的邻域记作={u|(u,vi)∈E,u∈V}表示图G中与节点vi相邻的节点集合，在不引起混淆的情况下，简记为Ni。节点vi的度=|Ni|表示网络G中与节点vi关联的边数，简记为。Δ(G)和D(G)表示网络G的最大度和直径。

2.1 基于邻域节点的相似性

基于邻域节点的相似性指标考虑了节点之间的公共邻居的信息，即两个节点的公共邻居的信息重合率越高，则这两个节点越相似。Jaccard 指标[9]和余弦相似性[10]（cosine index）考虑了节点之间的公共邻居节点个数并进行标准化。局部贝叶斯方法[11]（local naive Bayes，LNB）假设不同的公共邻居节点对节点之间的相似性具有不同的影响，并通过贝叶斯方法评估节点之间的相似性。互信息方法[12]（mutual information，MI）定义了节点之间的公共邻居的似然函数来度量节点之间的相似性。

2018 年，Zhang 等人提出了局部相对方法（local relative entropy，LRE）[13]。LRE 方法首先寻找节点的局部结构，即当前节点及其邻域节点，并计算局部结构中度分布Pi={pi(k)|1 ≤k≤Δ(G)}作为当前节点的概率分布，然后通过相对熵计算节点之间的差异DKL(Pi||Pj)，进而给出节点之间的相似性，如式（1）所示。

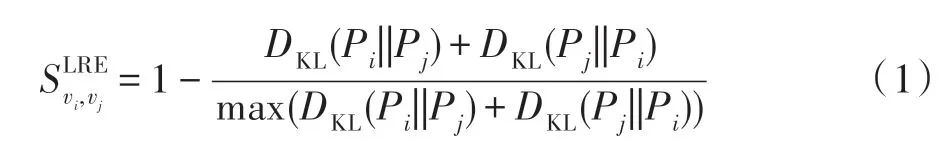
其中：

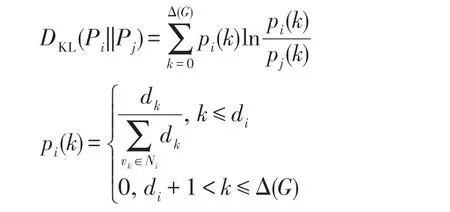
上述基于邻域节点的相似性度量方法主要考虑了节点的邻域信息。然而，邻域信息仅代表一种浅层局部结构，难以准确地体现节点之间的相似性。

2.2 基于路径的相似性

基于路径的相似性指标考虑了节点之间的路径信息，如最短路径的数目、节点之间达到的概率等。

Katz 指标[14]考虑了网中节点之间的所有路径，其定义如式（2）所示。

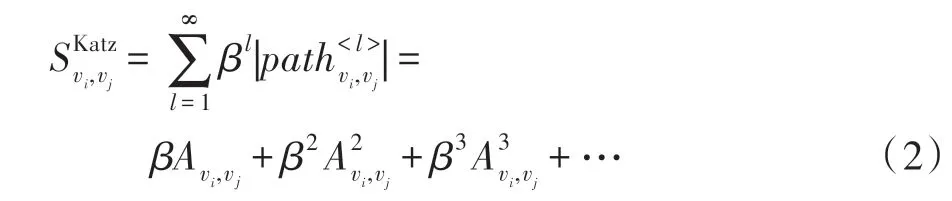
局部随机游走方法[15]（local random walk，LRW）是基于随机游走策略来度量节点之间的相似性，其定义如式（3）所示。

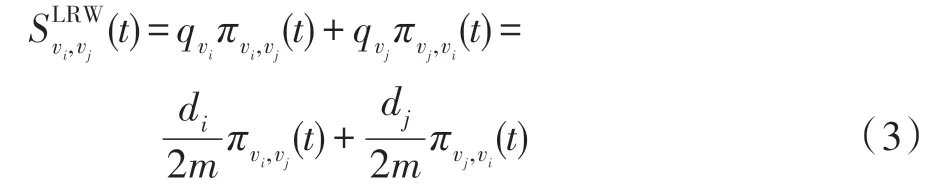
最大熵随机游走方法[16]（maximal entropy random walk，MERW）假设网络中的节点偏向与中心性节点相连，通过最大化熵函数度量节点之间的相似性。

上述基于路径的相似性度量方法使得大度节点成为一般性节点，即许多节点最相似节点是大度节点。

3 基于距离分布的相似性度量

为了避免节点之间的相似性难以区分及大度节点成为一般性节点，本文提出了一种新的节点相似性度量DDRE。DDRE 相似性度量包括两个主要阶段：第一阶段，根据节点之间的最短路径生成每个节点的距离分布；第二阶段，根据节点的距离分布计算每对节点之间的相对熵进而得到节点之间的相似性。

3.1 节点距离分布

复杂网络中每个节点的距离分布为Pi={pi(k)}，pi(k)的计算公式如下：

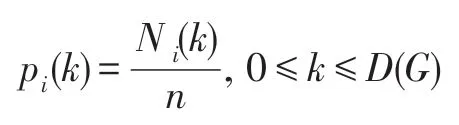
其中,Ni(k)是距离节点vi的最短路径长度为k的节点个数。

以图1 中的实例网络为例介绍节点的距离分布（红色节点代表当前节点，浅绿色、粉色、黄色、蓝色、灰色和亮绿色节点分别代表从当前节点出发经过一步、两步、三步、四步、五步和六步到达的节点）。图1（a）和图1（b）分别展示了节点18 和节点19 与其他节点最短路径的情况。实例网络的直径D(G)=7，即每个节点的距离分布规模是8。根据路径距离长度，节点18依次可到达的节点个数N(i)={Ni(k)|0 ≤k≤D(G)},即：

N(18)={1,4,5,4,4,2,1,0}

由此可得节点18 的距离分布为：

Fig.1 Distance from node 18 and node 19 to other nodes in an example network,respectively图1 在实例网络中节点18 和19 与其他节点的距离

P18={0.05,0.19,0.24,0.19,0.19,0.10,0.05,0}

类似地，节点19 的距离分布为：

P19={0.05,0.19,0.19,0.285,0.285,0,0,0}

复杂网络中n个节点的距离分布{P1,P2,…,Pn}包含详细的网络拓扑信息，如节点的度、第k步到达的节点个数、节点所在的连通分支规模、网络的平均度、网络的直径、节点的接近中心性和平均路径长度等。

（1）节点vi的度

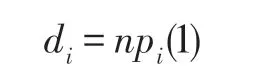
（2）第k步到达的节点个数

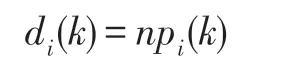
（3）节点vi所在的连通分支规模

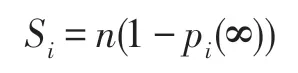
（4）网络的平均度

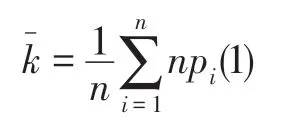
（5）网络的直径

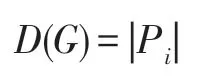
（6）节点vi的接近中心性（CC）

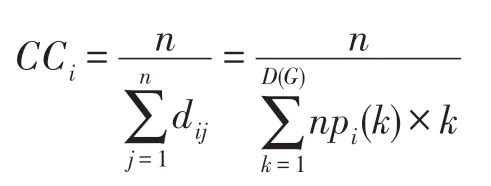
（7）网络的平均路径长度

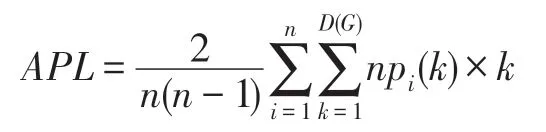
网络的节点距离分布包含了详细的拓扑信息。因此，考虑节点的距离分布信息可以刻画节点之间的结构差异。通过节点的距离分布研究节点之间的相似性,可能会更准确地度量节点之间的相似性。

3.2 节点之间的相似性

信息论中，相对熵也称KL-散度（Kullback-Leibler divergence），常用于度量两个概率分布在统计上的差异。本文使用相对熵度量两个节点距离分布的差异，相对熵越小，则两个节点的距离分布越相似，反之亦然。相对熵的定义如式（4）所示。

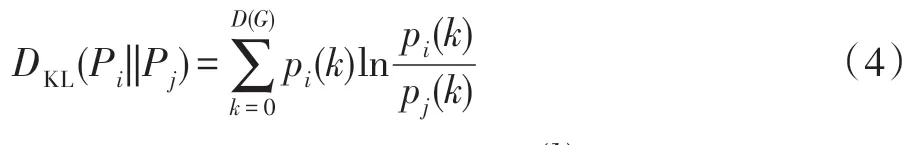
当pi(k)=0 或者pj(k)=0 时，=0 。由式（4）可知，相对熵是非对称的。因此本文对节点之间的相对熵进行转化，即：

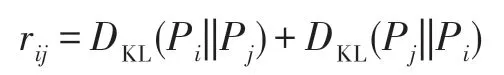
由此定义相似性矩阵S：

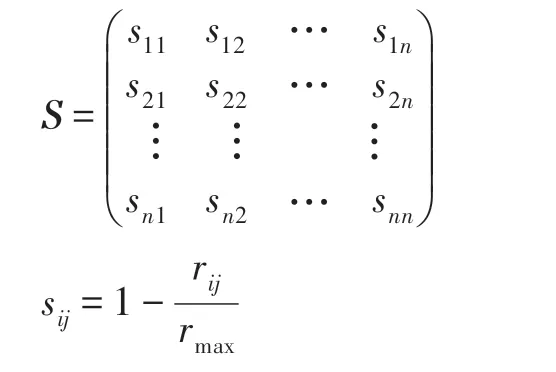
表1 显示了在实例网络中每个节点最相似的3个节点。可以看出与节点2 最相似的节点是17、13、6，与节点13 最相似的节点是17、2、4，与节点17 最相似的节点是2、13、6，即节点2、13、17 具有相似的距离分布。

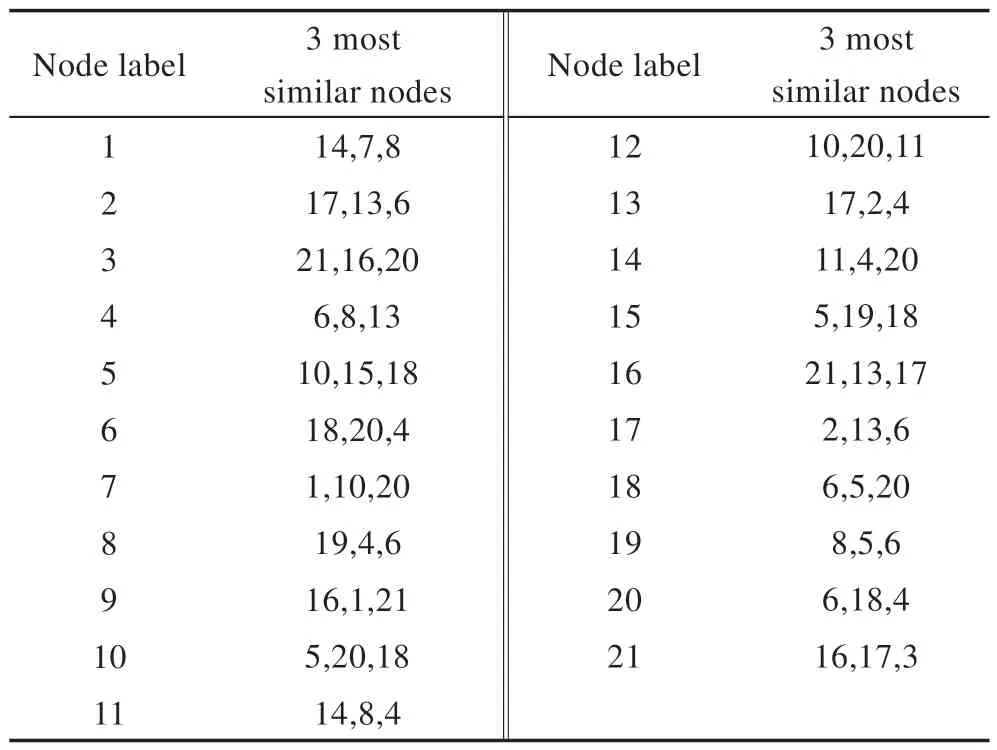
Table 1 3 most similar nodes of each node in example network under DDRE表1 在实例网络中DDRE 方法下每个节点最相似的3 个节点

表2 展示了在实例网络中，LRE 方法和DDRE 方法的对比结果。在LRE 方法下，=1.000 0，=0.9538，=0.946 7。节点18 和节点19 具有相同的度数及相同的局部结构。根据LRE 方法定义的节点局部结构可知，相比于节点10，节点18 与节点21 有相似的局部结构，因此节点18 与节点21 更相似。然而，当进一步考虑局部结构的邻域时，节点18 与节点10 有更为相似的结构。因此，LRE 方法未能较准确地区分节点18 与节点19、21 和10 之间的相似性，且在数值上也未能明显地区分节点18 与节点19、21 和10 之间的相似性。在本文DDRE 相似性度量下，=0.906 3，=0.819 7，=0.944 2。尽管节点18 与节点10 没有共同的一步到达的节点，然而当考虑多步到达的节点时，节点18 与节点10 更为相似。此外，在数值上DDRE 方法很好地区分了节点18 与节点19、21 和10 之间的相似性。

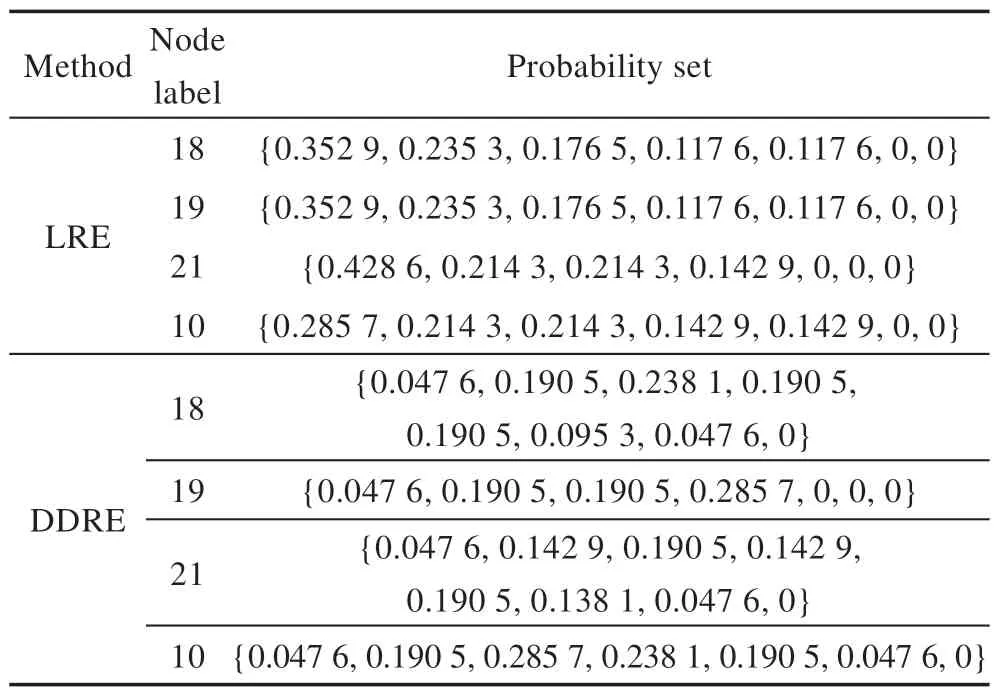
Table 2 Contrast result between LRE and DDRE in example network表2 在实例网络中LRE 和DDRE 方法对比结果

3.3 DDRE 相似性理论分析

本文以ER 随机图和BA 无标度网络为例，分析基于节点的距离分布的相似性对SIR 传播的定性影响。记s(t)、i(t)和r(t)分别为SIR 模型中时刻t的易感人群、感染人群和移除人群占整个人群的比例，则有s(t)+i(t)+r(t)=1。SIR 模型的微分方程描述如下：

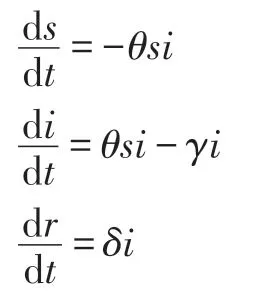
其中，θ为传播概率，δ为恢复概率。则可得到移除人群的稳态值为：

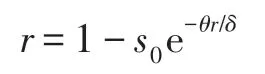
根据ER 随机图构造过程可知，ER 随机图中节点度服从泊松分布，即节点的度数近似相同。设网络的平均度为＜k＞，随机选取一个节点，网络中大约有＜k＞个节点与该节点之间的距离为1，大约有＜k＞2个节点与该节点之间的距离为2，以此类推。因此节点的距离分布：

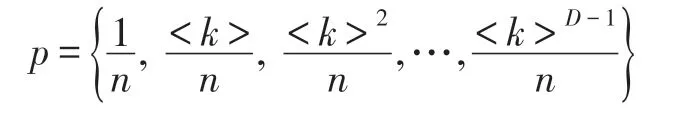
因此，节点之间的相似性难以区分。此外，以每个节点作为初始传播源，即s0=1-，i0=，r0=0，当网络规模足够大时，SIR 模型中移除人群的稳态值为r=1-e-θr/δ，即节点之间具有相似的传播能力。在BA 无标度网络中节点度服从幂律分布，节点的距离分布差异较大，利用相对熵较准确地度量了节点之间的差异性。因此，DDRE 相似性度量在BA 无标度网络中对称性表现较好。

4 实验结果与分析

本章中，3 个经典人工网络和6 个真实网络用于分析DDRE 方法，并选择Katz 指标、局部随机游走（LRW）、最大熵随机游走（MERW）、Jaccard 指标、余弦相似性（Cosine）、局部贝叶斯方法（LNB）、互信息（MI）和局部相对熵方法（LRE）进行比较。

4.1 数据集

本文使用了经典的人工网络和真实网络：ER 随机图、WS 小世界网络、BA 无标度网络、US air lines network[18]、Email network[19]、Yeast network[20]、Soc_CMU network[18]、Bio_dmela network[18]和PGP network[18]。数据基本情况如表3 所示。由复杂网络的小世界特性和“六度分割”可知，节点之间存在较短的最短路径，因此为了降低时间复杂度，Katz 指标中取参数l=3；局部随机游走中同样考虑路径长度为3 的影响。

Table 3 Real network data sets表3 真实网络数据集

4.2 对称性

在本节中，网络中互为最相似的节点比例用于度量不同相似性方法的有效性。若节点vi最相似的节点是vj，且节点vj最相似的节点是vi，则节点vi和节点vj互为最相似的节点。网络中节点之间的对称性定义如下：

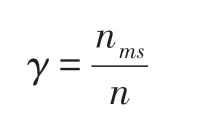
其中，nms表示互为最相似的节点个数。本文使用散点图表示每个节点及其对应的最相似的节点之间的关系。若相似性度量方法准确地度量了节点之间的相似性，则节点之间的对称性γ值较大[13]。此外，在节点及其对应的最相似的节点的散点图中，节点应尽可能地分散在二维平面上，而不是集中在对角线附近，或呈现一条直线，即多数节点与同一节点最相似。

图2 展示了在不同相似性度量在美国航空网络中互为最相似节点的散点图。X-轴代表网络的节点标号，Y-轴代表最相似的节点标号。

图2（a）和图2（b）分别展示了在Jaccard 指标和余弦相似性度量下，节点与其最相似的节点之间的散点图。由图可知，最相似的节点集中分布在对角线附近。Jaccard 指标和余弦相似性是基于节点之间的公共邻居数来度量节点之间的相似性，公共邻居越多，则节点之间越相似，因此最相似的节点分布在对应节点附近，即在散点图中最相似的节点分布在对角线附近。尽管Jaccard 指标和余弦相似性度量下，节点的对称性较好，然而由散点图可知仅考虑一步路径到达的节点难以准确地刻画节点之间的相似性。

图2（c）和图2（d）分别展示Katz 指标和局部随机游走（LRW）度量下，节点与其最相似的节点之间的散点图。由图可知，存在多个节点与同一个节点相似。Katz 指标和局部随机游走是基于路径度量节点之间的相似性，度数较大的节点越容易处于不同节点之间路径之间，因此存在较大的概率使得多数节点与大度节点相似。在美国航空网络中，节点118 是度数最大的节点，节点261 是度数次大的节点，与图2（c）和图2（d）相对应。局部贝叶斯方法（LNB）、最大熵随机游走（MERW）和互信息（MI）度量节点之间的相似性时，同样出现多数节点与大度节点相似，如图2（e）、图2（f）和图2（g）所示。因此，基于路径的节点相似性度量下，网络节点的对称性较差，且使得大度节点成为一般性节点。

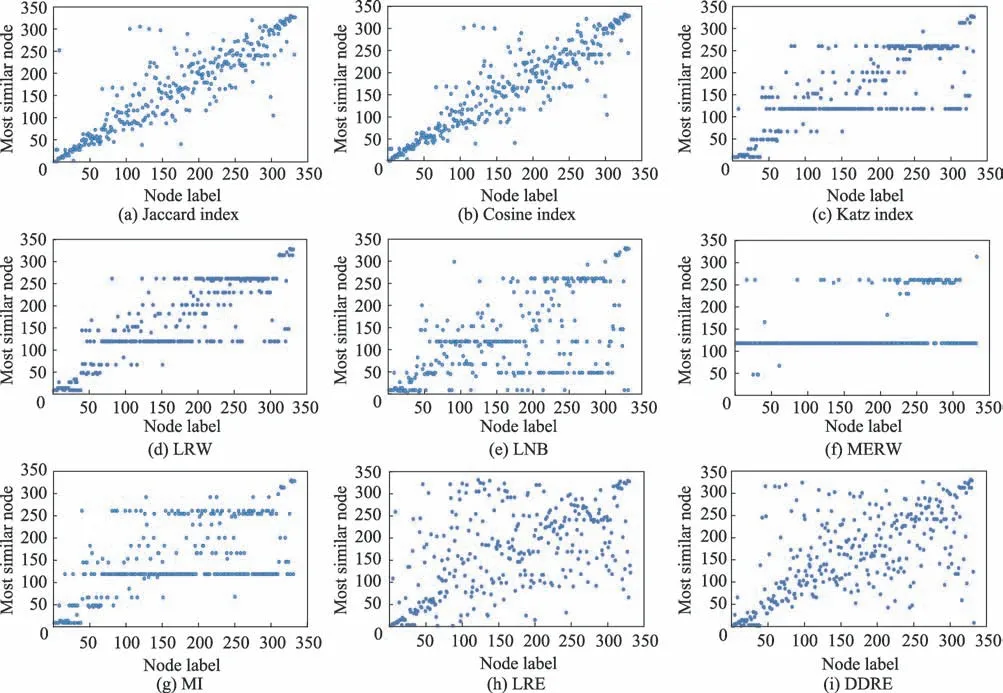
Fig.2 Most similar node of each node in US air lines network图2 美国航空网络中每个节点的最相似的节点

图2（h）展示了局部相对熵方法（LRE）度量下，节点与其最相似的节点之间的散点图。由图可知，节点的最相似节点并没有分布在对角线附近，也没有出现多数节点与大度节点相似。然而，LRE 方法仅基于局部结构（一步到达的节点）度量节点之间的相似性，未能准确地度量节点之间的相似性。此外，当网络规模增大时,节点之间的对称性明显下降,如表4 所示。

图2（i）展示了本文DDRE 度量下，节点与其最相似的节点之间的散点图。由图可知，节点的最相似节点并没有分布在对角线附近，也没有出现多数节点与大度节点相似。DDRE 是基于节点的距离分布来度量节点之间的相似性，考虑了多步路径对节点相似性的影响，同时避免了大度节点成为一般性节点。此外，当网络规模增大时，节点仍然保持了良好的对称性，如表4 所示。

9 种相似性度量方法在Email network、Yeast network、Soc_CMU network、Bio_dmela network 和PGP network 具有类似的性能表现。表4 给出了在不同的相似性度量下节点之间的对称性。本文DDRE 方法表现较好。

此外，本文在人工网络上探索DDRE 相似性方法适用的网络结构。在ER 随机图、WS 小世界网络和BA 无标度网络上与其他8 种方法对比。由表4 可知，DDRE 方法在BA 无标度网络中性能最好。在BA 无标度网络中，节点的度分布服从幂律分布，因此节点的距离分布差异性较大，DDRE 方法可以较为准确地度量节点之间的相似性，即DDRE 方法适用于度量具有幂律分布的网络。

4.3 互为最相似节点的影响力

在本节中，疾病传播模型用于评估不同相似性度量方法的有效性。若两个节点互为最相似的节点，则这两个节点可能有相同的能力影响其他节点。为了验证DDRE 方法的合理性，本文使用经典的SIR模型[21]来模拟网络中的传播，比较不同方法的结果。

在SIR 模型中节点分为三种状态：易感状态（S）、感染状态（I）、免疫状态（R）。易感状态表示节点尚未感染疾病，可以变成感染状态；感染状态表示节点可以传播疾病；免疫状态表示节点不会感染疾病，也不会传播疾病。当网络中节点成为感染状态，则该节点以概率θ感染其邻居节点，且以概率δ恢复成免疫状态。当网络中不存在感染节点时，该过程结束。本文取感染概率θ=0.3，恢复概率δ=1。

在SIR 模型中，将每个节点作为初始传播源，即当前节点处于I 状态，其余节点处于S 状态，以θ=0.3，δ=1 在网络中传播，直到没有I 状态的节点停止。在传播过程中记录每一步感染节点的比例和免疫节点的比例，并计算节点与其对应最相似的节点在每一步的差异，其差异值定义如下：

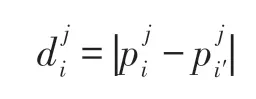
其中，i表示当前节点，i′表示节点i最相似的节点。表示节点i在第j步是网络中处于感染状态的节点比例（或处于免疫状态的节点比例）。表示节点i′在第j步是网络中处于感染状态的节点比例（或处于免疫状态的节点比例）。网络中所有节点在第j步时的方差为：

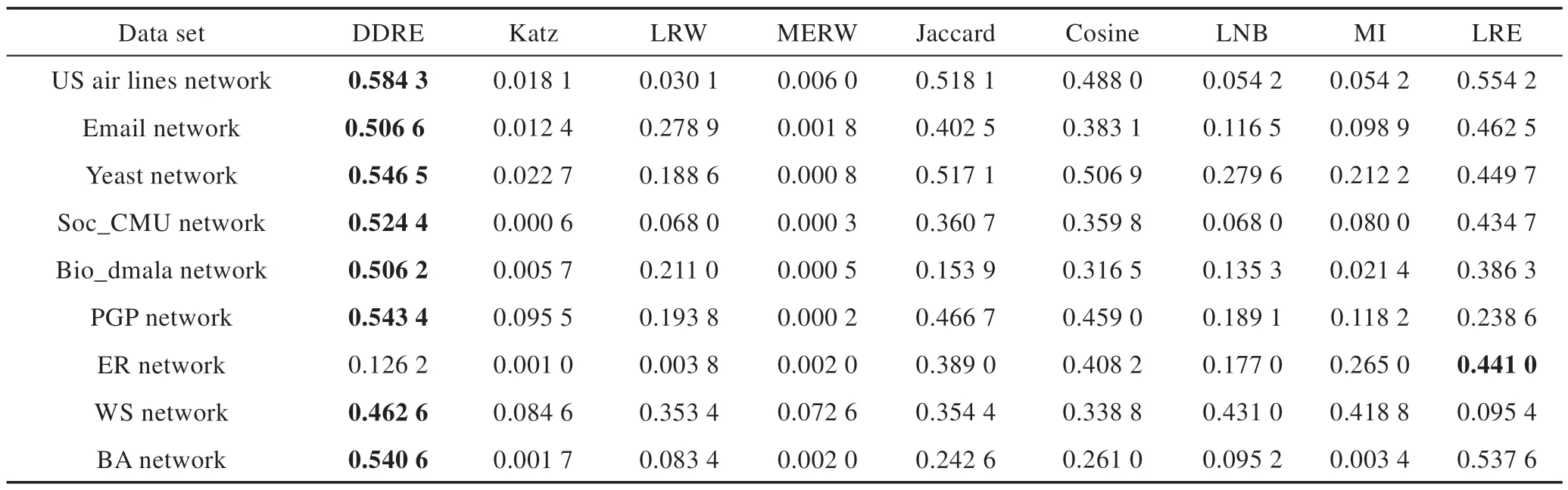
Table 4 Symmetry of nodes under each method表4 每个方法的互为相似性节点比例

在实验过程中，将每个节点作为初始传播源并记录传播过程中每一步的感染比例和恢复比例。本文取100 次的平均作为最终的结果。图3 展示了在不同的网络中，不同相似性度量方法下每一步的感染方差。X轴表示传播的步数，Y轴表示对应步数下所有节点的感染方差。图4 展示了在不同的网络中，不同相似性度量方法下每一步的免疫方差。X轴表示传播的步数，Y轴表示对应步数下所有节点的免疫方差。由图3 和图4 可知，具有相似的节点对称性的相似性度量方法的曲线相近。因此，本文DDRE 方法验证了在SIR 模型下互为最相似的节点对的传播能力相似。

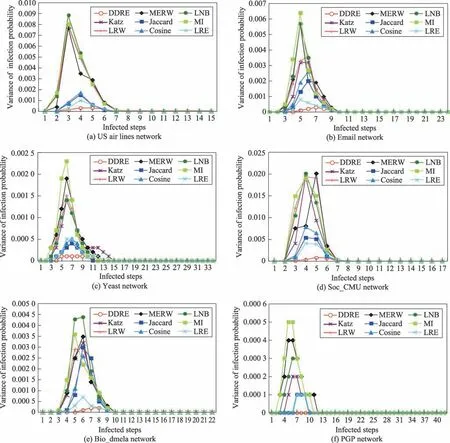
Fig.3 Variance of nodes’infection probability in different networks图3 不同网络中所有节点的感染方差

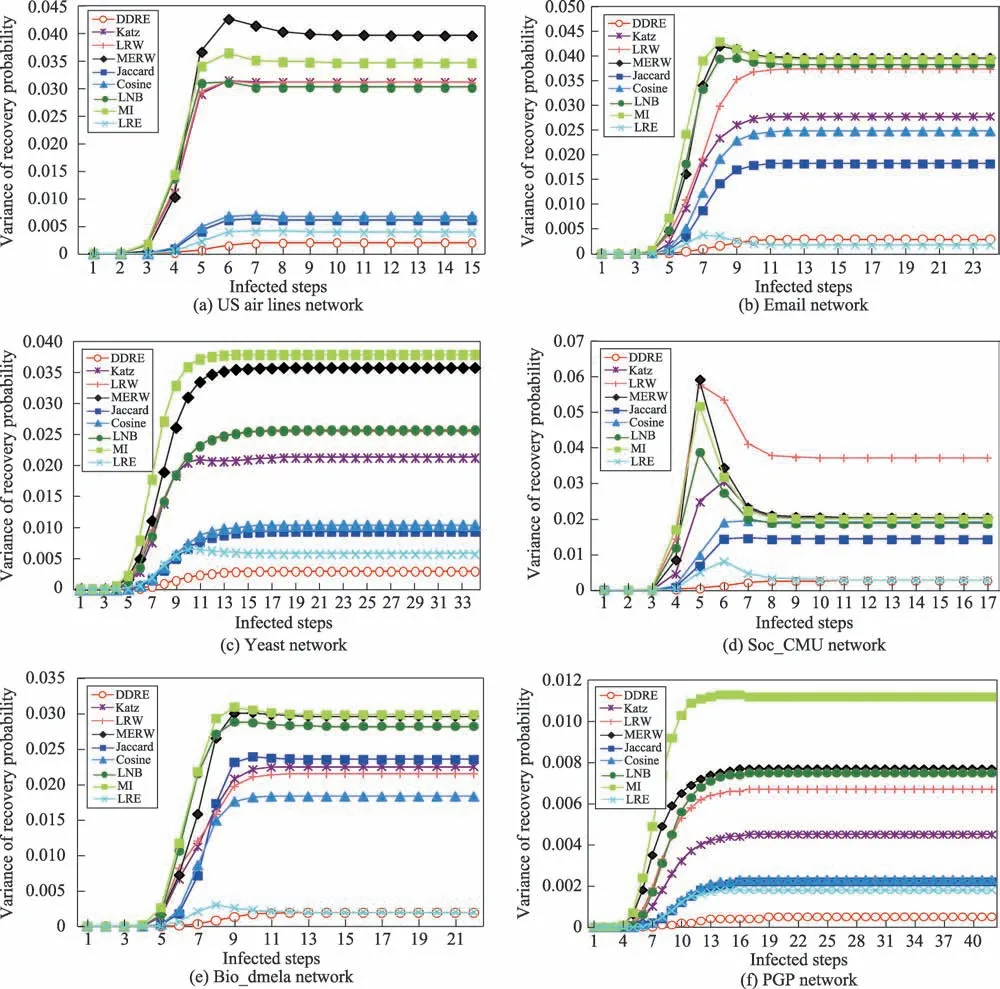
Fig.4 Variance of nodes’recovery probability in different networks图4 不同网络中所有节点的免疫方差

5 总结

本文提出了一种基于节点距离分布和相对熵的相似性度量指标DDRE。节点的距离分布以一种简洁的方式包含了详细的拓扑信息，且节点的距离分布可以刻画网络中局部结构的差异。通过生成节点的距离分布，利用相对熵度量节点之间的差异进而得到节点之间的相似性。通过与8 个相似性指标在6个真实网络上进行对比实验，结果表明DDRE 方法在对称性和SIR 模型中影响其他节点的能力方面表现出良好的性能。

度量复杂网络中节点之间的相似性是一项基础且具有挑战的工作。目前，节点的相似性广泛用于社区检测和链路预测，且相似性度量还有许多潜在的研究方向，如基于节点之间的相似性进行网络抽样，在抽样网络中比较复杂度较高的算法的性能。从节点相似性角度研究网络抽样可能会为人们提供新的角度去研究抽样算法。