融合节点标签与强弱关系的链路预测算法

王曙燕，巩婧怡

西安邮电大学 计算机学院，西安710121

链路预测通过已知的网络结构和节点信息等因素[1]，预测网络中两节点连接的可能性或发现已存在但未识别的隐式连边。在社交网络中，将用户视为节点，各用户社会关系视为连边，对可能存在关系的用户进行链路预测[2]。

常见的链路预测方法有：基于节点属性信息、基于网络结构和最大似然估计法[3]。然而，仅对网络节点属性的预测不能够真实精确地反映出目标网络的特性，并且与节点的属性信息相比，更容易获得网络的结构信息，而且网络的结构信息也相对比较可靠[4]。Liben-Nowell等[5]通过网络节点的拓扑结构相似性分析社交网络。后来出现的基于节点度的共同邻居CN（common neighbors）[6]根据节点的共同邻居进行推荐。王智强等[7]认为可借助链路预测检测由于信息或数据的噪声产生的不必要链接。

根据研究发现，仅考虑节点属性或网络拓扑结构的链路连接很难对节点信息进行较完全的刻画并不能更加精确地对节点进行链路预测。本文提出一种融合节点标签与强弱关系的链路预测（node labels and strong &weak relationships link prediction，NRLP）算法。该算法提取社交网络部分子图，通过对局部子图生成的目标矩阵进行分解，并将子网络结构融入节点标签、文本属性与关系强度的动态权重。该算法得到的节点向量兼顾网络结构属性、关系强弱与节点属性，且通过局部子图分析预测可能性比全图降低算法运行时间。

1 相关工作

链路预测是预测网络中的两个节点是否可能具有链路[8]。鉴于网络的普遍存在，它有许多应用，如朋友推荐[9-10]、知识图完成[11]和代谢网络重建[12]等。

一般来说，链路预测的研究可分为三大类：启发式方法、基于网络嵌入的方法和基于图神经网络的方法[4]。启发式方法[13-14]侧重于通过特定假设下节点之间的不同启发式节点相似性来估计连边的可能性。现有的启发式算法通常包括基于共同邻居CN 法[15]，当节点的共同邻居越多则对其连边，但此方法与现实生活情况不符。基于路径的算法：余弦相似性法[16]、Jaccard法[17]、基于路径的相似性法[18]（如Katz指标[19]、LHN-II指标[20]）等。基于共同邻居的的算法比较简单直观，但未挖掘网络所含有的丰富信息导致算法精确度受限，基于路径的算法虽考虑节点间的路径信息但计算复杂度较大。并且启发式方法对节点何时可能存在链接有很强的假设，当其假设在目标场景中不成立时，可能会失败[21]。

网络表示学习通过将节点表示为低维向量保留网络结构，然而在大型信息网络中该方法计算复杂、效率较低。随着skip-gram[22]算法出现的启发，DeepWalk[23]将基于随机游走产生的节点序列放入skip-gram模型输出表示。张学佩[24]定义了局部随机游走的节点相似度指标，并与其他相似性指标进行比较。结果表明，其提出的算法具有更低的计算复杂度。然而基于网络嵌入大多数算法具有很高的精度，但在学习节点表示时没有考虑到节点和边缘的丰富属性。

随着现有网络常用图表示，其中节点表示个体或群体，边表示个体或群体间的交互行为[25]，观察节点和边结构的内部特征，在保留复杂网络本身特征的同时，可以生成其独特的属性。为了提高预测性能，刘树新等[26]在网络拓扑特征中增加附加信息，但在提升性能的同时会增加计算复杂性。并且由于网络的复杂性，导致连接关系存在优劣性[27]，文献[28]提出可以用权重矩阵衡量关系的方法。

通过对现有研究成果的观察，时间效率和精确度都是链路预测中重要的因素。考虑现有研究在信息与属性方面的挖掘不足，本文采用双半径节点标签（double radius node label，DRNL）算法[29]，借鉴TELP 算法的思想，在分解目标网络的同时融入节点属性信息，并在其中考虑同一节点对于不同中心节点的关系强弱，赋予不同的动态权值，提出一种融合节点标签与强弱关系的链路预测NRLP 算法。其不仅通过局部子图可以更快速地挖掘网络所含节点位置信息，且在学习节点表示时考虑到节点和边缘的关系属性映射现实生活中的不同关系强度。最后，在三个数据上进行验证，并与常见链路预测算法进行对比，结果证明本文算法预测效果较好。

2 算法设计

对于网络图G=(V,E),其中，V为点集，E为边集，属性矩阵为T∈ft为属性特征的维度。由文献[30]的结果表明，局部子图保留了与链接相关的丰富信息，所以给定两个节点x,y∈V，生成(x,y)的h深度局部子图。

2.1 节点标签

为每个节点生成节点标签，表示为函数fl:V→N。对于在局部子图的每一个节点i，为其生成一个整数标签f(i)，在局部子图中使用不同的标签来标记中心节点与其他节点。通过节点表示差异性，在网络中准确找到目标节点并获得其相应结构信息[31]。

节点i在一个局部子图中的拓扑位置可以用它相对于两个中心节点的半径(d(i,x),d(i,y))表述。如果d(i,x)=d(j,x)并且d(i,y)=d(j,y)，则节点i和节点j在图中拥有相同标签。

首先，将中心节点标签设置为1。然后，对于(d(i,x),d(i,y))=(1,1)的任何节点，设置标签f(i)=2。半径为（1，2）或（2，1）的节点标签为3，以此类推。

两个中心节点，其中标签f(i)和双半径(d(i,x),d(i,y))满足：

（1）如果d(i,x)+d(i,y)≠d(j,x)+d(j,y)，则

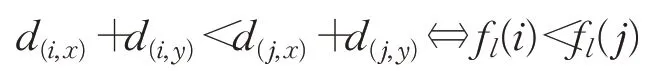
（2）如果d(i,x)+d(i,y)=d(j,x)+d(j,y)，则

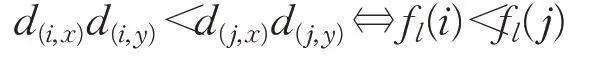
使用DRNL算法生成一个整数标签fl(i)函数，如公式（1）所示：

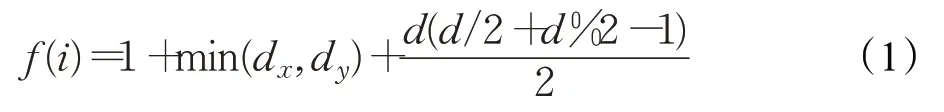
其中，dx=d(i,x)，dy=d(i,y)，d=dx-dy。对于d(i,x)=∞或d(i,y)=∞的节点，将其记做空标签0。

2.2 基于网络节点文本增强的链路预测算法

DeepWalk算法其实质为矩阵分解，因此，DeepWalk算法的目标函数为[4]：

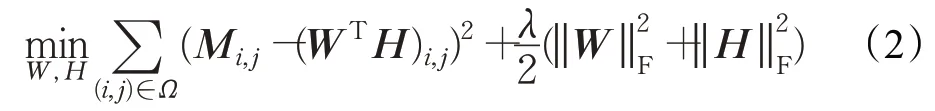
其中，W∈ℝ,H∈ℝ,Ω则为矩阵M的观测集，‖⋅‖F是矩阵M的F-范数，λ是平衡因子，它主要用来优化分解后的W和H矩阵，其原理等同于L2范数。

曹蓉等[4]提出了基于网络节点文本增强的链路预测算法TELP，在基于文本信息（text associated Deep-Walk，TADW）算法的基础上对目标矩阵M进行分解，并根据余弦相似性算法，计算出任意两个节点的相似度，从而构建出最终的相似度矩阵。

在目标矩阵M的分解过程中，使得下式达到最小：

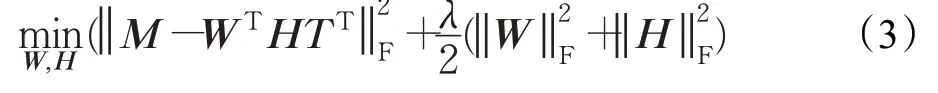
2.3 融合节点标签与强弱关系的链路预测算法

定义1（余弦相似度）图中任意两个节点的相似度可用余弦相似度表示为sim(x,y)=cos(x,y)+a，其中，x和y分别为目标节点和对比节点，a为调节参数，避免相似度过低导致的无效状态。

然而根据关系相关理论[32-33]，本文在余弦相似度计算公式的基础上根据关系强弱的特点，提出了一种融合节点标签与强弱关系的链路预测NRLP算法，其具体框架如图1所示。

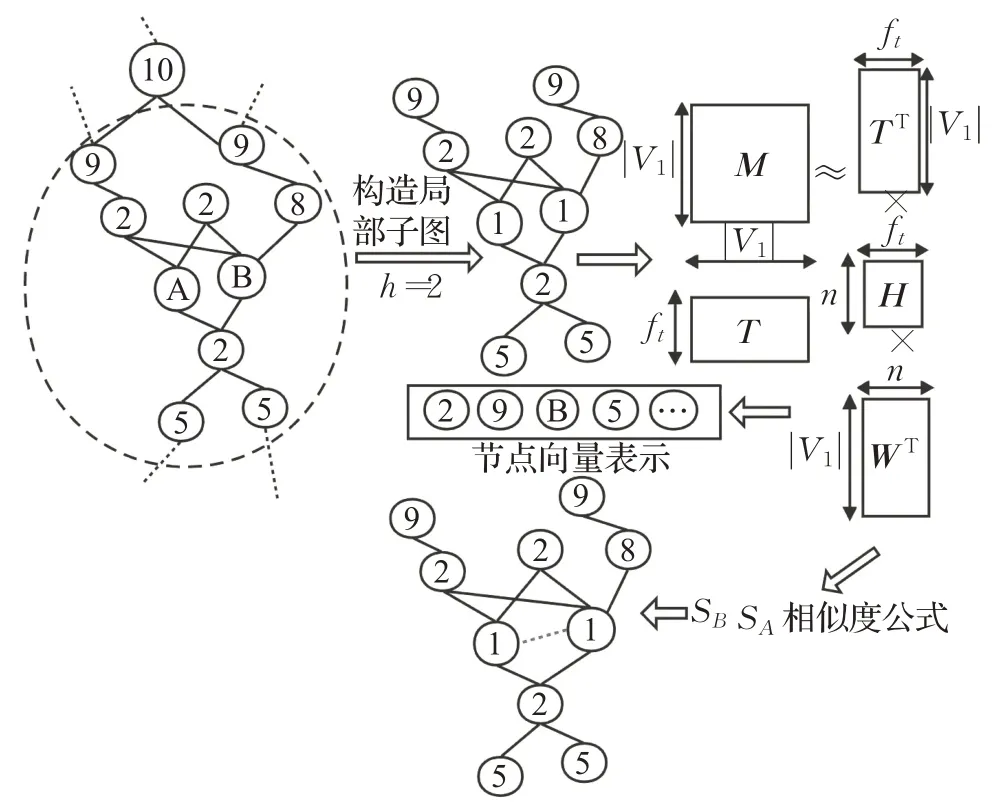
图1 融合节点标签的属性增强链路预测方法框架Fig.1 Attribute-enhanced link prediction method framework for fusion node labels

如图1所示，该方法在已有的关系网络中任意选择两个节点记为中心节点A、B，对关系网络使用DRNL算法生成节点i相对于中心节点A、B构建节点标签图G。其次基于γ衰减理论局部子图保存了丰富节点的信息，则以节点A、B 为中心构建深度为h的局部子图，提取局部子图中节点的特征矩阵M，基于式（2）对生成的特征矩阵M进行分解，并在矩阵分解过程中，引入属性特征矩阵T，对每个节点进行向量表示并使其融入节点属性因子，使分解后的矩阵、Hn×ft分别包含矩阵M、T的分解因子。其中，| |V1为h深度的局部子图中节点个数，n为向量长度。最后使用矩阵WT作为节点的向量表示，结合NRLP 算法，得到任意两个节点之间的相似度，对相似度高的中心节点进行连接，实现链路预测。

对所有分解得到的矩阵WT按比例分为训练集和测试集，并使用AUC评价指标，对本文算法性能进行评估。本算法的通过DRNL 算法计算节点标签其时间复杂度为O(|V|2)及TELP 模型学习节点向量表示其训练复杂度为O(|V|2)，但本文在节点表示向量的训练中才用局部子图进行训练，其复杂度明显小于原模型全图所有节点进行训练。所以本文提出的NRLP 算法时间复杂度为O(|V|2)。

NRLP 算法考虑节点之间存在强弱关系，赋予其不同的权重，表示节点i相对于两个中心节点x、y的不同关系程度。在局部子图中，当节点i的dx=1,dy=1,f(i)=2 时，则节点i对于中心节点x、y为强关系，反之则为弱关系。若节点i的中心节点的半径dx＜dy，则节点i相对于节点y与节点x有着更强的关系程度，反之亦然。而当dx=dy，则节点i与节点x、y有着相同的关系程度。由于节点i，对于不同中心节点生成的局部子图会拥有不同的强弱关系，所以对其赋予不同的动态权值，其计算表达式如下所示：

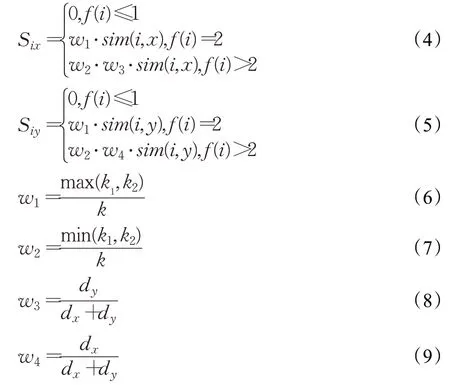
公式（4）～（9）参数含义如表1。

表1 NRLP算法参数说明Table 1 NRLP algorithm parameter description

对于节点标签为1的节点x、y，生成各自的相似度矩阵Sx=[Six]、Sy=[Siy]。构建Sx、Sy的相似度矩阵差S=Sx-Sy，在局部子图中，当除中心节点x、y以外的节点标签全为0时，则两个节点完全不相似，其|SST|=0也认定两节点不能连接。当其余节点标签不全为0，且|SST|<ε时，对节点x、y进行链路连接。其中ε为相似阈值，只有相似度小于阈值时，认为两个节点可能成为好友。

2.4 NRLP算法

NRLP算法描述如下：

3 实验结果与分析

3.1 数据集和实验设计

根据第2章所述一种融合节点标签与强弱关系的链路预测算法，对数据进行验证。实验环境为Windows 10系统、Intel Core i7 处理器、32 GB 内存，采用PyCharm开发环境，Python 3.6进行算法实现。采用三个常见的数据集Citeseer、DBLP和Cora数据集进行实验，验证本文提出的算法有效性。数据集包含了节点之间的连边关系和每个节点的属性类类别。数据集信息如表2所示。

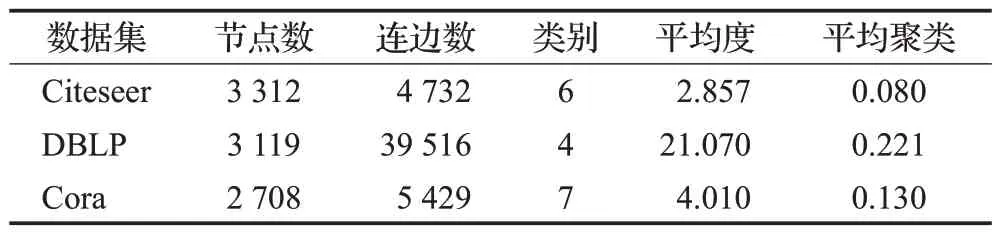
表2 数据集信息Table 2 Data set information

通过表2 可以看出，当节点个数大致相同时，边的个数影响了图的稠密度、平均度及平均聚类系数的大小。本文提出的NRLP 算法建模带有属性节点之间的关系，且对社会关系设置动态权重，得到的表示向量包含关系因子，结构因子及属性因子。

3.2 评价指标

常见的链路预算精确度衡量指标有AUC、准确率、排序分等。本文采用AUC 评价指标衡量算法的准确性。链路预测算法在经过训练后可以得到网络中每一对节点的相似值。AUC评价指标即是基于测试集中边的相似值和不存在的边的相似值的比较，如果测试集中边的相似值大于不存在边的相似值，则证明算法预测效果好。将数据集划分为测试集和训练集，其中90%作为训练集，10%作为测试集。从测试集中每次随机选一条存在的连边，再随机选一条不存在的连边。若存在的连边分值大于不存在的连边分值，则加1；相等则加0.5。通过n次独立比较，若有n′次大于的情况，n″次相等的情况，则AUC表示为：

AUC评价指标取值范围应为[0.5，1）。当训练集越大，对应的AUC值越高，则算法的精确度越高。

3.3 对比分析

为进一步验证本文提出的算法有效性，将本文算法与现有的多种预测方法进行对比。在实验中，对三个数据集设置训练比例为0.7、0.8、0.9，子图深度h为2，向量长度为200，相似阈值为0.000 16，实验链路预测结果如表3所示。

从表3 可以得出，将本文所提出的NRLP 算法与常见的链路预测方法比较，通过对比结果得出本文提出的NRLP 算法在三个数据集上的性能优于表3 中多种方法，并在Citeseer数据集性能最佳。由结果分析可知：本文所提出的NRLP算法优于目前大多数链路预测方法，其原因在于考虑节点的连接与属性信息；并考虑连接关系的强弱，区分其关系强度与程度生成新的相似度计算方法；并通过无监督学习训练节点表示向量，快速提取节点信息及其结构特征。

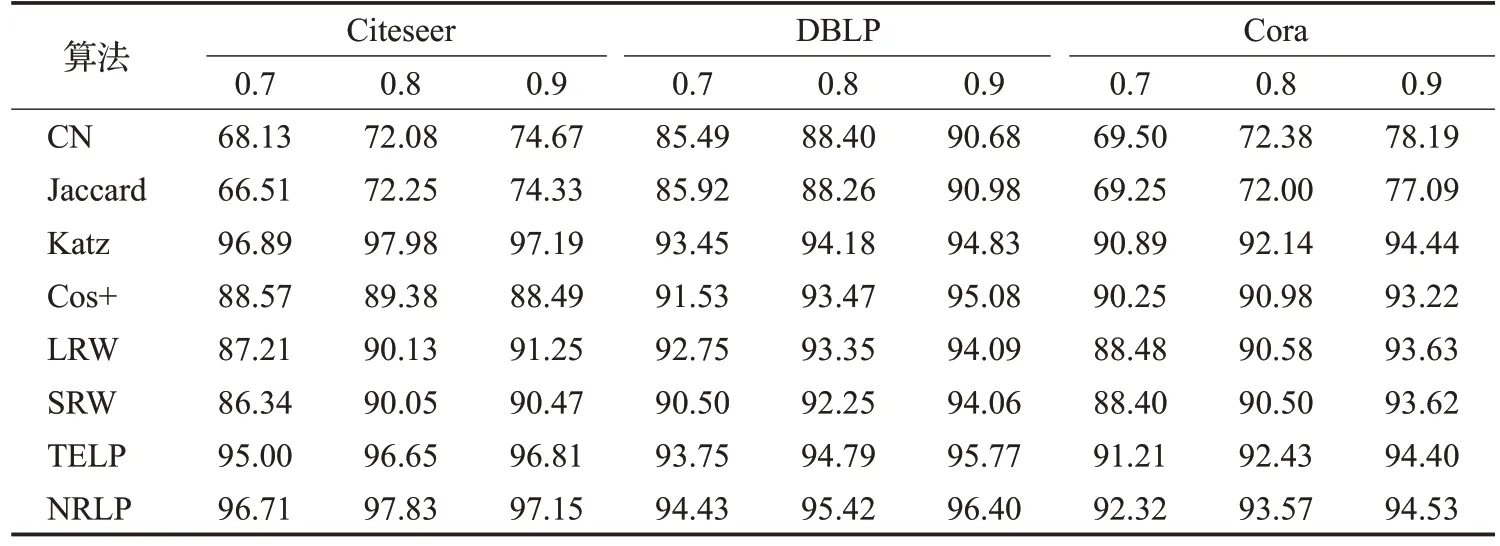
表3 数据集不同训练比例链路预测AUCTable 3 Link prediction AUC with different training ratios in data set %

3.4 调参与分析

在本文实验中，需要设置训练比例、向量长度n和局部子图深度h的值。通过调整局部子图的深度，获取两中心节点的不同邻居节点及其局部子图范围内的各节点属性，比较局部子图与原图之间的差异。

由图2 可知，本文对三个数据集在深度h为1～5 的局部子图性能进行评估，当h=2 时，均达到最佳性能。AUC 值在h>2 时减小，这表明子图越深可能会从远处节点引入噪声。当h=1 时，因为路径较短时，节点及属性信息较少导致差异较大。当长度变大时，引入路径信息减少局部子图与原图之间的差异。

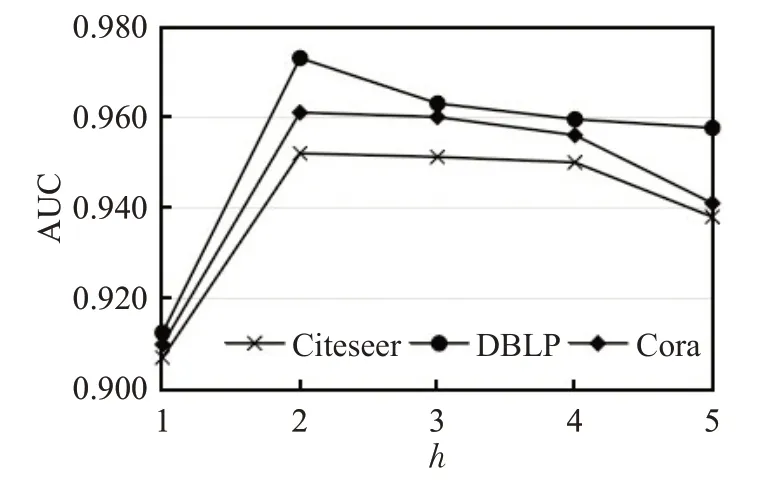
图2 局部子图与原图对比图Fig.2 Comparison of partial sub-image and original image

不同的训练比例与向量长度对精确度拥有不同的影响，当局部子图深度为2，相似阈值为0.000 16，得到的训练率及向量长度对预测结果如图3所示。

通过分析图3 可以得出，向量长度为50、100、150、200、300，训练集比例为0.70、0.75、0.80、0.85、0.90、0.95，Citeseer数据集和Cora数据集为较稀疏图。当向量长度分别为300、150，训练率分别为0.75、0.90 时，AUC 指标最优；DBLP 数据集为较稠密图，向量长度大于100，训练率在0.75～0.95之间，AUC幅度相差不大，基本在一定范围波动。对于稀疏图，向量长度与训练率对AUC 影响较大，对于稠密图，影响相对较小。

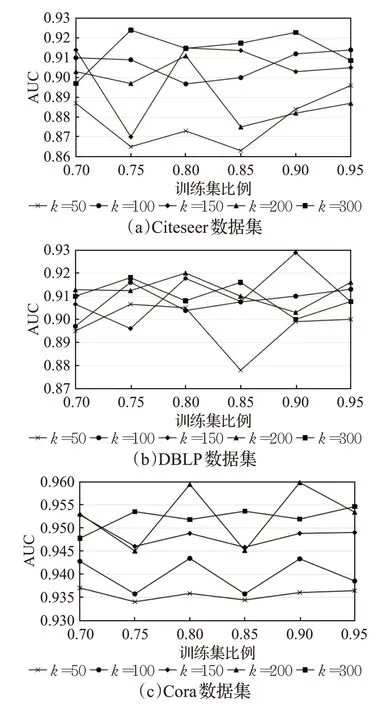
图3 训练率、向量长度与预测结果的关系Fig.3 Relationship between training rate，vector length and prediction result

为了证明NRLP 算法的效率，同时对比TELP 算法在原图和本文算法在局部子图上进行的时间见表4。

从表4 中可以看出，数据量较大时，在局部子图上算法效率更高，局部子图的噪音少于原图且表示向量更加高效，所以表现明显优势。

表4 算法运行时间对比Table 4 Comparison of algorithm running time s

4 结束语

本文通过对节点生成标签构造h深度子图在链路预测时提高算法运行时间与效率，并采用TELP模型为基础，分析不同关系强度对链路连接的重要性，并将余弦相似度算法与动态权重相融合，提出一种融合节点标签与强弱关系的链路预测NRLP 算法。该算法同时考虑网络结构、节点属性及连接关系强弱对链接的影响，通过随机选择两个中心节点判断其成功链接的可能性。实验结果通过在三种文献的集成数据库Citeseer、DBLP 和Cora 数据集验证NRLP 算法的准确性和高效性。下一步工作将考虑对新闻资讯相关性或社交网络人际关系预测实现链路预测，并尝试将模型拓展融合更丰富的属性进行教育资讯的社会化推荐。