变工况滚动轴承故障诊断方法综述

胡春生，李国利，赵 勇，成芳娟

宁夏大学 机械工程学院，银川750021

在现代化装备制造业中，旋转机械设备正朝向重载化、自动化、智能化的趋势不断发展，其结构更加精密，功能更加复杂，是现代装备不可或缺的重要组成部分[1-3]。滚动轴承常被用于支撑旋转体、减小摩擦以及保证回转精度等，是旋转机械传动装置最重要的部件之一。由于轴承长时间高速旋转，常常伴随着磨损、高温、重载等严苛的工作条件，因此故障频发。研究显示，轴承发生故障是很多重大安全事故的诱因，一旦轴承发生故障，轻则停机停产，重则造成人员伤亡，给生产生活带来巨大灾难[4]。因此，对轴承运行状态进行实时监测以及故障诊断具有重大安全意义。经过国内外科研人员近40年的研究，轴承故障检测与诊断技术发展了大量的有效方法，如温度、油屑分析、振动、声发射、静电、超声等[5]。由于振动数据便于分析并容易获得，因此绝大多数的研究都是通过分析振动信号来进行故障诊断。

当前传统恒定工况的轴承故障诊断方法主要分为两种，一种是以信号分析为主的传统故障诊断方式，如EMD[6]、集合经验模态分解（EEMD）[7]和奇异值分解（SVD）[8]等，该方法依靠人工提取特征值，因此该方法十分依赖专家经验；另一种为以数据驱动为主的机器学习方法，如RNN（包括LSTM和GRU）[9-10]、Logistic回归[11]、支持向量机（SVM）[12]、人工神经网络（ANN）[13]和CNN[14]等，该方法无需人工参与，可自动提取信号特征，且准确率大大提高，因此被广泛应用于故障诊断领域。

然而在实际工程中，轴承运行环境是变转速、变负载的。例如，汽车的车速和载重变化、风力发电机组风速风向的变化、生产线上产品需求的变化等因素都会导致其轴承运行工况的变化，变化的工况导致振动信号出现幅值变化、脉冲间隔变化、采样相位不恒定等问题，从而造成故障特征的动态变化，仅靠单一手段进行特征提取的传统方法无法解决变工况条件下数据分布的差异问题，给变工况条件下的故障诊断带来巨大挑战。当前解决变工况问题的方法主要有三种，分别是信号解调和信号处理、深度学习和迁移学习方法。本文回顾近五年变工况轴承故障诊断方法进展，简要地介绍了各类算法的原理，总结其适用场景及优势与不足，并对未来的研究方向做出展望，为后续研究指明方向。

1 信号解调与信号处理方法

当轴承处于健康的运行状态时，产生的振动信号具有平稳性与随机性，但是一旦轴承发生故障，将出现周期性的冲击特性与一定的非平稳性[15]。由于基于时域的均方根（RMS）、偏度或峰度等统计量会因速度变化而变化，因此以这些统计量作为特征的故障诊断方法是无效的，在频域上会引起频域模糊现象。解决以上问题的方法主要有阶次跟踪以及时频分析等方法。

1.1 阶次跟踪法

轴承振动信号一般通过在驱动端、风扇端安装加速度传感器，按照恒定的时间间隔测得，由于轴承转动速度不断发生变化，导致采集到的信号不再具有周期性与平稳性。阶次跟踪法是解决变速问题中应用广泛的故障诊断方法之一。与按照固定时间间隔采样方式不同，最初的阶次跟踪通过硬件对振动信号进行等角度重采样，因此也被称为硬件阶次跟踪（HOT）[16]，该方法采集速度块，可在线实现。然而，当轴承转速变化较快时，需不断动态调整采样频率及滤波器的截止频率，导致出现一定程度的采样延迟和误差，而且，该方法需要可调模拟滤波器和模数转化器等硬件支持，不仅增加了系统的复杂性及成本，同时限制了硬件阶次跟踪法的应用。

为解决硬件阶次跟踪的局限性，发展了计算阶次跟踪法[17]。该方法以固定时间间隔获取振动信号并实时获得转速信息，然后根据转速计脉冲计算出的旋转相位通过数值插值算法对振动信号重采样，从而将时域振动信号转化为角域振动信号。通过信号分析等手段，提取故障特征，用于滚动轴承故障诊断。针对变速引起的频域模糊现象，张亢等[18]使用阶次跟踪法（COT）将时域振动信号重采样为角域振动信号后，对角域信号进行局部均值分解（LMD）得到多个乘积函数分量，通过分析各个乘积函数分量的频谱判断轴承的故障类型和损伤程度。SPRO、SPRI 和SPRR 等频域特征仅在平稳运行条件下有效表征轴承缺陷，但是在变速条件下将会失效，Farhat等[19]基于计算阶次分析技术，更新了SPRO、SPRI和SPRR 三个频域特征，进而提取故障特征。杨武成[20]利用计算阶次分析法对振动信号角域重采样后，进一步利用Hilbert 包络解调把低频故障信号从高频载波信号中解调出来，进而提取故障特征。尹学慧[21]认为Hilbert变换在轴承转速波动较大的情况下并不适用，通过对实验数据进行Envelope 函数包络、Hilbert 变换包络、平方包络等包络计算发现，基于Envelope函数的包络能更有效地计算出变工况下故障信号的调制阶次。基于此，通过阶次跟踪技术与Envelope函数包络相结合，研究了轴承的故障机理和不同转速下轴承的阶次值，从而在变速条件下实现故障诊断。尽管计算阶次跟踪法摆脱了模拟滤波器等硬件的局限性，节约了成本以及系统复杂性，但是精度严重依赖于插值，并且需要转速计获取速度信息，导致该方法的应用受到了限制。

在轴承转速信息不可用时，发展了无转速计的阶次跟踪法[22]，其中通过时频分析获得转轴瞬时频率的方法应用最为广泛。Wang等[23]将振动信号经过短时傅里叶变换（STFT），使用基于幅度和的谱峰搜索算法从TFR中提取瞬时故障特征频率（IFCF），然后基于阶次跟踪思想，对瞬时故障特征频率（IFCF）进行重采样，从而将非平稳时域信号转换为平稳故障相位角度（FPA）域信号，最后将FPA 域信号转换为故障特征阶（FCO）域信号并识别故障类型。Huang等[24]认为基于瞬时故障特征频率（IFCF）在TFR具有最大幅值的假设在某些条件下并不成立，因此提出了一种可靠的基于快速路径优化的多重时频曲线提取算法，该算法直接从TFR中提取包括IFCF、谐波和ISRF在内的T-F曲线，利用平均曲线曲线比来描述提取曲线之间的关系，通过比较平均曲线比与故障特征系数来实现故障诊断。Zhu等[25]认为角域隐藏着周期特征，为此将短时傅里叶变换与谱相关分析结合，提出了一种基于Teager-Kaiser能量算子（TKEO）和角域快速谱相关（Fast-SC）的故障特征提取方法。Zhao等[26]提出了一种无键相阶次跟踪法，首先使用无转速阶次跟踪（TLOT）方法从时域信号中提取转速信息，利用包络阶次谱（EOS）在阶次域中恢复轴承特征频率。实验结果表明，通过结合TLOT 和EOS 的优点，该方法能够在变速条件下有效、准确地识别出不同的轴承故障。Urbanek等[27]提出基于相位解调原理和联合时频分析的两步法精确提取转速曲线并完成模拟振动信号和实测振动信号的分析。Feng 等[28]开发了一种基于谱峭度的联合时变幅频解调频谱以及改变故障特征频率提取的时频集中方法。

无转速计的阶次跟踪法完全摆脱了硬件的限制，在一定程度上成功解决了速度信息不可用的问题，但是大部分研究都是基于短时傅里叶变换来估计转速信息，然而，STFT是一种线性的固定分辨率的时频分析方法，同时受Heisenberg-Gabor 不等式的约束，而变工况条件下轴承振动信号具有强时变、强非线性等特点，因此短时傅里叶变换无法从非稳定信号中精确估计瞬时转频，致使基于无转速阶次跟踪法的故障诊断准确率低于基于硬件阶次跟踪法和计算阶次跟踪法。

1.2 时频分析

尽管阶次跟踪法在一定程度上解决了变转速问题，但是容易扰乱原始信号的脉冲响应，导致包络畸变等问题，因此不能很好保证采样后信号的稳态特征，国内外学者通过时频分析来解决上述问题。

1.2.1 小波变换

由于快速傅里叶变换的窗口大小固定，无法针对频率自适应。小波变换使用面积固定而形状可变的窗函数通过多辨率分析能很好地平衡时间分辨率和频率分辨率，其本质为通过小波基函数对信号进行滤波和加权，小波基的选择是影响小波分析效果的关键。

（1）连续小波变换（CWT）

连续小波变换的数学原理为将振动信号与系列复共轭小波的卷积运算来实现，其数学表达式为：

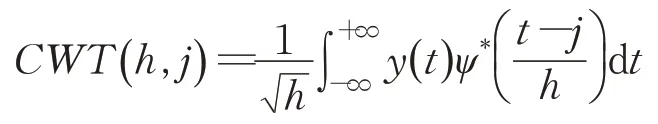
其中，ψ*表示小波基函数ψ的复共轭；h表示尺度参数或膨胀参数；j表示平移参数。

王晓龙等[29]为解决轴承失效早期，特征信号微弱，并且受传递路径衰减及环境噪声影响等问题，使用不同尺度的小波系数重构信号，从而得到不同尺寸的信号分量，依据峭度对信号分量进行合并，并利用相关分析进行特征筛选，保留峭度值最大的分量。杨蕊等[30]认为峭度忽略了信号的周期特性，因此使用相关峭度来分析信号在各个周期间的相关程度，从而确定最优小波尺度。陈科百[31]认为原始信号冲击成分能量决定连续小波分解系数的大小，信号与小波基越相似，分解出的系数值就越大，因此将信号进行连续小波变换后做小波尺度-能量谱图，并对小波尺度-能量谱图中的特殊尺度下的小波系数进行快速傅里叶变换，取得小波系数的频谱，最后通过分析小波系数的频谱从而提取特征频率。

小波分析是通过不同尺度伸展的柔性窗口和原信号进行对比获得小波系数，因而小波变换系数包含各种尺度下信号的信息，解决了傅里叶变换固定窗口的问题，因此可以处理突变和非稳定信号。然而在计算小波系数时，小波在每个时间尺度域上都是平滑移动的，因此连续小波变换具有较高的计算成本。

（2）离散小波变换（DWT）

对连续小波进行二阶离散化，将公式（1）中的伸缩因子“h”替换为“2j”，平移参数“j”变为“2jk”，就可以得到离散小波变换：

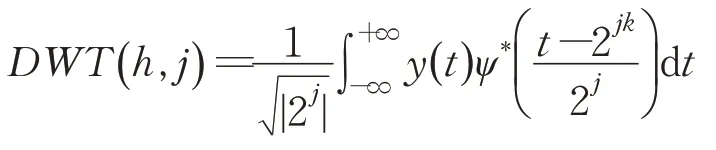
离散小波变换可以将信号分解为高频通道和低频通道，分解后的高频信号还可以继续被分为高高频和低高频，因此离散小波变换可以有效减少冗余特征。

Li等[32]将振动信号经过离散小波变换后，计算各尺度信号的方差，最后根据对数方差的斜率估计基于小波的多尺度斜率特征，实现了轴承缺陷的识别以及对齿轮磨损的诊断。

小波分析的最大特点就是所使用的小波基函数是通过小波函数经过平移、伸缩变换得到的，具有多分辨分析的功能[33]。通过这种多分辨率分析，在高频信号中获得一个好的时间分辨率和较差的频率分辨率，低频信号中获得较好的频率分辨率和较高的时间分辨率。尤其在故障诊断领域，故障信号是瞬态的、非平稳的，小波分析的局部化能力能最大限度去分析信号在时域和频域上的特征，从而准确刻画出信号在任意时刻的瞬时频率，这是傅里叶分析无法完成的。小波分析中不同的小波基函数，使其具有良好的多分辨率分析能力，能使时域分辨率和频域分辨率达到最佳平衡状态。而且，小波分析的时频分辨率可以根据信号自适应调整。对于信号中比较陡峭的成分，可在该区域使用高分辨率的小波来增加频率分辨能力，对于信号中平滑区域，小波分辨率可适当降低，从而达到时域频域分辨率的一个平衡状态[34]。小波1层分解后信号分为低频信号、高频信号两个部分，但是在2 层小波分解时，小波变换只对低频信号进行分解，高频信号不做变化，针对以上不足，国内外学者发展了小波包变换。

（3）小波包变换（WPT）

小波包变换是一种经典的多时间分辨率时频分析算法，信号经过小波包变换后得到低频带的近似系数和高频带的细节系数，弥补了小波分析只对低频成分进行分解的缺陷。信号经过小波包分解后，通过对分解后和滤波后的分量的动态特性进行统计学计算来实现故障的分类。信息熵、排列熵、模糊熵等动力学指标是使用的统计学方法。张雄等[35]通过计算样本小波包各子带的散布熵值来构建特征矩阵，通过主成分分析进行特征选择，较少冗余特征，最后采用Meanshift概率密度估计聚类中心位置。Rodriguez 等[36]认为扩展信息熵可以有效提高故障诊断准确率，因此提出一种平稳小波包结合色散熵和置换熵的故障诊断方法。

小波包分解的实质是对信号高频部分进行小波分解，因此从本质上来说两者只是在应用方面侧重点不同。轴承振动信号在转速比较高的情况下被载波调至高频，实验采集获得的信号中高频成分比较多，因此小波包分解比小波分解更适用于处理非平稳的振动信号[37-39]。波包分解对信号进行的分解更彻底，相比于小波分解更全面，对信号高频部分继续分解，使高频分辨率增加。

1.2.2 经验模态分解及其衍生算法

小波分析是通过不同尺度伸展的柔性窗口和原信号进行对比获得小波系数，因而小波变换系数包含各种尺度下信号的信息，解决了傅里叶变换固定窗口的问题，因此可以处理突变和非稳定信号[40]。然而在计算小波系数时，小波在每个时间尺度域上都是平滑移动的，因此连续小波变换具有较高的计算成本。在处理非平稳信号时，只要小波基选取得当，小波包分解就会具有强大的多分辨率分析能力，但是如何选取小波基成为限制小波包分解应用的重要因素，经验模态分解成功解决了该问题。

（1）经验模态分解（EMD）

经验模态分解将任意一个频率成分复杂的信号看做一系列本征模态分量的叠加，信号的频率信息、时域信息相互耦合，同时各本征模态函数相互独立，因此对非平稳信号进行经验模态分解实质上是一个解耦合的过程[41]。假设轴承故障信号为S(t)，其定义如下：

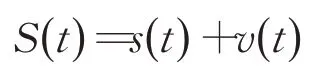
其中，s(t)为振动信号，v(t)为噪声。对用于含有噪声的故障信号进行经验模态分解步骤如下：

步骤1 确定故障信号S(t)的所有局部极值，应用样条插值法得到故障信号的上包络u(t)和下包络l(t)，通过下式计算上、下包络的均值m1(t)：

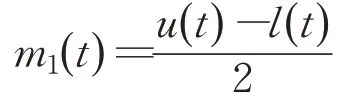
步骤2 故障信号S(t)与均值包络相减，即可得到第一个分量h1(t)：

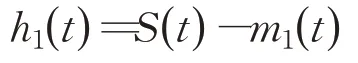
步骤3 若分解后的分量h1(t)局部极值点与过零点数量差不大于1，其极大值与极小值可构成包络线，且h1(t)的上包络线与下包络线均值为0，则h1(t)为本征模函数（IMF），若不符合，则重复步骤1与步骤2，符合上述条件后的h1(t)即为S(t)的第一个本征模函数（IMF）分量，记为c1(t)。分离后的信号如下式计算：

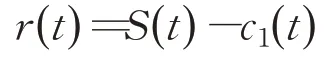
步骤4 将分离后的信号重新定义新的信号，并重复上述三个步骤，即可得到一系列本征模函数（IMF）分量ci(t)和残余分量。即原始信号S(t)为各本征模函数分量ci(t)与残差分量之和。

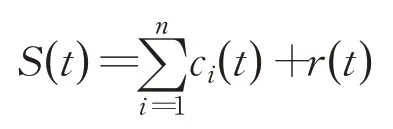
其中，r(t)被称作余项。

杨建华等[42]应用级联自适应分段线性随机共振系统对振动信号进行降噪，然后对降噪后的信号进行经验模态分解，从而提取故障特征。任学平等[43]将经验模态分解与AR谱相结合来提取故障特征，该方法将信号进行经验模态分解获得固有模态分量后，通过自回归模型进行特征提取，并由AR模型的参数和残差的方差组成了故障特征向量矩阵，最后进行分类。

经验模态分解无需借助小波基函数，只针对信号本身进行分解，消除了小波基的选取对信号分解的影响，并且分解后的本征模态分量都代表着原始信号的频率成分，残余分量rn(t) 代表了信号变化的平均趋势。然而，在对信号进行经验模态分解时，需确定信号的极值点，通过极值点拟合上、下包络线，并求得平均包络线，进而得到本征模态分量，由于噪声的存在，导致不同类别信号的极值点很容易发生变化，从而引起混叠效应，此外经验模态分解还存在边界效应、对噪声敏感等问题。

（2）集成经验模态分解（EEMD）

为了解决经验模态分解引起的混叠效应等缺陷，谷豪等[44]提出一种集合经验模态分解方法。该方法通过在分解的过程中加入具有零均值统计特性的高斯白噪声，以多次分解平均的方式来抵消信号的外来噪声，从而避免异常事件模式与固有模式的混淆，改善了经验模态分解的IMF分量的模态混淆现象，既保证了分解尺度分布的均匀性，又降低了异常事件的影响，凸显了振动信号的故障特征。王潇桐[45]通过对振动信号进行集成经验模态分解和模糊熵来进行特征提取，并以拼接的方式与时域特征进行特征融合，最后得到一个10 维故障特征作为支持向量机的输入，进而进行故障诊断。

时频分析方法通过提取轴承信号中的时频特征来进行故障诊断，因此信噪比越高，特征提取越容易。然而在故障发生早期，故障信号十分微弱，传统的时频分析方法很难从中提取特征，因此，国内外学者采用基于非线性系统的信号处理方法来解决上述问题。

1.3 基于非线性系统的信号处理

1.3.1 随机振动

1981 年，意大利学者Benzi 等[46]首次提出随机共振理论，用于研究古额尔德气象冰川变化，经过几十年的发展，现已广泛应用于机械故障诊断、物理以及数学等领域。与传统提出噪声方法不同的是，随机共振尽量保留原始信号，使噪声与原始信号产生共振，从而将噪声能量转移到微弱的信号中，从而完成微弱故障特征提取。传统的随机共振仅能对微弱信号(f<<1 Hz)进行特征提取，然而，当前旋转机械轴承发生故障时，其故障频率大约在几十到上千赫兹，某些高速列车的故障频率甚至达到几万赫兹，因此该方法失效。为解决上述问题，发展了几种微弱高频特征检测方法，如频率转移变尺度随机共振[47]、二次采样随机共振[48]、多尺度噪声调节随机共振[49]以及多尺度双稳阵列[50]等。影响随机共振的因素有三个，分别为周期性驱动力、噪声和随机共振系统，但是在实际应用中，噪声和信号本身往往无法控制，因此只能通过优化随机共振系统来产生最佳的随机共振。当前随机共振系统按稳态类型主要分为单稳态、双稳态与多稳态三种。

基于单稳态随机共振系统的非线性势函数，Zhang等[51]基于绝对势和指数势，构造了广义指数型单井势函数，然后数值分析了Levy 噪声驱动下相应的指数型单阱自旋共振系统的特性。针对采用粒子群算法调整单稳态随机共振系统的参数时，全局收敛时间较长问题，Liu等[52]提出了一种基于单稳态随机共振的粒子群优化算法，将线性惯性加权函数改为余弦函数的非线性函数，以缩短全局收敛时间。

基于双稳态随机共振系统的非线性势函数，田晶等[53]提出了基于容忍遗传算法（TAGA）的自适应双稳态随机共振（BSR）的中介轴承故障诊断方法，该方法在传统自适应遗传算法中引入容忍度思想，建立一种容忍遗传算法，采用容忍遗传算法对双稳态随机共振系统的结构参数a、b进行优化，建立自适应双稳态随机共振系统对故障信号进行处理。尹进田等[54]提出一种基于状态转移算法的参数同步优化随机共振新方法用于解决传统随机共振存在参数固定或仅对单个参数进行优化的不足问题。该方法采用移频变尺度方法将大参数信号变换成小参数信号，通过状态转移算法对随机共振系统的参数进行同步优化，以最大信噪比为优化目标，可同时获取系统最优参数，从而有效削弱信号中的噪声和增强微弱特征，从而实现早期故障准确诊断。以上方法在对双稳随机共振的系统参数进行调节时，会使势函数的势垒高度和势阱间距同时发生变化。为了能直观了解势函数特征的变化对双稳随机共振的影响，刘进军等[55]提出一种基于势函数特征参数调节的随机共振方法。该方法通过变量代换法实现势函数特征参数（势垒高度参数和势阱间距参数）的解耦，因此有利于势函数的调节。以上研究均基于对称势诱导随机共振的研究，但是在非对称势诱导随机共振中，阱深与阱宽非对称性同时变化，基于此，谯自健等[56]研究阱深和阱宽单一非对称双阱势诱导随机共振的微弱征兆特征增强机理，提出了非对称势诱导随机共振的机械重复瞬态特征提取方法。

基于多稳态随机共振系统的非线性势函数，马强等[57]通过对传统的双稳态随机共振进行研究改进，提出了一种三稳态随机共振，并对三稳态随机共振过阻尼布朗粒子的跃迁现象进行研究，分析不同参数下布朗粒子的函数变化，并采用变时间尺度方法对三稳态随机共振进行优化，在经傅里叶变换进行时频分析，由此提取出故障频率。张刚等[58]将混合双稳态随机共振系统与Woods-Saxon模型相结合，提出混合三稳态随机共振系统，然后利用自适应算法寻找混合型三稳随机共振系统最优参数组合，对α噪声背景下的仿真信号进行检测，证明其优越性。

上述研究均基于单个非线性系统，由非线性系统控制理论可知，多个系统协同作用有可能对系统的输出产生正向作用。王术光等[59]以级联随机共振为研究对象，采用人工鱼群算法对双稳态结构参数进行优化，进而设计随机共振系统，并利用该系统对滚动轴承故障信号的数据进行处理。Li等[60]提出双共振方法，在控制系统和被控系统中都输入周期信号和噪声，使得控制系统和被控系统均能产生随机共振，因二者之间相互作用，增强了被控系统的共振效应，实现微弱信号的增强输出。李伟等[61]将两个单一周期势系统线性耦合成一个新的系统，并采用粒子群优化算法自动匹配控制系统的相关参数，通过控制系统的输出反馈调节被控系统的随机共振，从而达到增强信号的目的。张刚等[62]通过将Duffing振子和Van der Pol 振子进行线性耦合，并将微分项作为耦合系统的反馈，从而增强耦合强度，形成一种Duffing与Van der Pol强耦合系统。为解决变换尺度的变化范围的选取缺乏固定标准、参数自适应效率低、检测到的目标信号不够明显等问题。张勇亮等[63]提出一种基于并联自适应随机共振的微弱信号检测方法。该方法综合考虑大参数信号发生随机共振时变换尺度与采样频率之间的关系确定基于采样频率的变换尺度的最大变化范围，通过尺度分段搜索、采用改进粒子群算法、共振系统并联等方法综合提高参数自适应的效率、突出检测到的目标信号，实现强噪声背景下微弱信号的快速、有效检测。

1.3.2 混沌理论

1963年，美国气象学家洛伦兹在研究天气预报模型时，发现用计算机求解一个确定的微分方程时，其解是非周期的且具有随机性，首次在一个确定性系统中从数值上得到混沌解，1975年，学者李天岩和约克首次将这种确定性方程产生随机现象命名为混沌[64]。近年来，发展了几种不同的混沌振子，在轴承故障诊断领域，Duffing振子是最常见的振子。

针对微弱信号特征提取困难问题，任学平等[65]改进了Duffing 振子的非线性项，成功将其应用于轴承故障诊断领域。李岭阳等[66]将混沌振子检测法应用于滚动轴承外圈、内圈和滚动体故障信号的检测中，通过输出相图的变化来判断故障信号是否存在，有效地实现了对滚动轴承故障信号的检测。刘彬等[67]分析了微弱周期信号相位角对检测系统的影响，提出采用多相位混沌振子阵列来消除微弱周期信号相位角对检测系统的影响。针对现有混沌振子难以检测频率未知微弱信号这一难点，李国正等[68]提出利用Duffing、振子输出值的方差峰值结合遗传算法检测淹没在强噪声背景中频率未知微弱信号的一种新方法，该方法采用具有相位偏移的Duffing振子阵列覆盖全相位，并结合遗传算法，优化求解不同频率输入信号下系统输出值方差的极值，以此得到待测信号频率的方法。以上方法只能同时检测某一频率的待测信号，黄继尧等[69]提出了一种可同时检测多个未知频率微弱信号的Duffing振子优化模型。该模型通过傅里叶与反傅里叶变换、频率截取和尺度变换后，得到相图在经过判决后输出结果。

1.4 本章小结

基于信号处理方法的关键在于人工提取特征的优劣，且严重依赖于插值以及信号分析处理的方法，通过对振动信号进行一系列的处理、变换和分析，将原始振动信号转化为时域信号、频域信号以及时频信号，再将这些人工提取的特征作为输入，使用隐形马尔可夫模型、支持向量机等机器学习方法进行故障分类。当前绝大部分的研究都是通过数值计算等手段，将高维数据特征转化为低维特征，从而减小计算量，并作为模型输入进行分类，因此该方法的分类性能严重依赖于人工特征值提取的好坏，且需要大量专家经验，导致完全基于信号分析处理的方法应用局限性较大，并逐渐被取代。随着深度学习的发展，国内外学者将深度学习应用到滚动轴承故障诊断领域。表1 总结了基于阶次跟踪和时频分析方法的优势、不足以及适用场景。

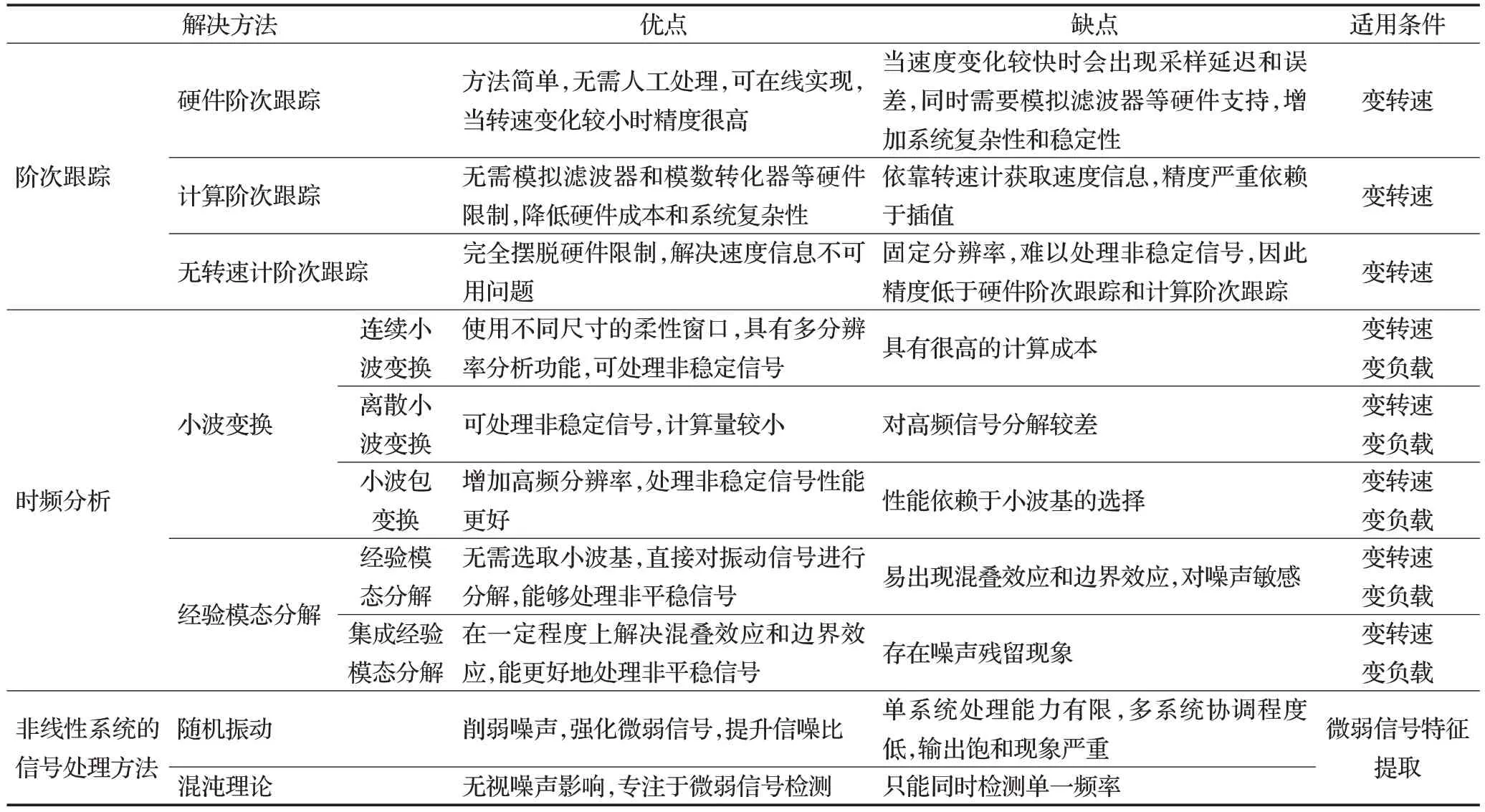
表1 基于阶次跟踪和时频分析方法Table 1 Order tracking and time-frequency based analysis methods

2 深度学习

神经网络省略了人工提取特征的繁琐步骤，无需专家经验，使用原始振动信号作为模型输入，即可完成故障诊断，是智能提取特征值的代表方法。但是在处理变工况轴承故障诊断问题时，由于传统神经网络的网络结构较为简单，网络层数较少，因此能够处理的非线性运算水平较低，仅能提取浅层特征，为解决上述问题，提出了深度学习概念。与传统神经网络不同的是，深度学习通常拥有更为复杂的结构以及更深的网络层数，底层特征逐层非线性映射到高维空间，特征表达随着网络层数的增加逐渐抽象化，最终形成层次化、抽象化的非线性特征[70]。并且网络层数越深，非线性拟合能力越强，能够处理的高维数据更加复杂。随着深度学习的高速发展，目前应用于变工况轴承故障诊断的神经网络主要有卷积神经网络（CNN）、深度置信网络（DBN）和自动编码器。

2.1 卷积神经网络

卷积神经网络于1994 首先被提出，是一种经典的分层神经网络[71]。因其权值共享等特点，致使其结构简单，特征提取能力强，因此在轴承故障诊断领域有非常广泛的应用。由于卷积神经网络具有分层的特点，且每层网络提取的输入为二维数据，其分层结构可以智能学习振动信号的故障特征，是一种高效的端到端的学习系统，Guo等[72]提出一种自适应学习率的分层卷积神经网络，第一层网络用于识别故障的类型，第二层网络用于识别故障的损伤程度，实验结果表明其变化的学习率可以有效提升模型的学习能力。Xia等[73]认为通过提取单一传感器数据的特征并不能有效减小不同工况下数据集的分布差异，因此提出一种多传感器的故障诊断方法。通过对从多个传感器测量的振动信号来提取不同工况下不变的故障特征，从而提升分类精度。张西宁等[74]认为传统的卷积神经网络在提取故障特征时，并不能只提取不同工况下的公共特征，因此提出一种小尺度卷积核以跳动的方式进行降采样的方法，试图通过改进传统卷积神经网络的模型结构来解决变工况问题。该方法使用滑动步长为2，激活函数为“relu”的卷积核代替传统的池化层。该方法不仅可以使输入数据的尺度降低一半，还可以在池化阶段进行特征提取，通过训练卷积核权重来选择有效的特征。赵小强等[75]使用三个3×3的卷积核以堆叠和串联的方式加入到残差块中，用于代替池化层，并将空洞卷积代替传统卷积层来扩大感受野，残差块以跳跃的方式连接不同层，以此来进行特征融合。Wu等[76]认为卷积核尺寸是影响卷积神经网络特征提取的关键，单一尺寸的卷积核无法同时平衡时间分辨率和频率分辨率，因此提出一种多尺度卷积神经网络来提取公共特征。以上方法都是通过人工调节参数的方法进行模型训练，Wang 等[77]将蚁群算法与卷积神经网络相结合，通过蚁群算法来优化卷积神经网络的超参数，从而避免了人工调参的弊端。Ince等[78]提出一个实时监控系统用于约束卷积神经网络中的权重，该方法不需要任何形式的预处理、特征转换以及特征提取，省略人工调参和特征提取的繁琐步骤，直接对原始振动信号进行评估。以上方法通过对原始振动信号进行特征提取进而进行故障诊断，而卷积神经网络在处理图像方面具有绝对的优势，因此潘成龙等[79]通过小波变换，将一维振动信号转化为二维时频图，以此进行故障诊断。陈里里等[80]将一维信号通过连续小波变换转化为二维时频图后，将三种故障特征图进行特征融合后输入到卷积神经网络中进行故障分类。张训杰等[81]将卷积神经网络与双向门控循环单元相结合，由卷积神经网络提取二维图像的空间特征，由双向门控循环单元提取时间特征，进而进行故障分类。

2.2 深度置信网络

深度置信网络兼顾生成模型和判别模型的优点，由可视层和隐藏层构成，是一种具有双层结构深层混合网络模型[82]。在轴承故障诊断领域，深度置信网络依靠无监督学习自动提取特征，将原始信号映射到特征空间，并依靠监督学习将特征空间转化为判别空间，从而进行故障类型判别，完成故障分类任务。

Tao等[83]最早将深度置信网络应用到滚动轴承故障诊断领域，通过构建编码器实现故障特征的提取，并将提取的低维故障特征作为模型输入，最后通过最小化输入输出的能量实现故障类别的判别。单外平等[84]认为尽管深度置信网络在提取故障特征时对输入数据进行了降维，但是计算量仍然十分巨大，因此在自动提取故障特征后，在训练判别器的过程中考虑了时间复杂度等因素，优先调节偏导数较大的参数，不仅提升了分类准确率，还大大降低了训练耗时。以上方法从原始振动信号中提取故障特征，在一定程度上实现了故障类型判别，但是当工况发生变化时，该方法准确率大大降低。王圣杰等[85]认为单一的振动信号不足以表征变工况条件下的非平稳信号，因此提出一种多传感器特征融合方法。该方法采用多个传感器在不同位置同时测得轴承振动信号，再对测得的信号进行特征提取。胡永涛[86]认为当工况发生变化时，深度置信网络自动提取的特征并不能解决训练集与测试集之间的分布差异，因此提出一种多特征融合模型。该方法首先对原始振动信号进行FCM聚类分析，从而判定该样本是否存在故障，并生成部分样本的故障标签，其次，分别提取振动信号的提取DTCWT 样本熵MMEMD 能量熵和VMD 样本熵，通过主成分分析方法，衡量三种特征的重要性，并给定一个权重，进而进行特征融合，得到一个同时包含三种特征的综合故障特征，最后将综合特征作为深度置信网络模型的输入，进行故障类型判别，实验结果验证了该方法的有效性。Chen 等[87]综合多传感器融合和多特征融合的优势，提出一种多特征融合及多传感器特征融合的DBN故障识别方法，准确率得到了进一步提升。Gan等[88]提出一种分层深度置信网络方法，该方法首先提取原始振动信号的小波包能量作为模型输入，第一层深度置信网络用于识别故障出现位置，同时第一层的输出作为第二层模型的输入，用于判定损伤程度，综合两层网络模型的结果，完成十分类任务。为了进一步提升模型分类准确率，深度置信网络与其他优化算法相结合的方法不断被提出。Liu等[89]将随机梯度下降算法应用到深度置信网络的训练过程中，同时，为避免某些模型超参数的设置影响模型分类性能，采用粒子群算法优化模型超参数，进一步提升模型准确率。熊景鸣等[90]将深度置信网络与支持向量机相结合，使用深度置信网络提取故障特征后送入支持向量机中进行分类，取得了良好的效果。Shao 等[91]认为尽管深度置信网络避免了人工提取特征等繁琐的步骤，但是这种方法提取的特征维度过高，导致计算量很大，因此将主成分分析应用到特征提取过程中，对高维特征进行特征选择后，降低了特征维度，在提升准确率的同时减小了训练耗时。

2.3 基于自编码器的轴承故障诊断

自动编码器是一个输入输出相同、具有自我学习能力的神经网络，由编码层和解码层组成。其中编码层由输入层和隐藏层构成，解码层由隐藏层和重构层组成。网络模型的编码过程就是将输入的高维特征经过激活函数的特征映射后，转化为隐藏层的低维特征，解码过程就是将隐藏层的低维特征经过激活函数重构为输出目标。自编码器的训练过程，就是通过构建不同的优化函数，实现目标输出与输入之间的损失值达到最小。Jia等[92]使用一个五层的自动编码器优先进行了故障的诊断。Yang等[93]使用将高斯核应用到深度自动编码器中，实现了故障分类。童靳于等[94]采用最大相关熵代替传统的均方误差作为损失函数，同时，为减小重构误差，加入了稀疏惩罚项和非负的约束因子收缩惩罚项，最后，通过灰狼优化算法对模型中的产参数进行优化，避免了人工调参等繁琐复杂的任务，从而实现变工况轴承故障诊断。

2.4 本章小结

深度学习方法侧重于挖掘数据层的规律，利用自身强大的特征提取能力，挖掘不同工况间相同的特征来解决变工况问题。该方法通过大量的数据训练模型权重，智能挖掘故障特征，避免了人工提取特征等繁琐的步骤，是实现变工况轴承故障诊断的有效方法。然而深度学习内部计算机制的可解释性很差，缺乏理论支撑，导致无法清楚诠释数据蕴含的领域知识[95]，并且当输入特征维度过高时，深度学习模型的模型计算成本巨大，导致需要花费大量的训练时间成本，并出现特征同质化等问题，因此限制了深度学习方法的应用，迁移学习方法成功解决了上述问题。表2 总结了各类深度学习方法的特点以及优缺点。

表2 深度学习方法Table 2 Deep learning methods

3 迁移学习

传统深度学习方法要求训练集和测试集必须独立同分布，当工况发生变化时，训练集与测试集会出现明显的域位移现象，因此限制了深度学习的发展。迁移学习可以在不同但相关联的两个领域内挖掘出公共特征。迁移学习已经成功应用于各个领域，在轴承故障诊断领域被广泛应用的方法主要有三种，即领域自适应、参数迁移以及特征迁移。

3.1 领域自适应

3.1.1 基于数据分布的领域自适应

基于数据分布的领域自适应假设数据的特征空间与类别空间均一致，而源域及目标域间的条件分布及边缘分布存在差异。通过减小域间的分布差异来解决变工况问题。根据数据分布，可分为边缘分布自适应、条件分布自适应和联合分布自适应三种。

边缘分布自适应是通过减小源域及目标域间的边缘概率分布距离来解决变工况问题，该方法最早由Sinno等[96]提出，并且通过MMD（maximum mean discrepancy）来计算域间分布距离。Chen等[97]基于迁移成分分析算法，提出一种变工况故障特征提取方法，在一定程度上解决了变域问题。Lu 等[98]提出一种具有领域自适应能力的深度网络模型，该网络模型采用自编码器来提取故障特征，使用MMD计算源域及目标域间的分布差异并作为优化目标。以上方法仅考虑了对齐全局域，而忽略了类内的相似性，忽略源域及目标域之间的关系会导致丢失每个类别的细粒度信息，条件分布自适应通过对抗的思想来对齐子领域分布，从而解决变工况问题。吴静然等[99]采用一维卷积神经网络进行特征提取，并且通过最小化局部最大平均差异和分类器损失函数，进行相关子域的分布对齐。在江南轴承数据集上验证了该方法的有效性。为了充分利用卷积神经网络强大的图像特征提取能力，董绍江等[100]采用连续小波变换，将一维轴承振动信号转化为二维特征时频图，采用完成预训练的Resnet-50网络结构来提取源域及目标域共同的特征，使用局部最大均值差异来度量子领域自适应，通过计算目标域伪标签以匹配条件分布距离来进行子领域自适应，从而减小域间的分布差异。Shen 等[101]认为边缘分布和条件分布对迁移学习的贡献不同，边缘分布对齐全局域，而条件分布对齐子领域，两种分布的相对重要性很难动态定量评估，因此单一使用某种分布无法满足要求，针对以上缺陷，提出一种动态联合分布对齐网络。该网络提出动态调整因子来定量比较MMD 和WCMMD 的相对重要性，从而同时对其条件分布和边缘分布，同时，为加权条件最大差异，财通软伪标签来代替模型输出的标签来改变条件分布的机算，从而有效减小条件分布的距离。以上方法在一定程度上解决了变工况条件下深层特征的域位移现象，但是杨春柳[102]认为网络较浅层仍然存在域位移现象，因此提出一种多层域自适应滚动轴承故障诊断方法，该方法将原始振动信号最为输入，使用一维卷积神经网络进行特征提取，并提出了多层域自适应和权重正则化项约束CNN 参数，从而减小因变工况而导致的特征分布差异。杨冰如等[103]采用预训练好的ResNet18 进行特征提取，并将不同残差块提取的深、浅层特征计算MK-MMD 距离，以匹配边缘分布差异，再将不同残差块提取的特征输入到分类器中输出伪标签，从而缩小条件分布差异。杨春柳[104]认为当样本数量过大时，使用MMD计算分布差异的成本巨大，而Wasserstein 距离几乎在任何位置都是可微的，因此选用Wasserstein距离来度量域差异，以此来减小计算成本。

3.1.2 基于数据选择的领域自适应

假设域间的类别空间一致，则认为域间的特征空间也一致。通过深度学习以及机器学习的手段，在不同域间提取相同的特征，以相同的特征作为模型的输入，从而实现变工况轴承故障诊断的方法称为基于特征选择的领域自适应。

基于特征选择的领域自适应的重点在于选择不同域间相同的特征，Long 等[105]认为在迁移学习中源域数据量大小并不是影响模型准确率的唯一因素，因此对源域进行样本选择，同时结合边缘条件自适应，从而达到变工况轴承故障诊断。Lu等[106]通过共享源域以及目标域特征的方法，实现无监督领域自适应，Tang等[107]提出一种EGR特征选择方法用于度量特征与类别间的非线性关系，从而解决变域问题，但是该方法为半监督学习，在迁移学习的过程中目标域仍然需要小部分带有标签的数据。但是带标签的跨域数据集很难获取，为解决该问题，郭亮等[108]提出一种跨数据集的变工况轴承故障诊断方法。该方法源域数据集为实验室条件下获取的带标签的数据集，采用带领域适配正则约束项的一维卷积神经网络进行特征知识的深度迁移适配，进而训练模型，最后将在实际工作环境中测得的数据作为目标域进行测试模型，实验结果验证了该方法的有效性。Yu等[109]提出一种保留局部流行结构的传递分量分析方法，该方法通过故障敏感性以及特征相关性进行特征选择，进而进行故障分类，通过两个不同测试平台收集的振动数据用于验证该方法，实验结果证明了该方法的可行性。

3.1.3 基于数据变换的领域自适应

基于特征变换的领域自适应的前提假设为源域及目标域在变换后的子空间中具有相似的分布，根据其变换的形式分为基于统计特征变换的统计特征对齐方法，以及基于流形变换的流形学习方法。

薛辉[110]将子空间分布对齐方法与概率分布自适应相结合，用于减小源域及目标域的分布差异，后又提出一种二阶特征对齐的方法，通过学习二阶特征变换矩阵，从而使源域以及目标域的欧氏距离最小。基于统计特征变换对齐方法可以在一定程度上解决域位移现象，但是基于统计特征的方法过于依赖专业经验，Zhang等[111]将故障特征嵌入到流行子空间进行特征变换后，再进行故障分类，从而减小域位移现象，刘海宁等[112]采用一维卷积神经网络进行特征提取后，将源域及目标域的边缘分布和条件分布进行对齐，从而进行变工况轴承故障诊断。以上方法虽然在一定程度上解决了特征发散问题，但是其只在子空间进行流形特征学习，并未在特征变换后的子空间进行分布对齐，并且进行子空间学习后，特征发散问题并没有完全消除，针对以上问题，王肖雨等[113]提出一种基于自适应噪声完整经验模态分解（CEEMDAN）与流形嵌入分布对齐的滚动轴承迁移故障诊断方法。该方法首先对原始振动信号进行自适应噪声的完整经验模态分解并进行特征选择，取其峭度最大的前6个干内禀模态分量作为故障特征，将故障特征嵌入流行空间进行特征变换，并将变换后的流行特征进行动态分布对齐，实验结果表明该方法可以有效解决特征发散问题。然而，童靳于等[114]认为以上方法仅仅通过最小化源域、目标域的分布差异来提升准确率，但是同一故障类别下样本间的分布距离同样影响迁移学习的效果，因此提出一种基于类内散度正则化的域自适应故障诊断方法，该方法将源域以及目标域嵌入流行子空间并动态对齐流行特征后，将类内散度引入到模型中，在减小源域以及目标域的分布差异后增大同一类别的聚集程度，使得模型分类准确率得到进一步提升。

3.2 参数迁移

参数迁移侧重于对离散模型权重的调整，即使用源域对模型进行预训练，再使用小部分带有标签的目标域数据集对模型参数进行微调，从而达到变工况条件下轴承的故障诊断。

Zhang 等[115]使用源域对模型进行训练后，冻结除softmax 外的层，并通过小部分带标签的目标域数据微调softmax层参数，从而达到变工况故障诊断问题，Shao等[116]采用与训练的CNN 网络模型代替随机初始化参数，仅改变最后全连接层节点的个数及权重来适应目标域的分类任务。Zhao等[117]认为不同尺度的卷积核可以提取不同的特征，在以往研究中特征提取的卷积核恒定，因此提出一种多尺度卷积神经网络迁移学习框架，使用MS1、MS2 以及MS3 三个尺度卷积核进行特征提取，再权重迁移的过程中，三个卷积和权重保持不变，只改变全连接层的权重，从而实现变工况轴承故障诊断。

由于权重迁移在源域对模型进行预训练后，需要部分有标记的目标域对模型权重进行微调，因此属于半监督迁移学习，当无法获得带有标签的目标域数据时，该方法将失效。

3.3 特征迁移

基于特征的迁移学习的主要任务在于寻找连接源域以及目标域的迁移函数来进行特征映射，通过学习特征映射来提取源域和目标域中可迁移的特征[118]。特征函数的作用是提取源域和目标域中不因转速负载等运行环境发生变化而变化的公共特征，从而实现变工况轴承故障诊断，因此，特征函数的选择是特征迁移的关键。

Wang等[119]提出一个可以将高维振动信号映射到低维潜在空间的主特征函数，在保持数据特征的同时有效减小了域位移，Han 等[120]结合神经网络与联合分布算法，提出一种具有搜索和标记功能的识别框架，该框架识别源域后，可以自适应目标域的条件分布，从而实现变工况故障诊断。Wen 等[121]提出一种三层稀疏自动编码器，并以最大均值差异作为损失值来提取源域和目标域公共的特征。

3.4 本章小结

迁移学习将变工况问题转化为域位移问题，通过特征提取、特征变换以及特征选择等手段，成功解决了变工况导致的数据分布差异问题[122]，在变工况轴承故障诊断领域取得了巨大的成功。然而，当前迁移学习仍然需要大量数据去训练模型，当工况差异较大并且含有噪声时，迁移学习的性能会显著下降。表3总结了迁移学习方法的特点以及优缺点

表3 迁移学习方法Table 3 Transfer learning methods

4 结论与展望

4.1 结论

随着社会的发展，旋转机械越来越智能化、信息化，对旋转机械的运行状态在线监测具有重要意义，在此背景下轴承故障诊断技术得到了长足的发展。目前变工况故障诊断领域主要发展了信号分析处理、深度学习和迁移学习三种方法，本文综述这些方法近五年的进展，主要得出以下四条结论：

（1）基于信号分析的阶次跟踪法将等时采样转化为等角度采样，以此解决变速问题，因此计算量很大，且严重依赖于插值精度。并且该方法仅能解决变转速问题，而无法解决变负载问题。

（2）基于信号分析的时频分析方法通过将始于信号转化为时频域信号，人工提取特征值，以此挖掘不同工况中不变的特征。特征值的提取直接影响着故障诊断效果，因此十分依赖专家经验，导致逐渐被取代。

（3）深度学习省略手动提取特征等繁琐的工作，依靠自身强大的学习能力自动提取故障特征，实现变工况轴承故障诊断。但是深度学习方法需要大量带标签的数据训练模型，数据量越大，模型分类性能越好。当不同工况间的差异较大或者工况过于复杂时，模型性能急剧下降。

（4）迁移学习方法不再受训练集和测试集具有相同分布的约束，能够在不同但是相关的两个领域间挖掘出公共特征，能在一定程度上加快训练过程并提高分类准确率，同时减少为测试集打标签等繁琐步骤，有效解决变工况问题。但是在实际工业现场环境中，由于外界的干扰等因素，故障诊断识别率均有不同程度的下降，实际工业场景下复杂工况以及实时数据在线诊断仍然还有很多问题需要研究和解决。

4.2 展望

尽管深度学习和迁移学习尽管在变工况轴承故障诊断领域取得了瞩目的进展，但是仍然有需要改进或优化的空间，后续工作应从以下几方面着手：

（1）多传感器特征融合

信号处理方法均通过分析单个传感器测得轴承振动信号来提取特征，因此存在诸多问题。采用多传感器在多测点采集轴承运行数据可获得更加丰富的信息，例如信号的物理属性、空间属性以及时间属性，从而增加故障诊断的准确率与鲁棒性，因此，基于多传感器特征融合技术是未来故障诊断领域的发展趋势。

（2）不均衡数据集

以上研究均基于均衡数据集的故障分类，但是在实际生产生活中，在绝大多数时间内轴承均处于正常运行状态，一旦轴承发生故障，机械设备将停机检修，导致可以获取大量正常数据，而有故障的数据十分稀缺。基于数据驱动的深度学习方法可以取得良好性能的前提是需要大量带标签的数据训练模型，直接将类别不均衡的样本使用深度学习模型训练时，会导致模型学习到的特征更加偏向于正常状态的特征，但很难学习到故障类别的特征，导致出现严重的过拟合现象，因此不均衡样本分类问题是未来的研究内容之一。

（3）多故障分类

目前几乎所有的研究都是针对轴承的单故障分类，然而在实际工程中，轴承发生故障时可能出现多故障共存的情况，因此，轴承多故障分类是一个值得研究的领域。

（4）数字孪生技术

当前轴承故障均为实验室环境下人工制造故障，因此不具备实际工程应用价值，而数字孪生技术在能源互联网行业、电力行业等均取得了初步成果。因此通过数字孪生技术采集真实场景下轴承运行数据，进而进行轴承运行状态监测及故障诊断是未来的发展趋势。