有限维Banach空间中完备集的构造
徐 珂,段博韬
(淮北师范大学 数学科学学院,安徽 淮北 235000)
0 引言
若n维欧氏空间Rn中一个内部非空的紧凸集,其任意一对平行的支撑超平面之间的欧氏距离均等于该集合的直径,则称该凸集为等宽集.显然,Rn中的球都是等宽集.此外,Rn中还有许多异于球的等宽集,关于Rn中等宽集的相关问题和结论详见文献[1-3].Rn中等宽集的概念可以通过不同的方式推广到一般的Banach空间中,其中常见的Banach空间中常宽集的定义方法如下[4]:设X*是Banach空间X的共轭空间,M是X中的一个有界闭凸集,集合δ(M)={‖x-y‖:x,y∈M}表示M的直径.若对任意的单位泛函f∈X*,有
sup{f(z)∶z∈M-M}=δ(M),
则称M是X中的一个等宽集.当X的维数有限时,有限维Banach空间中中心对称的等宽集只能是球;当X为无限维Banach空间时,该结论未必成立[5].
Banach空间完备集的概念最早是由Meissner在1911年研究Rn中的等宽集时给出[6]的(详见定义1).自此以后,有关完备集和其特征及性质的研究一直受到学者们的广泛关注[7-9].1958年,Eggleston 给出了在n维欧氏空间Rn中将集合完备化的方法,并且提到任何一个有界集都包含在一个与之直径相同的等宽体中[10].利用Eggleston构造法的思想,Papini和吴森林教授给出了在可分的Banach空间中将内部非空的有界闭凸集完备化的一种方法,但该方法需要无穷次迭代[4].
现有的一些完备集的构造方法通常都要利用过凸体直径的超平面,将凸体分割再进行完备化,其中Bavaud在文献[11]中研究得到了将欧氏平面R2中的集合完备化的一个方法:设M是欧氏平面R2的一个凸体,记凸体M的边界为∂M,如果任意选取两点x1,x2∈∂M,使得‖x1-x2‖=δ(M).此时,令H是一个过原点的超平面,H+和H-分别是由过点x1和x2的直线
Ma=(η(M)∩H+)∪(θ(M)∩H-),
Mb=(η(M)∩H-)∪(θ(M)∩H+),
式中:η(M)和θ(M)分别表示M的宽球包和紧球包(详见定义2),则Ma,Mb是M的两个完备化集.
2007年,Lachand-Robert和Oudet在文献[12]中也利用过凸体直径的超平面得到了将欧氏空间Rn中的集合完备化的一个方法.Papini和吴森林教授将Lachand-Robert和Oudet的构造方法进行了推广并证明了如下结论[4]:设H是Banach空间X中的一个过原点的超平面,H+和H-是由H确定的两个闭半平面,如果集合M满足条件
δ(η(M)∩H+)=δ(M)=δ(η(M)∩H-),
集合M1满足条件M⊆M1⊆η(M)-,则MC=η(M1)∪η(η(M1)+)-,并且MC是M和M1在X中的完备化集.
不难发现,Bavaud,Lachand-Robert和Oudet以及Papini和吴森林教授都是从低一维的完备集出发去构造高一维的完备集.本文将在文献[4]中构造法的基础上,用任意子空间替代超平面,把Papini和吴森林教授的构造法推广到高维的Banach空间中.
1 预备知识
设X是实Banach空间,用BX和o分别表示其单位球和原点.对于任意的x∈X,γ>0,BX(x,γ)=γBX+x表示以x为球心,γ为半径的单位球.若M是X中的任意一个有界集,则称
δ(M)=sup{‖x-y‖:x,y∈M}
为M的直径.符号intM,convM,∂M和clM分别表示M的内部、凸包、边界和闭包.对X中任意不同的两点x和y,用[x,y],[x,y〉和〈x,y〉分别表示点x和y之间的线段,以点x为端点且过y点的射线和过点x和y的直线.
定义1[4]设K是Banach空间X中的任意一个有界闭凸集,若对于任意的x∈XK,都有
δ(K∪{x})>δ(K),
则称K是一个(直径)完备集.
定义2[4]设K是Banach空间X中的任意一个有界闭凸集,若K0是X中的一个完备集,并且满足K⊆K0,δ(K)=δ(K0),则称K0是K的一个完备化集.
完备集的特征及性质通常借助于集合的宽球包和紧球包来进行研究.
定义3[4]设M是Banach空间X中的一个有界集,集合
称为M的宽球包.集合
称为M的紧球包.
由文献[13]可知,对任意a∈M,x∈η(M),有‖x-a‖≤δ(M).此外,η(M)还有另一种表述:
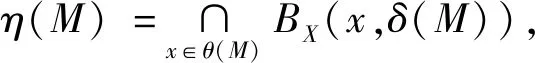
从而对任意x∈θ(M),y∈η(M),有‖x-y‖≤δ(M).
根据定义,η(M)和θ(M)有以下性质(详见文献[14-19]):
1)η(M),θ(M)都是凸体;
2)η(M)和θ(M)分别表示M的所有完备化集的并集和交集;
3)M⊆θ(M)⊆MC⊆η(M),其中MC为M的任一完备化集;
4)δ(M)=δ(θ(M))≤δ(η(M));
5)M是完备的当且仅当η(M)=M;
6)若M1⊆M2,并且δ(M1)=δ(M2),则η(M2)⊆η(M1),θ(M1)⊆θ(M2).
2 主要结果
本节将在文献[4]的基础上给出完备集的两种构造法,分别是对Bavaud构造法和Lachand-Robert及Oudet构造法的推广.
2.1 Bavaud构造法的推广
设X是n(n≥2)维的Banach空间,V是Banach空间X中的任意子空间,H是X中包含原点的一个超平面,且V⊂H.令K是子空间V中的一个集合.用H+,H-分别表示由H确定的闭半空间,令
η(K)+=η(K)∩H+,η(K)-=η(K)∩H-,
θ(K)+=θ(K)∩H+,θ(K)-=θ(K)∩H-,
并且
Ka=η(K)+∪θ(K)-,Kb=η(K)-∪θ(K)+.
显然,K⊆Ka∪Kb.
若K满足δ(η(K)+)=δ(K)=δ(η(K)-),则称K满足条件(dc).
定理1 设K是子空间V中的一个集合,H是Banach空间X中包含原点的一个超平面,且V⊂H.K0是一个不一定为凸的集合且满足K=K0∩H,δ(K)=δ(K0).如果K满足(dc),那么(K0)a和(K0)b不仅是K的完备化集,同时也是K0的完备化集.
证明这里只证(K0)a是K和K0的完备化集的情形,(K0)b的情形类似.由于K0⊂(K0)a,从而有δ(K0)≤δ((K0)a).故要证δ(K0)=δ((K0)a),只需要证明δ(K0)≥δ((K0)a).对任意的x,y∈(K0)a,若x,y∈η(K0)+,由于η(K0)⊆η(K),所以
‖x-y‖≤δ(η(K0)+)≤δ(η(K)+)=δ(K).
若x,y∈θ(K0)-,由事实θ(K0)⊆η(K0),有
‖x-y‖≤δ(θ(K0)-)≤δ(η(K0)-)≤δ(K).
若x,y由超平面H严格分隔开,不妨设x∈η(K0)+,y∈θ(K0)-,从而
‖x-y‖≤δ(K0)=δ(K),
因此,δ((K0)a)=δ(K0)=δ(K).
下证(K0)a是完备的.设z是X(K0)a中的一点,若z∉η(K0),则存在w∈K0,使得‖z-w‖>δ(K0),从而有
δ((K0)a∪{z})>δ(K0)=δ((K0)a).
假设z∈(X(K0)a)∩η(K0)=η(K0)-θ(K0)-,显然z∉θ(K0),那么存在w∈η(K0),使得‖z-w‖>δ(K0).又由于δ(η(K0)-)≤δ(η(K)-)=δ(K)=δ(K0),所以w∈η(K0)+.故
δ((K0)a∪{z})>δ(K0)=δ((K0)a).
从而,(K0)a是完备的.
综上,K⊆K0⊆(K0)a,δ(K)=δ(K0)=δ((K0)a)并且(K0)a是完备的,所以(K0)a是K的完备化集,同时也是K0的完备化集.同理可证(K0)b是K的完备化集,也是K0的完备化集.
2.2 Lachand-Robert和Oudet构造法的推广
Lachand-Robert和Oudet提出了一种更一般和更复杂的构造法,与Bavaud的想法有相似之处.本文将推广Lachand-Robert和Oudet的方法,即从低维的完备集出发去构造任意有限维的完备集.
设K是子空间V中的一个集合,H是包含原点的一个超平面,且K⊂V⊂H.K1是一个不一定为凸的集合且满足K⊂K1⊂η(K)-,令
K2∶=η(K1)+,K3∶=η(K2)-,KC∶=K2∪K3.
根据文献[4],显然有K1⊆K3.
定理2 设V是Banach空间X中的子空间,H是X中包含原点的一个超平面,设K⊂V⊂H.如果K满足
(dc):δ(η(K)+)=δ(K)=δ(η(K)-),
集合K1满足K⊂K1⊂η(K)-,那么,由
K2∶=η(K1)+,K3∶=η(K2)-,KC∶=K2∪K3,
可知KC不仅是K的完备化集,也是K1的完备化集.
证明由K⊂K1⊂η(K)-,有
δ(K)≤δ(K1)≤δ(η(K)-)=δ(K),
即δ(K)=δ(K1),从而η(K1)⊂η(K).又
K=K∩H+⊆K1∩H+⊆η(K1)∩H+=
η(K1)+=K2,
有
δ(K)≤δ(K2)=δ(η(K1)+)≤
δ(η(K)+)=δ(K),
即δ(K)=δ(K2),从而η(K2)⊂η(K).而K⊆K2⊆η(K2)意味着
K=K∩H-⊆K2∩H-⊆η(K2)∩H-=
η(K2)-=K3,
所以,δ(K)≤δ(K3)=δ(η(K2)-)≤δ(η(K)-)=δ(K),即δ(K)=δ(K3).因此,
δ(K)=δ(K1)=δ(K2)=δ(K3).
由于K⊆K2且K⊆K3,所以K⊆K2∪K3=KC,从而δ(K)≤δ(KC).故要证δ(K)=δ(KC),只需证δ(KC)≤δ(K).对任意的x,y∈KC,若x,y∈K2或x,y∈K3,此时‖x-y‖≤δ(K).不失一般性,不妨假设x∈K2,y∈K3,那么y∈η(K2),从而‖x-y‖≤δ(K2)=δ(K).
下证KC是完备的.设c∉KC.若c∈H-,那么c∉η(K2),因此,存在点y∈K2,使得‖c-y‖>δ(K2)=δ(K).若c∈H+H,那么c∉η(K1).而η(K3)⊆η(K1)意味c∉η(K3),因此,存在点z∈K3,使得‖c-z‖>δ(K3)=δ(K).这就得到了δ(KC∪{c})>δ(K),从而说明了KC是完备的.
综上,K⊆K1⊆K3⊆KC,δ(K)=δ(K1)=δ(KC)并且KC是完备的,因此,KC不仅是K的完备化集,也是K1的完备化集.
事实上,如果K⊂V⊂H且K满足条件(dc),则K的所有完备化集都可以根据Lachand-Robert和Oudet的构造法得到.
定理3 设V是Banach空间X中的子空间,H是X中包含原点的一个超平面,K是子空间V中的一个集合,即K⊂V⊂H.如果K满足
(dc):δ(η(K)+)=δ(K)=δ(η(K)-),
那么,K的所有完备化集都可以由定理2的方法得到.
证明假设C是K的一个完备化集,由定义有K⊆C,δ(K)=δ(C)并且C是完备的.那么C=η(C)⊆η(K).令K1=C∩H-,则
K=K∩H-⊆C∩H-=K1⊆η(C)∩H-=
η(C)-⊆η(K)-,
即δ(K)≤δ(K1)≤δ(η(K)-)=δ(K),从而δ(K1)=δ(K)=δ(C).
设K1,K2是由构造法K2∶=η(K1)+,K3∶=η(K2)-,KC∶=K2∪K3得到的集合.由K1⊆C有η(C)⊆η(K1).因此,
C∩H+=η(C)∩H+⊆η(K1)∩H+=K2,
从而C=(C∩H+)∪(C∩H-)⊆K2∪K3.又C和K2∪K3都是完备的,故C=K2∪K3.

