基于数值仿真的膨胀式压溃管阻抗性能研究

刘晓兵，周卫兵，戴如勇，潘勤涛，蒋宇锋

(1.中车戚墅堰机车车辆工艺研究所有限公司，江苏 常州 213000；2.常州中车铁马科技实业有限公司，江苏 常州 213000)

0 引 言

轨道交通中应用的吸能装置可在碰撞瞬间吸收能量、缓和冲击，是列车被动防护所采用的主要部件[1].列车车辆的钩缓装置是保证车辆编组和车辆连挂的重要部件，它是一种非线性吸能装置[2]，其能量配置是保证列车正常运行的重要参数.轨道交通车辆专用吸能装置主要通过金属材料塑性变形、压溃过程及综合过程等三种方式吸能[3-4].膨胀式压溃管作为典型的材料塑性变形的缓冲吸能保护装置而被广泛应用于轨道交通，其吸能变形过程是一个非常复杂的大变形过程，且该变形过程是不可逆的破坏过程，需要研究各项参数对压溃管阻抗性能的影响，但采用实物研究代价较高，因此，有限元仿真成为该研究的关键支撑技术.对于膨胀式压溃管的性能研究主要集中在数值仿真研究方面[5-10]，而对于实物试制和试验的研究鲜有报道.国内研究主要集中在碰撞时整体车辆的吸能分析，而对车钩缓冲装置的吸能分析较少[11-15].本文对压溃管进行建模，并对撞击与静压吸能阻抗力开展数值仿真和试验的对比研究，证明仿真方法的有效性及仿真与试验的差异点，还详细分析了压溃管产品的结构参数对其阻抗力的影响.

1 模型的建立

有限元仿真技术算法主要有三种：拉格朗日算法、欧拉算法和ALE自适应算法.本文以拉格朗日算法为主，同时兼有欧拉算法以及拉格朗日算法和欧拉算法相结合的ALE自适应算法.ALE自适应算法可以根据材料的变形自动控制材料内部发生自适应流动，并会根据变形进行自适应重划分，即变形严重、应力集中的地方，其网格划分更细，零件变形较小且应力分布相对分散的地方，其网格会自动划分较疏，这种算法结合拉格朗日算法和欧拉算法的优点，能够提高算法的响应速度和计算精度.

1.1 模型边界条件

1)控制方程设置：碰撞过程中，整体结构需满足动量守恒定律、能量守恒方程和质量守恒方程.

2)边界条件设置：压溃装置碰撞模拟仿真过程中，主要设置三种边界条件，包括位移边界条件(设置拉伸管的运动位移)、接触边界条件(设置压溃装置的自由度和接触算法)和面力边界条件(设置压溃管和拉伸管受到的力载荷条件).

1.2 模型的建立

压溃式吸能结构主要由拉伸管和压溃管组成，两管均为筒状结构，因此，将其简化为薄壁圆筒结构，利用三维绘图软件绘制拉伸管和和压溃管，将其导入，生成仿真模型.

对导入的拉伸管和压溃管进行网格结构设置，网格划分的稀疏直接关系到仿真的结果，划分过疏会导致仿真结果的可信度下降，划分过密会导致计算时间过长，甚至可能会由于网格变形发生中断.因此，经过多次模拟仿真之后，根据碰撞模拟仿真的特点，其网格划分采用如图1 所示形式，采用如下几个原则：1)模型网格中三角形单元不能超过10%；2)模型网格划分中，翘曲单元不能超过总数的15%；3)在碰撞能量的吸收区域尽量采用规则的网格划分单元，同时在非碰撞区域常采用较大的网格单元.

图1 膨胀式压溃管等效有限元模型示意图Fig.1 Schematic diagram of equivalentfinite element model of expandable crushing pipe

1.3 模型结构参数

压溃管装置整体结构简化模型如图2 所示，主要结构参数如下：D1为拉伸管的直径；D2为压溃管的直径；b为压溃管的壁厚；α为诱导锥面角.

图2 压溃管主要结构参数示意图Fig.2 Schematic diagram of main structural parameters of expandable crushing pipe

1.4 模型材料性能

模型材料选择某特定钢材，模型单元的机械性能属性采用表1 所示的参数，也即模型性能设计要求，其材料本构模型建立在式(1)的基础上.

表1 材料性能Tab.1 Material properties

(1)

拉伸管作为动力源，会在其碰撞方向上获得速度，压溃管在碰撞方向的自由度为零.在模拟碰撞仿真时，拉伸管通过刚性墙撞击，得到速度v=3.4 m/s，其总能量约为170 kJ，根据这些条件来分析拉伸管与压溃管之间的碰撞性能.

2 仿真与实物试验对比

本文压溃式吸能结构用于列车保护装置中，该装置能在列车发生碰撞过程中实现吸能，保护乘客生命财产安全.列车首节车厢的碰撞基本属于动态碰撞，而后续车厢编组的碰撞属于准静态碰撞，其变形原理可以等效为静压吸能.本文对撞击与静压吸能阻抗力同时进行了数值仿真和试验研究，其阻抗力对比曲线如图3(b)所示.由图3(b)可以得到如下结论：

(a)静压试验过程图

1)静压试验稳态阻抗力值与数值仿真稳态阻抗力值基本一致，差异小于5%，因此，本文数值仿真方法所得结果与实际基本相吻合，该数值仿真方法适用于压溃管等类型的膨胀式压溃吸能机构的设计开发.

2)数值仿真与静压试验的初始触发峰值即阻抗力峰值相差较大，其原因在于静压试验和冲击试验在初始触发状态存在较大的差别.目前，压溃管的主要考核指标仍为稳定阻抗力，但随着技术进步正在逐步开始研究冲击状态下，压溃管阻抗力峰值对冲击吸能过程的影响.

3)数值仿真和静压试验的稳态阻抗力值较为接近，但两者的波动振幅存在一定差异，即静压试验结果振幅波动较大，而数值仿真波动振幅较小，其原因是数值仿真中压溃管材料性能完全一致性，而实际中压溃管局部材料的性能仍存在一定差异.

综上所述，数值仿真结果和静压试验结果的偏差率远远小于10%，本文采用的数值仿真计算方法是可信的，可用于指导实际设计.

3 膨胀式压溃管性能的影响因素分析

为了更加贴合生产实际，根据实际压溃管装置的机械生产特性，预先选定的材料屏蔽了实际生产中无法直接检测或不易控制的因素(如材料性能、扩径比等).本文采用了诱导锥面角、壁厚和直径等便于实际生产控制的参数，并采用控制变量原则来研究各参数对压溃管性能的影响.

3.1 诱导锥面角对阻抗力的影响

根据单一变量原则，对15°，30°和45°三种不同诱导锥面角度结构的模型进行分析，所得曲线如图4 所示.

(a)压溃管阻抗力随时间变化的曲线

由图4(a)中可以看出：由碰撞开始时，阻抗力变化幅度较大，一段时间后，阻抗力开始趋于稳定，直到完全停止后，阻抗力完全消失；同时，诱导锥角越大，阻抗力也相应较大.

表2 列出了压溃管在不同锥面角下的阻抗力值，其变化趋势如图4(b)所示.由图4(b)可以看出：阻抗力初始峰值及其均值均随诱导锥面角度的增大而增大，在15°～45°的范围内，两者之间呈近似线性关系，拟合线性斜率为10.5；阻抗力与锥面角之间呈凹形关系曲线.因此，锥角角度必须控制在一定范围，过大时会引起膨胀式压溃管的不稳定变形，而过小时又会使压溃管总容量过小，不经济.

表2 不同诱导锥面角的压溃管阻抗力对比Tab.2 Comparison on the resistance of expandable crushing pipe at different induced cone angle

3.2 压溃管壁厚对阻抗力的影响

根据单一变量原则，对 5.5 mm，6.5 mm，7.5 mm，8.5 mm和9.5 mm五种不同壁厚结构的模型进行分析，所得曲线如图5 所示.

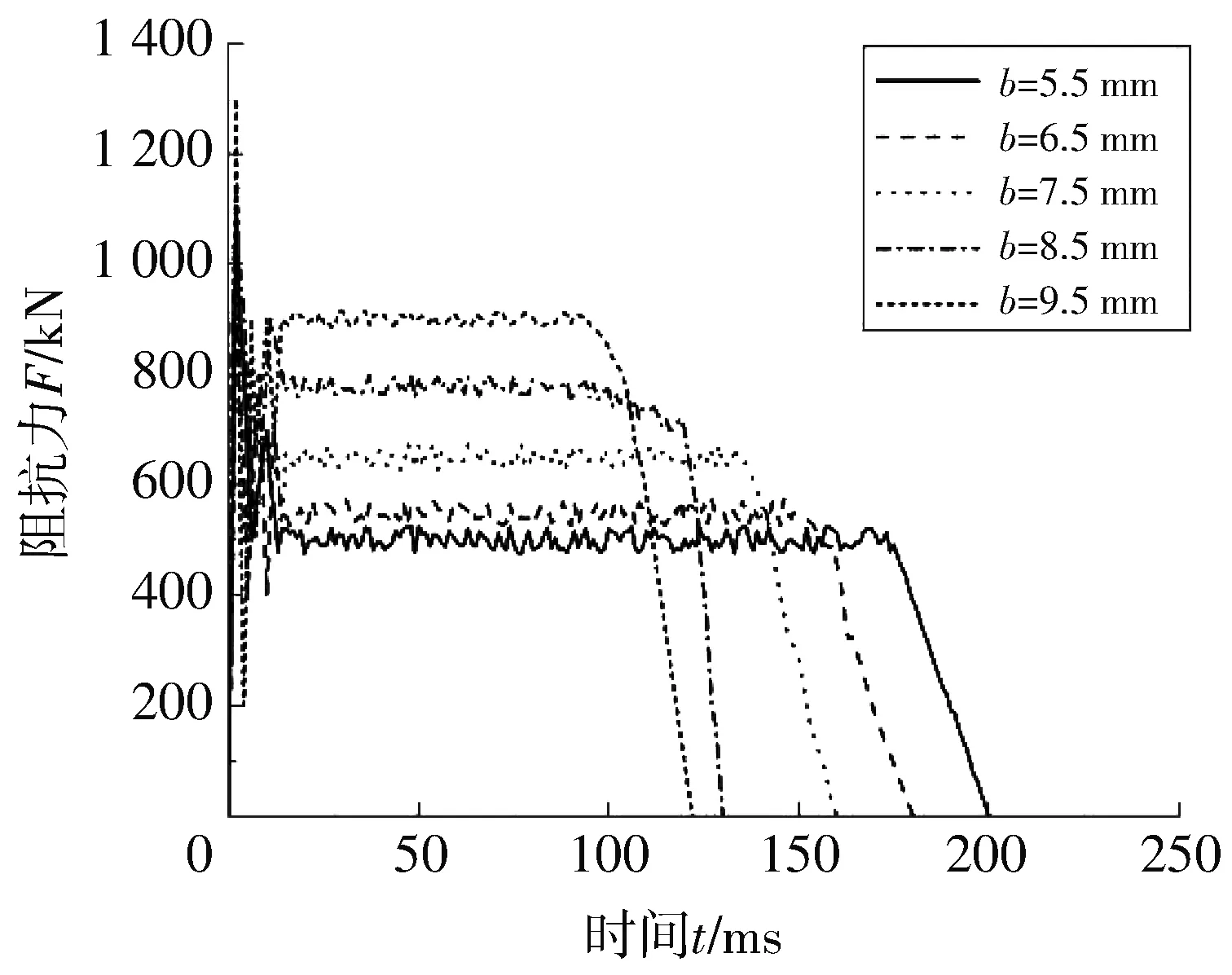
(a)压溃管阻抗力随时间变化的曲线

由图5(a)可知：压溃管壁厚由5.5 mm增加到9.5 mm的过程中，压溃装置的阻抗力不断增大，增大幅度均匀；同时，阻抗力波动幅度较大，这是由于材料变形不均匀，变形弹力不恒定导致的.

表3 列出了压溃管在不同壁厚下的阻抗力值，其变化趋势如图5(b)所示.由图5(b)可以看出：碰撞发生时，压溃装置的阻抗力与其壁厚相关性较大，随着壁厚的增加，压溃管的阻抗力明显增大，拟合线性斜率为82；壁厚的影响远大于诱导锥面角变化对阻抗力的影响.由表3 可知，不同壁厚的峰均比基本相近，且在1.58附近小幅波动，因此，可以认为阻抗力峰值和均值增加的幅度基本相同.因此，压溃管壁厚不能过大或者过小，例如，压溃管壁厚在5.5 mm时，其阻抗力均值为540 kN，明显较小，当相同的碰撞能量传递到压溃管时，其拉伸管运动有效行程必然增大，相应压溃管的变形长度增加，这必然增加了其在纵向的长度.

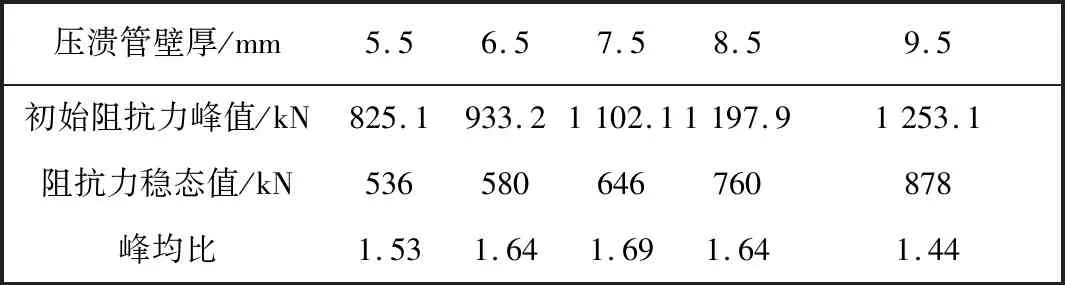
表3 不同壁厚的压溃管阻抗力对比Tab.3 Comparison on the resistance of expandable crushing pipe at different wall thickness

3.3 压溃管直径对阻抗力的影响

根据单一变量原则，对124 mm，134 mm，144 mm，154 mm和164 mm五种不同直径的模型进行分析.仿真结果如图6(a)所示.由图6(a)可以看出，能量吸收变化情况和压溃行程变化情况类似，当压溃管直径发生变化时，压溃管阻抗力变化并不显著，且各个直径下阻抗力波动的规律和幅度基本相同.

(a)压溃管阻抗力随时间变化的曲线

表4 和图6(b)表示不同直径下模型阻抗力的变化情况.由图表可知：随着压溃管直径的变化，其阻抗力均值变化并不明显，拟合趋势斜率仅为1.4；阻抗力峰值随直径的增大，有小幅的增长，增长线性斜率为4.36.因此，可以得出，相比压溃管壁厚和导锥角角度，压溃管直径对阻抗力的影响较小.

表4 不同直径的压溃管阻抗力对比Tab.4 Comparison on the resistance of expandable crushing pipe at different diameter

由以上压溃管直径与压溃管阻抗力的关系图及表格数据可以看到，当压溃管直径发生改变时，压溃管在撞击过程中受到的阻抗力峰值及均值的变化均不大，即压溃管直径的改变对其阻抗力峰值/均值的作用不大.但是，在实际产品应用中，由于过小的直径容易造成撞击过程中压溃管受力失稳，因此，前期直径的选取，应综合考虑空间限制尺寸、重量和成本等因素来选择合适的长径比.

4 结 论

本文通过对压溃管的数值仿真计算和实际产品的试验验证，证明了所提仿真方法的有效性，并比较了其差异点，同时，利用验证后的仿真计算方法研究了压溃管产品的结构参数对其阻抗力的影响，得到如下结论：

1)碰撞冲击仿真、静压仿真、静压试验稳态阻抗力值与数值仿真稳态阻抗力值基本一致，差异小于5%；

2)阻抗力峰值差异较大，如对单结构触发力的考核，仍需要以冲击仿真和冲击试验为指导；

3)稳态阻抗力波动振幅存在一定差异，即静压试验的振幅波动较大，而数值仿真的波动较小，其原因是数值仿真中压溃管材料的性能是完全一致的，而实际中压溃管局部材料的性能仍存在一定差异(性能不均匀).

4)当诱导面的锥角在15°～45°之间时，角度越大时，诱导面对结构变形的阻碍作用越大，从而引起撞击过程的撞击力初始峰值及其均值增大；反之，当锥角角度越小时，情况则相反.

5)当压溃管的壁厚增大时，压溃管对结构变形的阻碍作用增大，从而引起撞击过程的撞击力初始峰值及其均值增大，吸收相同能量的压缩变形行程减小，于是提高了压溃管在有限压缩行程内的总容量；反之，当压溃管的壁厚减小时，情况则相反.

6)压溃管的直径变化对其阻抗力性能的影响相对有限.虽然，压溃管直径的改变可以略微引起压溃管阻抗力的改变，但是，要通过改变直径大幅改善其性能，压溃管的直径改变将会很大，而由于受车辆间距、装配空间及压溃管自重等诸多因素的影响，不可能把压溃管尺寸设计得过大或过小，因此，通过改变压溃管整体直径来改善其性能是难以实现的.在实际应用中，可以直接根据安装空间尺寸来确定压溃管的直径，以控制和减少可变因素.

综上所述，本文的仿真和实物试验对比结果说明，本文方法可用于指导实际产品开发和设计.压溃管壁厚的变化比诱导锥面角和直径的变化对阻抗力的影响更加显著，压溃管直径的变化，对其阻抗力的影响较小.因此，在压溃管产品的实际研发中，应先根据安装空间尺寸确定压溃管直径；再通过控制变量，以壁厚作为粗筛条件进行仿真预研，确定壁厚范围；然后再根据性能需求，进一步对诱导锥面角等参数进行匹配性仿真优化和最终设计.