基于COMSOL的热压罐成型模具温度场分析

吕佳镁，马贵春，郭靖宇，岳 光，段连成，李云浩

(1.中北大学 机电工程学院，山西 太原 030051；2.莫斯科鲍曼国立技术大学 特种制造系，莫斯科 105005)

0 引 言

复合材料诞生于20世纪30年代，具有轻质高强、耐腐蚀、绝缘等优良性能，在我国的研究始于20世纪50年代末期，为满足性能高、重量轻、成本低的新时代飞行条件的要求，复合材料成型技术被广泛应用于飞机零部件制造，并逐渐应用于承力结构，复合材料用量可作为衡量飞行器先进性的重要指标[1].同时，复合材料的广泛应用促进了其成型技术的发展.其中，热压罐成型技术可用于大型复杂构件成型，且成型质量稳定，是目前最为常用的成型方法[2].模具作为复合材料构件成型的载体，其表面不同的温度值决定了复合材料不同的热收缩率与化学收缩率，并使构件内部积累应力梯度，从而发生固化变形，导致构件力学性能降低.可见，模具温度场直接决定复合材料构件的成型质量.

通过实验研究大型复合材料构件热压罐成型过程的成本较高，所以如何准确、高效地模拟模具温度场是当下的研究热点，工艺仿真模拟成为了重要支撑技术.Park等[3]建立了一种通用的二维固化模拟模型，用于快速模拟任意形状的复合材料结构.Hoon等[4]将复合材料固化的三维有限元公式编写成相应的程序用于模拟，所得结果与实验结果吻合.仿真软件方面，COMPRO，ABAQUS等软件常用于复合材料构件制造过程中变形的模拟[5-6].李艳霞、徐强等[7-8]综述了CFX，FLUENT等软件在复材构件温度场方面的应用，并对亟待解决的技术壁垒提出自己的思考.此外，研究中不断引入新的仿真模拟软件，如张晨群等[9]采用以格子玻尔兹曼法划分网格的XFLOW软件仿真模具温度场，缩短了前处理时间.李彩林[10]基于PAM-AUTOCLAVE软件平台对成型工艺进行模拟，分析了罐内温度场、流场的均匀性.

本文以用于某型飞机壁板的框架式成型模具为研究对象，利用COMSOL软件模拟其温度场分布情况，探究常见工艺参数对模具温度分布的影响情况，并对未来模具温度场的优化提出几点思考.

1 热压罐工作原理

如图1 所示，风扇驱动罐内气体流经热源升温后循环给模具加热，再循环冷水吸收罐内热量从而降温，其主要换热方式为热对流和热传导.罐内固化温度变化如图2 所示.

图1 热压罐工作原理Fig.1 Working principle of autoclave

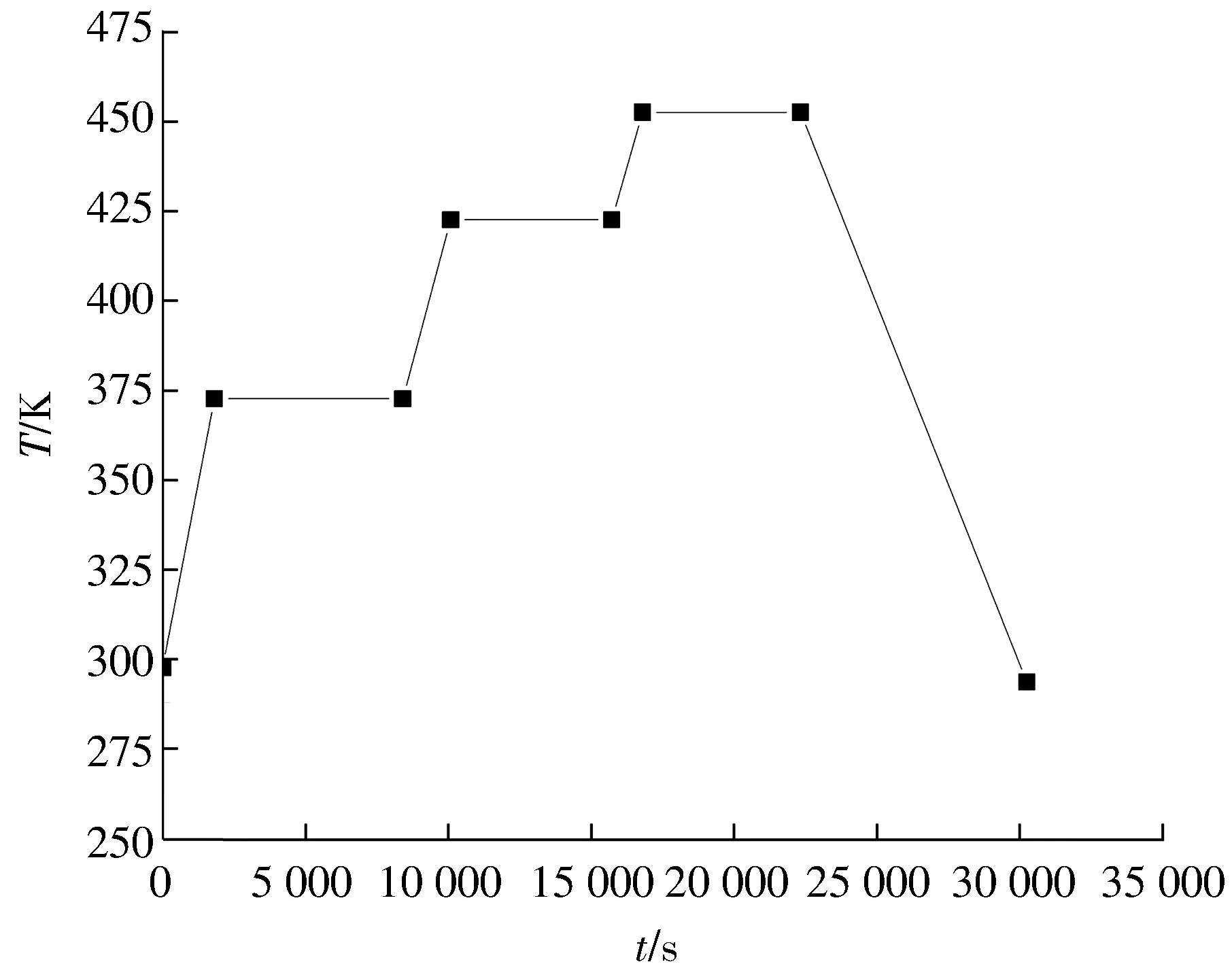
图2 固化工艺温度曲线Fig.2 Curing process temperature curve

2 数值模拟分析

2.1 COMSOL Multiphysics

目前计算流体力学(Computational Fluid Dynamics，CFD)软件颇多，各有优势.在处理高速、高精度和三维大空间等高难度问题时，对CFD软件有很高的要求.但对于工程中常见的流体问题，主流的仿真软件皆能保证计算精度.因此，在保证结果准确性的前提下，运用高效便捷、易于国人操作的工具解决实际问题是当今研究不可忽视的需求.

本文选用功能灵活的COMSOL展开研究.COMSOL Multiphysics衍生于MATLAB中的Toolbox，它与MATLAB有完整接口，非常便于后续更为深入的研究.同时，其具备完全开放的构架、友好的操作界面和语言环境，用户可对多个物理场自由耦合，根据自己的需求定义偏微分方程，再采用自适应划分网格与求解器进行准确的计算、仿真.综上，COMSOL具有良好的可扩展性和灵活性.

2.2 控制方程

2.2.1 对流传热

根据连续介质假设，罐内所发生的流体流动和传热现象均遵守牛顿力学中的三大守恒定律，即质量、动量、能量守恒，可将其作为仿真过程中的基本控制方程，在三维笛卡儿坐标系下，方程的具体表现形式如下：

1)质量守恒方程

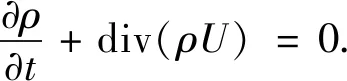
(1)

2)动量守恒(牛顿运动定律)方程

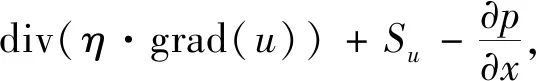
(2)

(3)

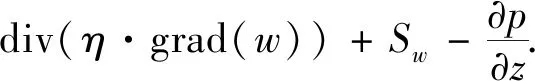
(4)

3)能量守恒(热力学第一定律)方程

-ρdiv(U)+div(λ·grad(T))+SA+φ,

(5)

式中：p为流体压力；U为流体流速；T为流体温度；ρ为流体密度；η为动力粘度；λ为流体导热率；φ为流体耗散函数；h由流体压强和流体温度决定；Su,Sv,Sw为动量方程的广义源项；SA为流体内热源；u,v,w为速度矢量在x,y,z方向上的分量.

2.2.2 传导传热

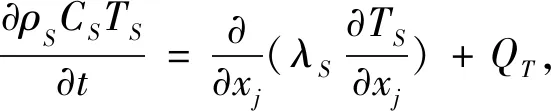
(6)

式中：ρS为Q235密度；CS为Q235比热容；TS为Q235温度；λS为Q235导热率；QT为热源项.

2.2.3 热辐射

通常情况下，在热压罐工作温度范围内，罐壁与框架式模具间的热辐射影响极弱，并且国内外有研究证明是否考虑热辐射对仿真结果影响不大，所以，本文不考虑热辐射的影响[11-12].

2.3 模型的建立

本文研究材料为Q235钢的框架式模具，尺寸为2 040 mm×1 140 mm×500 mm，型板厚度为12 mm，支撑结构为7×3的厚度为10 mm的隔板，并带有一定数量的散热孔与通风孔结构.选用工作尺寸为Φ3 mm×6 mm的热压罐，并将其简化为圆柱体结构.该模型为轴对称结构，可对一半结构进行分析以提高效率，如图3 所示.

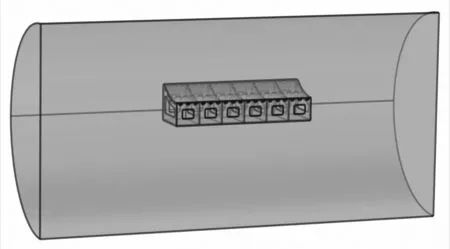
图3 成型模具简化建模Fig.3 Simplified modeling of forming die

2.4 网格划分

本文采用变密度网格.在COMSOL网格界面下选择用户控制模式，设定边界层网格拉伸因子、厚度调节因子及第一层厚度等参数，其他部分生成自由四面体网格.手动在需要细致反映数据变化处加密网格，如模具型面的过渡处等；而在数据变化平缓处疏化网格，如外部热压罐区域等.划分结果见图4.此方法可在保证计算结果准确度的基础上，减少计算成本，提高效率.

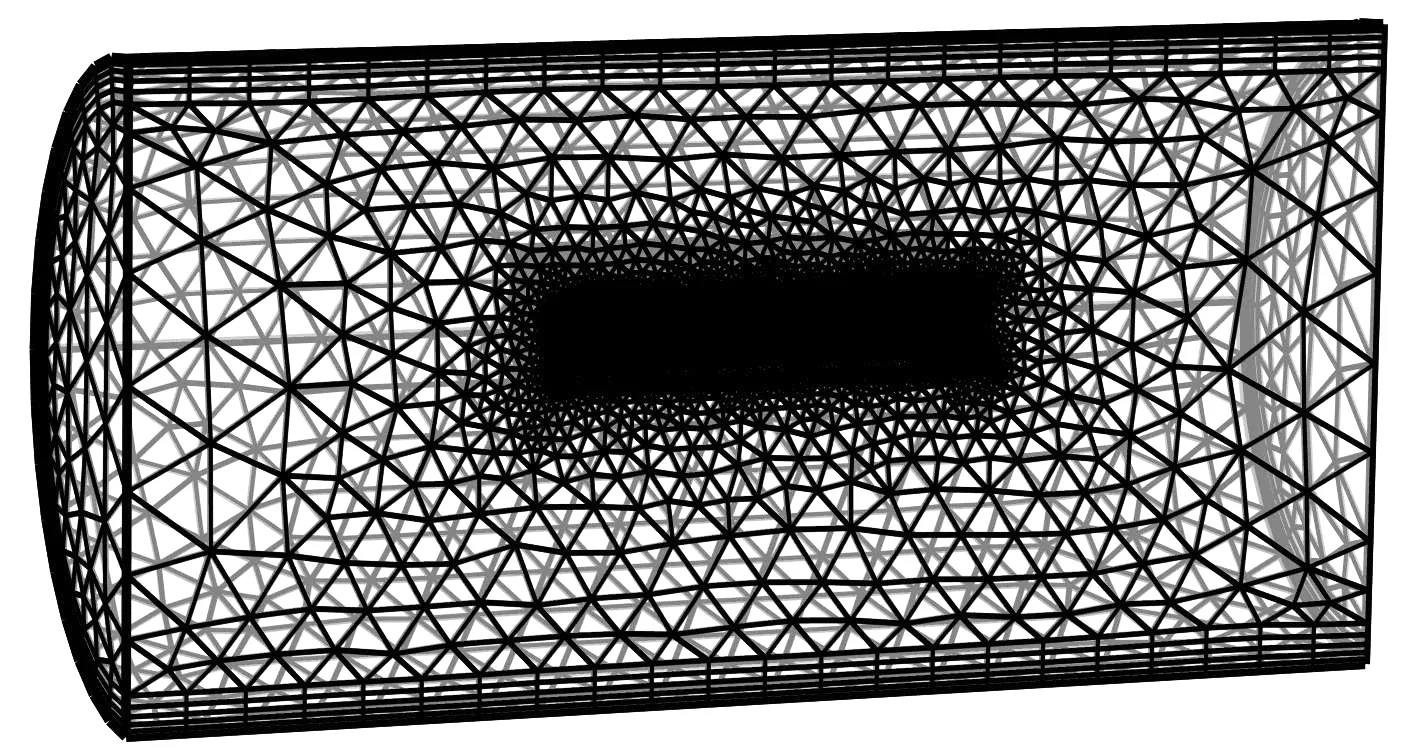
(a)整体网格划分

2.5 参数设置与边界条件

根据雷诺数所在范围，流体的流动状态可分为：

1)层流：Re≤2 300；

2)层流与湍流间：2 300≤Re≤8 000；

3)湍流：Re≥8 000～12 000.

雷诺数计算公式为

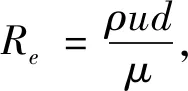
(7)

式中：u为风速；ρ为流体密度；μ为流体动力粘度；d为热压罐工作直径.

根据表1 中空气的相关参数，计算本文雷诺数Re=310 977，所以罐内流体的流动状态为湍流.

表1 材料相关参数Tab.1 Related parameters of materials

由于风扇驱动使得流体强制对流传热，在COMSOL物理场中选择湍流(k-ε)接口，流体入口速度为1.5 m/s，出口压力为罐内工作压力0.6 MPa，热压罐外壁边界设置为壁条件.又由于热压罐内共轭传热的特点，选择固体和流体传热(ht)接口，入口条件为图2所示的固化温度函数，出口为默认条件，热压罐外壁为热绝缘，中间面设置为对称.再将以上物理场耦合为非等温流动(nitf1)多物理场，设置温度条件为来自传热接口，从而实现流体与传热的双向耦合.参数设置如图5 所示.

图5 相关参数设置Fig.5 Related parameter setting

2.6 求解步骤

研究选择稳态、瞬态两个求解步骤，将稳态的求解结果作为瞬态求解的初始值，有利于计算稳定.

2.7 模拟结果及分析

1)模拟结果的准确性验证

根据参考文献[13]，仿真时在模具型面上与实验监测点对应的位置加入域点探针，如图6 所示.提取出5处具体温度值，并与实验结果比较，相关结果见表2 和表3.对比表2 和表3 数据可知，与实验值相比，各监测点温度的仿真值误差小于3%，所以模拟计算精度较高，具有可信度.

图6 监测点位置Fig.6 Location of monitoring points

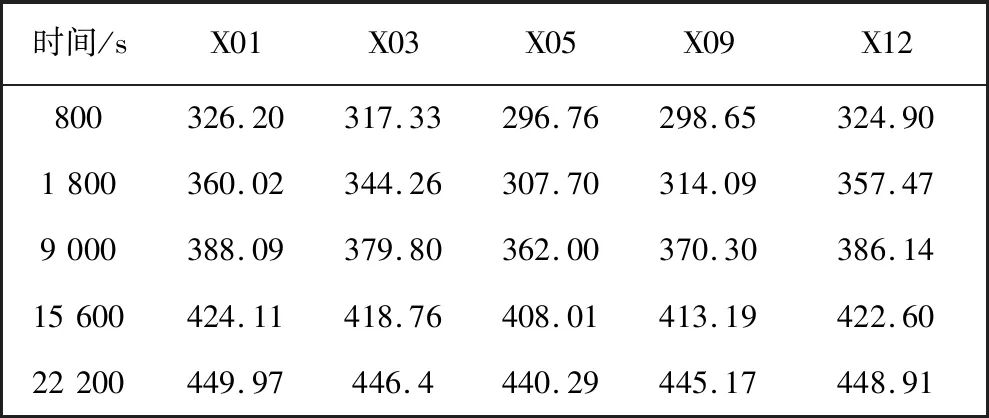
表2 仿真各监测点温度Tab.2 Monitoring simulated temperature data

表3 实验各监测点温度值Tab.3 Monitoring test temperature data

2)模拟结果的分析

图7 为模具型面在不同时间节点下的温度分布云图.从图中可以得出：在升温阶段从左端迎风区至右端背风区型面温度呈下降趋势，模具背风端中间部位存在一个低温区域；保温阶段温度分布有均匀化的趋势；降温阶段从迎风端至背风端型面温度呈上升趋势，模具背风端中间部位存在一个高温区.综上可得，模具型板中后部存在一个“温度滞后区”.该区域的温度变化滞后于型面的其他部位，从而加大模具表面温度分布的不均匀程度.

(a)t=1 800 s(第一升温阶段)

对于模具型面温度分布的仿真模拟结果可做以下几点解释：

1)流体从迎风端至背风端以强制对流的方式给模具加热，根据上文计算可知流体雷诺数较高，在流体与固体交界面处形成带有脉冲波动的湍流边界层，见图8.由于流体粘性作用损耗其动能，导致从迎风端至背风端的边界层流体速度逐渐减小，厚度逐渐增大；又因为热阻与厚度成正比，所以流体传热能力逐渐下降.

图8 模具型面边界层Fig.8 Boundary layer of mold plane

2)迎风端的支撑结构在一定程度上会阻碍流体流动并消耗能量，导致流体在背风端的冲击换热强度降低.

3)模具四周区域直接与流体接触，受外界温度变化影响大，而模具中部区域会受到四周结构的阻碍作用.

以上三点充分解释了模具“温度滞后区”的温度变化落后于其他部位的原因.

3 工艺参数对模具温度场的影响规律

本文以风速、升温和降温速率为代表探究工艺参数对模具表面温度分布的影响规律.仅分析模具型面各点温度值或温度差值难以判断整体温度分布的均匀性，而方差能够反映一组数据的波动情况，所以下文以温度方差作为模具温度分布均匀性的衡量标准[14].

3.1 流体流速对模具型面温度场的影响规律

采用第2节中的模型并保持其他工艺参数不变，分别设置流体流速为1.5 m/s，2.5 m/s，3.5 m/s，4.5 m/s，利用COMSOL得到不同流体流速下模具型面的温度分布云图，提取1 500个网格节点的温度值并计算其方差.不同流体流速下，模具型面温度方差随时间变化的趋势如图9 所示.

由图9 可知改变流体流速对模具型面温度分布有显著影响：1)相同流速下，升、降温过程中，模具型面温度方差不断增大；保温过程中，模具型面温度方差逐渐减小，温度分布逐渐趋于均匀.2)流速不同其他条件相同时，流体流速越快模具型面温度方差越小，温度分布均匀性越好，且在保温阶段不同流速的温度均匀性差异表现更明显.3)流体流速由 1.5 m/s 增大至 2.5 m/s，由 2.5 m/s 增大至3.5 m/s，由3.5 m/s增大至 4.5 m/s 的温度方差变化量分别为ΔT1，ΔT2，ΔT3，有ΔT1>ΔT2>ΔT3，由此可知，在一定范围内增大流体流速对提高模具型面温度分布的均匀性有非常明显的效果.

图9 不同流体流速下型面温度方差趋势Fig.9 The variance trend of plane temperature at different fluid velocities

3.2 升降温速率对模具型面温度场的影响规律

采用第2节中的模型并保持其他工艺参数不变，分别以升温速率u=1.5 K/min，u=2.5 K/min，u=3.5 K/min，u=4.5 K/min完成热压罐第一阶段升温过程.计算4种情况下的温度分布方差，如图10 所示.

图10 不同升温速率下型面温度方差趋势Fig.10 Comparison of temperature variance at different heating rates

采用第2节中的模型，分别以降温速率u=1.5 K/min，u=2.5 K/min，u=3.5 K/min，u=4.5 K/min从初始温度453 K降温至294 K.计算4种情况下的温度分布方差，如图11 所示.

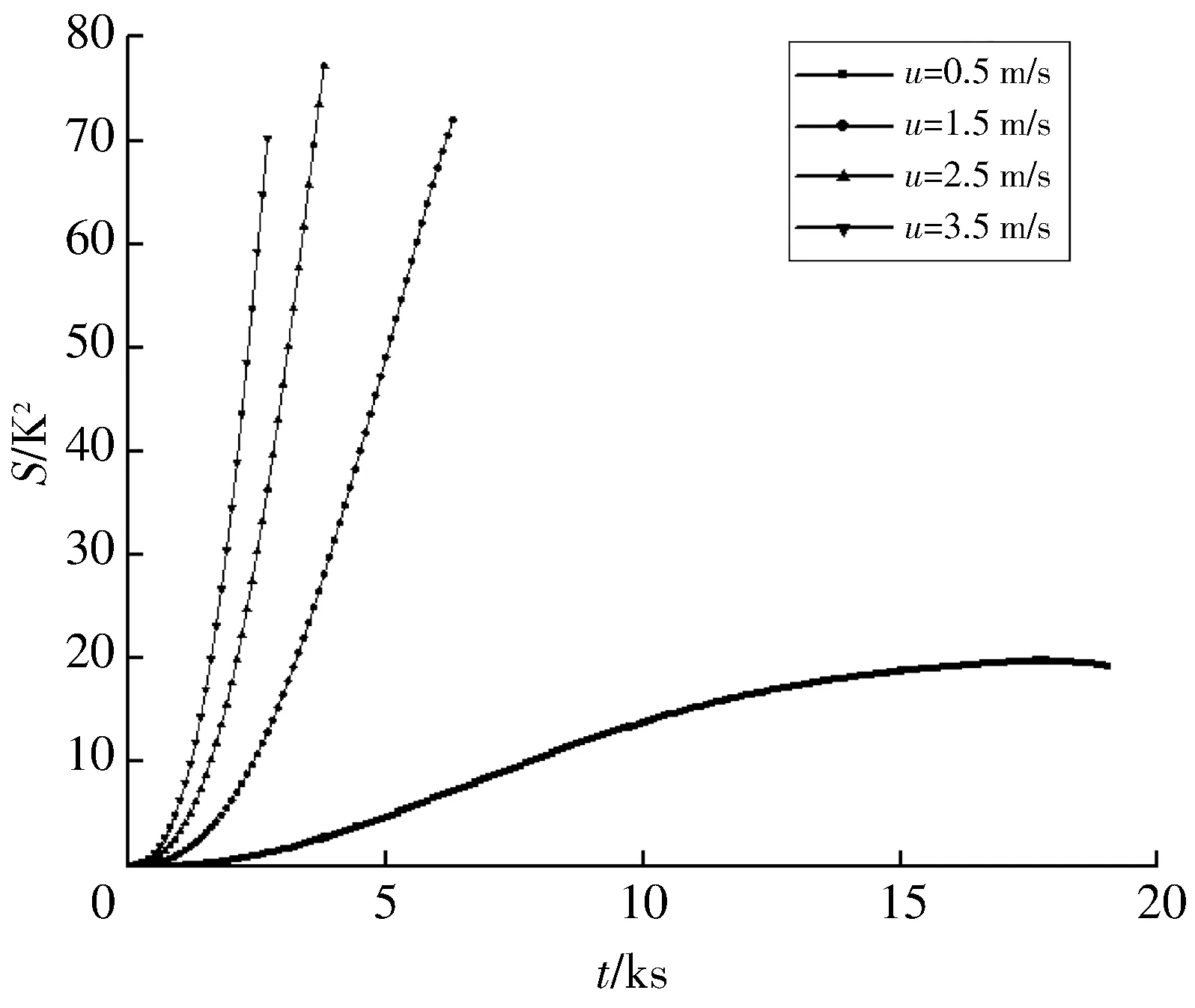
图11 不同降温速率下型面温度方差趋势Fig.11 Comparison of temperature variance at different cooling rates

由仿真结果可知，改变升、降温速率对模具型面温度分布有显著影响.升、降温速率越慢，流体与模具间换热越充分，温度方差越小.升、降温速率基数越大，增加相同数值后温度方差减小得越慢.所以，应在适当的范围内，综合考虑成本等因素减小升、降温速率将有利于提高模具温度分布的均匀性.

4 结 论

本文将COMSOL仿真引入到热压罐成型模具的温度场模拟，相关的研究思想可用于以温度为导向的多物理场耦合的工程研究中，对复合材料成型模具的优化具有一定指导意义.

1)选用COMSOL Multiphysics软件模拟模具型板温度分布情况，误差小于3%.

2)研究了流体流速、升降温速率对模具温度分布情况的影响.在适当范围内提高流体速度、考虑成本情况下减小升降温速率均可提高温度分布的均匀性.

3)模具型板背风端存在“温度滞后区”，提高此区域温度随固化工艺温度曲线的变化率，是解决模具温度分布均匀性问题的关键.

另外，还可以从以下两方面改进热压罐成型工艺：从对流传热角度出发，可以周期性改变流体流动方向以避免局部区域过热；从传导换热的角度出发，可以适当优化模具结构从而提高模具和流体间的传热能力.