基于振弦式传感器的桥梁监测系统设计及应用

田一鸣，曲立国，王尧伟，林 潇，谢黎明，杜赛赛

(1.安徽省交通规划设计研究总院股份有限公司，安徽 合肥 230041；2.安徽师范大学 物理与电子信息学院，安徽 芜湖 241002)

0 引 言

在桥梁领域，需要对结构的健康状况进行长期监测，特别是对结构内部的应变监测非常重要.桥梁的动力特性显示了桥梁寿命期间结构安全的重要性，特别是在容易发生大风或地震等自然灾害的地区，除了自然灾害荷载之外，车辆运输量的增加和车辆重量的增加还会引起动态荷载的增加[1-2].2020年初，广东虎门大桥桥面突然出现规律抖动，原因是沿着桥两边护栏连续放置的水马，改变了桥梁的气动外形，在大风的极限环境下，产生了桥梁共振现象.因此，对桥梁建成后的性能监测非常重要，同时，为了更准确地监测桥梁的变化，对应变仪校准精度的要求也越来越高[3].针对以上要求，研究人员提出了一系列监测方法，并采用了经纬仪技术、测量机器人技术和图像成像技术[4]，但是，这些方法往往无法实现连续运行以及无人值守的长期监测.振弦式传感器作为国内外广泛应用的一种非电量电测的传感器[5]，具有一个显著的优势是其电磁特性对物理和环境变化都很敏感.它通常被埋入被测物体内部或安装在被测物体表面，用于长期监测相应变量的变化.同时，振弦式传感器能够直接输出频率信号，具有抗干扰能力强、受温度影响小、抗震以及经久耐用的特点[6].因此，本文基于振弦式传感器设计了桥梁健康监测系统，详细介绍了监测系统的软硬件设计，并对监测系统的测量相对误差、稳定性和工作特性进行了测试.

1 振弦式传感器的桥梁监测系统硬件设计

1.1 振弦式传感器测频原理

振弦传感器主要测量振弦谐振频率，并通过标度变换计算压力、位移等参数.振弦传感器以钢弦振动的方式工作，弦的一端连接在薄的圆形膜片/板的中心[7].当膜片上施加压力时，膜片的变形引起弦的拉力变化，从而引起弦的本振频率的变化.通过电磁激励振动和频率计来测量弦的固有频率，这样，就可以利用弦的压力-频率特性来得到外部压力的大小.因此，应变仪不存在必须现场校准、信号漂移和长期使用耐久性差的问题，解决了应变片在长期使用中不稳定的缺点.振弦式传感器具有良好的测量特性，它的非线性度不超过0.1%，灵敏度不低过0.05%，温度误差不超过0.1%.应变片制作完成后，其钢弦具有一定的初始张力T0，因此其初始频率为F0.当安装应变计时，振动弦的张力随弦的变形而变化[8].振弦式传感器中振弦振动频率的变化量，可反映出受力的大小.因此，振弦式传感器能直接以频率信号输出，其频率大小反映待测信号的大小，其频率范围通常为400 Hz～5 000 Hz，频率信号采集电路即是实现输入信号频率的测量电路，进而反演成被测量参数的大小[9].如图1 所示，振弦传感器被扫描激振信号激振后，输出正弦信号，当输出的正弦信号赋值达到最大时，撤去激振信号，输出信号经过调整后输出频率稳定的幅值衰减正弦信号，然后经过放大电路放大信号，带通滤波器滤除干扰信号，最后通过滞回比较器整形输出方波信号，送入STM32处理器完成等精度测频.

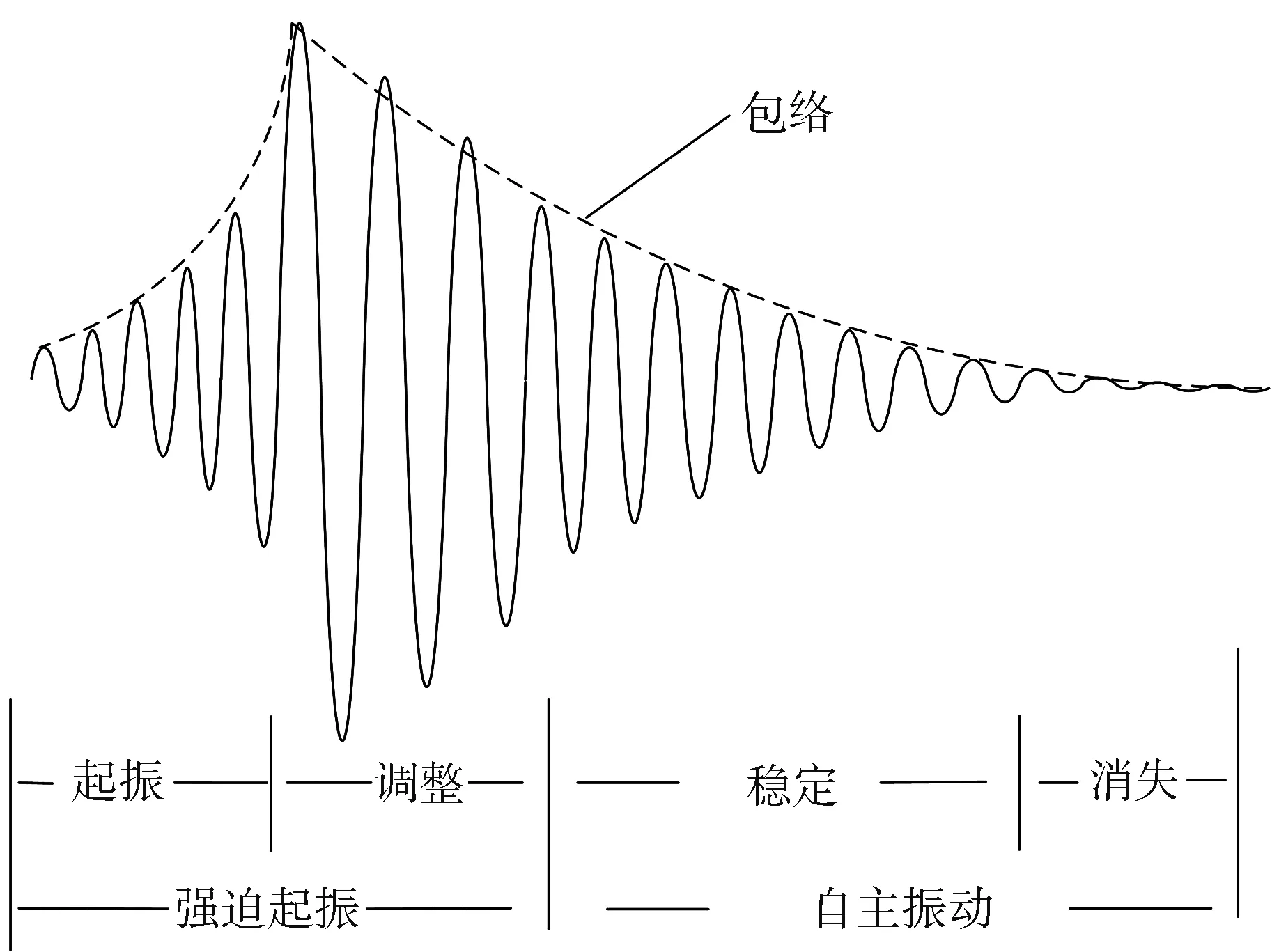
图1 振弦传感器信号Fig.1 Vibration string sensor signal

振弦传感器的信号采样方式是将正弦衰减信号通过比较器转变为方波，采用等精度测频方法测量方波频率，然后通过频率反演振弦传感器对应的物理量(位移或者压力).

1.2 监测系统硬件设计

本采集系统选用了具有丰富片内RAM资源的STM32F103系列芯片作为控制单元.硬件系统由控制器、多路选择开关、激振电路、采样电路、信号处理电路、存储显示单元和通信单元组成.在采集过程中为了对多个振弦式传感器进行信号采集，选用多路模拟开关的方式选通不同的传感器，本系统可同时测量至少8路传感器.

如图2 所示为基于振弦式传感器的桥梁监测系统硬件设计框图，系统工作后可以选通任意一路振弦式传感器，通过激振电路使传感器的钢弦起振，随即对信号进行采集，采集的信号通过信号处理电路进行滤波、整形后由STM32进行频率计算[10-11].

图2 振弦式传感器的采集仪结构图Fig.2 Structure of the acquisition instrument of vibrating string sensor

系统以ARM处理器STM32为核心，结合外部激振电路、采样电路、信号处理电路和通信电路.利用内部A/D完成模拟量信号采集，利用内部计数器、定时器和输入捕获功能完成频率信号的等精度测量，利用内部定时器输出扫频脉冲信号[12-14].激振电路采用MOSFET场效应管实现ARM处理器输出扫频信号的放大驱动.开关电路采用多路模拟开关芯片完成信号的切换和隔离.振弦式传感器输出信号经过采样电路采样后输入信号处理电路，设置二极管峰值检波电路，输出信号为振弦式传感器振荡电压信号的包络幅值，然后送入ARM处理器的A/D转换器，实现包络电压检测.放大电路采用集成运算放大器构成的二级同相比例放大器.带通滤波器由集成运算放大器构成二阶有源低通滤波器和高通滤波器并进行串联来实现，通带频率为400 Hz～5 000 Hz.

2 振弦式传感器的桥梁监测系统软件设计

2.1 主程序软件流程设计

系统采样模式可设置为周期定时采样和单次触发采样，以满足不同的采样需求，采样数据同时保存在板载的SD卡中，以便系统网络中断时自主进行离线采样.系统主程序软件流程如图3 所示，系统上电初始化后，数据采集单元随时监听来自通信网络的控制命令，当收到网络发送来的配置数据后，将其存储在采集仪的FLASH中，接着修改配置参数.然后根据设定的采样模式进行数据采样.所有通道数据转换结束后，将采样数据进行标度变换、保存.最后将数据通过网络传输模块发送到监控中心的控制服务器上做进一步处理.在进行软件设计时，需要将数据传输与数据存储两部分设置为并行运行，这样设计的好处是只要不同时发生网络传输故障和现场存储故障，系统就不会瘫痪，从而大大增加系统的稳定性.

图3 主程序软件流程Fig.3 Main program software flow

2.2 传感器扫频激振软件流程设计

传感器扫频激振软件流程如图4 所示，充分利用STM32的内部资源定时/计数器的功能实现扫频程序,由I/O口输出频率可变的信号.定时计数器工作在定时方式下，定时的时间由扫频的某一频率决定,在定时器中断程序中改变I/O口的状态,从而在I/O口检测到脉冲信号.设传感器扫频的频率上限为fmax，传感器扫频的频率下限为fmin，由I/O口输出的传感器扫频的频率fmax和传感器扫频的频率fmin之间的某一频率的脉冲个数均为N.当检测到上升沿时开始计数，并将数据存入数组，直到计数值大于N，计算频率稳定度，也就是判断数据质量，数据质量合格则完成一次频率测量.

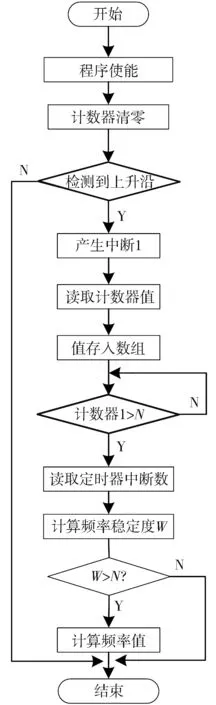
图4 传感器扫频激振软件流程Fig.4 Software flow of sensor sweep and vibration excitation

2.3 数字传感器信号采集软件流程设计

数字传感器信号采集软件流程如图5 所示，数字传感器信号采集软件主要通过设置STM32F103内部的串口与上位机通信，根据上位机指令，设置通道传感器参数(包括传感器编号、类型等)，然后设置节点地址.采用轮询访问方式配置、读取各个数字传感器输出的数据.

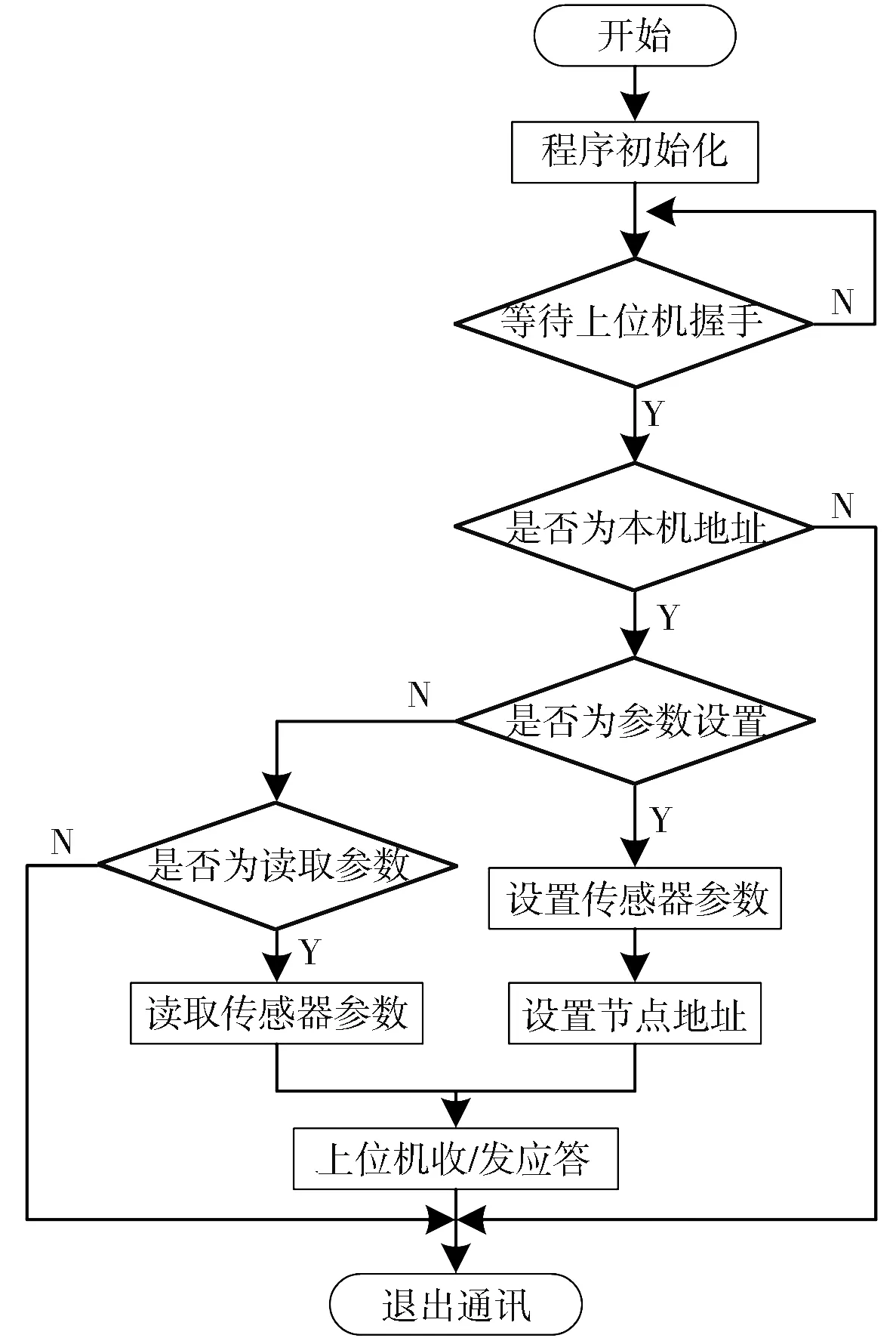
图5 数字传感器信号采集软件流程Fig.5 Digital sensor signal acquisition software flow

2.4 通信软件流程设计

如图6 所示，通信软件主要是配置下位机与上位机的通信参数，包括波特率设置、数据校验方式、通信协议设置，然后基于设定的通信协议实现系统自检、校准零点、单通道校准零点、单通道取消测量、设置定时测量参数、读取传感器编号、数据上传等功能.

图6 通信软件流程图Fig.6 Flow chart of co mmunication software

3 通信协议

在MODBUS协议下，开放三个子模块数据可读取，子模块名和子模块地址分别为测频模块(0x01)、时钟模块(0x02)、温度模块(0x03).其中，测频模块读出“频率值”2字节(单位：Hz)、时钟模块读出“年月日时分秒”7字节、温度模块输出“温度值”2字节(单位：℃).其中，测频模块写入采样方式(1字节：0x01自动采样/0x02定时采样)、定时采样时间(2字节：单位为ms)、扫频下限(2字节)、扫频上限(2字节)、扫频步进(2字节)、扫频周期(2字节)；时钟模块写入年(2字节)、月(1字节)、日(1字节)、时(1字节)、分(1字节)、秒(1字节).

在MODBUS协议下，支持基于MODBUS协议的多(单)模块读取、单个模块写入、多个模块写入三种指令，对应指令码分别为0x03，0x06，0x10.指令码的指令和返回数据帧格式分别如表1 和表2 所示.

表1 指令数据帧结构Tab.1 Instruction data frame structure

表2 返回数据帧结构Tab.2 Returns the data frame structure

例：读取地址为 0x01 的采集仪，第1个通道传感器值，子模块起始地址为 0，连续读取3个模块.

主机发送指令：0x01 0x03 0x01 0x01 0x03 0x09 0xD5；

从机返回应答：0x01 0x03 0x01 0x0B 0x27 0x10 0x07 0xD8 0x08 0x08 0x08 0x08 0x08 0x00 0xFA 0x95 0xA5，从0x27至0xFA为读取数据：频率值为1 000 Hz，时间为2008年8月8日8时8分8秒，温度值为25 ℃.

如果从机接收到非法的功能码，则无法解析并返回如表3 所示的非法功能码返回数据帧，非法功能码如表4 所示.

表3 非法功能码返回数据帧Tab.3 Illegal function code returns data frame

表4 非法功能码列表Tab.4 List of illegal function codes

4 系统测试与分析

为了验证桥梁监测传感器信号采集仪的工作特性，我们对桥梁监测传感器信号采集仪的测量相对误差、稳定性和工作特性进行测试.系统测试平台如图7 所示.

图7 系统测试平台Fig.7 System test platform

4.1 系统测量相对误差

为了验证本系统的测量的相对误差，进行了如下实验：选用振弦式位移传感器作为被测对象，同时分别用测量精度为0.02 mm的游标卡尺和本文设计的采集仪测量.改变振弦式位移传感器位移量10次，再分别用游标卡尺和采集仪测量改变位移量的大小.每次在振弦式位移传感器位置固定时用游标卡尺测量10次并取其平均值，记录游标卡尺测量平均值和采集仪测量值，如表5 所示.由表5 可知，采集仪测量值与游标卡尺最大相对误差为0.07 mm，平均相对误差为0.031 mm.

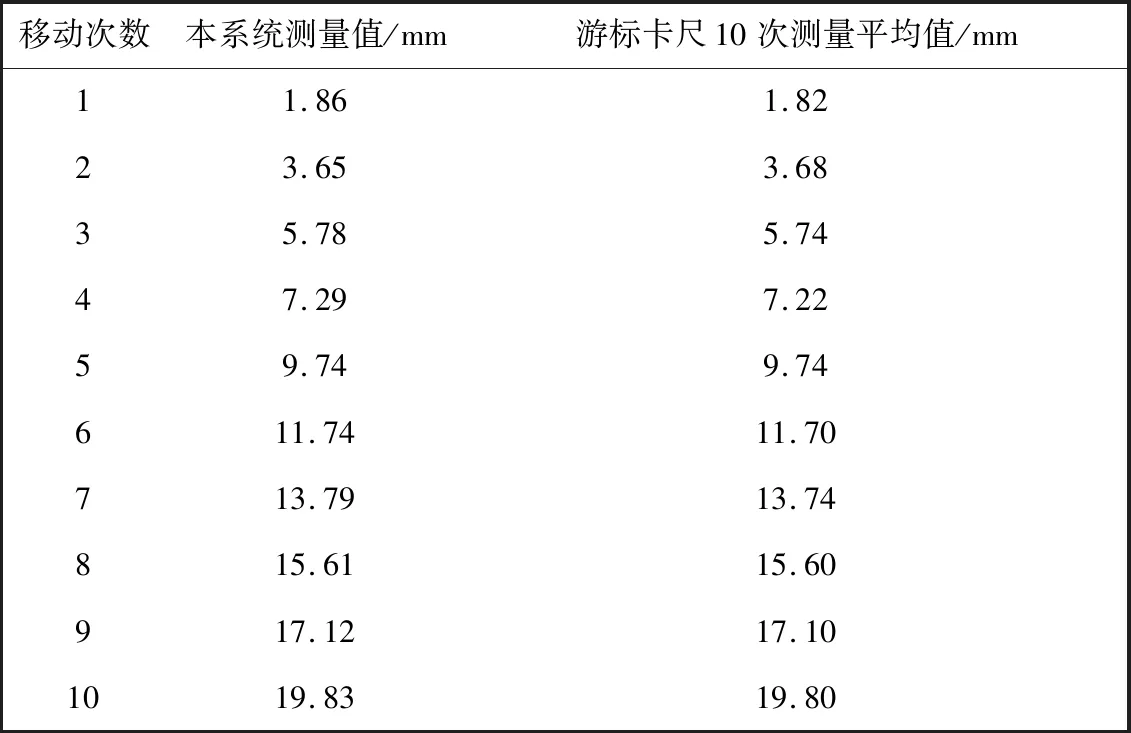
表5 测量数据Tab.5 Measurement data

4.2 系统线性度测试

为了验证本系统的工作特性是否良好，将位移传感器当前位置设置为零，然后改变传感器的位移大小，将传感器在不同位置时本系统所测的位移数据记录下来，再利用MATLAB软件对得到的数据进行拟合.先采用线性拟合方法对传感器测量的位移数据进行拟合，设直线方程y=kx+b，计算得到斜率为 0.037 42，截距为-62.075 08，也即拟合直线为y=0.037 42x-62.075 08.校正相关系数约为 0.998 49，皮尔逊相关系数约为0.999 25.

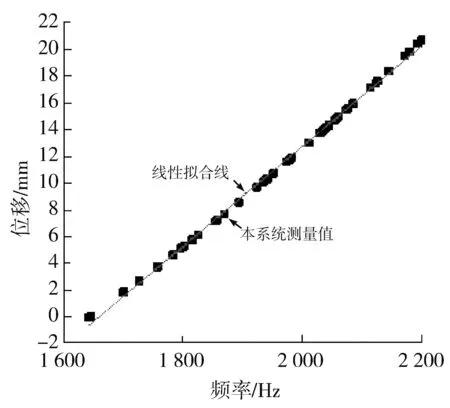
图8 线性拟合Fig.8 Linear fitting

再采用多项式拟合方法进行拟合，如图9 所示，设多项式拟合函数形式为y=Ax2+Bx+c，计算得到A1=9.674 47x10-6，B=2.193 6x10-6，C=-26.119 36，校正相关系数为1.通过这两种方法分析可以得出，本系统的工作特性趋近于直线.

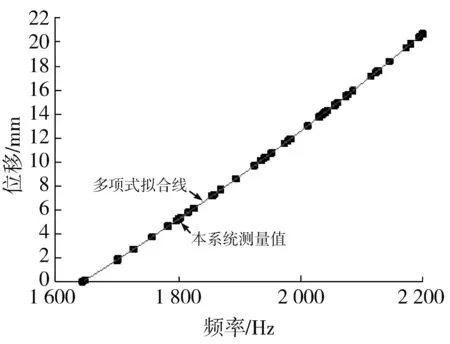
图9 多项式拟合Fig.9 Polynomial fitting

4.3 系统稳定性测试

工程上需要对桥梁状态进行长期监测，必须保证监测系统长期工作，因此，本文对所设计的监测系统进行了稳定性实验，并将分别采用市场上的上海有数电子的振弦信号采集仪与本系统所测量的数据进行了对比.图10 和图11 分别为振弦式传感器1和振弦式传感器2在静态环境(传感器处于静止状态)和相同条件下(温度、湿度、采样时间相同)由有数电子采集仪和本文设计的数据采集仪测得的频率数据.由图可以看出，本文设计的采集系统测得的数据变化小，测量的稳定度更高，其原因主要是两者所采用的测频方法不同.

图10 传感器1在不同采集仪测量的数据对比Fig.10 Comparison of data measured by sensor 1 in different acquisition instruments

图11 传感器2在不同采集仪测量的数据对比Fig.11 Comparison of data measured by sensor 2 in different acquisition instrument

5 结 论

1)本文完成了基于振弦式传感器的桥梁监测系统的软硬件设计，将STM32F103作为控制内核，可同时实时/离线监测至少8路外部传感器信号，与传统监测手段相比，本文设计的桥梁监测系统同时监测点多、采集数据量大、能够同时满足在线和离线监测，提高了采集工作效率.因此，本文设计的系统在桥梁领域及道路监测、文物保护等领域都具有广阔的应用前景.

2)本文对所设计的桥梁监测系统进行了一系列实验.测量精度测试表明，本系统测量值与游标卡尺测量值的最大相对误差为0.07 mm，平均相对误差为0.031 mm.利用安徽省合巢芜大桥作为外场实验场地，对本文所设计的监测系统线进行性度测试，结果表明，本系统采用线性拟合的校正相关系数约为0.998 49，皮尔逊相关系数约为0.999 25，采用多项式拟合的校正相关系数为1.系统稳定度测试表明，本系统长期测试数据变化小于0.7 Hz.这些实验表明，本系统具有精度高、线性度高以及稳定性强等特点，因此，具有较大的应用价值.